Controller Hardware-in-the-Loop Validation of a DSP-Controlled Grid-Tied Inverter Using Impedance and Time-Domain Approaches
Abstract
1. Introduction
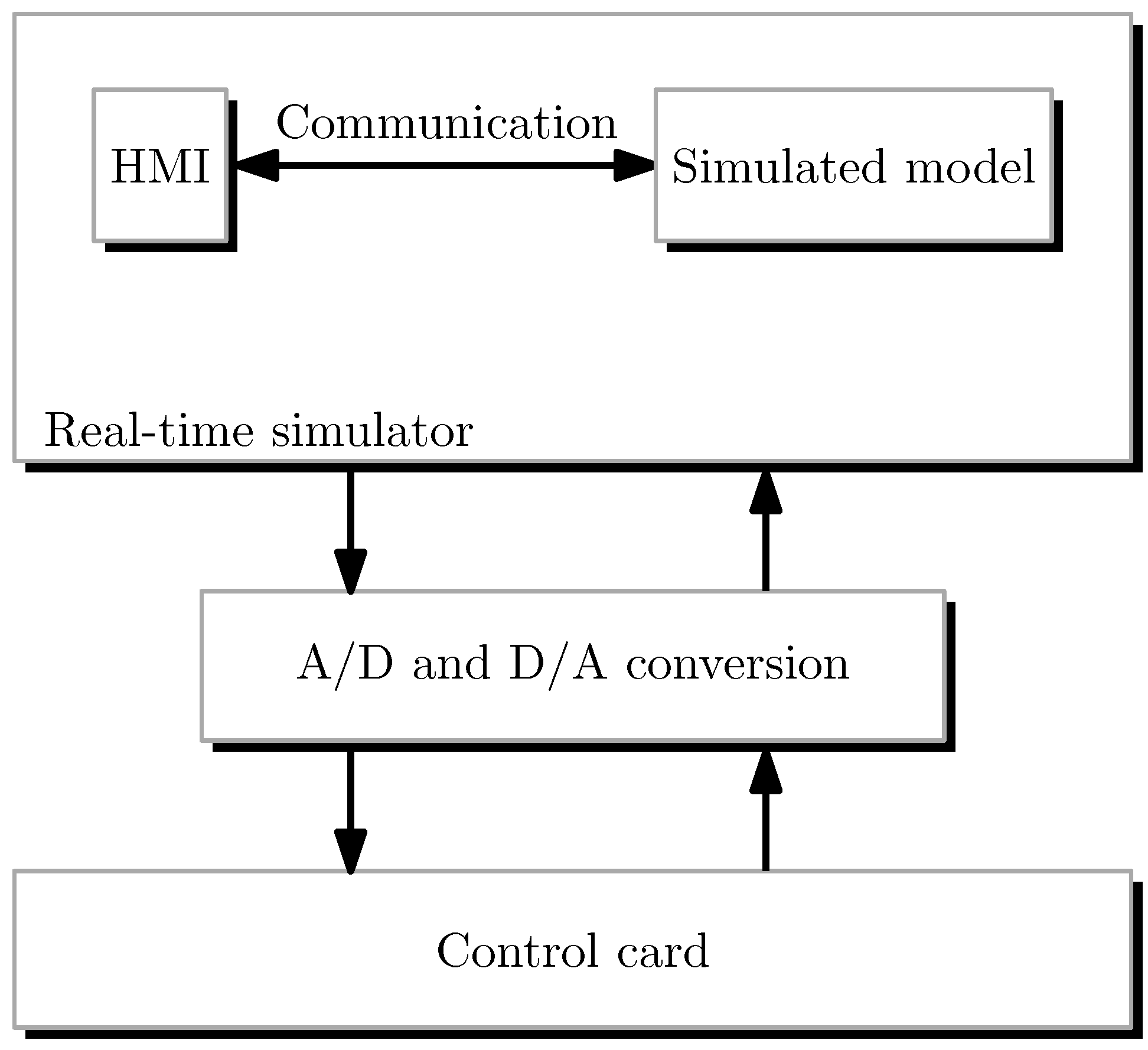
2. Introduction to Control Hardware-in-the-Loop Simulation
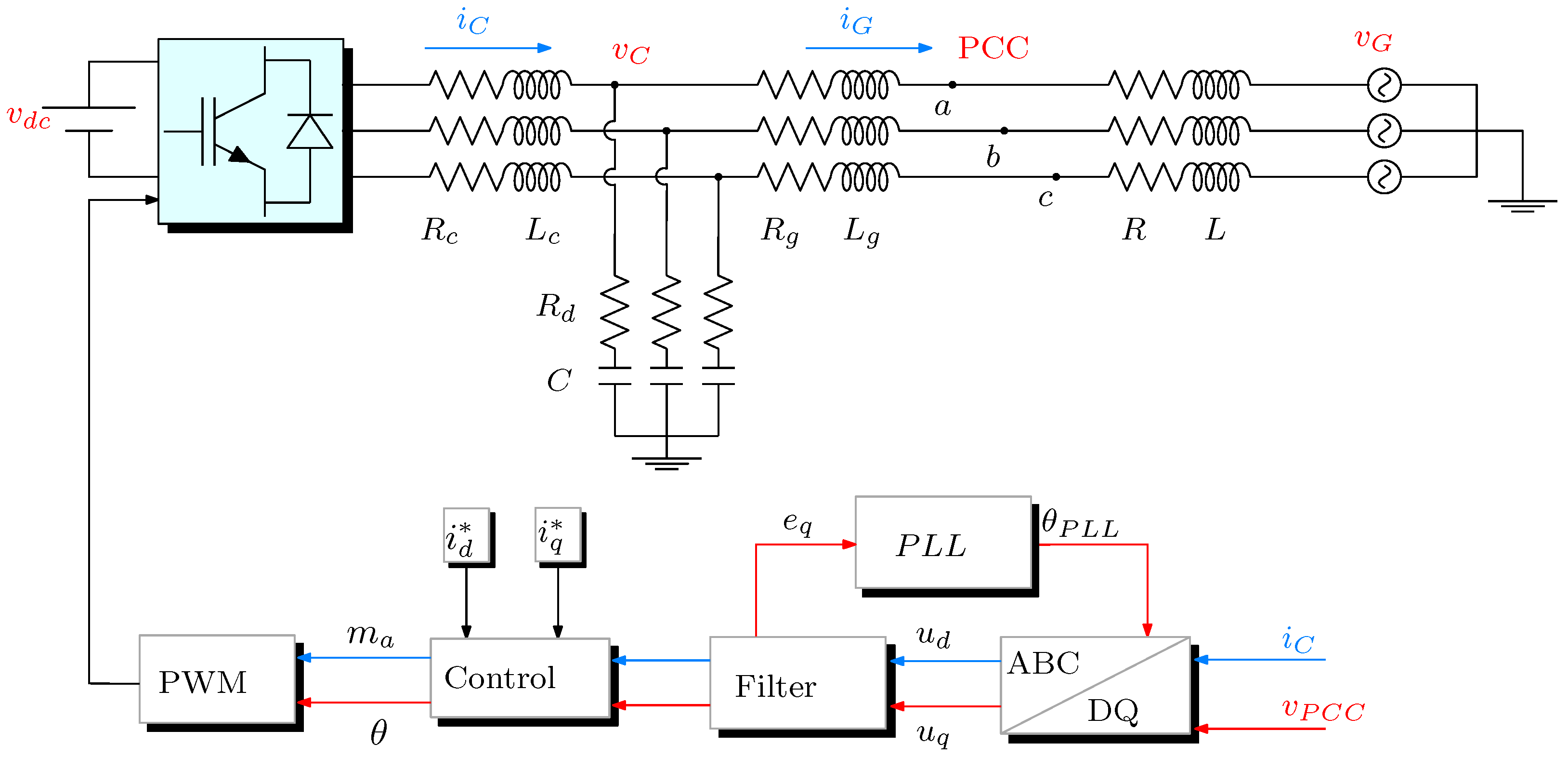
3. Modeling of Three-Phase Inverter and Control
3.1. Three-Phase Grid-Connected Inverter
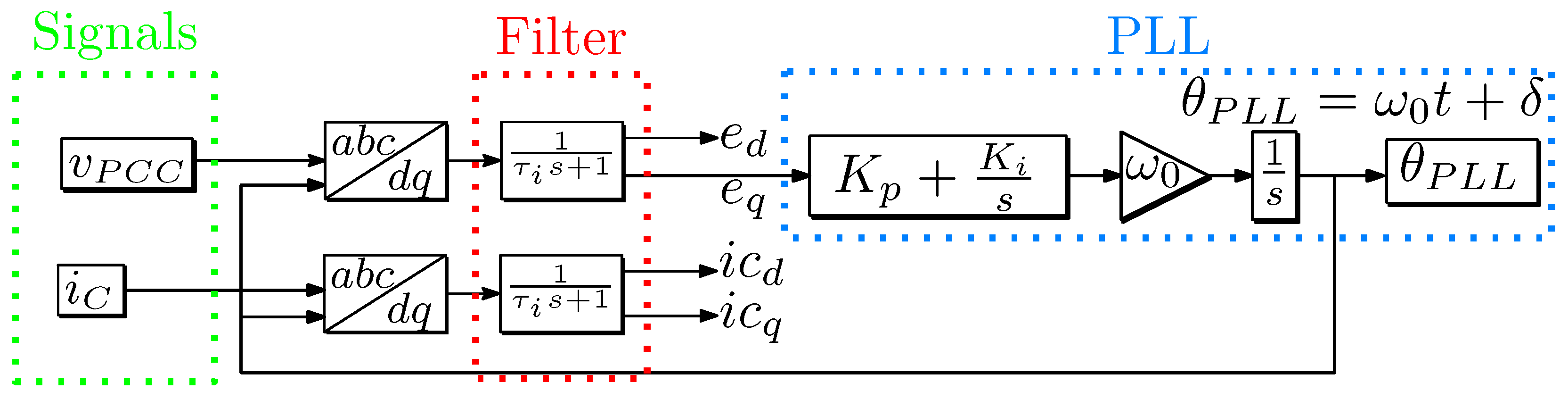
3.2. Phase-Locked Loop
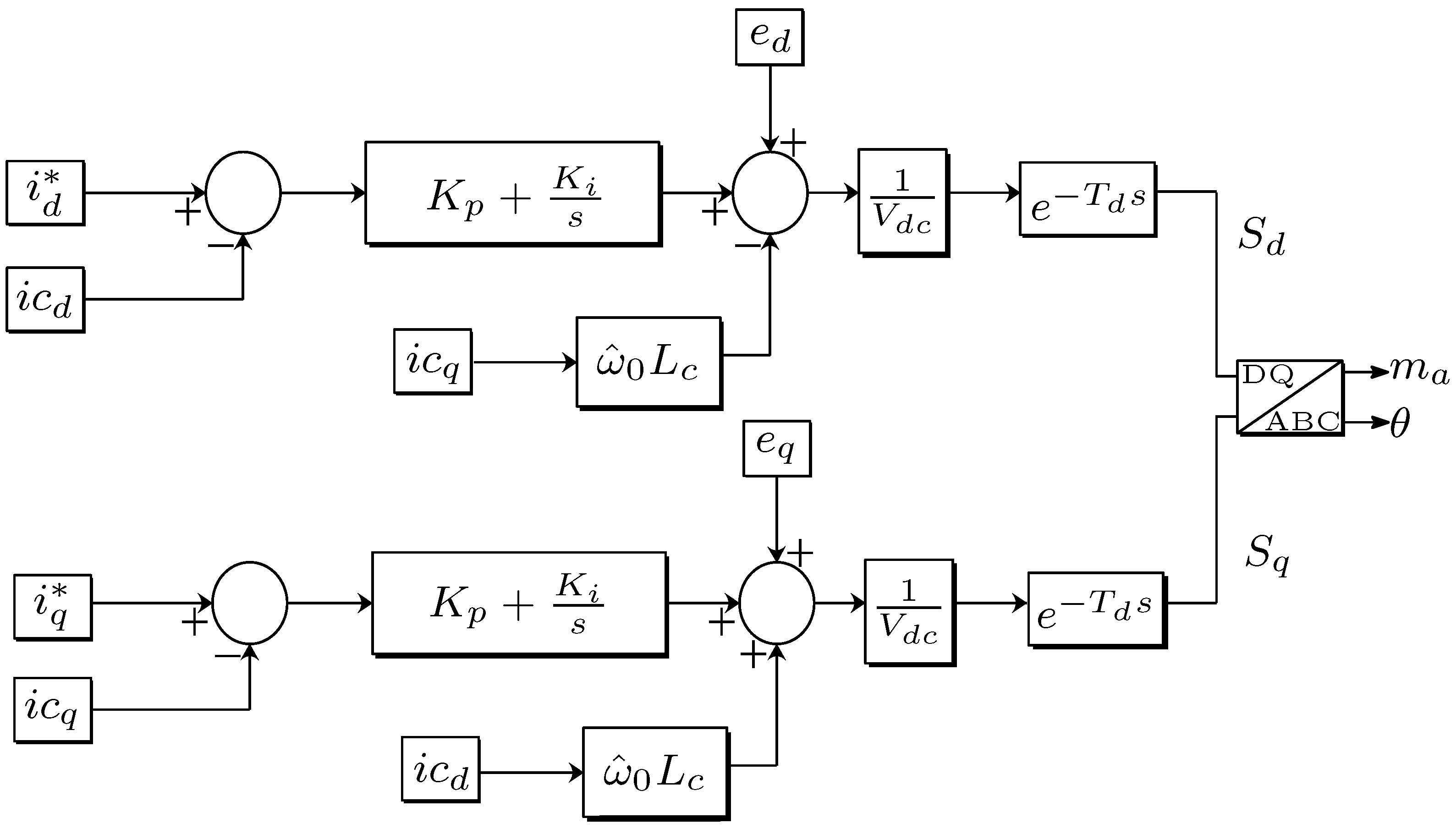
3.3. Control Scheme
3.4. PI Controller Tuning
- Phase condition for calculating is
- Module condition for calculating in requires that , i.e.,
3.5. Three-Phase Closed-Loop Inverter Model
3.6. Small-Signal Impedance Model
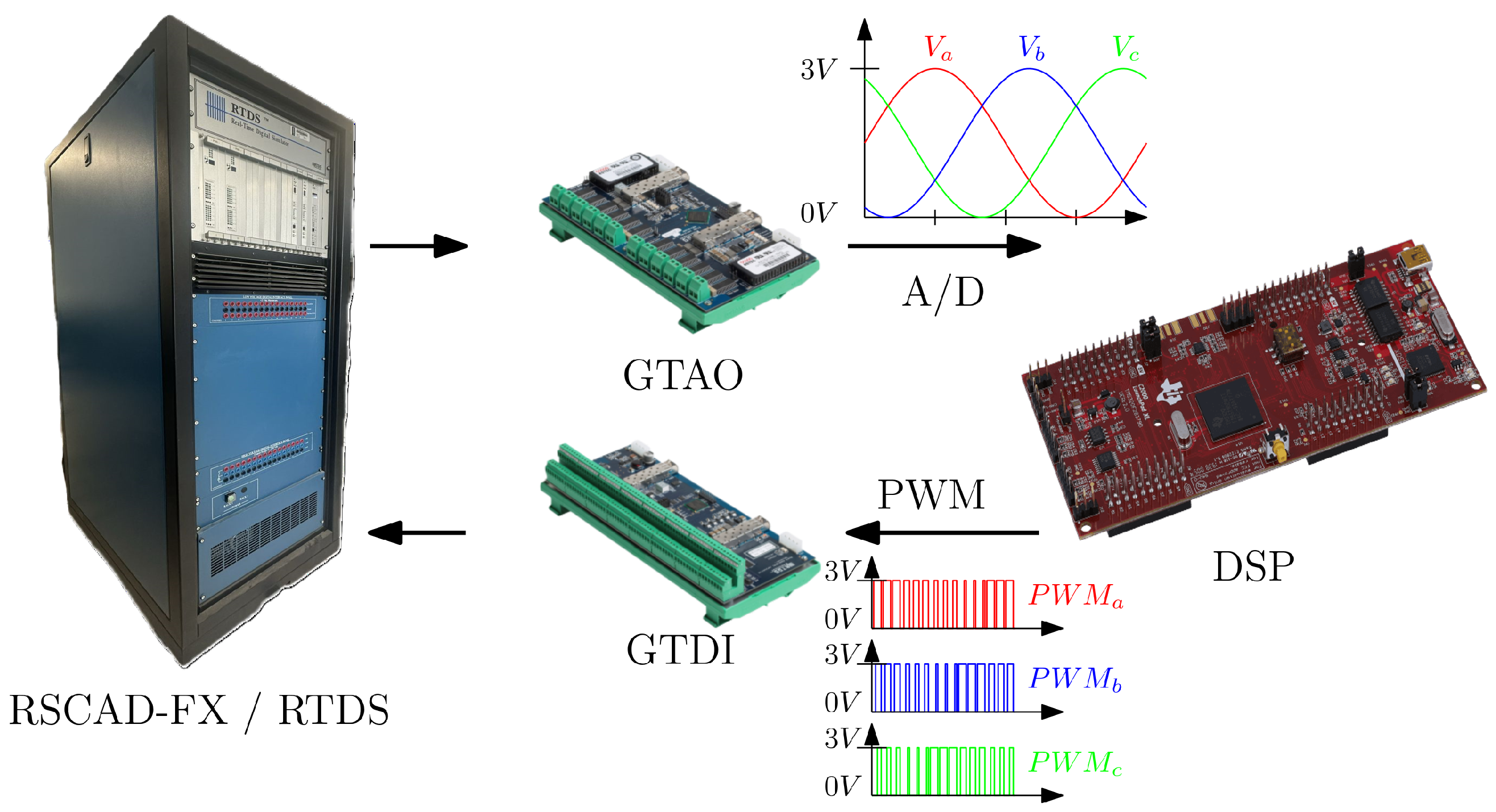
4. Insights into DSP-Based Control Integration with RTDS
4.1. Procedure
- Define the system to be controlled: Identify the system to be controlled and establish clear objectives.
- Select system components: Choose necessary elements such as the real-time simulator and data processing board.
- Configuring the simulation environment: Set up the simulator as a plant and configure all the necessary parameters.
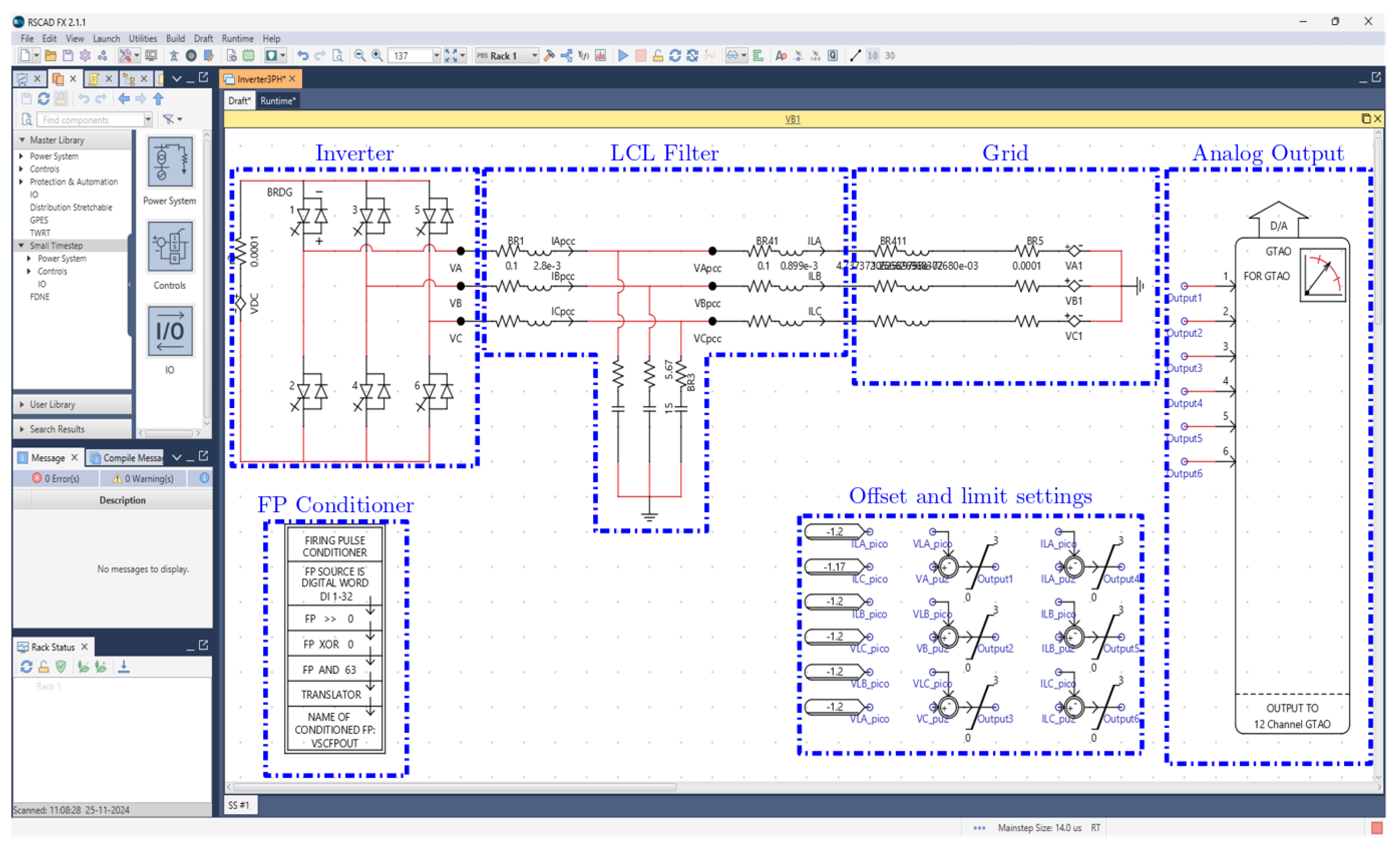
- Calibrate the inverter parameters: Adjust the three-phase inverter parameters within the simulation, including the gigabit transceiver digital output (GTAO) and the gigabit transceiver digital input (GTDI) settings.
- Integrate hardware and software: Connect DSP to RTDS, ensuring correct signal transmission.
- Perform initial tests: Perform preliminary tests to verify the correct operation and effectiveness of communication.
- Execute the CHIL simulation: Conduct simulations under different operating conditions to evaluate controller performance.
- Analyze results and adjust: Review the results obtained and make adjustments to the controller as necessary.
4.2. Timing and Digital Control Implementation
- Frequency coverage. The sampling frequency within the RTDS must be sufficiently small to capture the dynamics of the controller, i.e., if the closed-loop control bandwidth () is , the rule applies ; therefore, it is sufficient for the sampling period of the real-time simulation to be less than 1 ms [17].
- Deterministic synchrony. The DSP sampling period must be an integer multiple of the RTDS time step. This will prevent fluctuations because it ensures that each control interruption coincides exactly with a moment in the simulation [18].
- Evaluate only real-time simulation, either by implementing the control within the RTDS or by using constant values for the variables needed to construct the PWM signal that controls the power flow.
- Evaluate only the DSP, making sure that the control laws are properly executed with constant current values and verifying that the generated PWM signals are coherent.
- Connect the DSP to the RTDS, but control the system only by means of a PWM with predefined variables. This allows us to verify that the results obtained in the simulation are correct and to validate that each component is properly configured.
4.3. Methodology
- Obtaining current and voltage signals from the system: This step is crucial to ensure that the initial conditions are representative of the real system.
- Normalization and proper signal transmission to the DSP: Correct normalization ensures that the signals are correctly interpreted by the digital processor.
- Implementation of the control laws within the DSP: It is critical that the control laws are implemented accurately to maintain the desired system performance.
- Construction of PWM signals using control laws: PWM signals are essential for effective hardware control.
- Reception of PWM signals in the RTDS: Correct reception and processing in the RTDS allows for the validation of the performance of the simulated system.
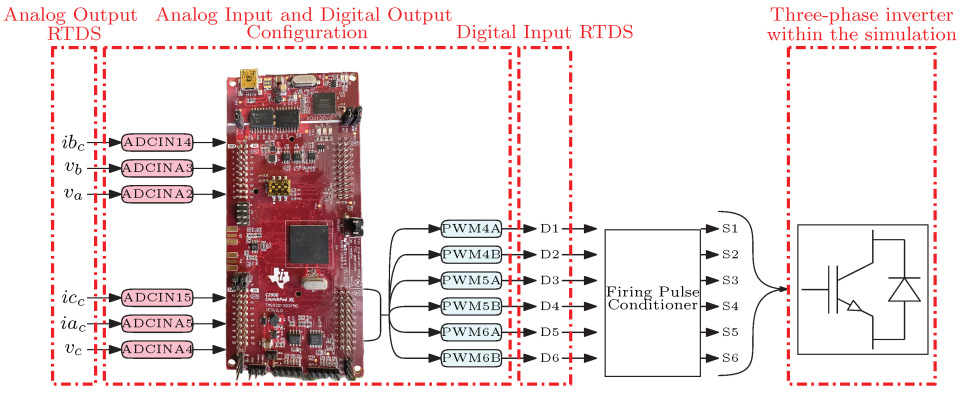
4.4. Analog I/O Path and DSP Integration
4.5. Timing and Delay Compensation
5. Results
5.1. Test Bench and Operating Conditions
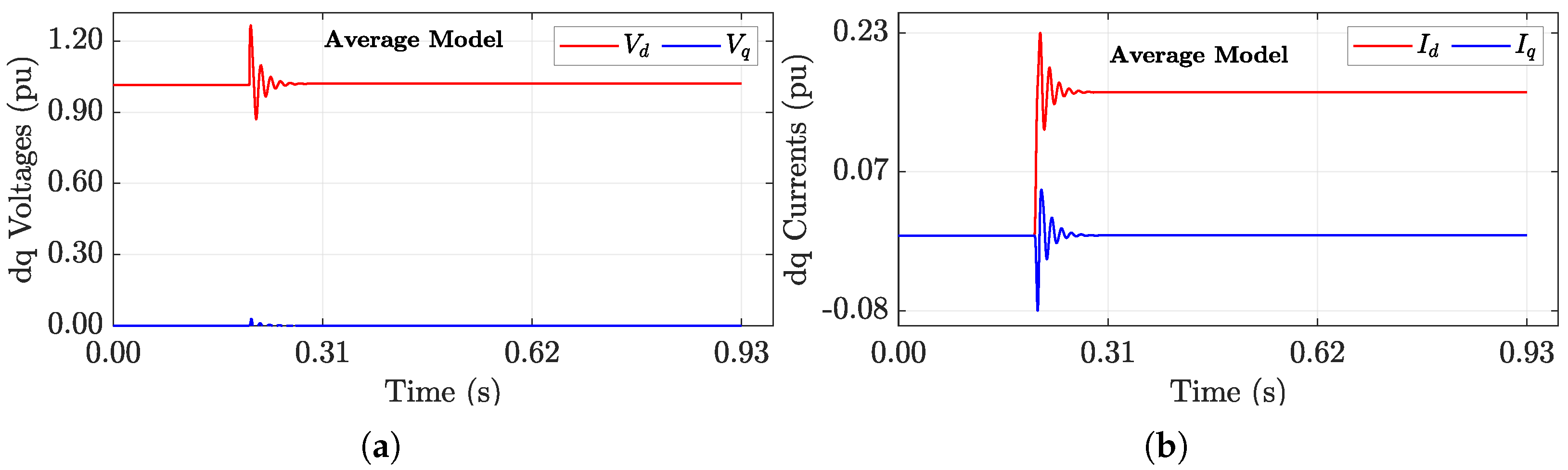
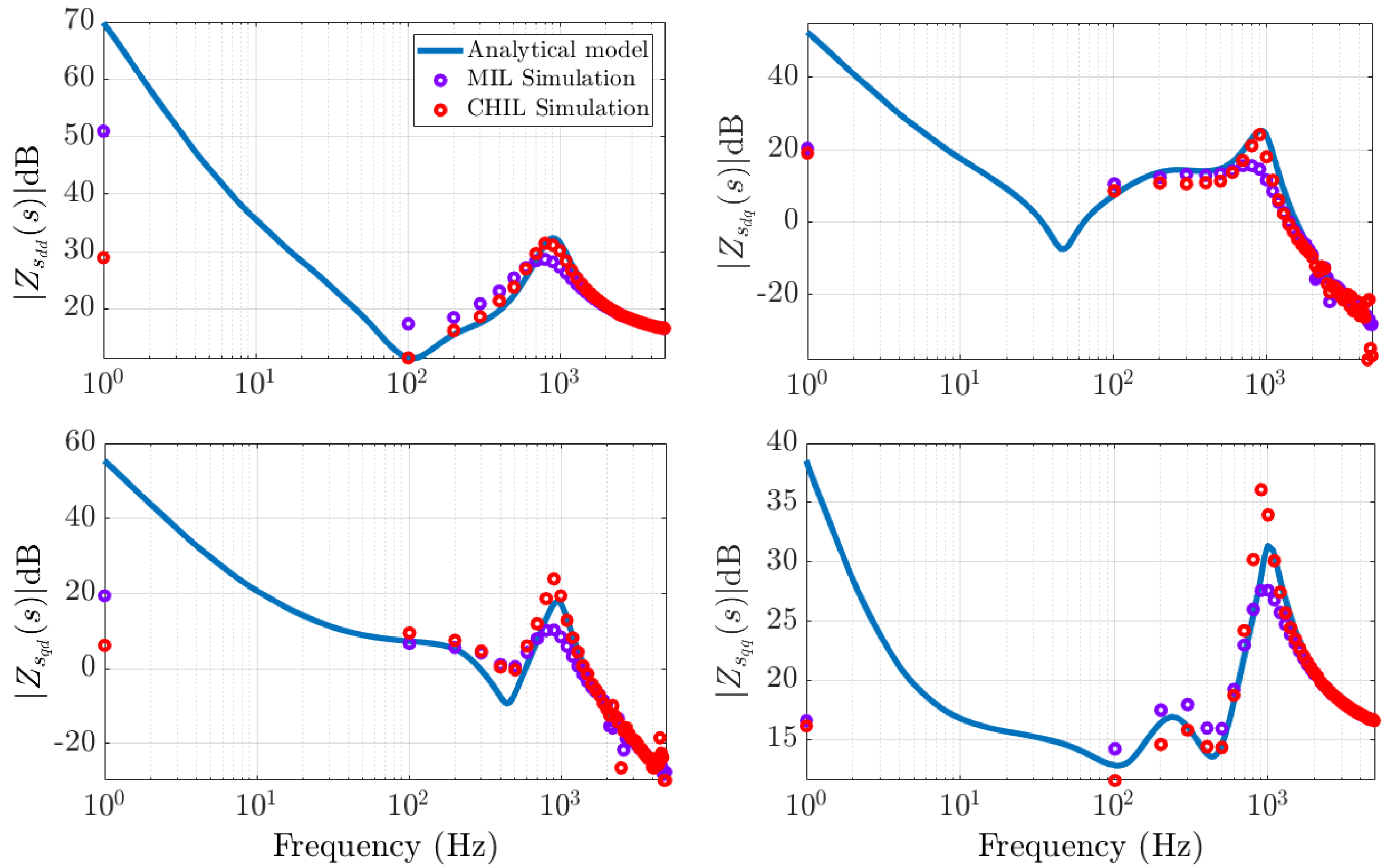
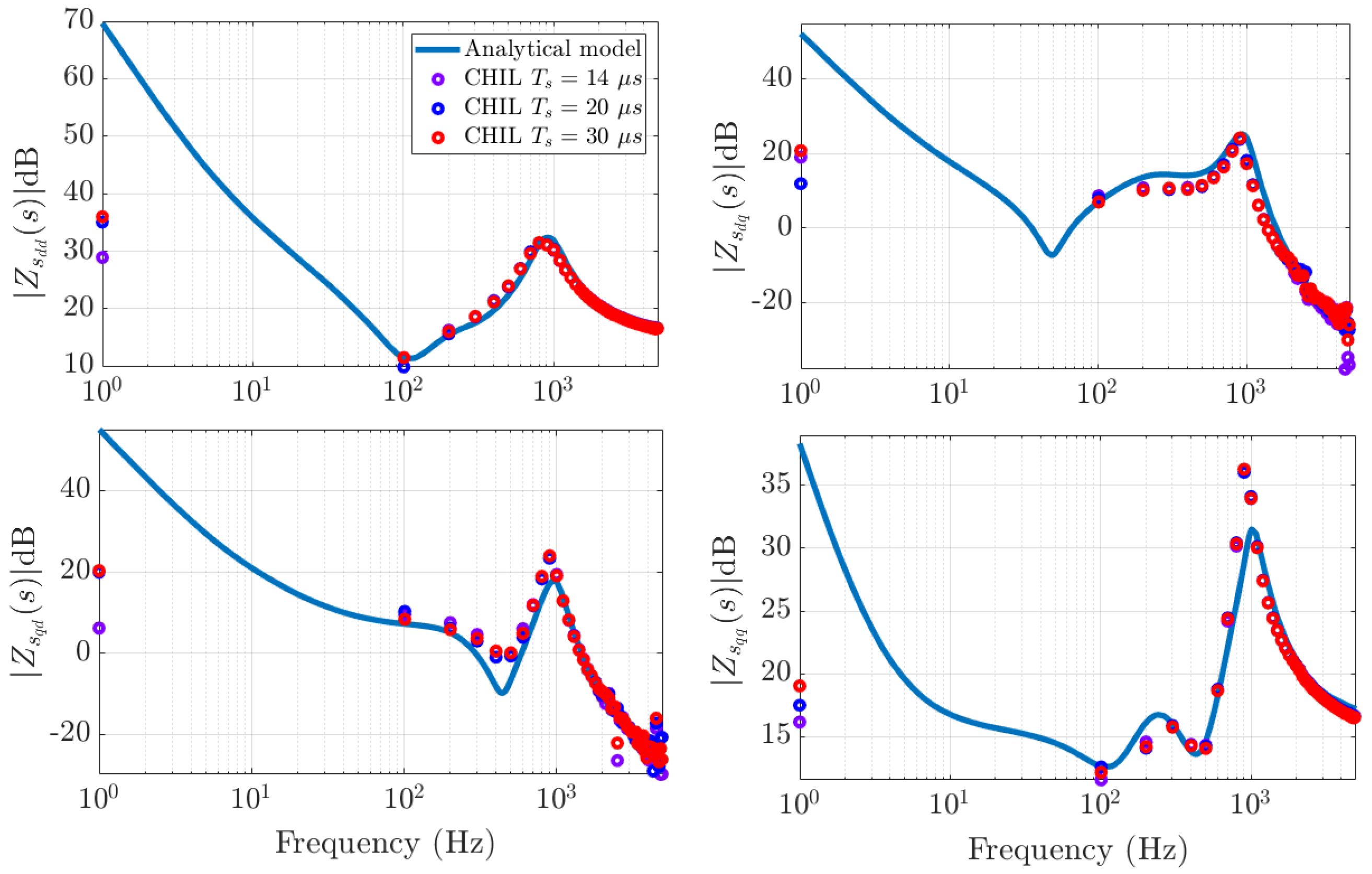
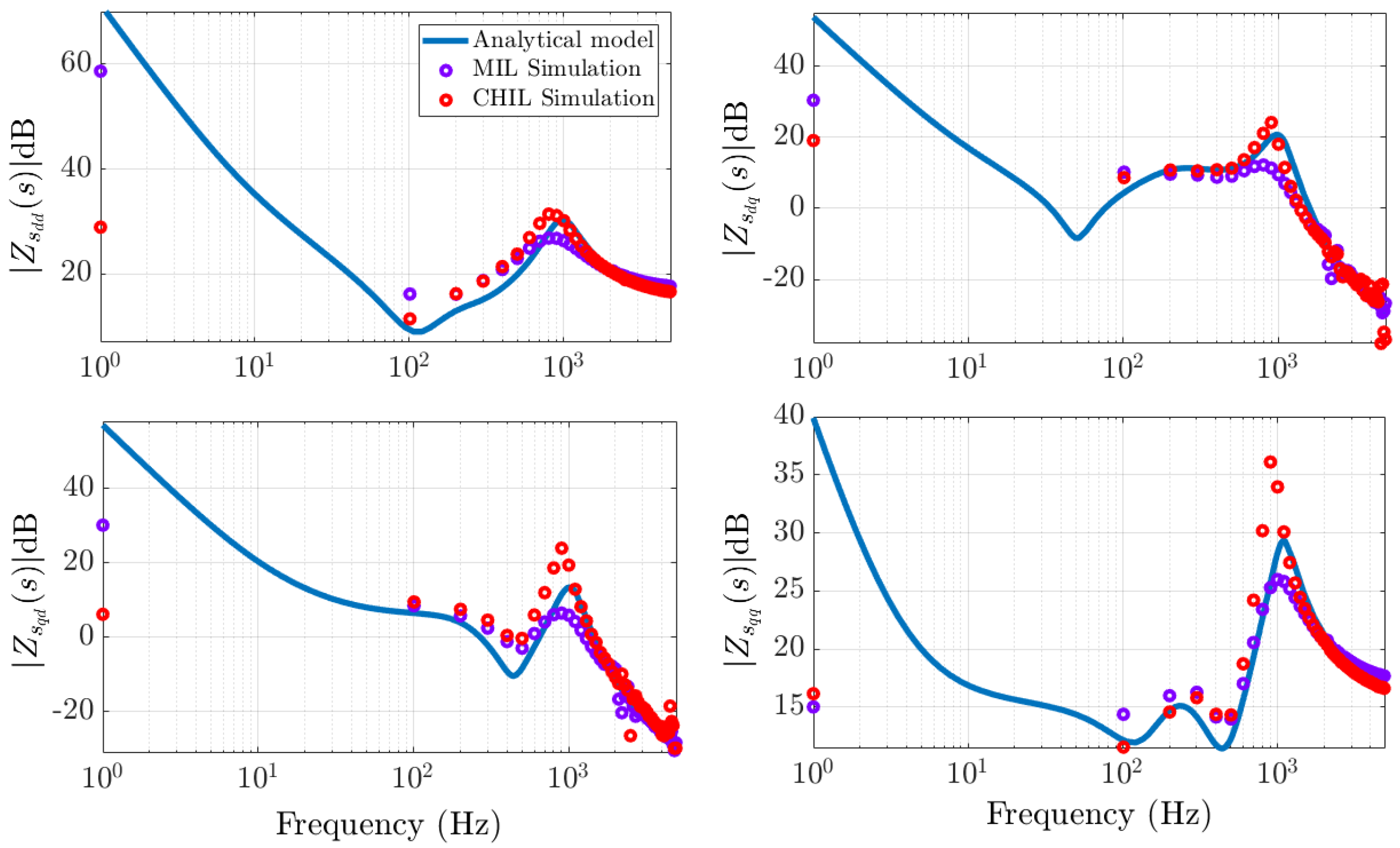
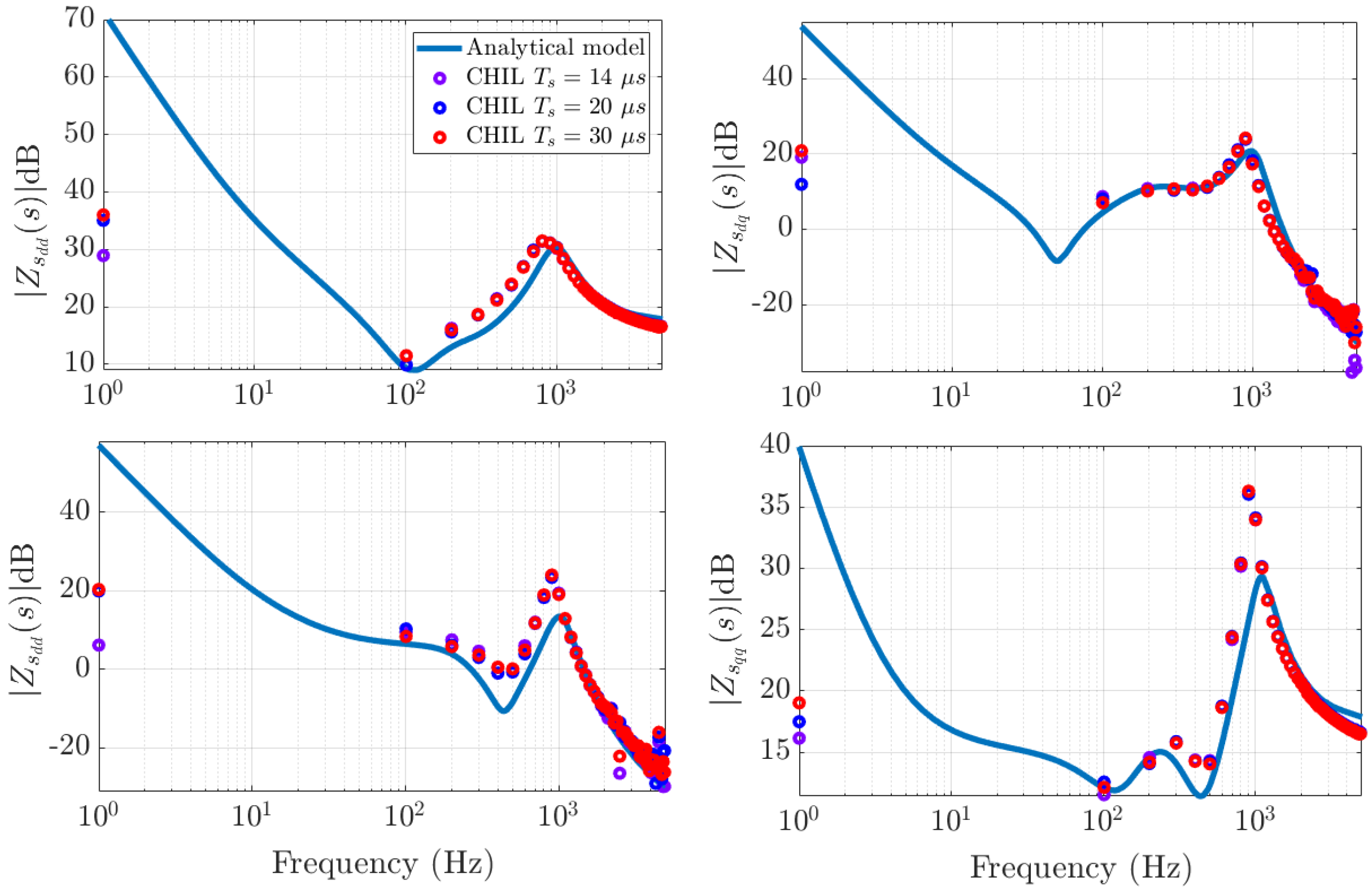
5.2. Preliminary MIL and CHIL Validation
5.3. Frequency Response Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
References
- Salas, A.B. Control Interactions in Power Systems with Multiple VSC HVDC Converters. Ph.D. Thesis, Faculty of Engineering Science, Leuven, Belgium, 2018. [Google Scholar][Green Version]
- Bashir, J.; Jena, P. Enhanced islanding detection scheme in distributed generation using phase angle analysis of negative sequence superimposed components. IEEE Trans. Ind. Electron. 2025, 1–10. [Google Scholar] [CrossRef]
- Avdiaj, E.; Lee, D.; Sakinci, Ö.C.; Beerten, J. Passivity-based design methodology for current-controlled grid-forming MMCs. IEEE J. Emerg. Sel. Top. Ind. Electron. 2025, 1–12. [Google Scholar] [CrossRef]
- Gupta, S.; Basumatary, K.; Shukla, A.; Gonzalez-Longatt, F. Real-Time Co-Simulation Platform for Grid-Forming BSS Using RTDS and FPGA. In Proceedings of the 2024 IEEE International Conference on Power System Technology (PowerCon), Kathmandu, Nepal, 4–6 November 2024; pp. 1–5. [Google Scholar]
- Basu, R.; Kuldip, C.; Kumar, M.; Lakshminarasamma, N. A Comprehensive Multi-stage Validation Approach for Development of Power Electronic Systems. In Proceedings of the 2024 IEEE 11th International Conference on E-Learning in Industrial Electronics (ICELIE), Chicago, IL, USA, 3–6 November 2024; pp. 1–5. [Google Scholar]
- Cha, S.T.; Wu, Q.; Nielsen, A.H.; ∅stergaard, J.; Park, I.K. Real-time hardware-in-the-loop (HIL) testing for power electronics controllers. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–6. [Google Scholar]
- Hidalgo Monsiváis, L.C. Three-Phase Inverter Control in Power Systems: Modeling, Simulation, and Hardware-in-the-Loop Validation. Master’s Thesis, Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico, 2024. Available online: https://ciep.ing.uaslp.mx/alumnosPos/getTesis.php?f=20994246972202.pdf&c=246972 (accessed on 9 July 2025).
- Soomro, J.B.; Chachar, F.A.; Munir, H.M.; Ahmed Ansari, J.; Zalhaf, A.S.; Alqarni, M.; Alamri, B. Efficient hardware-in-the-loop and digital control techniques for power electronics teaching. Sustainability 2022, 14, 3504. [Google Scholar] [CrossRef]
- Kim, Y.J.; Wang, J. Power hardware-in-the-loop simulation study on frequency regulation through direct load control of thermal and electrical energy storage resources. IEEE Trans. Smart Grid 2016, 9, 2786–2796. [Google Scholar] [CrossRef]
- Faruque, M.O.; Strasser, T.; Lauss, G.; Jalili-Marandi, V.; Forsyth, P.; Dufour, C.; Dinavahi, V.; Monti, A.; Kotsampopoulos, P.; Martinez, J.A.; et al. Real-time simulation technologies for power systems design, testing, and analysis. IEEE Power Energy Technol. Syst. J. 2015, 2, 63–73. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Pearson Education Limited: Harlow, UK, 2019. [Google Scholar]
- Ramírez, J.C.H. Estabilidad Armónica en Microrredes de Corriente Alterna Interconectadas a la Red. Master’s Thesis, Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico, 2017. [Google Scholar]
- Hernández-Ramírez, J.; Segundo-Ramírez, J.; Visairo, N.; Nuñez, C. Application of the Impedance-Based Method in Power Electronics: A Step-by-Step Review. In Proceedings of the 2021 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 10–12 November 2021; Volume 5, pp. 1–6. [Google Scholar]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- RTDS Technologies Inc. RTDS—Real-Time Digital Simulator; RTDS Technologies Inc.: Winnipeg, MB, Canada, 2021; Available online: https://www.rtds.com (accessed on 1 October 2024).
- Åström, K.J.; Wittenmark, B. Computer-Controlled Systems: Theory and Design; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Popovici, K.; Mosterman, P.J. Real-Time Simulation Technologies: Principles, Methodologies, and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Texas Instruments. TMS320F2837xD Dual-Core Real-Time Microcontrollers; Texas Instruments: Dallas, TX, USA, 2024; Available online: https://www.ti.com/lit/ds/symlink/tms320f28379d.pdf (accessed on 3 November 2024).
- Gu, H.; Guo, X.; Wang, D.; Wu, W. Real-time grid impedance estimation technique for grid-connected power converters. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1621–1626. [Google Scholar]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
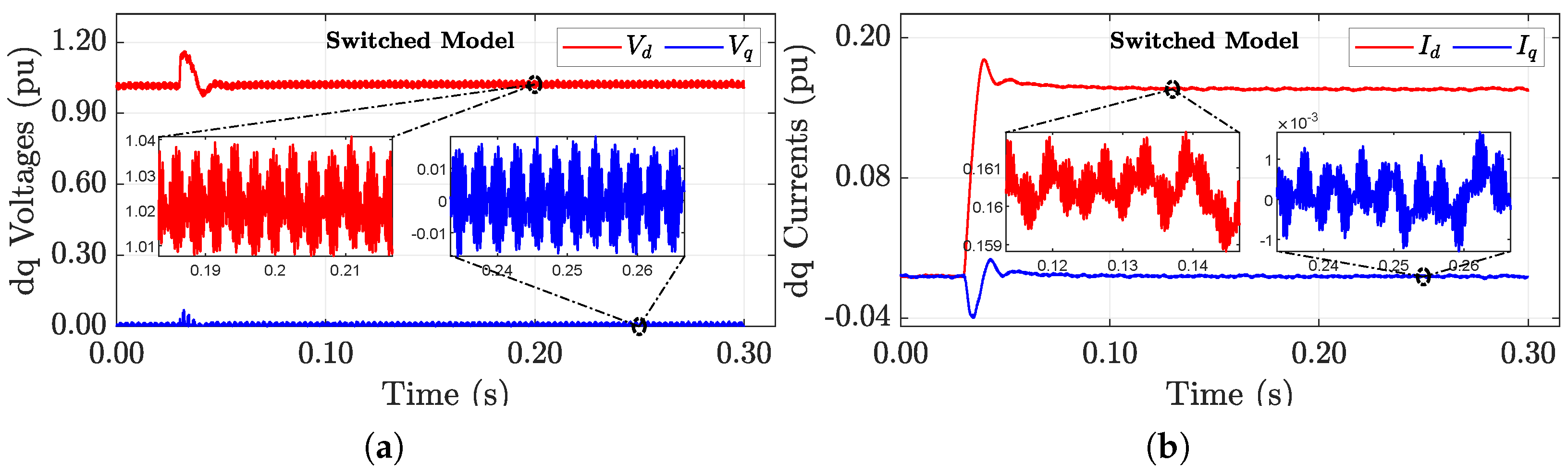
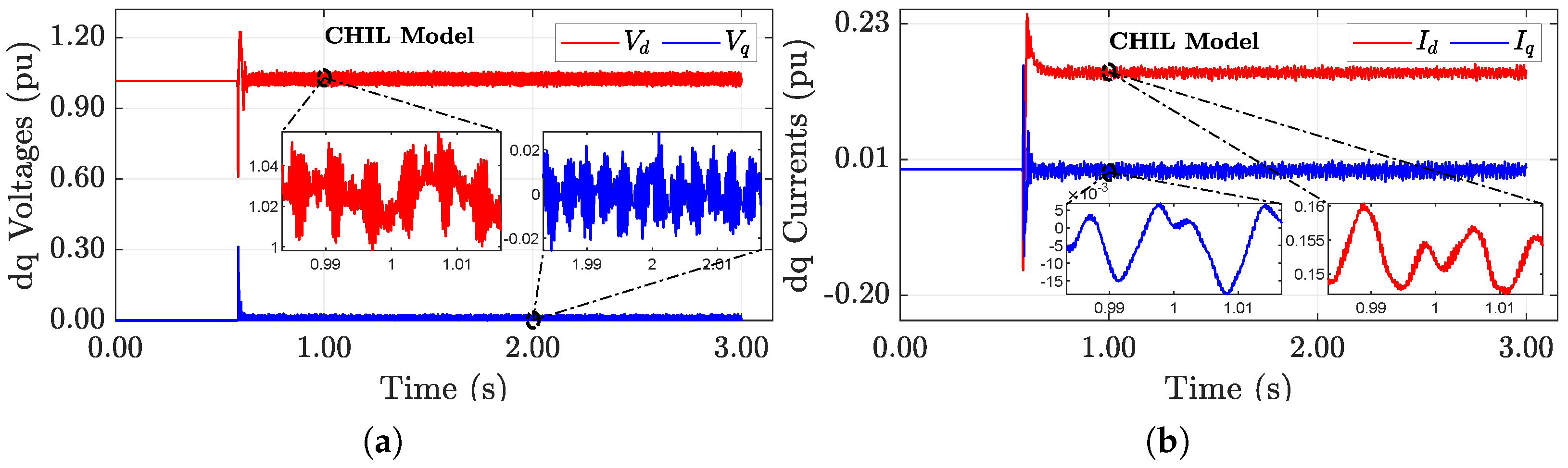
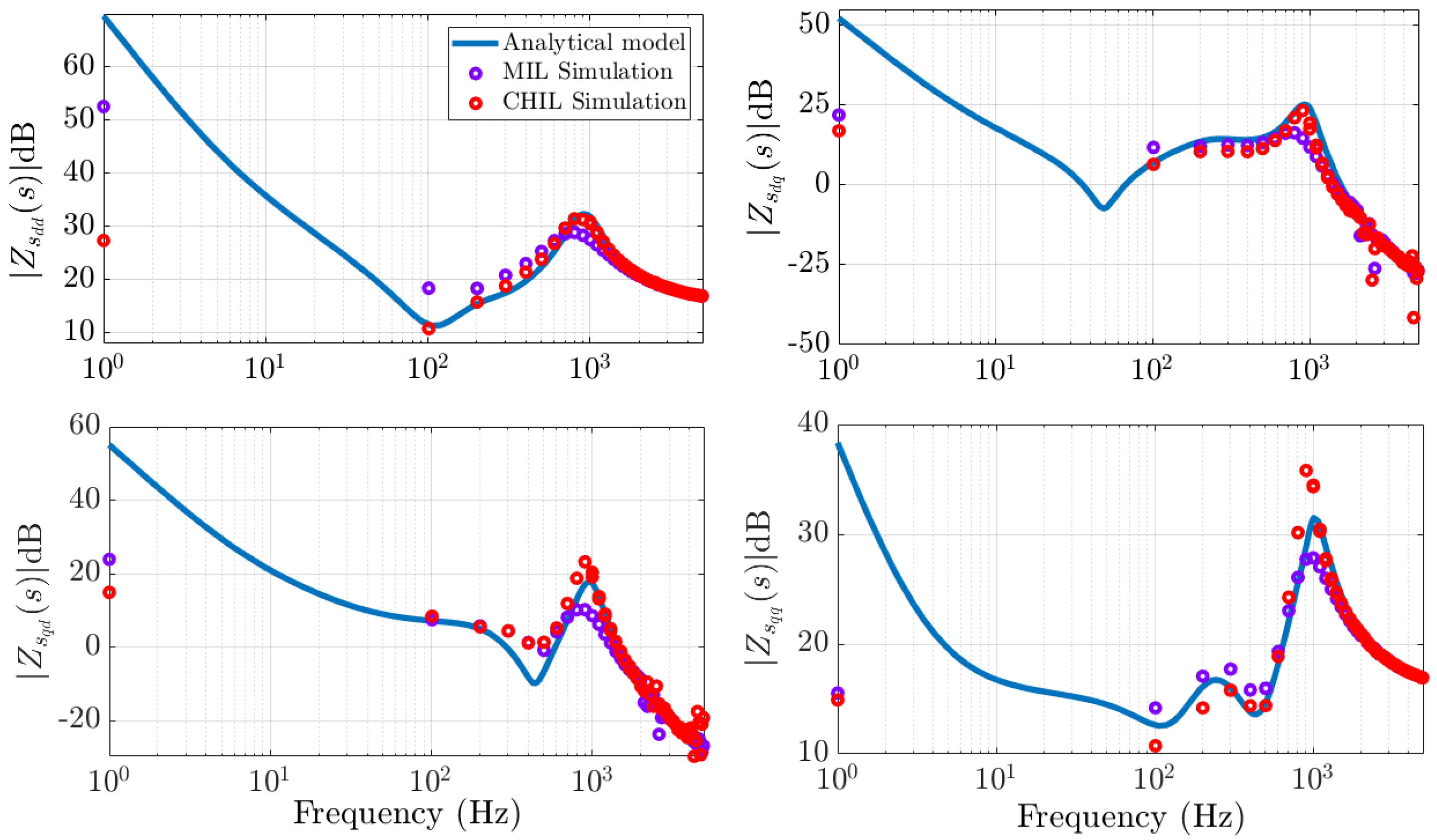
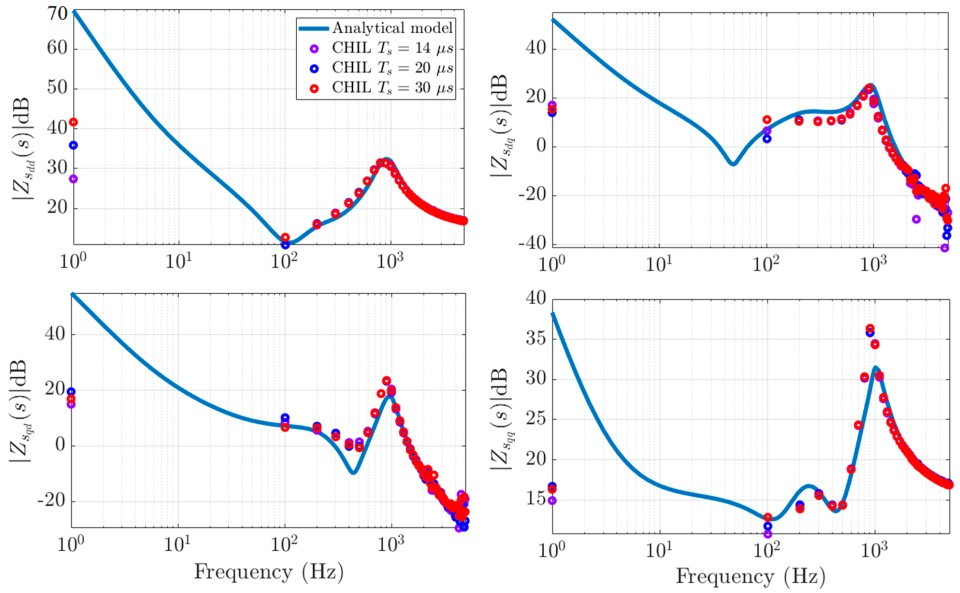
| Parameter | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| SCC | 5 MVA | 2.5 MVA | 1 MVA |
| 3.54 | 3.52 | 2.8 | |
| 2.37 | 7.93 | 2.15 | |
| 5.09 | 4.88 | 5.67 | |
| C | 13.5 F | 13.88 F | 15 F |
| 2.99 | 2.86 | 2.51 | |
| 105.22 | 110.11 | 125.08 | |
| 50 | 25 | 10 |
| Channel | RMSE MIL Simulation | RMSE CHIL Simulation |
|---|---|---|
| 1.8147 | 0.67422 | |
| 4.0676 | 4.1725 | |
| 1.1361 | 1.4164 | |
| 3.264 | 3.7677 |
| Channel | RMSE MIL Simulation | RMSE CHIL Simulation |
|---|---|---|
| 1.7644 | 0.66472 | |
| 3.8537 | 3.776 | |
| 3.1528 | 3.3321 | |
| 1.162 | 1.4195 |
| Channel | RMSE MIL Simulation | RMSE CHIL Simulation |
|---|---|---|
| 1.8432 | 1.7482 | |
| 4.1207 | 3.7659 | |
| 1.205 | 2.4042 | |
| 3.2756 | 4.764 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hidalgo Monsivais, L.C.; León Ruiz, Y.; Hernández Ramírez, J.C.; Visairo-Cruz, N.; Segundo-Ramírez, J.; Barocio, E. Controller Hardware-in-the-Loop Validation of a DSP-Controlled Grid-Tied Inverter Using Impedance and Time-Domain Approaches. Electricity 2025, 6, 52. https://doi.org/10.3390/electricity6030052
Hidalgo Monsivais LC, León Ruiz Y, Hernández Ramírez JC, Visairo-Cruz N, Segundo-Ramírez J, Barocio E. Controller Hardware-in-the-Loop Validation of a DSP-Controlled Grid-Tied Inverter Using Impedance and Time-Domain Approaches. Electricity. 2025; 6(3):52. https://doi.org/10.3390/electricity6030052
Chicago/Turabian StyleHidalgo Monsivais, Leonardo Casey, Yuniel León Ruiz, Julio Cesar Hernández Ramírez, Nancy Visairo-Cruz, Juan Segundo-Ramírez, and Emilio Barocio. 2025. "Controller Hardware-in-the-Loop Validation of a DSP-Controlled Grid-Tied Inverter Using Impedance and Time-Domain Approaches" Electricity 6, no. 3: 52. https://doi.org/10.3390/electricity6030052
APA StyleHidalgo Monsivais, L. C., León Ruiz, Y., Hernández Ramírez, J. C., Visairo-Cruz, N., Segundo-Ramírez, J., & Barocio, E. (2025). Controller Hardware-in-the-Loop Validation of a DSP-Controlled Grid-Tied Inverter Using Impedance and Time-Domain Approaches. Electricity, 6(3), 52. https://doi.org/10.3390/electricity6030052





