Abstract
This study presents a novel methodology for determining zonal electricity generation and capacity requirements corresponding to forecasted annual production in an integrated power system (IPS). The proposed model combines the statistical analysis of historical daily load patterns with a calibration technique to translate forecast total demand into zonal powers (base, semi-peak and peak). A representative reference daily electrical load graph (ELG) is selected from retrospective data using least squares criteria, and a calibration factor α = Wx/Wie scales its zonal outputs to match the forecasted annual generation Wx. The innovation lies in this combination of historical ELG identification and calibration for accurate zonal power prediction. Applying the model to Ukrainian IPS data yields high accuracy: a zonal power error below 1.02% and a generation error below 0.39%. Key contributions include explicitly stating the research questions and hypotheses, providing a schematic procedural description and discussing model limitations (e.g., treatment of renewable variability and omission of meteorological/astronomical factors). Future work is outlined to incorporate unforeseen factors (e.g., post-war demand shifts, electric vehicle adoption) into the forecasting framework.
1. Introduction
Adequate forecasting of the required volumes of electricity generation and sufficient power for integrated power systems (IPS) is crucial given the rapid development of industries and consumption volumes and the growing demands to reduce the harmful impact on the environment by reducing greenhouse gas emissions [1,2,3,4,5,6,7,8,9,10]. As the demand for electricity is also growing due to economic growth, urbanisation and the increasing electrification of industries, reliable long-term forecasting of the required parameters of integrated power systems is becoming important to ensure energy security and grid stability. Integrated power systems, which often connect several regional or national grids, require an integrated approach to accurately forecast demand, supply capabilities and potential problems.
The global trend of the rapid deployment of renewable energy sources and the growing focus on reducing carbon emissions are challenging traditional forecasting methods. The successful functioning of the IPS largely depends on balancing electricity availability and peak demand, making accurate long-term forecasting a cornerstone of strategic planning and infrastructure development in the energy sector.
Ensuring the reliable operation of integrated power systems in the context of growing energy consumption, technology development and the integration of renewable energy sources is currently a critical task. Accurate forecasting of required and sufficient power can be the basis for strategic planning, improving the efficiency of the power system and preventing energy shortages or surpluses.
Models based on regression analysis methods that take into account the dependence of power on socio-economic factors (gross domestic product (GDP), population, etc.) are presented in [11,12,13,14,15,16,17,18].
Paper [11] presents a simple model based on regression analysis that includes population and GDP per capita for the long-term forecasting of electricity demand. The model, based on energy consumption data for 1990–2012 by sector, generates projected energy demand by sector until 2025.
To predict future demand for regional energy, Ref. [12] analyses the applicable environment and forecasting conditions, performs energy forecasting for Liaoning Province from 2010 to 2019 and compares it with actual data and the elasticity coefficient. The comparison shows that the forecasting accuracy of the proposed model is higher than that of the traditional forecasting method using the elasticity coefficient, which proves the scientificity and effectiveness of the model for regional energy demand forecasting. It is argued that the method and data can provide a reliable database for the planning and development of the future power grid.
The main study in [13] is the forecasting of energy demand using Multivariate Adaptive Regression Splines (MARSs) as a non-parametric regression technique. Energy demand was modelled for the period 1975–2019 based on a combination of factors, including GDP, population, etc. Five models were created and compared with real data collected by the Ministry of Energy and Natural Resources (MENR). The third model, MARSs, was recognised as the best, demonstrating the highest predictive accuracy in forecasting energy demand.
In [14], three years of demand data and its categorical characteristics are divided into four seasons and fed into an efficient regression model called Machine Learning Categorical Boosting (ML CatBoost) to predict demand for the next year. The model uses a new gradient boosting algorithm that works efficiently with categorical features. Five different machine learning models were developed, analysed and tested to predict the hourly total electricity demand using the same data. The proposed model is compared with a long short-term memory neural network and five other ML models using performance evaluation matrices. The importance of accurate forecasting for the integration of clean energy into the grid is discussed.
Traditional demand forecasting models use linear regression, exponential smoothing, pick-up approach and other models for forecasting [15]. These models can be viewed as time series. They have a weak ability to generalise and, ultimately, demonstrate low adaptability to random changes. The proposed support vector regression (SVR) model, which is derived from machine learning, is highly adaptive to nonlinear random data changes and can adaptively account for random disturbances. The model is trained on a vector composed of historical data. Numerical results show that the SVR model significantly improves forecasting accuracy compared to traditional models.
Study [16] aims to apply a first-order model with one variable without using statistical assumptions to forecast energy demand. To improve the accuracy of forecasting, it is necessary to solve the problem arising from the collected samples, which are often based on uncertain estimates. One approach to handling these uncertain and imprecise observations is to use nonlinear interval regression analysis with neural networks to generate upper and lower bounds for individual samples. The study confirmed the high applicability of the proposed model for energy demand forecasting.
Article [17] proposes a two-stage model based on the method of least absolute reduction and selection of variables to determine the factors of energy demand. A support vector regression model with composite data and second-order exponential smoothing (SVR-CDSES) was created to forecast demand for coal, oil, natural gas and primary electricity. The results of the empirical analysis show that China’s energy demand will grow at an annual rate of 2.68% over the next decade. Demand for natural gas and primary electricity will grow rapidly, reaching a maximum annual growth rate of 8.05%, indicating an increased focus on clean energy.
Study [18] created multivariate linear regression models to estimate the expected annual heating energy demand in different building configurations and tested their accuracy. The models were modified in such a way that the complexity increased only to the point where the accuracy of the approximation remained sufficient. The result was a multivariate linear model that estimated the expected outcome for unknown descriptive variables with a relative error of 0% and a standard deviation of 1.6%.
Time series models, such as ARIMA (Auto Regressive Integrated Moving Average) and exponential smoothing [19,20,21,22], use historical data to predict future demand trends based on observed patterns. These models are particularly effective in accounting for seasonal fluctuations and short-term changes in demand.
Study [19] considers the problem of modelling the load of electricity demand. The provided actual load data were deseasonalised and the offline autoregressive moving average model (ARMA) was applied to them using Akaike’s adjusted information criterion (AICC). The obtained results show that the proposed method, based on the theory of multimodel partitioning, successfully solves the task. The developed model can be useful in studies related to forecasting electricity consumption and electricity prices.
Study [20] proposes a vector ETS (VETS) method as a suitable alternative to ARIMA for smoothing and forecasting MF time series. The accuracy of the method’s predictions was investigated using Monte Carlo simulations. The results show that the proposed method is suitable for short- and medium-term forecasting.
Study [21] proposes a method for short-term forecasting of the load on the power grid based on an improved exponential smoothing model. Based on a smoothed sequence that corresponds to an exponential trend, a grey forecasting model with an optimised baseline value is created. The inverse exponential smoothing method is used to restore the predicted values. The model takes into account the impact of factors affecting the load on the power grid. The simulation results show that the proposed algorithm has a satisfactory forecasting effect and meets the requirements of short-term load forecasting.
In [22], a multivariate forecasting method of nonlinear exponential smoothing with different weighting factors is investigated to realise short-term power output prediction. The simulations and experimental discussions show that the algorithm proposed in this paper can effectively implement power allocation compared to the traditional one.
New machine learning techniques, such as neural networks and ensemble models, offer improved accuracy by identifying complex patterns in large data sets. These models are becoming increasingly popular due to their adaptability and accuracy in dynamic CPS environments. Examples of the use of machine learning and neural networks for more accurate and adaptive electricity demand estimation are presented in [23,24,25,26,27,28,29,30,31,32].
Scenario-based forecasting takes into account different future conditions, such as policy changes or technological developments, to provide a range of supply and demand projections. This approach is particularly useful when quantitative data is limited. Approaches [33,34,35] are based on scenario modelling to account for the uncertainty of external factors (economic changes, climate impacts).
Reviews of scientific articles devoted to the development and improvement of modelling systems for energy complexes are presented in [36,37,38,39,40].
Even a brief review of the works devoted to the improvement of energy system modelling methods confirms the conclusion about the relevance of updating existing and developing new software and information tools for these purposes. Thus, papers [41,42,43,44,45,46,47,48,49,50,51,52,53,54] describe the most common modern software and information tools aimed at solving these problems.
The COHYBEM—Conceptual Hybrid Energy Model for different scales of energy potential [41]—is dedicated to bridging the gap between the theoretical foundations of hybrid renewable energy systems and their practical implementation at different scales through the new Conceptual Hybrid Energy Model (COHYBEM). The main goal is to develop a multivariate model that will allow for a new complete and comprehensive technical and economic analysis of the performance of possible hybrid renewable energy systems at different scales. The task is to determine the impact of critical parameters by changing the key variables in the developed model and analysing their consequences. The study includes big data analyses and modelling and optimisation of hybrid energy solutions that combine wind, solar and hydro power with energy storage technology in the form of a pumped storage plant. The study also shows a Pareto curve with increasing installed power.
The CYME International T&D software [42] (CYME 9.0 Rev. 4) is, from the authors’ point of view, an advanced and comprehensive world-class modelling package developed for transmission, distribution and industrial power systems. The new generation of CYME 9 software supports utilities for modernising the long-term network planning structure. It is built on the basis of such core components as time series analysis, distributed energy resource (DER) optimisation and no-wire alternatives (NWA). CYME 9.0 aims to integrate the power planning process with the distributed resource planning process. It emphasises the power and versatility of the user interface, combining simplicity with efficiency.
Power System Solutions DIgSILENT PowerFactory 2023 [43] is a software for analysing power systems: generation, transmission, distribution and industry. It covers a full range of functionality from standard functions to highly complex and advanced applications, including wind energy, distributed generation, real-time modelling and performance monitoring for system testing.
EMMA [44] is an optimisation model for the European integrated power system. It minimises the total system costs, taking into account dispatch and investments in generation, energy storage and interconnections with hourly granularity. The model includes fourteen generation technologies and two energy storage technologies. It takes into account a large number of technical constraints related to short-term system balancing, cogeneration, cyclical operation of thermal power plants and operational limitations of hydropower facilities. The demand for electricity must be met at every hour of the year, taking into account the cost of under-supply, which is EUR 1000/MWh. Border crossings are subject to net power constraints. However, the model does not include the task of discrete unit commitment and load flow calculations. EMMA is a linear programme with approximately 2 million non-zero elements and is routinely solved using CPLEX 22.1, a software package designed to solve linear and quadratic programming problems, including integer programming.
SOPS [45] is a software and information complex of the General Energy Institute of the NAS of Ukraine. The main advantages of the complex are its capabilities:
- -
- Modelling the power system as a complex hierarchical quasi-dynamic system;
- -
- Modelling a multi-node integrated power system with integer variables;
- -
- Minimising the weighted average cost of electricity generation and storage;
- -
- Long-term technological upgrading of power system components.
The complex allows for optimal selection of power units and their operating modes, ensuring the generation and redistribution of energy in accordance with the consumption schedule. The authors emphasise the versatility of SOPS, which makes it possible to explore various models of power system optimisation in a short time. The user can develop, edit, save and debug optimisation models. The connection of input data, sets, parameters, constants and variables used in the model is organised in a convenient way. You can edit parameters and input data and then run the model. The modelling results can be displayed on the model worksheets or output as separate files. Another advantage of the software and information complex [45] is the ability to conveniently compare many models, since each of the worksheets can contain its own model.
Enertile [46] is an energy system optimisation model developed at the Fraunhofer Institute for Systems and Innovation Research (Fraunhofer ISI). The model focuses on the electricity sector. Enertile is primarily used for long-term scenario studies and is specifically designed to capture the challenges and opportunities associated with the growing share of renewable energy sources. The main advantage of the model is its high technical and temporal granularity, which allows for a detailed analysis of power systems, taking into account the dynamics of technology development and RES integration.
ENTIGRIS [47] is an electricity market model designed to analyse energy systems from an economic perspective. It takes into account various factors, including market participant configurations and economic indicators, to provide insights into the development of energy systems.
TIMES [48,49] (acronym for The Integrated MARKAL-EFOM System) is an economic model generator for local, national, multi-regional or global energy systems that provides a technologically rich representation of the dynamics of energy processes over a multi-period time horizon. The model is typically used to analyse the entire energy sector but can also be used to study specific sectors such as electricity or district heating. TIMES is used to generate energy development scenarios taking into account economic, technological and resource constraints.
TIMES-Ukraine [50] is a linear optimisation model of the energy system that belongs to the MARKAL/TIMES class of models. It provides a multi-technology (bottom-up) representation of the energy system to assess energy dynamics in the long term. The Ukrainian energy system is divided into seven sectors in the model. The structure of the TIMES-Ukraine model follows the methodological approach of the State Statistics Service of Ukraine, which is aligned with the Eurostat and IEA methodology for energy statistics. More than 1.6 thousand technologies are represented in the model.
GENESYS (GENeration Evaluation SYStem) [51] is a model developed to assess the adequacy of energy supply in the Pacific Northwest region under uncertain future conditions. GENESYS is a constrained economic dispatch model that uses the Monte Carlo method to assess the effects of uncertainty. GENESYS is used for analysing the adequacy of energy supply, modelling the impact of uncertainties in generation and demand.
ARTEMiS [52] is designed for real-time modelling of power systems and power electronics. ARTEMiS provides advanced solvers and algorithms to ensure reliable, accurate computations with fixed time steps, which is essential for real-time simulations. In addition, ARTEMiS uses an advanced decomposition method that does not introduce artificial delays, which is important when modelling large-scale power grids.
LIBEMOD [53] is a multi-country energy equilibrium model based on a set of competitive markets for eight energy commodities: electricity, natural gas, oil, coking coal, lignite, steam coal, biofuels and biomass. All energy commodities are produced and consumed in each of the model countries: EU27, Iceland, Norway and Switzerland.
PowerGAMA [54] optimises generation dispatch, i.e., the power produced by all generators in the power system, based on marginal costs for each time step over a certain period, e.g., one year. It takes into account the variable power available for solar, hydro and wind generators, as well as demand variability.
The problems of existing methods are as follows:
- Most of the models are designed to assess and forecast the economic and technological parameters of the elements of the IPS and are aimed at solving the problems of minimising the current and total costs of operation. At the same time, the issues of the sustainability of the IPS and ensuring the necessary volumes of energy consumption are considered secondary factors affecting the minimisation of these costs and the payback period of capital investments.
- Other models focus on the problems of step-by-step (daily, hourly, minute-by-minute, etc.) functioning of the energy system or its elements in the presence of external influences.
Thus, the problem of determining the generalised parameters of the IPS, which determine the necessary stability of the system, which is determined by the values of the projected volumes of consumption and, therefore, generation, fades into the background.
This paper proposes a methodology and a mathematical model for determining the necessary and sufficient powers in integrated power systems according to their forecast volumes of electricity production, which are aimed at solving specific problems that arise in the process of assessing the current state and quality of scenarios for the development of integrated energy systems.
The need to develop a comprehensive methodology and mathematical model is becoming an urgent task for the integrated power systems of Ukraine and the world.
Hypothesis 1.
By calibrating the structural characteristics of historical load profiles with a scaling factor, it is possible to predict the required zonal powers with minimal error. This approach leverages persistent features observed in historical data to enable robust future forecasts.
2. Methodology for Determining the Necessary and Sufficient Volumes of Power in Integrated Power Systems for the Long Term
In our study, the generation of integrated power system is conceptually divided into three key zones: the base, half-peak and peak zones. The base zone is defined by a fixed number of hours corresponding to the steady load, while the half-peak and peak zones represent varying demand periods. The following mathematical model applies under the assumptions that the daily load profile can be segmented based on these zones and that the historical patterns are representative of the underlying operational conditions.
The task formulated in this study is the first stage of solving a major scientific problem of optimising the prospective power structure of the integrated power system. The purpose of this work is to determine the zonal power values that would be able to generate electricity in year x with an annual volume of electricity Wx. After determining these powers, it will be possible to start calculating the optimal sets of types and powers of generating sources based on a particular optimisation criterion.
When studying the problems of structural development of the IPS, one of the key ones is that the forecasted prospective volumes of electricity production are developed for the prospective year, while the reported retrospective information on its production is in the form of daily electrical load graphs (ELGs) for the past years. This circumstance radically complicates the problem of determining the necessary zonal power volumes of daily ELGs necessary and sufficient to meet the forecast annual demand for electricity.
2.1. Features of Daily ELGs
Daily ELGs have features that can be used to acceptably solve the above problem, both in terms of accuracy and labour intensity.
One of these features is that for each year x with annual electricity production Wx, there is only one daily ELGxmax with maximum daily production. Another feature of such ELGxmax is that its zonal powers, as well as their sum, are the largest compared to similar indicators of other daily ELGs of the same year. An important feature of the structure of each daily ELG is that its base zone is a clearly and unambiguously formed rectangle, with the width always being the number of hours in a day and the height being the power, which ensures the appropriate electricity generation in the base zone under such conditions. In the semi-peak and peak zones of daily ELGs, there is no such clarity; they have an openly irregular shape, but each of them, when solving the necessary tasks, is approximated by a rectangle whose height is the maximum power value of the corresponding ELG zone and whose width is the number of hours of the day during which the energy of this ELG zone is generated and the specified power is used (Figure 1).
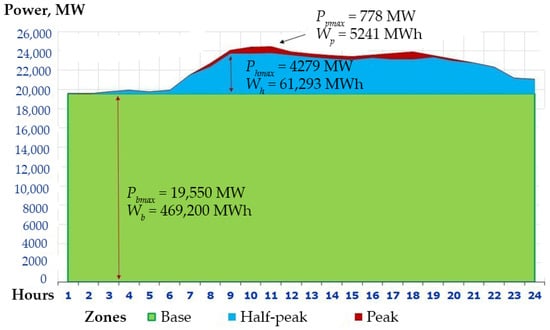
Figure 1.
Typical ELG in the IPS of Ukraine (data for 28 January 2019, day of the 2019 year with the maximum electricity production).
2.2. Methodology for Determining the Necessary and Sufficient Zonal Generation Based on the Forecasted Electricity Generation Volumes Wx in Year x
The analysis leads to the conclusion that the solution to the formulated problem will be ensured if, among all daily ELGx of year x, a daily ELGxmax is identified, with both zonal and total power volumes greater than the corresponding indicators of all other daily ELGs of this year. Indeed, the preceding analysis shows that this event occurs when the daily power generation on a certain (unknown) day is the highest in year x. This is true for both future and retrospective ELGs. As shown below, this is sufficient to develop both a methodology and a mathematical model for the task at hand.
The methodology for determining the necessary and sufficient volumes of zonal powers that are guaranteed to provide electricity generation in the amount of Wx in year x is as follows:
- On set N of retrospective data on all daily ELGi, where and i is the year index, one ELGimax with maximum electricity production is selected, which becomes the base by i year and ELGδi.
- On set of N retrospective ELGδi, , the indicators of the structure (weighting factors) of electricity production by zones l = b, h, p (designations for base, half-peak and peak zones, respectively) are determined.
- Using item 2 on the set of ELGδi, the indicators are averaged.
- On the set of N daily ELGδi, , the indicators of the daily duration of the maximum power for each of the zones l = b, h, p are determined.
- The daily load peak durations for all zones of daily base ELGδi are converted into annual ones with subsequent zonal averaging, resulting in three zonal averages of annual load peak durations Tbr0, Thr0, Tpr0.
- Using the volumes of electricity production and the indicators of items 3 and 5, the errors for all ELGδi of the set N are calculated.
- On the set of ELGδi, , one reference ELGδe with the best zonal error performance on the set of ELGδi is selected.
- Calibration of the forecasted production volumes Wx and annual reference production volumes Wδe is carried out with further determination of zonal powers, zonal volumes of electricity production forecast and relevant accuracy indicators.
3. Mathematical Model for Determining the Prospective Powers in the IPS Based on the Forecasted Generation Volumes
3.1. Determination of the Reference Daily ELGδi
The zonal coefficients are derived by first collecting historical daily load data and identifying the day with maximum production for each year. The daily load profile is then segmented into base, half-peak and peak zones. For each zone, the coefficient is calculated as the ratio of the zone’s load (conceptually the ‘area’ under the curve) to the total daily load. These coefficients are subsequently averaged over all historical years to minimise random fluctuations. The calibration factor (α) is later applied to these averaged coefficients to scale the historical data to the forecasted demand.
On the set of N daily ELGδi, three-dimensional vectors of the coefficients of the zonal structure of the required values are determined. In particular, the vector of electricity generation structure for ELGδi has the form
where the zonal coefficients Kwib, Kwih, Kwip are defined as follows:
On the set of N base of ELGsδi, the average indicators of the coefficients of the zonal structure of the annual electricity production of the base ELGsδi, are determined:
The average annual duration of maximum load usage in zones l = b, h, p of ELGδi is determined as follows:
Using the coefficients (5)–(7) and the actual annual electricity production Wi in year i, , zonal indicators are determined according to the following dependencies:
The availability of the calculated indicators (11)–(13) and (8)–(10) makes it possible to determine the zonal powers of the entire set of basic daily ELGδi, according to the following dependencies:
The basic ELGδi contains data on actual power indicators (14) and (15), which makes it possible to determine the methodological error of these dependencies in both absolute and relative terms:
where Δ is the absolute error, ψ is the relative error, l = b, h, p are notations for any zone of the ELG, and f is the designation for the actual value.
After determining the indicators (14)–(18) for all the ELGδi, the one with the smallest modules of indicators (18) is selected among them, and it is further used as a reference with the designation ELGδi.
3.2. Determination of the Necessary and Sufficient Zonal Power Volumes to Ensure the Forecast Electricity Production Wx in Year x
This task can be solved most effectively by calibrating the reference ELGie using the following algorithm. The calibration factor is determined by the formula
The calibration factor α is defined as the ratio of the forecasted annual demand to the historical annual production for the reference day. Its introduction is justified by the notion that historical load profiles, once adjusted for scale, maintain their inherent structure and relative distribution. This proportional scaling minimises error, as confirmed by our low error margins, and ensures the model’s predictive accuracy.
Since the maximum load lifetime for the base zone is a constant, the base zone power is automatically determined as
Because the dependence (19) can be used in the form , the powers Pxh and Pxp are defined as follows:
Using (20)–(22), we determine the zonal indicators of annual electricity production:
Thus, given the forecast value of annual electricity production Wx in year x, the zonal powers of the daily schedule with maximum electricity production ELGxmax are determined by multiplying the relevant zonal power indicators of the reference ELGie by the calibration factor according to (19)–(22). The zonal indicators of annual electricity production in the same year are determined similarly according to (23)–(25).
4. Modelling and Analysis
4.1. Modelling Results
To apply model (1)–(25), it is sufficient to have only one baseline retrospective ELGδi and one annual forward-looking electricity demand forecast Wx in year x.
This study used redundant arrays of initial retrospective information, namely, four basic ELGsδi and three forecasts Wx, to improve the accuracy of forecasting zonal power and generation indicators (Table 1 and Table 2).

Table 1.
Baseline information: annual zonal electricity production.

Table 2.
Baseline information: zonal structure of annual electricity production; actual zonal maximum power; annual zonal duration of maximum power use.
The use of the averaged indicators of the generation structure (5)–(7) and the averaged annual duration of the maximum zonal load (8)–(10) made it possible to simultaneously solve several important tasks: to prove that the sum of zonal generation indicators Ws for each of the ELGδi, with zero error coincides with the actual data of electricity production Wi in year i (Table 3) and to prove that the reference ELGδe (2019 year) has zonal generation and power errors that do not exceed 0.39% and 1.02% by modulo, respectively. This gives grounds for applying the specified dependencies to determine zonal generation and power indicators for the forecast annual generation volumes Wi in years i (Table 3 and Table 4).

Table 3.
Predictive annual zonal electricity generation volumes corresponding to base ELGδi of the given years.

Table 4.
Forecast of zonal powers of base ELGδi and determination of zonal errors of powers and electricity production.
However, the issue of errors in zonal indicators of annual electricity generation and zonal powers for future years remains unresolved. To solve it, the authors developed the calibration method (19)–(25), which generates forecasting errors of zonal generation and power at total future annual generation volumes Wx not worse than the errors of the reference ELGδe, namely, |Δ| ≤ 0.39% for generation and |Δ| ≤ 1.02% for power (Table 5 and Table 6).

Table 5.
Forecast of prospective annual zonal electricity production (×103 MWh) and zonal powers (MW) for the selected years by averaging the generation structure.

Table 6.
Estimation of relative errors in forecasting zonal electricity generation and zonal powers for selected years by the calibration method.
In assessing the level of error of the above indicators, we took into account a criterion that is widely used in feasibility studies. Competing long-term feasibility projects are considered equivalent if the errors in their key indicators do not exceed 5%.
Thus, the calibration method (19)–(25) developed and implemented in this study more than satisfies the above criterion of permissible error.
4.2. Scenario-Based Extensions
Although the presented approach relies on historical data which smooths out random variations, we recognise that renewable energy sources introduce inherent variability. While our method indirectly manages such fluctuations through averaging, future research should consider integrating stochastic models to account explicitly for renewable generation variability.
In order to account for unforeseen external factors that might affect future electricity consumption—such as a post-war drop in demand or a surge in electric vehicle adoption—we introduce an adjustment factor (δ). By redefining the forecasted annual production as Wₓn = δ × Wₓ, different scenarios can be simulated. For example, a δ less than 1 may simulate reduced demand after economic shocks, whereas a δ greater than 1 can represent increased demand due to additional loads.
5. Conclusions
Electricity is an essential, technologically advanced commodity. Activities in the electricity sector provide high added value. Power generation equipment is high-tech and expensive. The residual life of the equipment of the power system, which is comparable to the Ukrainian one, is estimated to be around USD 80–100 billion. In the context of the post-war restoration of the power system of Ukraine, the required investment will increase at least threefold. Under such conditions, the requirements for the accuracy of the models used to forecast the future structure of the power system’s generating powers will be significantly increased. While in peacetime the permissible error in determining zonal powers could be up to 5%, in the context of the power system restoration, such an error could result in USD 12–15 billion of additional investments. This would be extremely undesirable in the post-war period.
Therefore, over the course of this study, a methodology and a mathematical model were developed and synthesised to determine the necessary and sufficient zonal powers that ensure predetermined volumes of electricity production with an accuracy limited only by the accuracy of the initial information.
Two methods were used to achieve these results within the same model. In the first stage, the least squares method (averaging) was used to identify the reference ELG from the set of base ELGδi, . The detected ELGie has the lowest errors in power and generation modules compared to other base ELGδi. In this way, the errors of the initial information are filtered (minimised).
In the second stage of calculations using this model, the calibration method was used. This new method virtually identically transfers the indicators from the accuracy of the reference ELGie to the ELGxmax of the daily maximum electricity generation at its annual production Wx in year x. It is the organic combination of these methods within one model that ensures the obtaining of zonal power indicators and, as a result, the generation of the daily ELGxmax with an accuracy limited only by the errors of the initial information of the retrospective daily base ELGδi, . The application of the developed model to the real data of the Ukrainian power system (Table 1 and Table 2) showed that it forms decisions on zonal power Pxl and generation Wxl with high accuracy, namely, the error of zonal power by module does not exceed 1.02% and generation −0.39% (Table 5 and Table 6).
In the future, to solve the problem of optimising the structure of power system generating powers for a given period with a given electricity production, it is necessary to use this model to determine the necessary and sufficient zonal powers and then to optimise the structure of its generation for each zone using universal software systems.
While our model demonstrates very low forecasting errors, it relies on the assumption that historical load patterns will persist into the future. Changes due to increased renewable penetration, evolving economic conditions or other unforeseen factors may affect its accuracy. Future work should explore integrating external variables such as meteorological or policy factors and incorporate more dynamic, stochastic models to further enhance forecast robustness and scalability across different integrated power systems.
Author Contributions
Conceptualisation, A.Z., M.K. and V.D.; methodology, A.Z. and V.D.; software, V.D.; validation, A.Z., V.B. and V.D.; formal analysis, M.K. and V.B.; investigation, A.Z., M.K., V.B. and V.D.; resources, V.D.; data curation, M.K. and V.D.; writing—original draft preparation, A.Z. and V.D.; writing—review and editing, A.Z. and V.B.; visualisation, A.Z. and M.K.; supervision, M.K.; project administration, A.Z.; funding acquisition, A.Z. and V.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to special restrictions on access to data regarding the functioning of critical infrastructure.
Acknowledgments
This work was supported by projects “Integrated modeling for robust management of food-energy-water-social-environmental (FEWSE) nexus security and sustainable development” (IIASA-NASU, 22-501 (R-45-T)), “Comprehensive analysis of robust preventive and adaptive measures of food, energy, water and social management in the context of systemic risks and consequences of COVID-19” (0122U000552, 2022–2026), and “Development of the structure and ensuring the functioning of self-sufficient distributed generation” (0125U001572, 2025–2026), which are financed by National Academy of Science of Ukraine.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ELG | electrical load graph |
| GDP | gross domestic product |
| IPS | integrated power systems |
References
- Hotra, O.; Kulyk, M.; Babak, V.; Kovtun, S.; Zgurovets, O.; Mroczka, J.; Kisala, P. Organisation of the Structure and Functioning of Self-Sufficient Distributed Power Generation. Energies 2024, 17, 27. [Google Scholar] [CrossRef]
- Denysov, V.; Kulyk, M.; Babak, V.; Zaporozhets, A.; Kostenko, G. Modeling Nuclear-Centric Scenarios for Ukraine’s Low-Carbon Energy Transition Using Diffusion and Regression Techniques. Energies 2024, 17, 5229. [Google Scholar] [CrossRef]
- Babak, V.P.; Babak, S.V.; Eremenko, V.S.; Kuts, Y.V.; Myslovych, M.V.; Scherbak, L.M.; Zaporozhets, A.O. Models of Measuring Signals and Fields. In Models and Measures in Measurements and Monitoring; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2021; Volume 360. [Google Scholar] [CrossRef]
- Babak, V.P.; Kulyk, M.M. Possibilities and Perspectives of the Consumers-Regulators Application in Systems of Frequency and Power Automatic Regulation. Tekhnichna Elektrodynamika 2023, 2023, 72–80. [Google Scholar] [CrossRef]
- Nikitin, Y.; Yevtukhova, T.; Novoseltsev, O.; Komkov, I. Regional Energy Efficiency Programs. Current Status and Development Prospects. Energy Technol. Resour. Sav. 2024, 78, 34–47. [Google Scholar] [CrossRef]
- Bielokha, H.; Chupryna, L.; Denisyuk, S.; Eutukhova, T.; Novoseltsev, O. Hybrid energy systems and the logic of their service-dominant implementation: Screening the pathway to improve results. Energy Eng. 2023, 120, 1307–1323. [Google Scholar] [CrossRef]
- Denysov, V.; Babak, V.; Zaporozhets, A.; Nechaieva, T. Quasi-dynamic Energy Complexes Optimal Use on the Forecasting. In Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; pp. 81–107. [Google Scholar] [CrossRef]
- Denysov, V.; Babak, V.; Zaporozhets, A.; Nechaieva, T. Energy System Optimization Potential with Consideration of Technological Limitations. In Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; pp. 113–126. [Google Scholar] [CrossRef]
- Zaporozhets, A.; Babak, V.; Kostenko, G.; Zgurovets, O.; Denisov, V.; Nechaieva, T. Power System Resilience: An Overview of Current Metrics and Assessment Criteria. In Systems, Decision and Control in Energy VI. Studies in Systems, Decision and Control; Babak, V., Zaporozhets, A., Eds.; Springer: Cham, Switzerland, 2024; Volume 561. [Google Scholar] [CrossRef]
- Zaporozhets, A.; Kostenko, G.; Zgurovets, O.; Deriy, V. Analysis of Global Trends in the Development of Energy Storage Systems and Prospects for Their Implementation in Ukraine. In Power Systems Research and Operation. Studies in Systems, Decision and Control; Kyrylenko, O., Denysiuk, S., Strzelecki, R., Blinov, I., Zaitsev, I., Zaporozhets, A., Eds.; Springer: Cham, Switzerland, 2024; Volume 512. [Google Scholar] [CrossRef]
- Kumar, J.K.; Ravi, G. A Simple Regression Model for Electrical Energy Forecasting. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2014, 3, 11331–11335. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.; Song, K.; Guan, D.; Zhang, N.; Ye, P.; Li, D.; Man, L.; Xu, X. Forecast Analysis of Regional Energy Demand Based on Grey Linear Regression Forecast Model. IOP Conf. Ser. Earth Environ. Sci. 2021, 645, 012047. [Google Scholar] [CrossRef]
- Sahraei, M.A.; Duman, H.; Çodur, M.Y.; Eyduran, E. Prediction of transportation energy demand: Multivariate Adaptive Regression Splines. Energy 2021, 224, 120090. [Google Scholar] [CrossRef]
- Panigrahi, R.; Patne, N.R.; Pemmada, S.; Manchalwar, A.D. Regression model-based hourly aggregated electricity demand prediction. Energy Rep. 2022, 8, 16–24. [Google Scholar] [CrossRef]
- Fan, W.; Wu, X.; Shi, X.Y.; Zhang, C.; Hung, I.W.; Leung, Y.K.; Zeng, L.S. Support vector regression model for flight demand forecasting. Int. J. Eng. Bus. Manag. 2023, 15, 84797902311743. [Google Scholar] [CrossRef]
- Hu, Y.-C.; Chiu, Y.-J.; Yu, C.-Y.; Tsai, J.-F. Integrating Nonlinear Interval Regression Analysis with a Remnant Grey Prediction Model for Energy Demand Forecasting. Appl. Artif. Intell. 2021, 35, 1490–1507. [Google Scholar] [CrossRef]
- Rao, C.; Zhang, Y.; Wen, J.; Xiao, X.; Goh, M. Energy demand forecasting in China: Asupport vector regression-compositional data second exponential smoothing model. Energy 2023, 263, 125955. [Google Scholar] [CrossRef]
- Storcz, T.; Kistelegdi, I.; Horváth, K.R.; Ercsey, Z. Applicability of Multivariate Linear Regression in Building Energy Demand Estimation. Math. Model. Eng. Probl. 2022, 9, 1451–1458. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karamousantas, D.C.; Chatzarakis, G.E.; Katsikas, S.K.; Liatsis, P. Electricity demand loads modeling using AutoRegressive Moving Average (ARMA) models. Energy 2008, 33, 1353–1360. [Google Scholar] [CrossRef]
- Seong, B. Smoothing and forecasting mixed-frequency time series with vector exponential smoothing models. Econ. Model. 2020, 91, 463–468. [Google Scholar] [CrossRef]
- Mi, J.; Fan, L.; Duan, X.; Qiu, Y. Short-Term Power Load Forecasting Method Based on Improved Exponential Smoothing Grey Model. Math. Probl. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Zheng, X.; Jin, T. A reliable method of wind power fluctuation smoothing strategy based on multidimensional non-linear exponential smoothing short-term forecasting. IET Renew. Power Gener. 2022, 16, 3573–3586. [Google Scholar] [CrossRef]
- Saglam, M.; Lv, X.; Spataru, C.; Karaman, O.A. Instantaneous Electricity Peak Load Forecasting Using Optimization Machine Learning. Energies 2024, 17, 777. [Google Scholar] [CrossRef]
- Kyi, S.; Taparugssanagorn, A. IoT and machine learning models for multivariate very short-term time series solar power forecasting. IET Wirel. Sens. Syst. 2024, 14, 381–395. [Google Scholar] [CrossRef]
- Benti, N.E.; Chaka, M.D.; Semie, A.G. Forecasting Renewable Energy Generation with Machine Learning and Deep Learning: Current Advances and Future Prospects. Sustainability 2023, 15, 7087. [Google Scholar] [CrossRef]
- Mostafavi, E.S.; Mostafavi, S.I.; Jaafari, A.; Hosseinpour, F. Anovel machine learning approach for estimation of electricity demand: An empirical evidence from Thailand. Energy Convers. Manag. 2013, 74, 548–555. [Google Scholar] [CrossRef]
- Kheirkhah, A.; Azadeh, A.; Saberi, M.; Azaron, A.; Shakouri, H. Improved estimation of electricity demand function by using of artificial neural network principal component analysis data envelopment analysis. Comput. Ind. Eng. 2013, 64, 425–441. [Google Scholar] [CrossRef]
- Solyali, D. A Comparative Analysis of Machine Learning Approaches for Short-/Long-Term Electricity Load Forecasting in Cyprus. Sustainability 2020, 12, 3612. [Google Scholar] [CrossRef]
- El-Azab, H.-A.I.; Swief, R.; El-Amary, N.H.; Temraz, H. Machine deep learning approaches for forecasting electricity price energy load assessment on real datasets. Ain Shams Eng. J. 2024, 15, 102613. [Google Scholar] [CrossRef]
- Ortiz-Arroyo, D.; Skov, M.; Huynh, Q. Accurate Electricity Load Forecasting with Artificial Neural Networks. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 94–99. [Google Scholar] [CrossRef]
- Hu, H.; Gong, S.; Taheri, B. Energy demand forecasting using convolutional neural network and modified war strategy optimization algorithm. Heliyon 2024, 10, e27353. [Google Scholar] [CrossRef]
- Jain, A.; Gupta, S.C. Evaluation of electrical load demand forecasting using various machine learning algorithms. Front. Energy Res. 2024, 12, 1408119. [Google Scholar] [CrossRef]
- Mohammed, N.A.; Al-Bazi, A. An adaptive backpropagation algorithm for long-term electricity load forecasting. Neural Comput. Appl. 2022, 34, 477–491. [Google Scholar] [CrossRef]
- Plaga, L.S.; Bertsch, V. Methods for assessing climate uncertainty in energy system models—A systematic literature review. Appl. Energy 2023, 331, 120384. [Google Scholar] [CrossRef]
- Pilpola, S.; Lund, P.D. Analyzing the effects of uncertainties on the modelling of low-carbon energy system pathways. Energy 2020, 201, 117652. [Google Scholar] [CrossRef]
- Zapata, V.; Gernaat, D.E.H.J.; Yalew, S.G.; da Silva, S.R.S.; Iyer, G.; Hejazi, M.; van Vuuren, D.P. Climate change impacts on the energy system: A model comparison. Environ. Res. Lett. 2022, 17, 034036. [Google Scholar] [CrossRef]
- Senatla, M.; Bansal, R.C. Review of planning methodologies used for determination of optimal generation capacity mix: The cases of high shares of PV and wind. IET Renew. Power Gener. 2018, 12, 1222–1233. [Google Scholar] [CrossRef]
- Nema, P.; Nema, R.K.; Rangnekar, S. A current and future state of art development of hybrid energy system using wind and PV-solar: A review. Renew. Sustain. Energy Rev. 2009, 13, 2096–2103. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Rubasinghe, O.; Liu, Y.; Chow, Y.H.; Iu, H.H.C.; Fernando, T. Long-Term Energy and Peak Power Demand Forecasting Based on Sequential-XGBoost. IEEE Trans. Power Syst. 2024, 39, 3088–3104. [Google Scholar] [CrossRef]
- Sánchez-Durán, R.; Luque, J.; Barbancho, J. Long-Term Demand Forecasting in a Scenario of Energy Transition. Energies 2019, 12, 3095. [Google Scholar] [CrossRef]
- Ramos, H.M.; Pina, J.; Coronado-Hernández, O.E.; Pérez-Sánchez, M.; McNabola, A. Conceptual Hybrid Energy Model for Different Power Potential Scales: Technical Economic Approaches. Renew. Energy 2024, 237, 121486. [Google Scholar] [CrossRef]
- Advanced and Comprehensive World-Class Simulation Package CYME 9.0 Rev.4-Damas Wiki. Available online: https://www.damaswiki.net/node/282031 (accessed on 26 June 2025).
- DIgSILENT Power Generation. Power System Solutions DIgSILENT. Available online: https://www.digsilent.de/en/power-generation.html (accessed on 26 June 2025).
- The Electricity Market Model EMMA. The European Electricity Market Model. Available online: https://emma-model.com/explained/ (accessed on 26 June 2025).
- Denysov, V.; Babak, V. Software and information simulation complex GEINASU SIC of multi-node integrated and autonomous power and heat supply systems. Syst. Res. Energy 2023, 2023, 50–63. [Google Scholar] [CrossRef]
- The Enertile Optimisation Model. Enertile® Website. Available online: https://enertile.eu/enertile-en/methodology/optimisation.php (accessed on 26 June 2025).
- ENTIGRIS an Electricity Market Model for Analyzing Energy Systems from an Economic Perspective. Wissensplattform-Digitalisierung Energiewendebauen. Available online: https://wissen-digital-ewb.de/en/tool_list/businessApps/793 (accessed on 26 June 2025).
- Loulou, R.; Labriet, M. ETSAP-TIAM: The TIMES integrated assessment model Part I: Model structure. Comput. Manag. Sci. 2007, 5, 7–40. [Google Scholar] [CrossRef]
- Loulou, R. ETSAP-TIAM: The TIMES integrated assessment model. part II: Mathematical formulation. Comput. Manag. Sci. 2007, 5, 41–66. [Google Scholar] [CrossRef]
- TIMES Ukraine. Available online: https://www.timesukraine.tokni.com/about (accessed on 26 June 2025).
- GENESYS Model. Northwest Power and Conservation Council. Available online: https://www.nwcouncil.org/2021powerplan_genesys-model/ (accessed on 26 June 2025).
- ARTEMIS|CPU-BASED ELECTRICAL TOOLBOX. OPAL-RT. Available online: https://www.opal-rt.com/solver/ (accessed on 26 June 2025).
- LIBEMOD-Frischsenteret. Forside-Frischsenteret. Available online: https://www.frisch.uio.no/ressurser/LIBEMOD/About%20the%20model/ (accessed on 26 June 2025).
- Svendsen, H.; Power Grid and Market Analysis (PowerGAMA). SINTEF. Available online: https://www.sintef.no/en/software/power-grid-and-market-analysis-powergama/ (accessed on 26 June 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).