Secure Optimization Dispatch Framework with False Data Injection Attack in Hybrid-Energy Ship Power System Under the Constraints of Safety and Economic Efficiency
Abstract
1. Introduction
1.1. Related Work on Abnormal Data Detection and Recovery
1.2. Related Work on Hybrid-Energy Ship System Optimization
1.3. Limitations of the Current Work
1.4. Motivation and Contribution
- A novel secure two-stage optimization dispatch model for HESPS is constructed. In contrast to existing work, this paper represents a pioneering effort in considering the safe and optimized scheduling of hybrid-energy ship power systems amidst cyber-physical risks.
- A spatial-temporal deep learning model using the WOA-CNN-LSTM is developed for identifying the false data under FDIAs. Compared with the existing methods, this method combines the advantages of CNN and LSTM to improve the data processing power, while avoiding the difficulty of hyperparameter selection.
- An IMOWOA-based optimization dispatch model is developed to achieve the joint optimization of optimal power flow and voyage for HESPS. Compared with the existing methods, the proposed method can effectively avoid falling into the local optima in the optimization process.
- Simulation tests demonstrate that the proposed secure two-stage optimization dispatch framework can not only accurately correct tampered data under FDIAs, but also can reduce the GHG emissions, costs, and power loss for HESPS at least by 1.96%, 5.67%, and 1.65%, respectively.
2. Problem Statement
2.1. Covert Characteristics of FDIAs
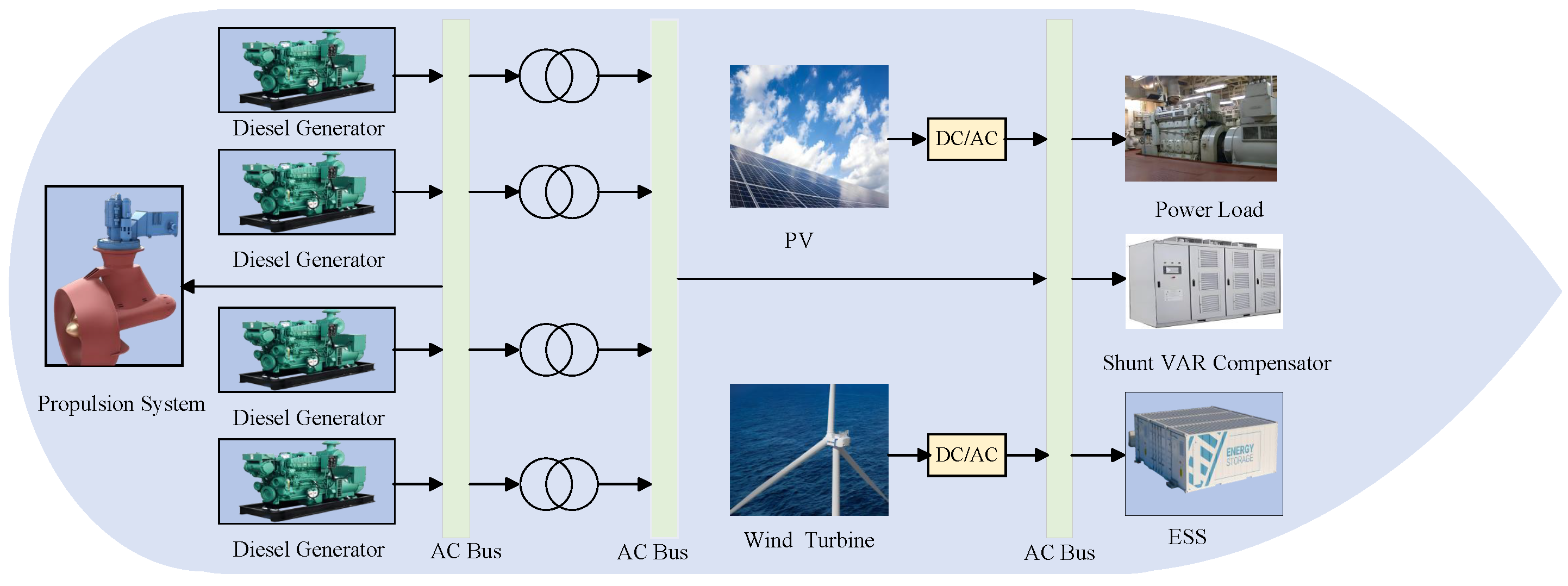
2.2. Hybrid-Energy Ship System Model
2.2.1. Diesel Generator System
2.2.2. Energy Storage System
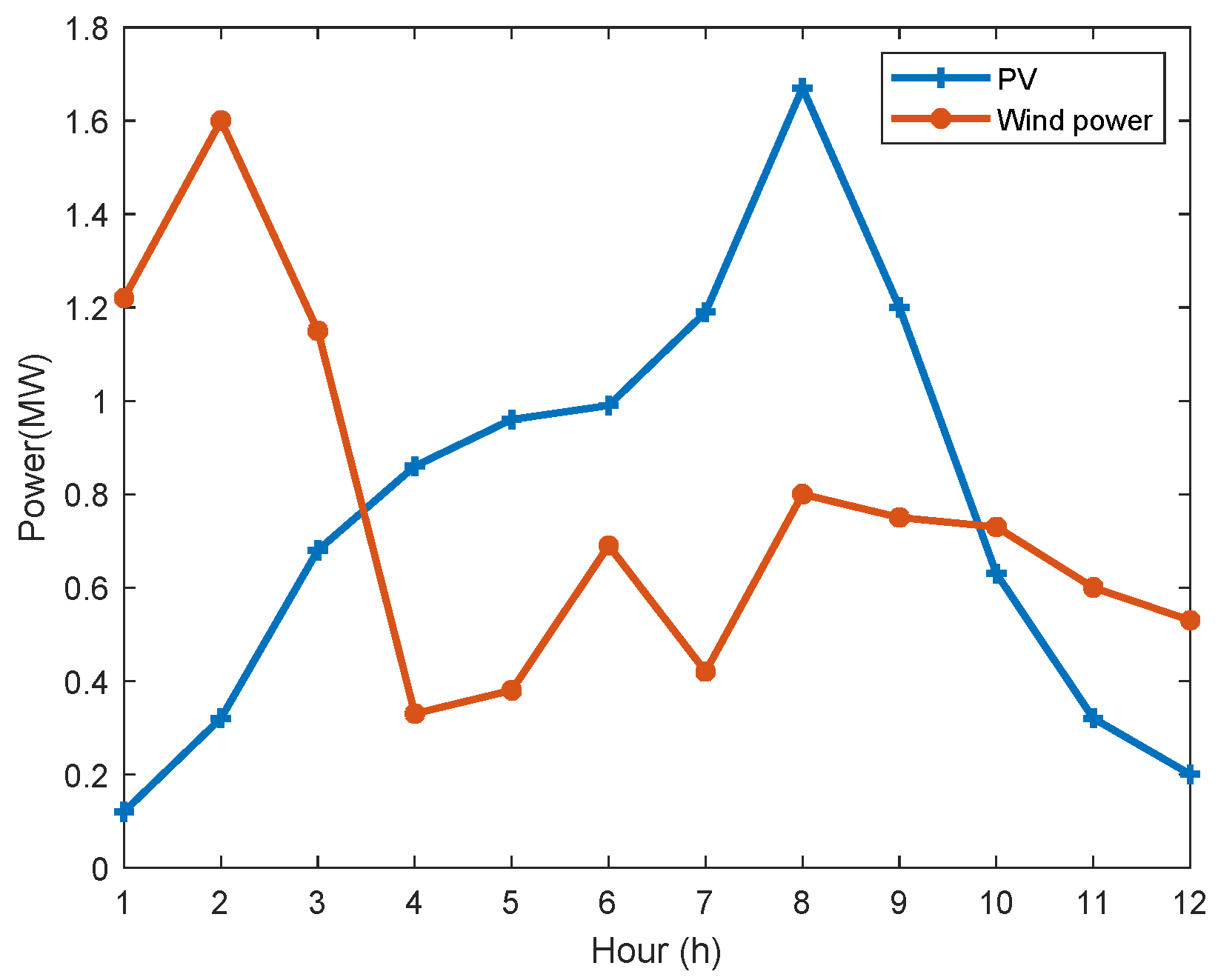
2.2.3. Wind Power System
2.2.4. Photovoltaic System
2.2.5. Propulsion System
2.3. The Problem of Joint Secure Optimization of Optimal Power Flow and Voyage for HESPS
2.3.1. Generator Constraints
2.3.2. Energy Storage System Constraints
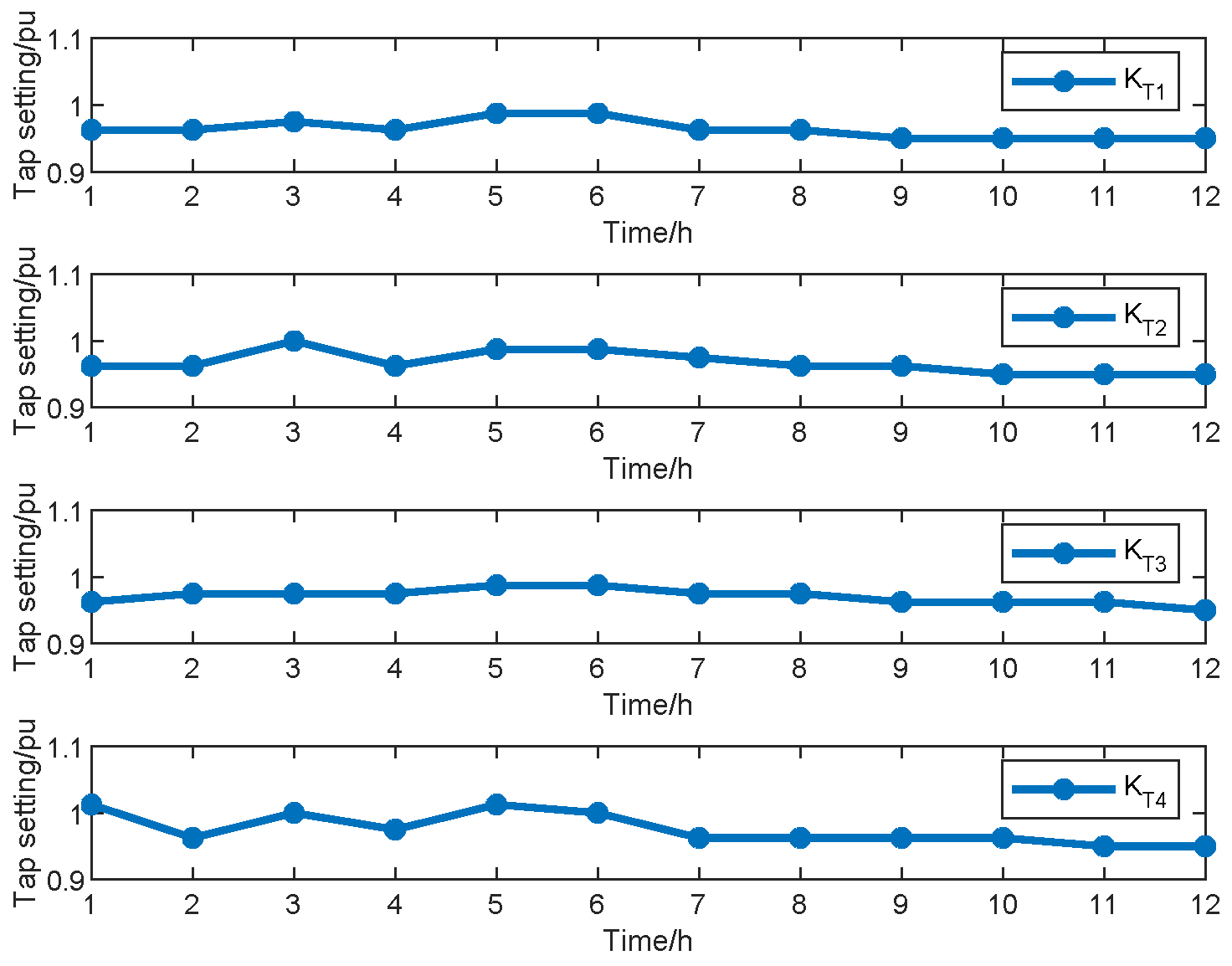
2.3.3. Transformer Constraint
2.3.4. Shunt VAR Compensator Constraint
2.3.5. Ship Velocity Constraint
2.3.6. Voyage Distance Constraint
2.3.7. Power Balance Constraints
2.3.8. Greenhouse Gas Emission Constrains
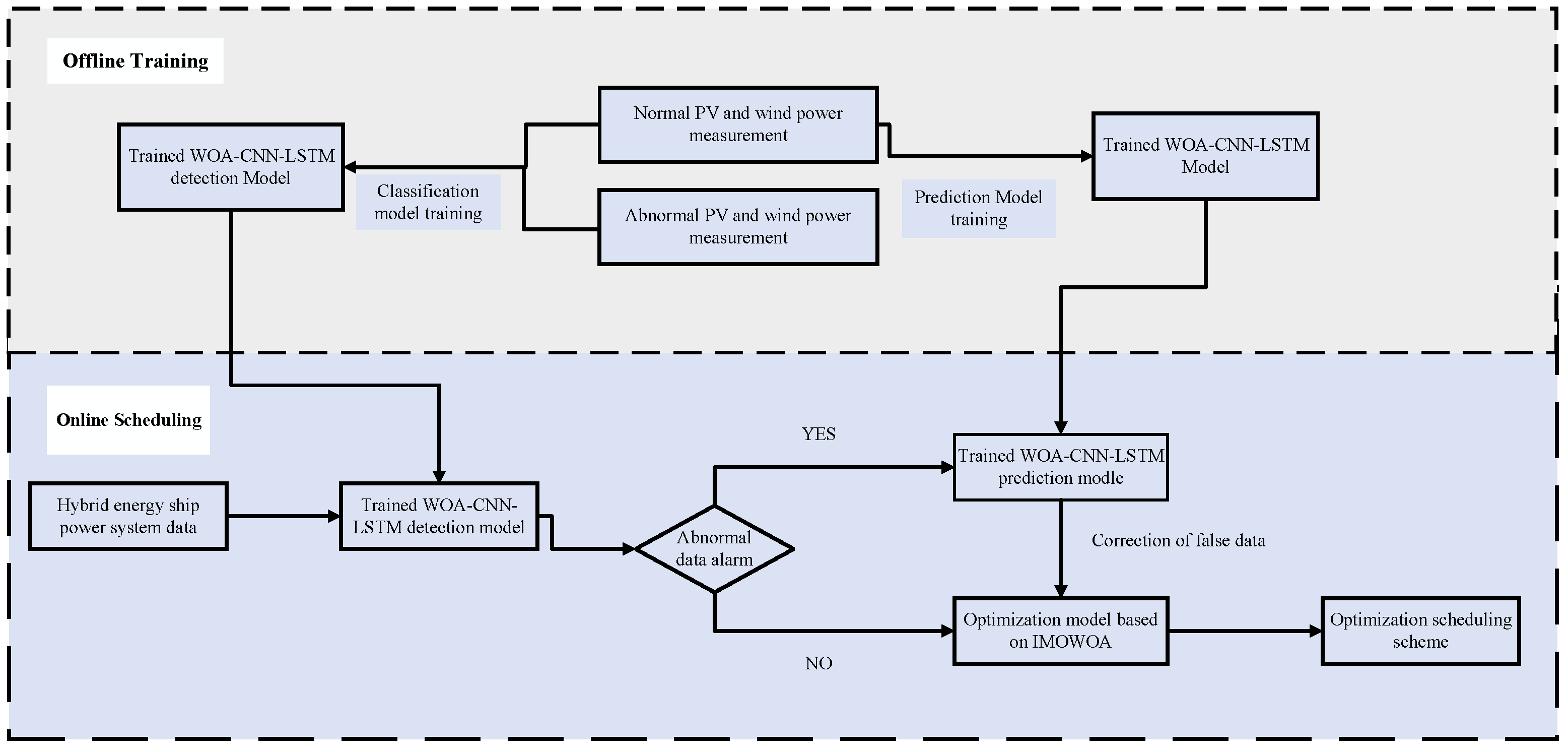
3. A Two-Stage Secure Optimization Dispatch Framework for HESPS Under FDIAs
3.1. WOA-CNN-LSTM Detection and Recovery Model
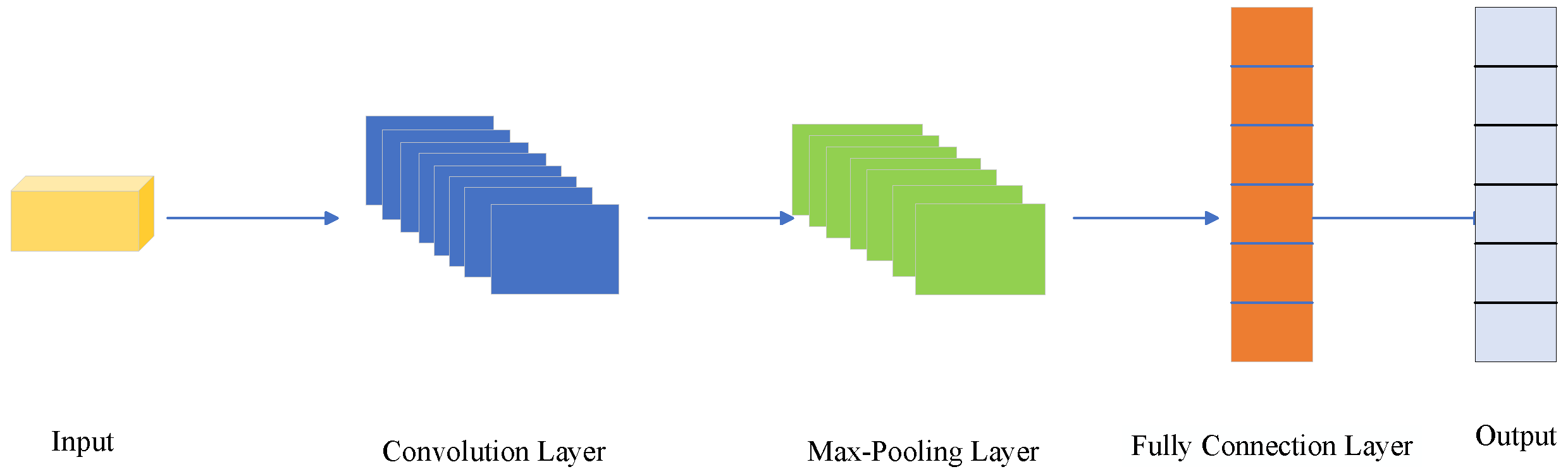
3.1.1. Convolutional Neural Network (CNN)
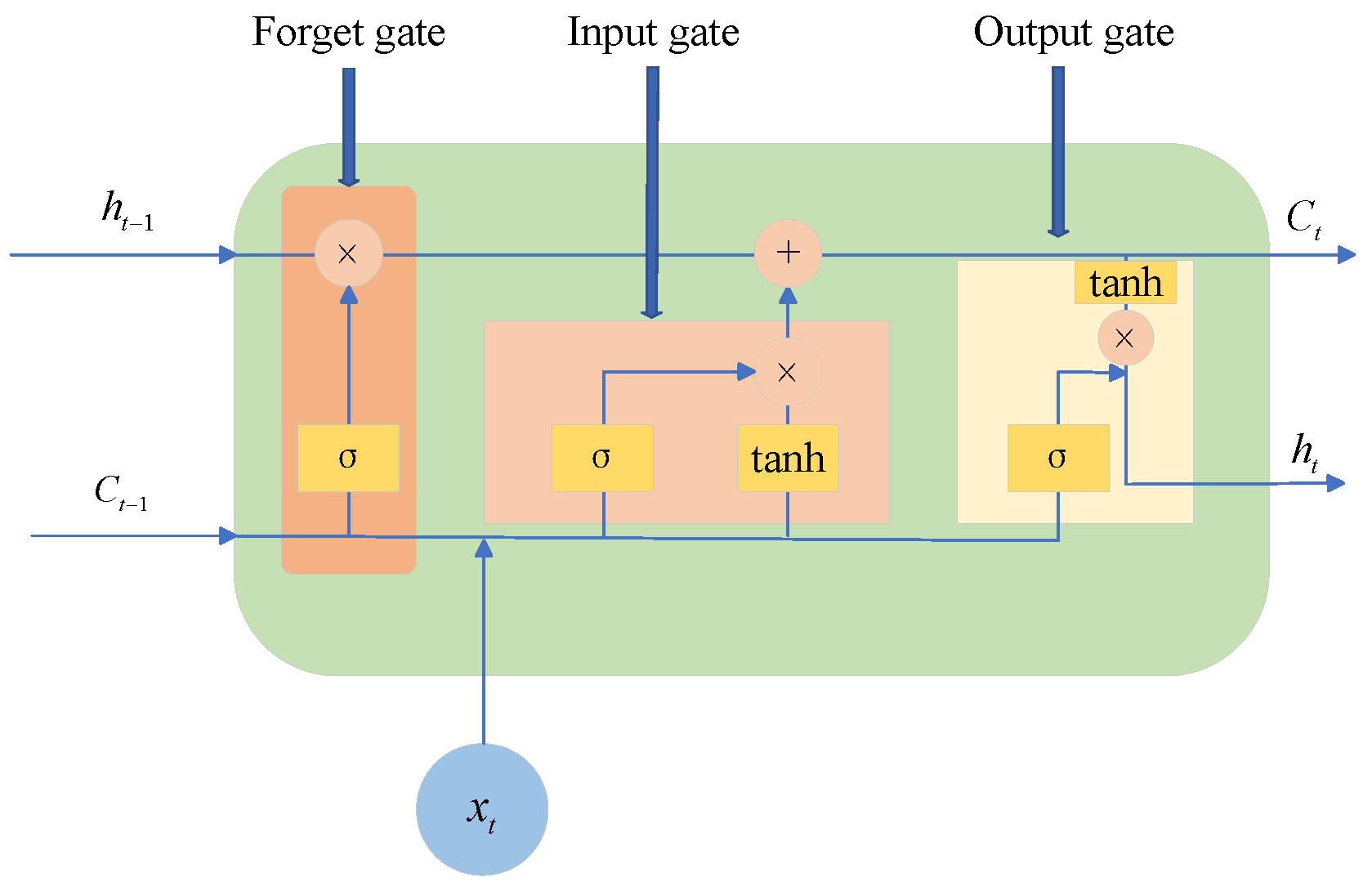
3.1.2. Long Short-Term Memory Neural Network Model
3.1.3. Whale Optimization Algorithm
3.2. False Data Identification Based on WOA-CNN-LSTM Detection Model
3.3. False Data Recovery Based on WOA-CNN-LSTM Prediction Model
3.4. Optimization Scheduling Model Based on Improved Multi-Objective Whale Optimization Algorithm
Improved Multi-Objective Whale Optimization Algorithm
3.5. The Proposed Secure Two-Stage Optimization Dispatch Algorithm for HESPS
| Algorithm 1 The secure two-stage optimization scheduling algorithm for HESPS |
|
- Step 1: Train the offline WOA-CNN-LSTM detection and recovery model;
- Step 2: WOA-CNN-LSTM-based data detection and recovery;
- Step 4: Initialize the related parameters, such as ESS, PV, etc.;
- Step 6: Search for the Pareto front by using the IMOWOA;
- Step 7: Output the optimal optimization solution for cost, power loss, etc.
3.6. Discussion of the Application of the Proposed Method to a Real System
4. Case Analysis
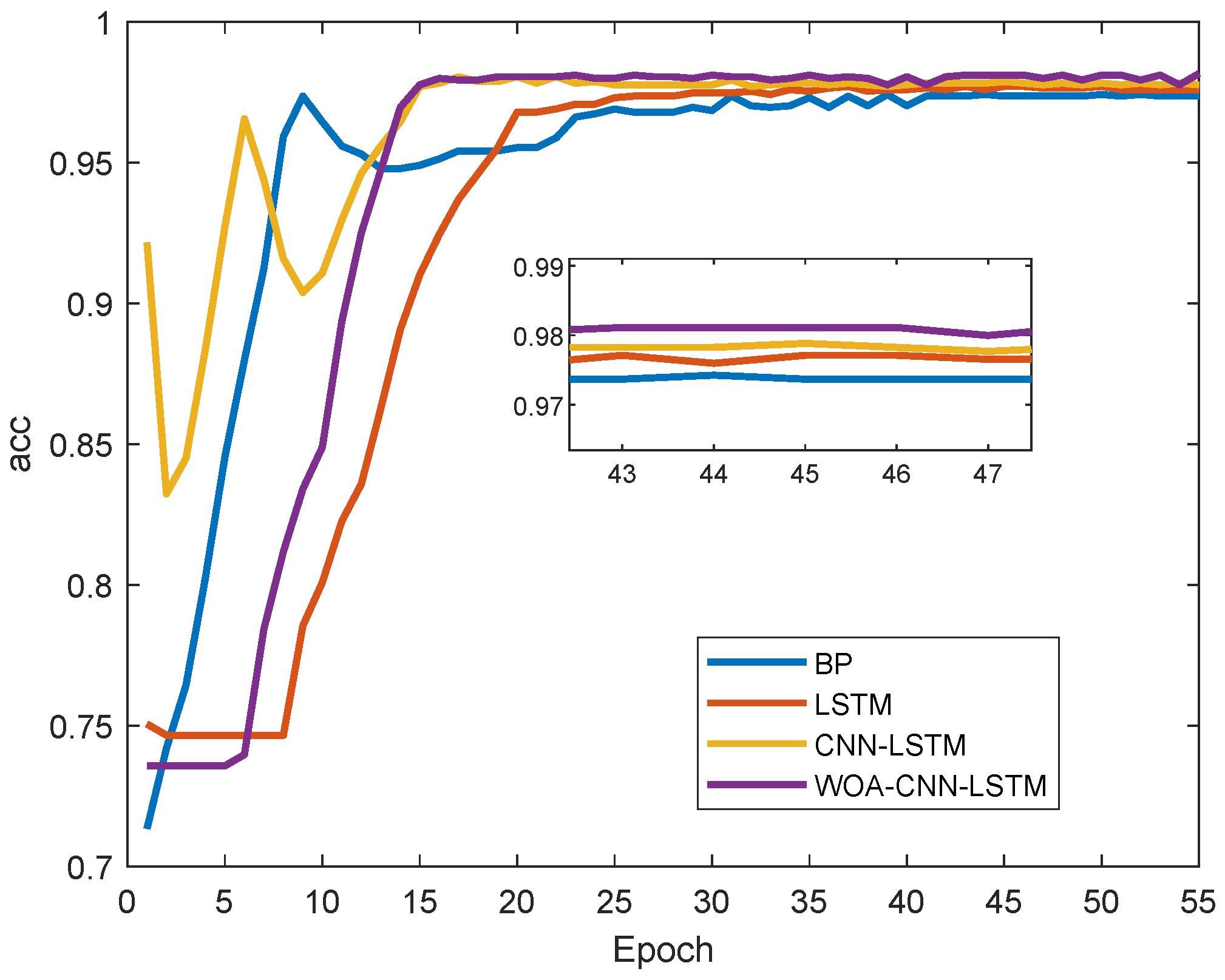
4.1. Performance Test for Identification of False Data Under FDIAs
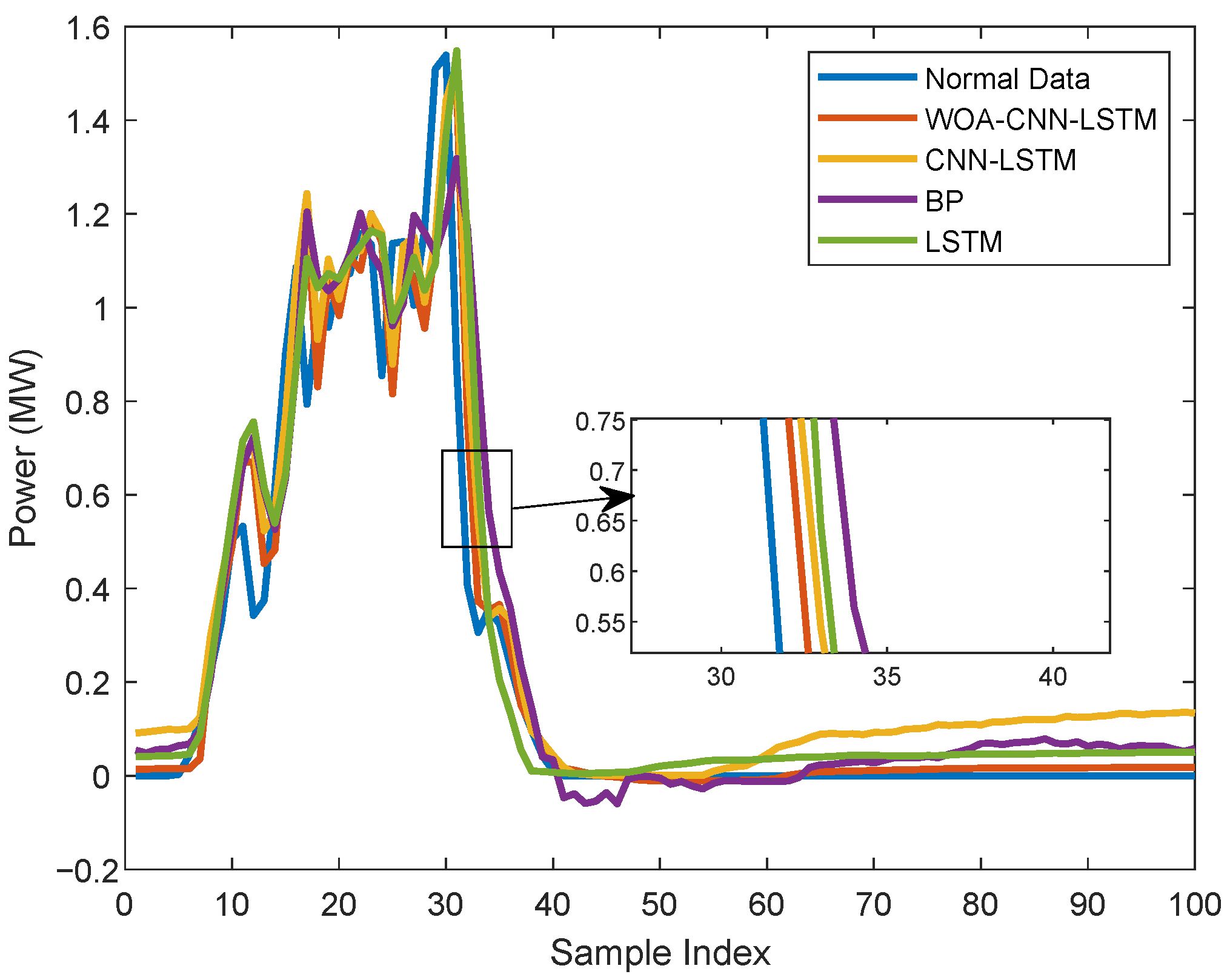
4.2. Performance Test for Data Recovery Based on WOA-CNN-LSTM Prediction Model
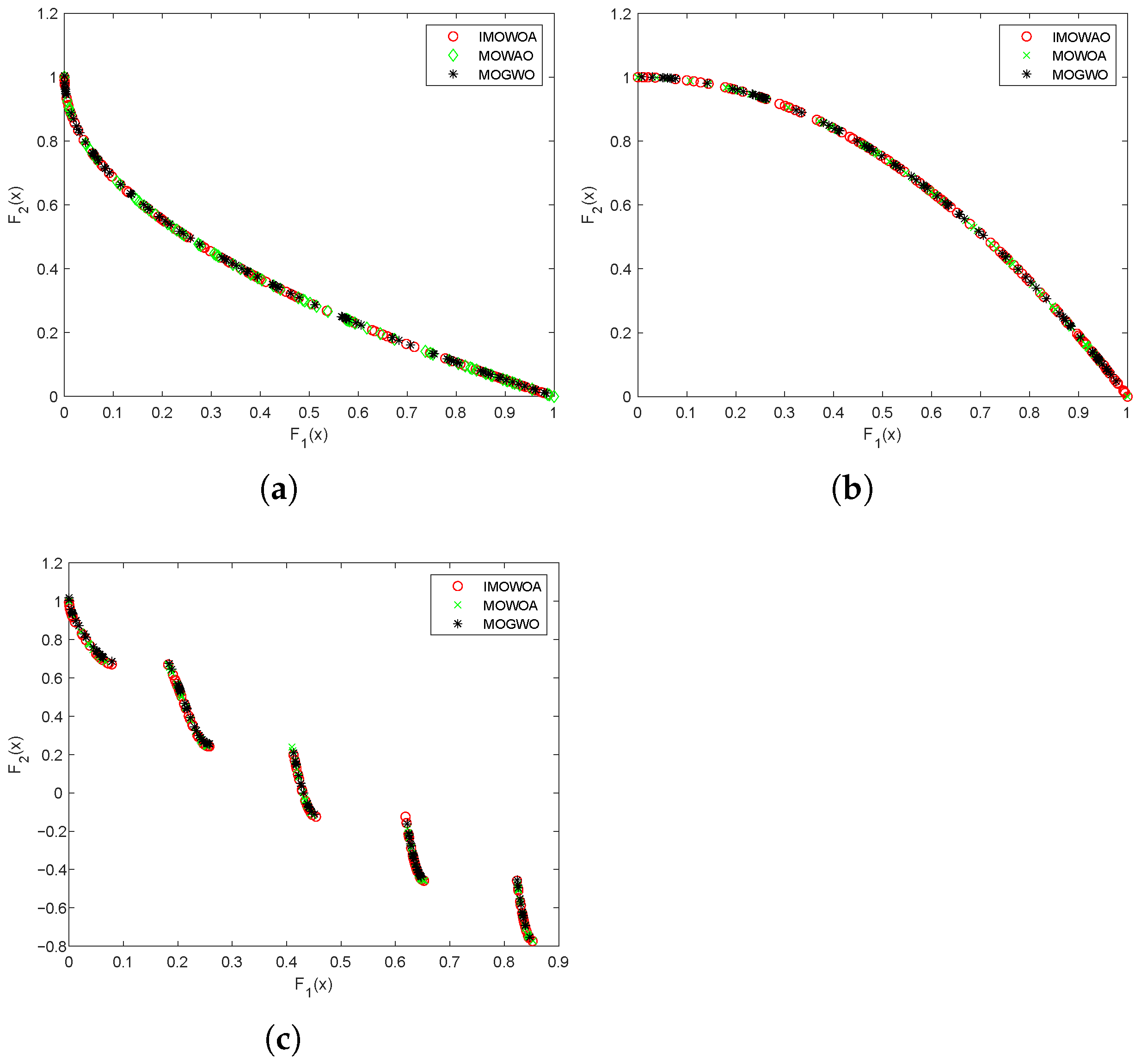
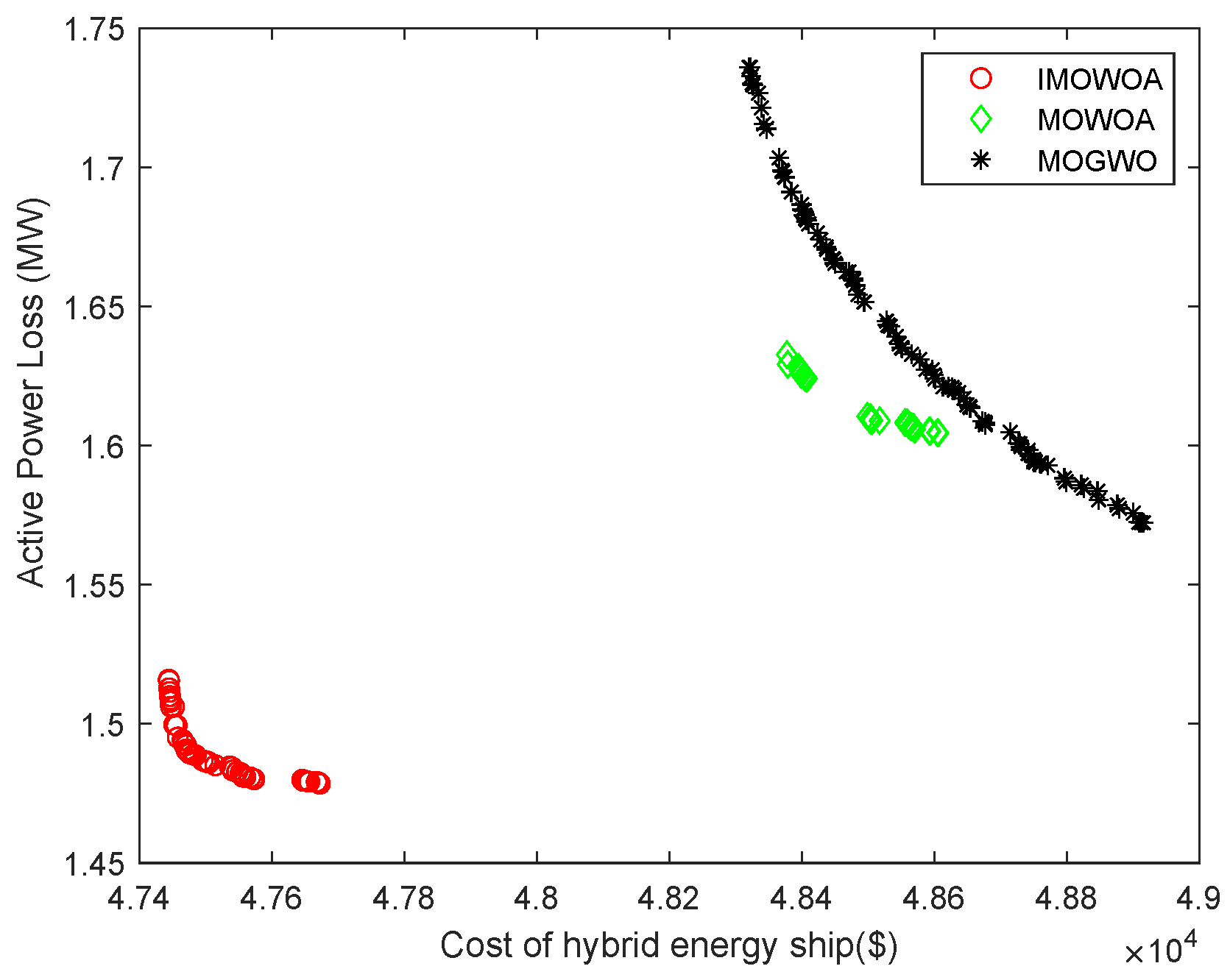
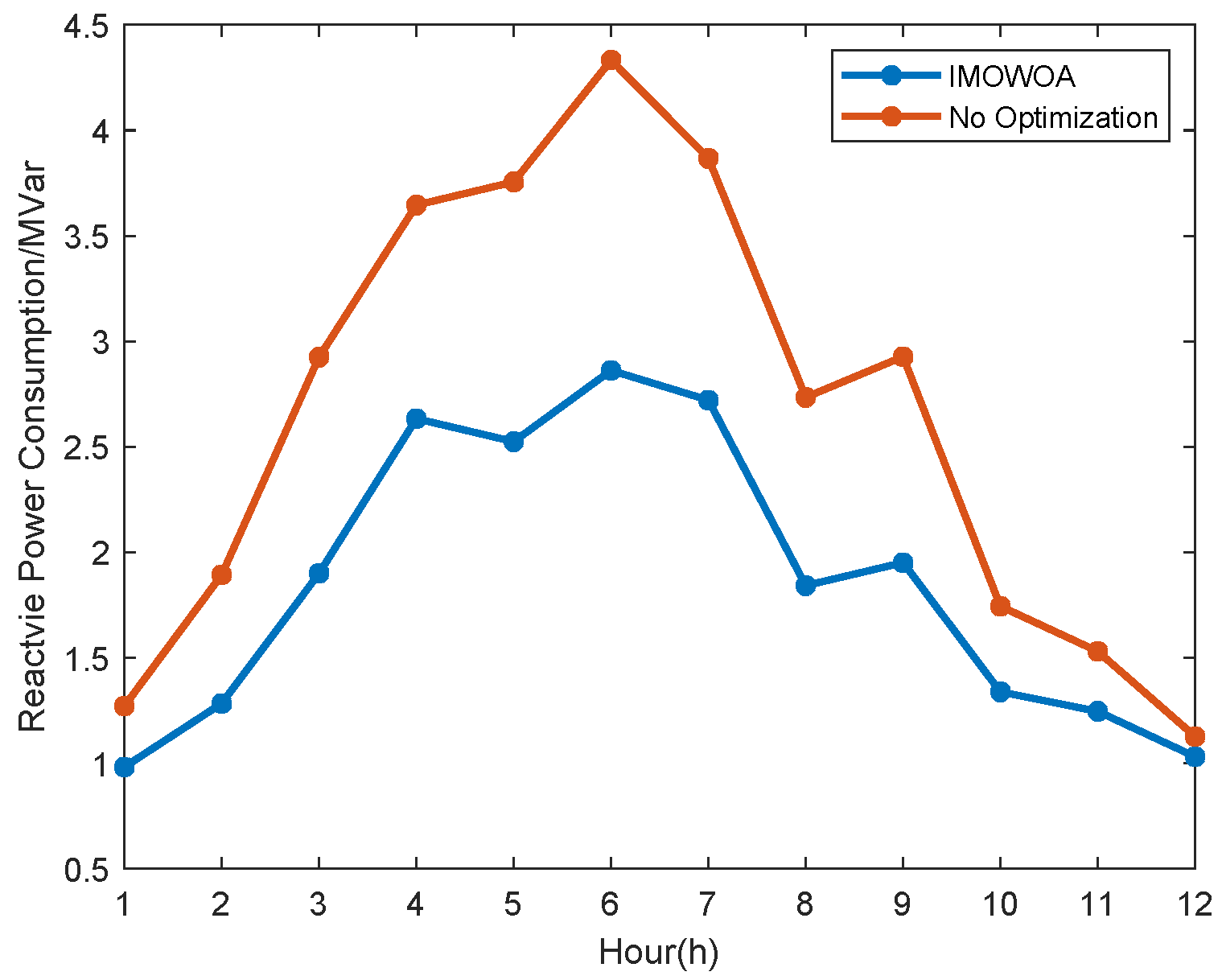
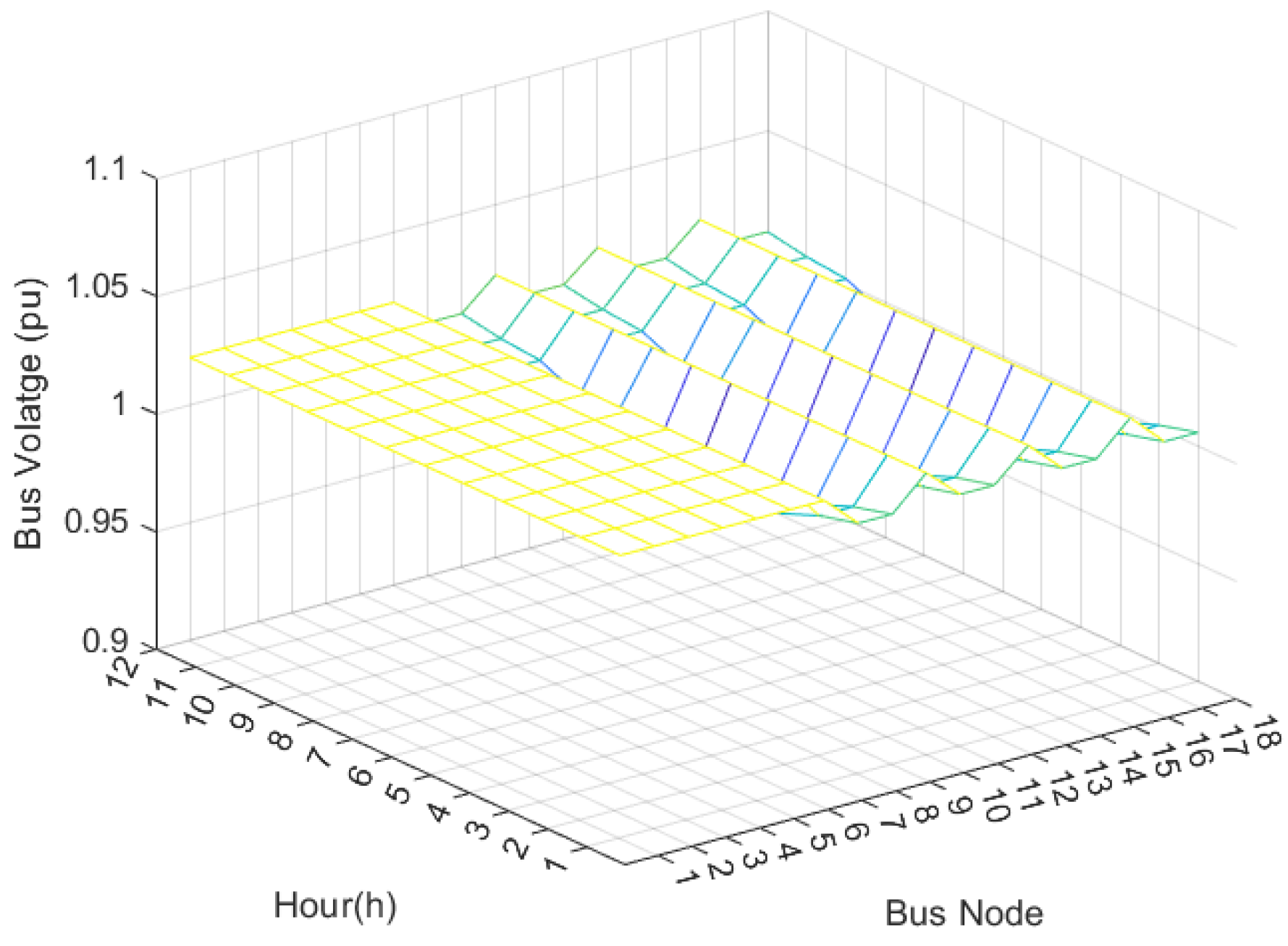
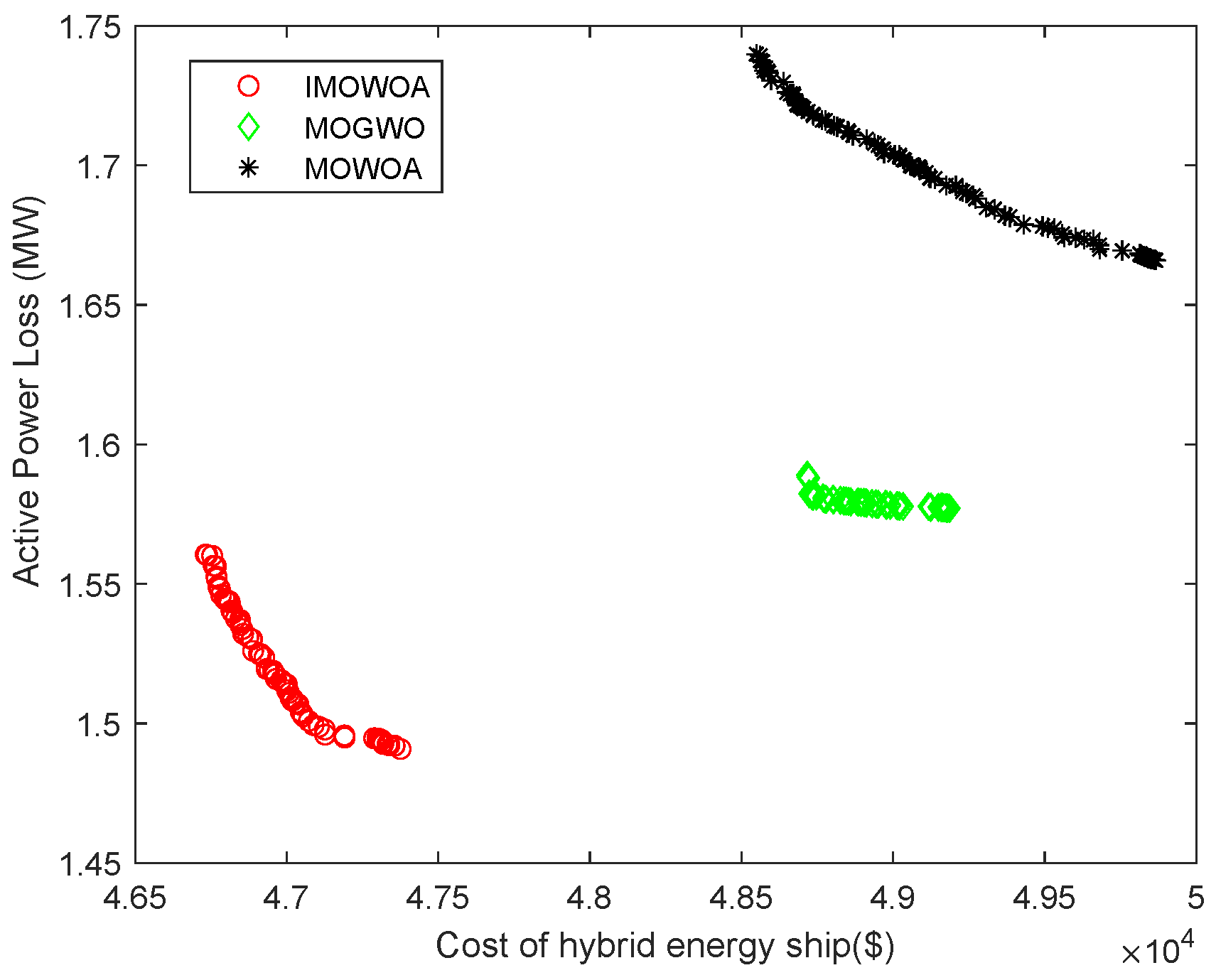
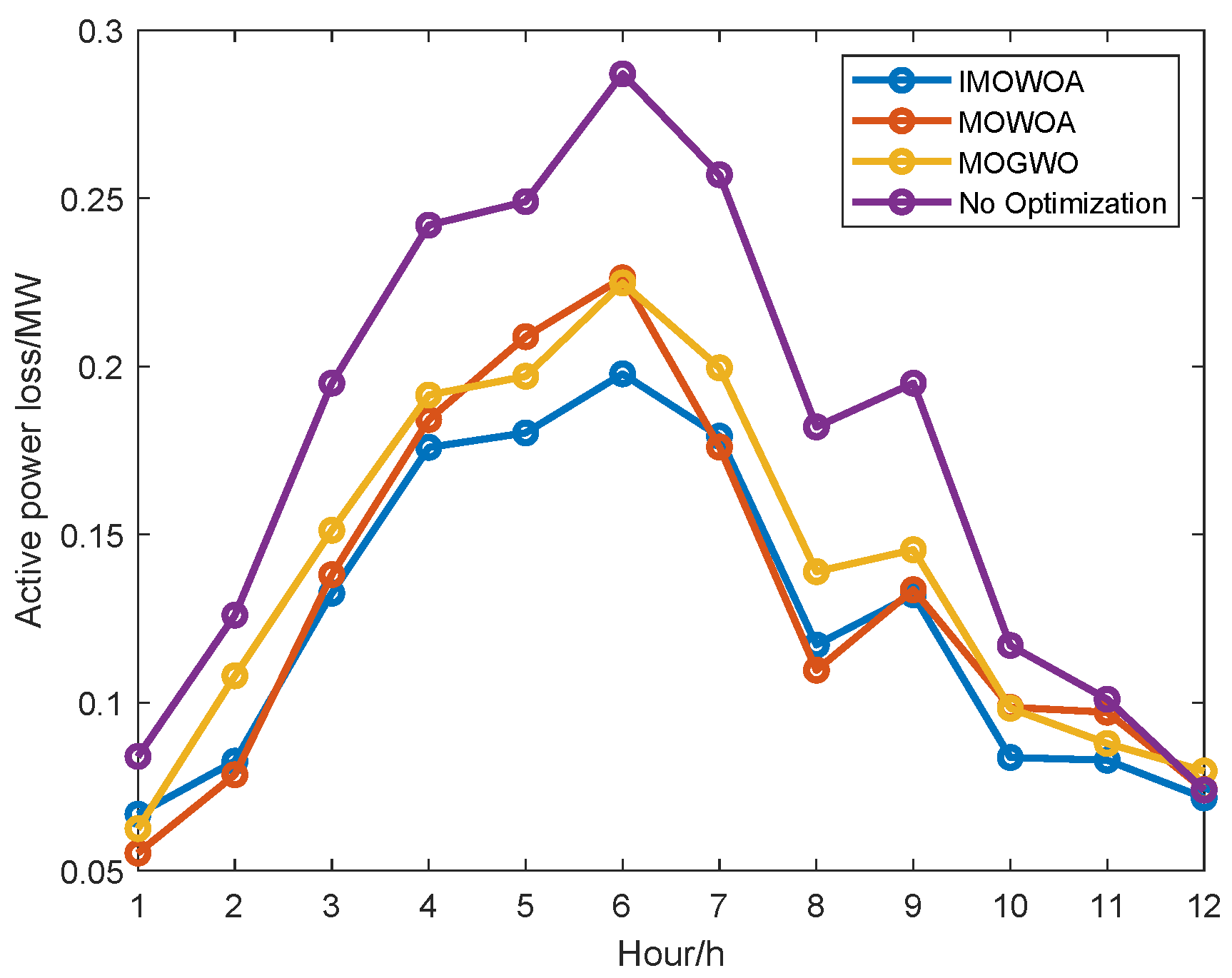
4.3. Performance Analysis of IMOWOA-Based Optimization Model
4.3.1. Performance Test of the IMOWOA
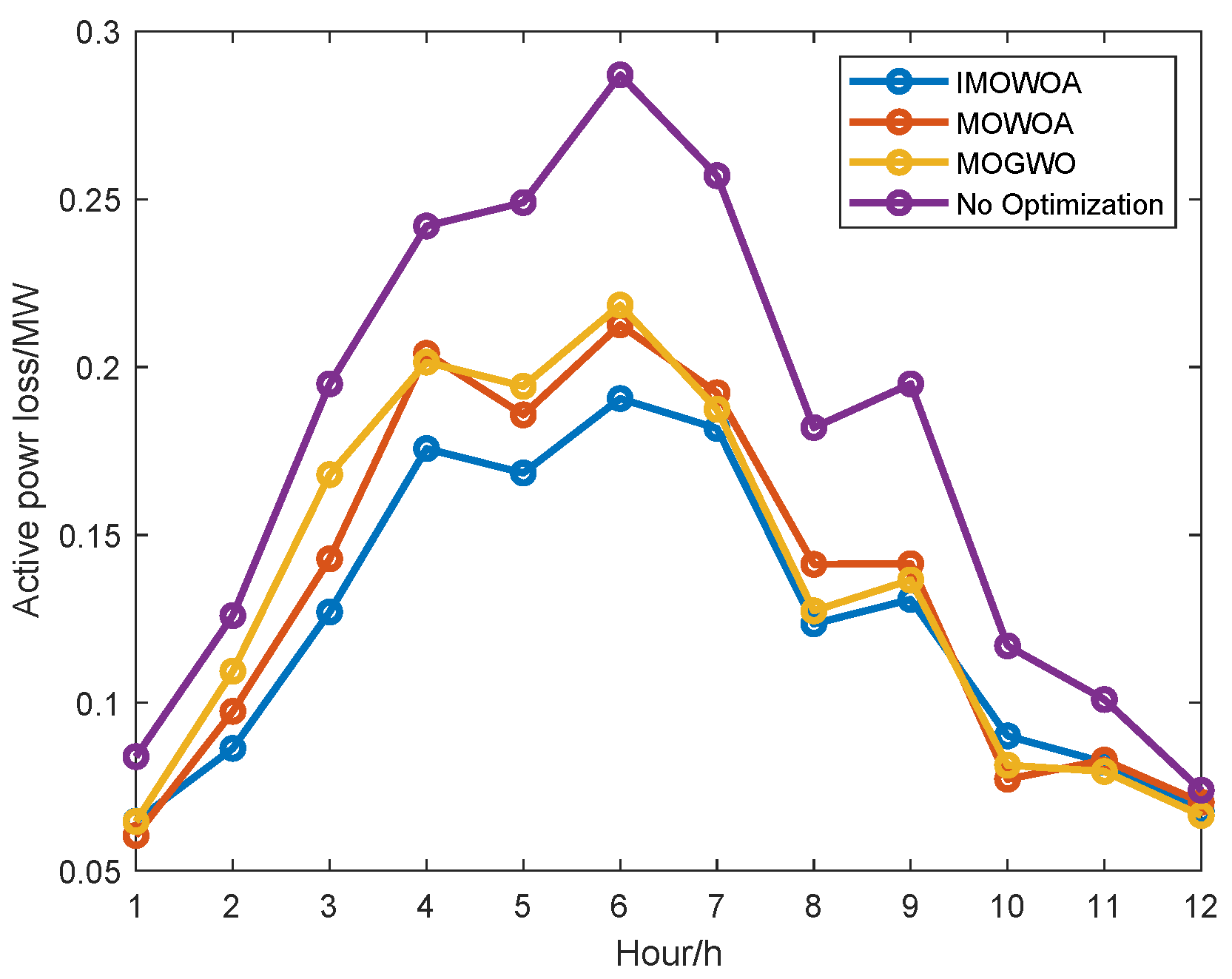
4.3.2. Case 2: Optimal Power Flow Optimization Under Fixed Voyage
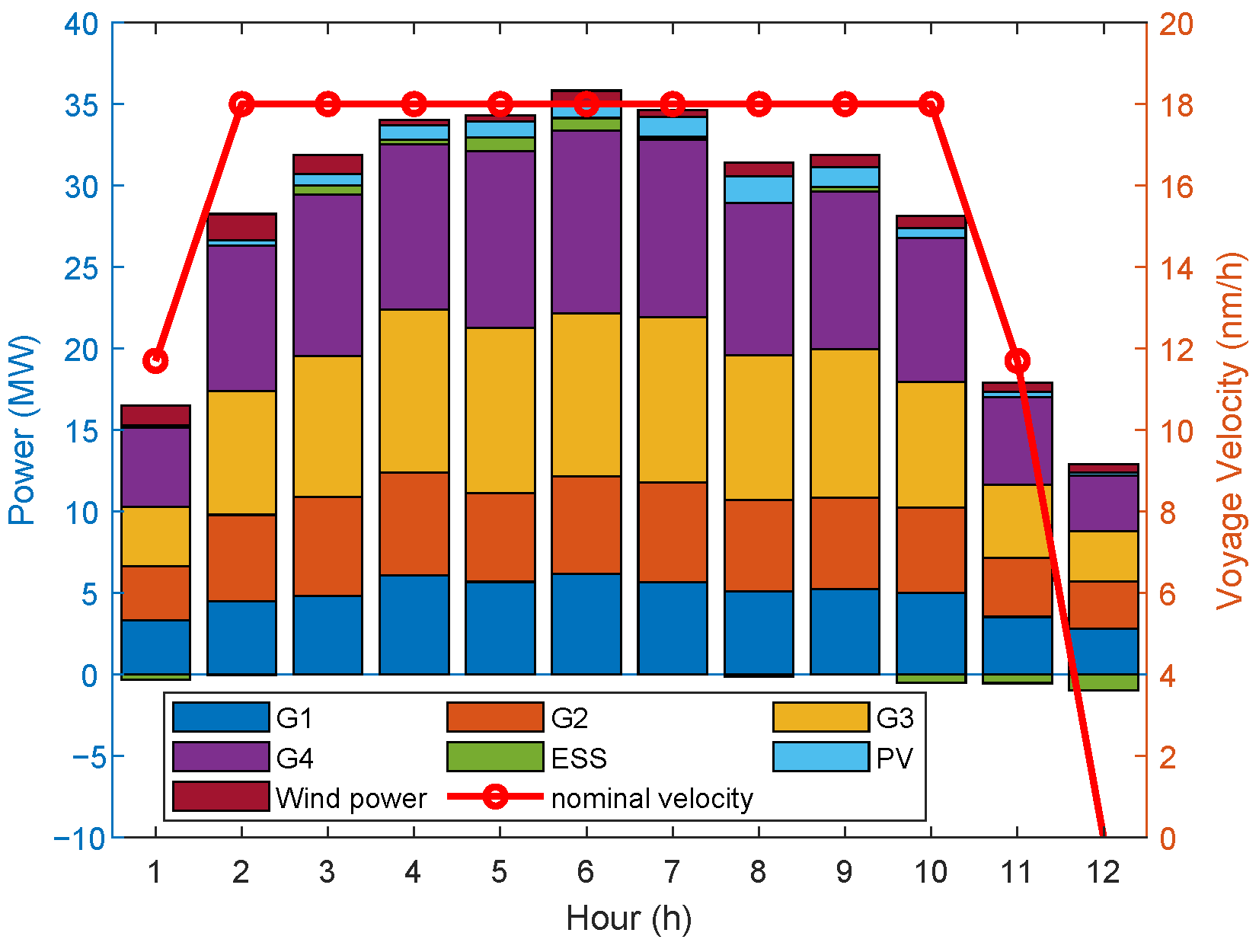
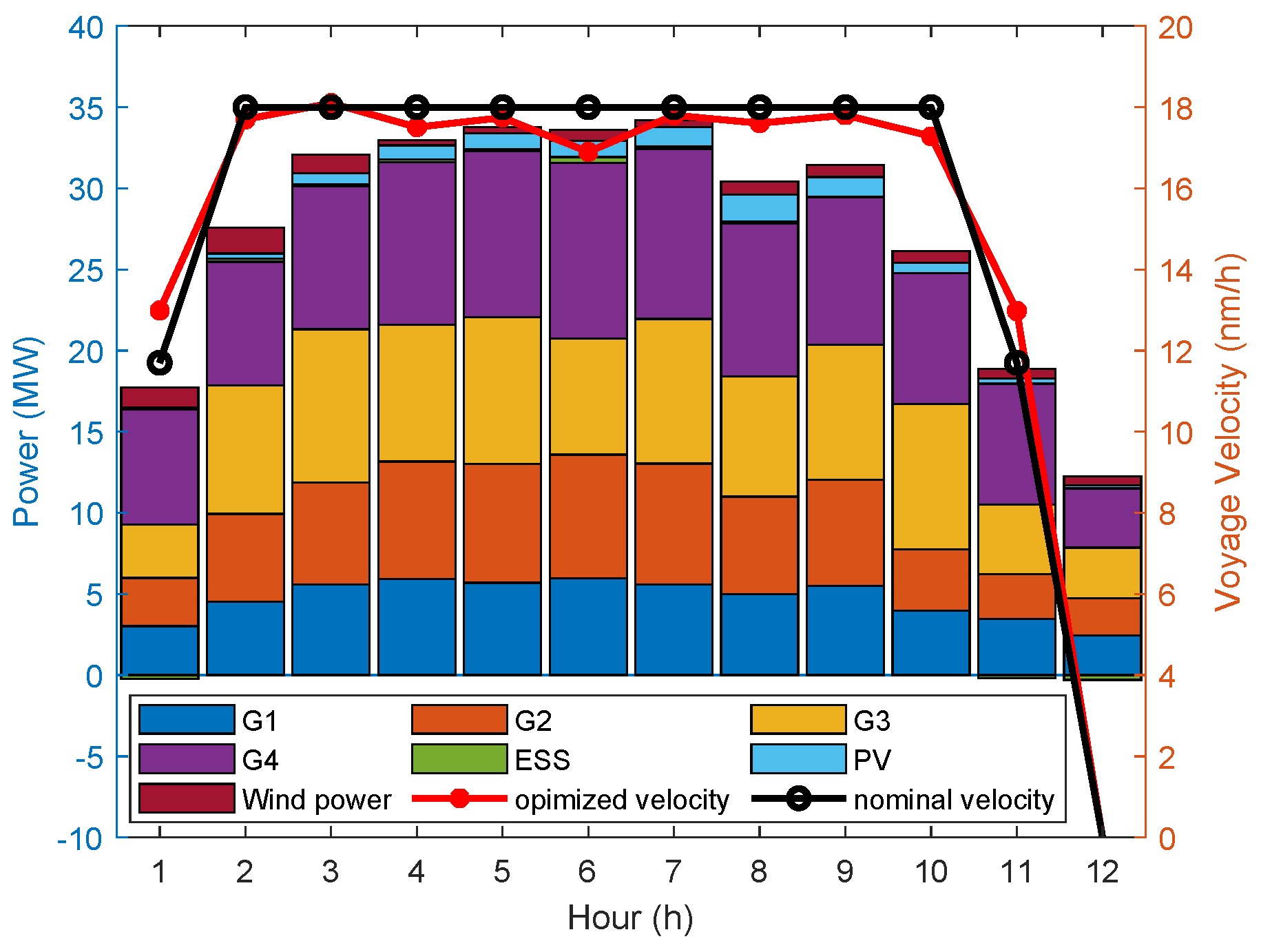
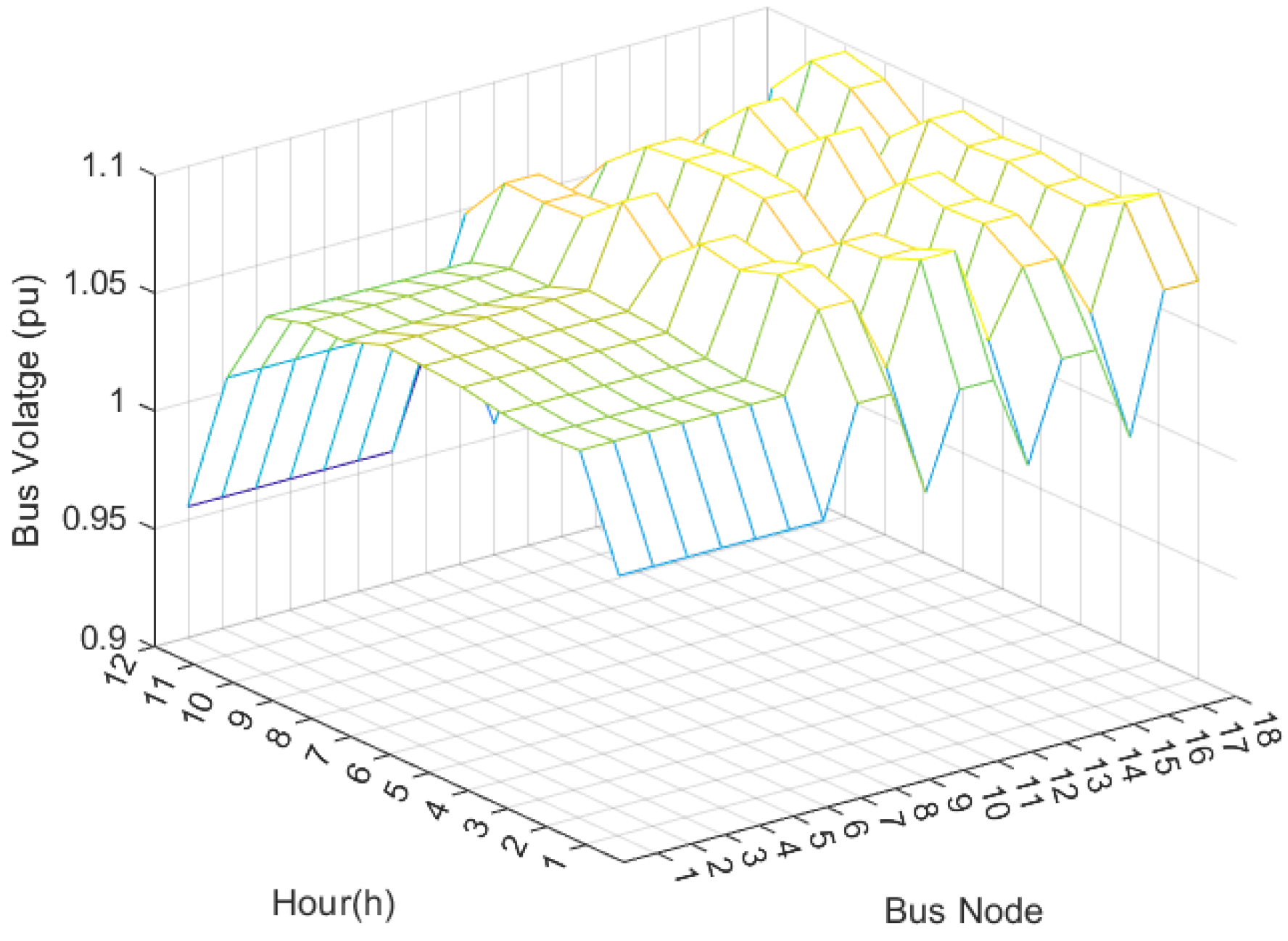
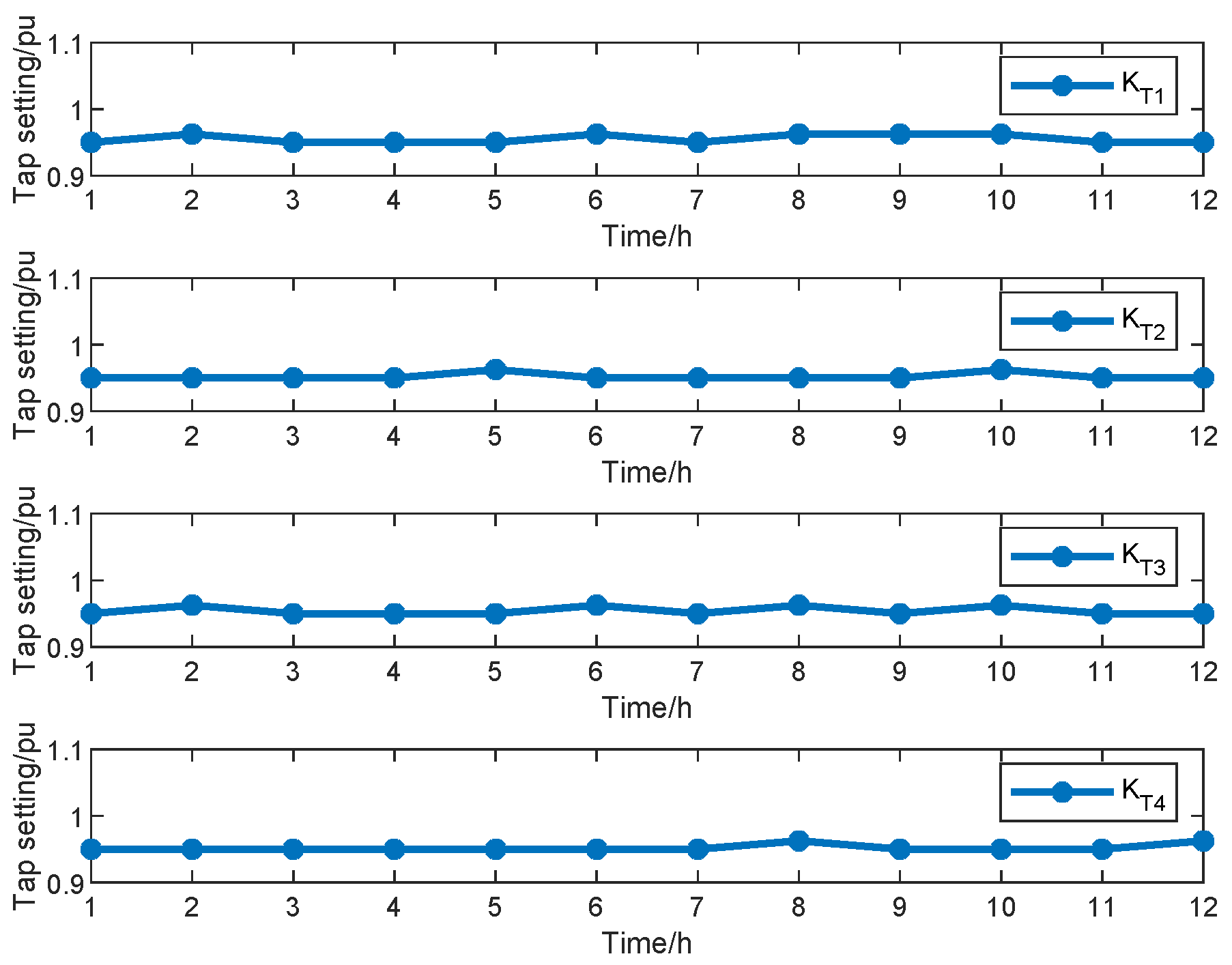
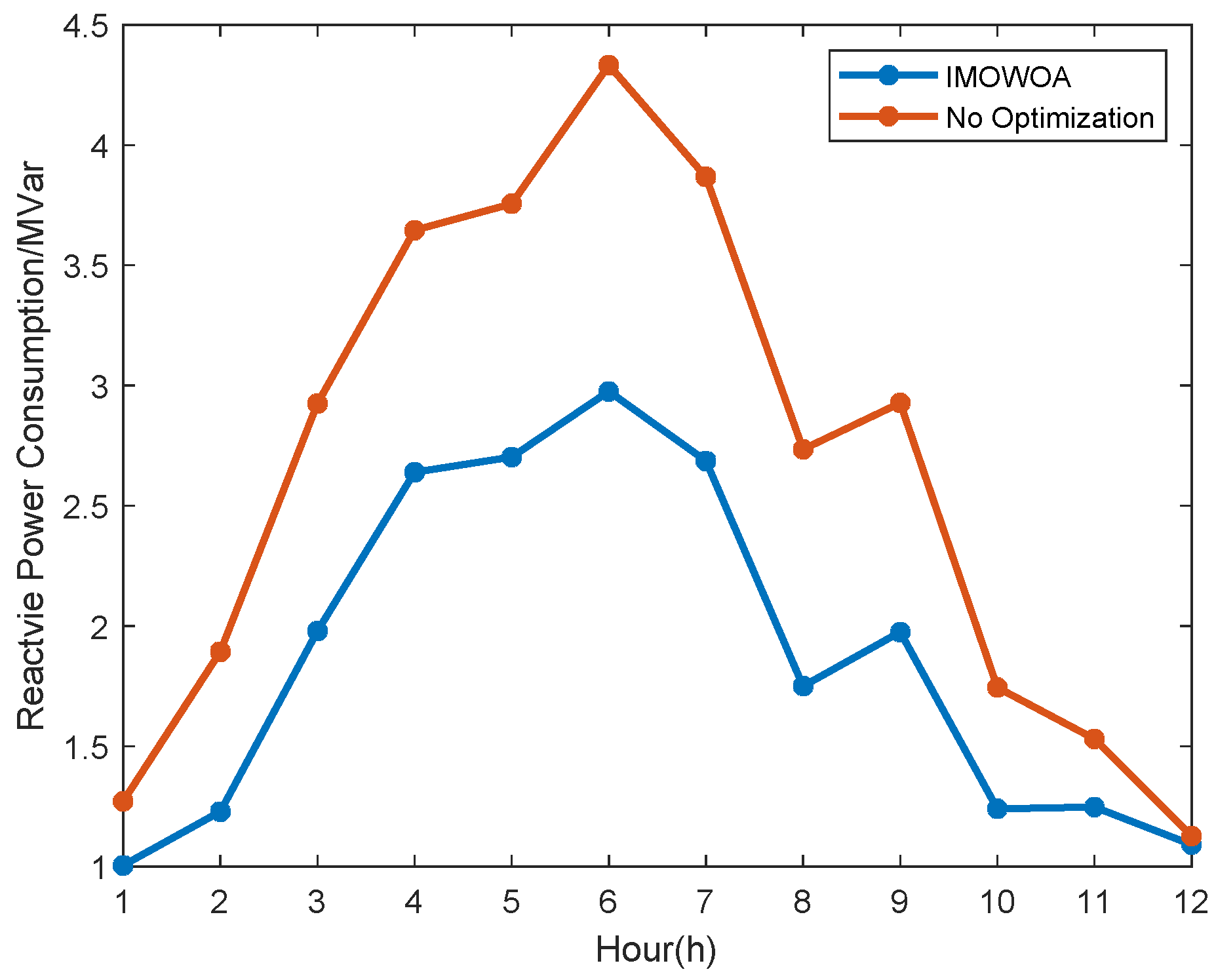
4.3.3. Case 3: Joint Optimization of Voyage and the Optimal Power Flow for HESPS
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Output of the nth | Output of the nth | ||
| ship’s diesel generator at time t | ship’s diesel generator at time t | ||
| , , | Consumption characteristic parameter | Residual energy of the ESS | |
| of the ship’s diesel generator | at time t | ||
| Charging power or the discharging power at time t | , | Charging and discharging rate | |
| Operation cost of the ESS | |||
| Output of PV at time t | Area of the PV | ||
| Total irradiance at time t | Output of the wind power system at time t | ||
| Wind speed of the turbine at time t | Cut-in wind speed of the turbine | ||
| Rated wind speed of the turbine | Removal wind speed of the turbine | ||
| Rated power of the turbine | Ship propulsion power | ||
| Ship speed | , | Ship propulsion load correlation coefficient | |
| Ship operation cost | Number of the generator | ||
| T | Number of hours | Active power loss of the ship | |
| Total number of the branch | k | Branch number | |
| i, j | Bus number | , | Real and imaginary |
| parts in the admittance matrix | |||
| , | Voltage of the bus i, bus j | , | Voltage phase angle of the bus i, bus j |
| Power ramp rate of the generator at the t time | Reactive power of the generator at the t time | ||
| Voltage of the generator at the t time | , | Minimum and maximum | |
| active power output of the generator | |||
| , | Minimum and maximum reactive | , | Minimum and maximum |
| power output of the generator | voltage of the generator i | ||
| Maximum ramp rate of the generator | , | Output of the nth ship’s diesel generator at time t | |
| Power ramp rate of ESS | Maximum power ramp rate of the ESS | ||
| , | Minimum and maximum | , | Minimum and maximum |
| residual energy of the ESS | tap setting of the transformer | ||
| Transformer tap setting at time t | , | Minimum and maximum | |
| reactive power of the shunt VAR compensator | |||
| Reactive power provided | , | Output of the nth ship’s diesel | |
| by the shunt VAR compensator at time t | generator at time t | ||
| Ship velocity at time t | Active power injected | ||
| by the bus i into the network | |||
| Reactive power injected | Phase angle difference | ||
| by the bus i into the network | between the node i and the node j | ||
| mass | Parameter related to | ||
| the ship hull structure and load | |||
| , , | Power factor of each generator |
References
- Han, Y.; Ma, W.; Ma, D. Green maritime: An improved quantum genetic algorithm-based ship speed optimization method considering various emission reduction regulations and strategies. J. Clean. Prod. 2023, 385, 135814. [Google Scholar] [CrossRef]
- Wang, H.; Lang, X.; Mao, W. Voyage optimization combining genetic algorithm and dynamic programming for fuel/emissions reduction. Transp. Res. Part D Transp. Environ. 2021, 90, 102670. [Google Scholar] [CrossRef]
- RESOLUTION MEPC. Amendments to the annex of the protocol of 1997 to amend the international convention for the prevention of pollution from ships, 1973, as modified by the protocol of 1978 relating thereto. Amend. MARPOL Annex VI MEPC 2011, 70, 18. [Google Scholar]
- Fan, A.; Li, Y.; Liu, H.; Yang, L.; Tian, Z.; Li, Y.; Vladimir, N. Development trend and hotspot analysis of ship energy management. J. Clean. Prod. 2023, 389, 135899. [Google Scholar] [CrossRef]
- He, Y.; Mendis, G.J.; Wei, J. Real-time detection of false data injection attacks in smart grid: A deep learning-based intelligent mechanism. IEEE Trans. Smart Grid 2017, 8, 2505–2516. [Google Scholar] [CrossRef]
- James, J.; Hou, Y.; Li, V.O. Online false data injection attack detection with wavelet transform and deep neural networks. IEEE Trans. Ind. Inform. 2018, 14, 3271–3280. [Google Scholar]
- Zhang, G.; Li, J.; Bamisile, O.; Cai, D.; Hu, W.; Huang, Q. Spatio-temporal correlation-based false data injection attack detection using deep convolutional neural network. IEEE Trans. Smart Grid 2021, 13, 750–761. [Google Scholar] [CrossRef]
- Wang, S.; Bi, S.; Zhang, Y.-J.A. Locational detection of the false data injection attack in a smart grid: A multilabel classification approach. IEEE Internet Things J. 2020, 7, 8218–8227. [Google Scholar] [CrossRef]
- Mohammadpourfard, M.; Khalili, A.; Genc, I.; Konstantinou, C. Cyber-resilient smart cities: Detection of malicious attacks in smart grids. Sustain. Cities Soc. 2021, 75, 103116. [Google Scholar] [CrossRef]
- Gao, X.; Yang, X.; Meng, L.; Wang, S. Fast economic dispatch with false data injection attack in electricity-gas cyber–physical system: A data-driven approach. ISA Trans. 2023, 137, 13–22. [Google Scholar] [CrossRef]
- Chen, H.; Wu, H.; Kan, T.; Zhang, J.; Li, H. Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on vmd-gru short-term wind power prediction. Int. J. Electr. Power Energy Syst. 2023, 154, 109420. [Google Scholar] [CrossRef]
- Vu, B.H.; Chung, I.-Y. Optimal generation scheduling and operating reserve management for pv generation using rnn-based forecasting models for stand-alone microgrids. Renew. Energy 2022, 195, 1137–1154. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S.; Lu, X. Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting. Energy 2019, 171, 1053–1065. [Google Scholar] [CrossRef]
- Yu, M.; Niu, D.; Wang, K.; Du, R.; Yu, X.; Sun, L.; Wang, F. Short-term photovoltaic power point-interval forecasting based on double-layer decomposition and woa-bilstm-attention and considering weather classification. Energy 2023, 275, 127348. [Google Scholar] [CrossRef]
- Hein, K.; Xu, Y.; Wilson, G.; Gupta, A.K. Coordinated optimal voyage planning and energy management of all-electric ship with hybrid energy storage system. IEEE Trans. Power Syst. 2020, 36, 2355–2365. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, Q.; Teng, F.; Li, T. Coordinated energy management scheme for ship-harbour energy system based on economic optimal scheduling. In Proceedings of the 2021 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Chengdu, China, 18–20 June 2021; pp. 81–86. [Google Scholar]
- Chen, G.; Liu, D.; Yan, L. Coordinated scheduling and optimal control of all-electric ship energy system based on mixed logical dynamic method. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), IET, Shanghai, China, 24–25 October 2019; pp. 1–7. [Google Scholar]
- Huang, Y.; Lan, H.; Hong, Y.-Y.; Wen, S.; Fang, S. Joint voyage scheduling and economic dispatch for all-electric ships with virtual energy storage systems. Energy 2020, 190, 116268. [Google Scholar] [CrossRef]
- Du, W.; Li, Y.; Shi, J.; Sun, B.; Wang, C.; Zhu, B. Applying an improved particle swarm optimization algorithm to ship energy saving. Energy 2023, 263, 126080. [Google Scholar] [CrossRef]
- Fang, S.; Xu, Y. Multi-objective robust energy management for all-electric shipboard microgrid under uncertain wind and wave. Int. J. Electr. Power Energy Syst. 2020, 117, 105600. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wu, L.; Zheng, X. A risk-averse adaptively stochastic optimization method for multi-energy ship operation under diverse uncertainties. IEEE Trans. Power Syst. 2020, 36, 2149–2161. [Google Scholar] [CrossRef]
- Xu, L.; Wen, Y.; Luo, X.; Lu, Z.; Guan, X. A modified power management algorithm with energy efficiency and ghg emissions limitation for hybrid power ship system. Appl. Energy 2022, 317, 119114. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Fang, S.; Wang, Y.; Zheng, X. Multiobjective coordinated energy dispatch and voyage scheduling for a multienergy ship microgrid. IEEE Trans. Ind. Appl. 2019, 56, 989–999. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, H.; Luo, X.; Chang, S.; Guan, X. A novel optimal dispatch strategy for hybrid energy ship power system based on the improved nsga-ii algorithm. Electr. Power Syst. Res. 2024, 232, 110385. [Google Scholar] [CrossRef]
- Baldwin, T.L.; Lewis, S.A. Distribution load flow methods for shipboard power systems. IEEE Trans. Ind. Appl. 2004, 40, 1183–1190. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, H.; Hong, Y.-Y.; Wen, S.; Yin, H. Optimal generation scheduling for a deep-water semi-submersible drilling platform with uncertain renewable power generation and loads. Energy 2019, 181, 897–907. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, W.; Xu, X.; Liu, H.; Pan, L.; Fan, H.; Zhang, Z.; Chen, Z. Optimal scheduling of a wind energy dominated distribution network via a deep reinforcement learning approach. Renew. Energy 2022, 201, 792–801. [Google Scholar] [CrossRef]
- He, Y.; Gao, Q.; Jin, Y.; Liu, F. Short-term photovoltaic power forecasting method based on convolutional neural network. Energy Rep. 2022, 8, 54–62. [Google Scholar] [CrossRef]
- Houran, M.A.; Bukhari, S.M.S.; Zafar, M.H.; Mansoor, M.; Chen, W. Coa-cnn-lstm: Coati optimization algorithm-based hybrid deep learning model for pv/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Li, H.; Guo, Y. An improved whale optimization algorithm for global optimization and realized volatility prediction. Alex. Eng. J. 2023, 77, 2935–2969. [Google Scholar] [CrossRef]
- Meng, A.-B.; Chen, Y.-C.; Yin, H.; Chen, S.-Z. Crisscross optimization algorithm and its application. Knowl.-Based Syst. 2014, 67, 218–229. [Google Scholar] [CrossRef]
- Wang, W.L.; Li, W.K.; Wang, Z.; Li, L. Opposition-based multi-objective whale optimization algorithm with global grid ranking. Neurocomputing 2019, 341, 41–59. [Google Scholar] [CrossRef]
- Zeng, N.; Song, D.; Li, H.; You, Y.; Liu, Y.; Alsaadi, F.E. A competitive mechanism integrated multi-objective whale optimization algorithm with differential evolution. Neurocomputing 2021, 432, 170–182. [Google Scholar] [CrossRef]
- Li, M.; Xu, G.; Lai, Q.; Chen, J. A chaotic strategy-based quadratic opposition-based learning adaptive variable-speed whale optimization algorithm. Math. Comput. Simul. 2022, 193, 71–99. [Google Scholar] [CrossRef]
- Huang, K.; Li, W.; Gao, F. Barabási-albert model-enhanced genetic algorithm for optimizing LGBM in ship power grid fault diagnosis. Measurement 2025, 249, 116954. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, P.; Sun, F.; Fang, J.; Zhang, C.; Xu, X. Mechanical Fault Diagnosis of High-Voltage Circuit Breakers Based on IPSO-VMD and KFCM-SVM. IEEJ Trans. Electr. Electron. Eng. 2025. [Google Scholar] [CrossRef]
- Arazi, A.; Shapira, E.; Reichart, R. TabSTAR: A Foundation Tabular Model with Semantically Target-Aware Representations. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 19–21 May 2021; Volume 35. [Google Scholar]
- Li, X.; Chen, H.; Xie, F.; Cao, C.; Wang, S.; Shuai, C. Hybrid Model of Multiple Echo State Network Integrated by Evidence Fusion for Fault Diagnosis of a High-Voltage Circuit Breaker. IEEE Trans. Consum. Electron. 2024, 70, 5269–5277. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Kumawat, I.R.; Nanda, S.J.; Maddila, R.K. Multi-objective whale optimization. In Proceedings of the Tencon 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017; Volume 1, pp. 2747–2752. [Google Scholar]




| ESS | PV | Wind Power | |||||
|---|---|---|---|---|---|---|---|
| Minimum power (MW) | 2 | 2 | 3 | 3 | −3 | 0 | 0 |
| Minimum power (MW) | 10 | 10 | 20 | 20 | 3 | 3 | 3 |
| Maximum ramp rate | 5 | 5 | 5 | 5 | 1 | - | - |
| Cost function parameter | = 13 | = 13 | = 5.2 | = 5.2 | = 4.3 | - | - |
| = 12 | = 12 | = 52 | = 5.2 | = 1 | - | - | |
| = 430 | = 430 | = 340 | = 340 | - | - | - | |
| CO2 function parameter | = 13.5 | = 13.5 | = 5.2 | = 5.2 | - | - | - |
| = 10 | = 10 | = 58 | = 58 | - | - | - | |
| = 450 | = 450 | = 390 | = 390 | - | - | - |
| Model | Number of Hidden Layers | Number of Hidden Layer Neurons | Learning Rate | Epoch |
|---|---|---|---|---|
| BP | 2 | layer 1 = 10; layer 2 = 10 | 0.001 | 55 |
| LSTM | 2 | layer 1 = 10; layer 2 = 10 | 0.001 | 55 |
| CNN-LSTM | 2 | CNN: layer 1 = 10; layer 2 = 10 LSTM: layer 1 = 10; layer 2 = 10 | 0.001 | 55 |
| WOA-CNN-LSTM | 2 | CNN: layer 1 = 7; layer 2 = 14 LSTM: layer 1 = 16; layer 2 = 13 | 0.001 | 55 |
| Method | pre | rec | |
|---|---|---|---|
| BP | 0.9788 | 0.9181 | 0.9475 |
| LSTM | 0.9718 | 0.9323 | 0.9516 |
| CNN-LSTM | 0.9624 | 0.9464 | 0.9546 |
| Method in [35] | 0.9812 | 0.9462 | 0.9712 |
| Method in [36] | 0.9723 | 0.9428 | 0.9613 |
| WOA-CNN-LSTM | 0.9864 | 0.9437 | 0.9646 |
| Method | min | max | Average | std |
|---|---|---|---|---|
| BP | 0.9691 | 0.9737 | 0.9720 | 0.0016 |
| LSTM | 0.9703 | 0.9760 | 0.9733 | 0.0018 |
| CNN-LSTM | 0.9708 | 0.9777 | 0.9737 | 0.0022 |
| WOA-CNN-LSTM | 0.9777 | 0.9817 | 0.9800 | 0.0014 |
| Model | Number of Hidden Layers | Number of Hidden Layer Neurons | Learning Rate | Epoch |
|---|---|---|---|---|
| BP | 2 | layer 1 = 10; layer 2 = 10 | 0.01 | 30 |
| LSTM | 2 | layer 1 = 10; layer 2 = 10 | 0.01 | 30 |
| CNN-LSTM | 2 | CNN: layer 1 = 10; layer 2 = 10 LSTM: layer 1 = 10; layer 2 = 10 | 0.01 | 30 |
| WOA-CNN-LSTM | 2 | CNN: layer 1 = 63; layer 2 = 25 LSTM: layer 1 = 29; layer 2 = 31 | 0.0105 | 30 |
| Error Evaluation Index | RMSE | MSE | MAE | |
|---|---|---|---|---|
| LSTM | 0.9504 | 0.1173 | 0.01376 | 0.04983 |
| BP | 0.9379 | 0.1313 | 0.01724 | 0.08152 |
| CNN-LSTM | 0.9579 | 0.1081 | 0.01168 | 0.06864 |
| WOA-CNN-LSTM | 0.9692 | 0.09249 | 0.008553 | 0.04338 |
| Method | min | max | Average | std |
|---|---|---|---|---|
| BP | 0.8972 | 0.9379 | 0.9295 | 0.0123 |
| LSTM | 0.9282 | 0.9504 | 0.9398 | 0.0072 |
| CNN-LSTM | 0.9531 | 0.9579 | 0.9552 | 0.0017 |
| WOA-CNN-LSTM | 0.9676 | 0.9692 | 0.9684 | 0.0004 |
| MOGWO | ||||||
| MOWOA | p = 0.5 | |||||
| IMOWOA | p = 0.5 |
| Test Function | Hypervolume | |||
|---|---|---|---|---|
| MOWOA | MOGWO | IMOWOA | Improvement | |
| ZDT1 | 0.715116 | 0.713204 | 0.717313 | 0.306% |
| ZDT2 | 0.439386 | 0.434151 | 0.442793 | 0.800% |
| ZDT3 | 0.597037 | 0.596749 | 0.599100 | 0.344% |
| Test Function | IGD | |||
| MOWOA | MOGWO | IMOWOA | Improvement | |
| ZDT1 | 0.008446 | 0.008644 | 0.006017 | 28.759% |
| ZDT2 | 0.009478 | 0.009527 | 0.005843 | 38.352% |
| ZDT3 | 0.009977 | 0.010187 | 0.006706 | 32.846% |
| Test Function | SP | |||
| MOWOA | MOGWO | IMOWOA | Improvement | |
| ZDT1 | 0.011305 | 0.010825 | 0.009603 | 15.055% |
| ZDT2 | 0.012565 | 0.012972 | 0.008928 | 28.945% |
| ZDT3 | 0.016242 | 0.013652 | 0.010462 | 35.587% |
| Evaluation Indicator | Cost ($) | Power Loss (MW) | CO2 Emission (kg) | |||
|---|---|---|---|---|---|---|
| Value |
Optimized Proportion | Value |
Optimized Proportion | Value |
Optimized Proportion | |
| No optimization | 52,408.89 | 2.1073 | 55,393.34 | |||
| MOWOA | 48,503.55 | 7.45% | 1.6090 | 23.65% | 51,352.51 | 7.29% |
| MOGWO | 48,550.13 | 7.36% | 1.6090 | 23.65% | 51,858.39 | 6.38% |
| IMOWOA | 47,475.46 | 9.41% | 1.4894 | 29.32% | 50,443.24 | 8.94% |
| Evaluation Indicator | Cost (USD) | Power Loss (MW) | CO2 Emission (kg) | |||
|---|---|---|---|---|---|---|
| Value |
Optimized Proportion | Value |
Optimized Proportion | Value |
Optimized Proportion | |
| No optimization | 52,408.89 | 2.1073 | 55,393.34 | |||
| MOWOA | 48,775.16 | 6.93% | 1.5804 | 25.00% | 51,627.78 | 6.80% |
| MOGWO | 49,307.03 | 7.36% | 1.6849 | 20.04% | 52,125.60 | 5.90% |
| Improved NSGA-II | 48,126.68 | 8.17% | 1.5627 | 25.8% | 51,087.16 | 7.77% |
| IMOWOA | 47,054.75 | 10.22% | 1.5026 | 28.70% | 49,744.14 | 10.20% |
| Evaluation Indicator | Cost ($) | CO2 Emission (kg) | ||
|---|---|---|---|---|
| Value |
Optimized Proportion | Value |
Optimized Proportion | |
| Fixed voyage (case 2) | ||||
| Voyage optimization (case 3) | 47,054.75 | 0.88% | 49,744.14 | 1.39% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Zhu, W.; Chang, S.; Wang, X. Secure Optimization Dispatch Framework with False Data Injection Attack in Hybrid-Energy Ship Power System Under the Constraints of Safety and Economic Efficiency. Electricity 2025, 6, 38. https://doi.org/10.3390/electricity6030038
Luo X, Zhu W, Chang S, Wang X. Secure Optimization Dispatch Framework with False Data Injection Attack in Hybrid-Energy Ship Power System Under the Constraints of Safety and Economic Efficiency. Electricity. 2025; 6(3):38. https://doi.org/10.3390/electricity6030038
Chicago/Turabian StyleLuo, Xiaoyuan, Weisong Zhu, Shaoping Chang, and Xinyu Wang. 2025. "Secure Optimization Dispatch Framework with False Data Injection Attack in Hybrid-Energy Ship Power System Under the Constraints of Safety and Economic Efficiency" Electricity 6, no. 3: 38. https://doi.org/10.3390/electricity6030038
APA StyleLuo, X., Zhu, W., Chang, S., & Wang, X. (2025). Secure Optimization Dispatch Framework with False Data Injection Attack in Hybrid-Energy Ship Power System Under the Constraints of Safety and Economic Efficiency. Electricity, 6(3), 38. https://doi.org/10.3390/electricity6030038







