On the Exact Formulation of the Optimal Phase-Balancing Problem in Three-Phase Unbalanced Networks: Two Alternative Mixed-Integer Nonlinear Programming Models

Abstract

This article presents two novel mixed-integer nonlinear programming (MINLP) formulations in the complex variable domain to address the optimal phase-balancing problem in asymmetric three-phase distribution networks. The first employs a matrix-based load connection model (M-MINLP), while the second uses a compact vector-based representation (V-MINLP). Both integrate the power flow equations through the current injection method, capturing the nonlinearities of Delta and Wye loads. These formulations, solved via an interior-point optimizer and the branch-and-cut method in the Julia software, ensure global optima and computational efficiency. Numerical validations on 8-, 25-, and 37-node feeders showed power loss reductions of 24.34%, 4.16%, and 19.26%, outperforming metaheuristic techniques and convex approximations. The M-MINLP model was 15.6 times faster in the 25-node grid and 2.5 times faster in the 37-node system when compared to the V-MINLP approach. The results demonstrate the robustness and scalability of the proposed methods, particularly in medium and large systems, where current techniques often fail to converge. These formulations advance the state of the art by combining exact mathematical modeling with efficient computation, offering precise, scalable, and practical tools for optimizing power distribution networks. The corresponding validations were performed using Julia (v1.10.2), JuMP (v1.21.1), and AmplNLWriter (v1.2.1).

1. Introduction

1.1. General Context

The operation of electrical distribution systems is a complex task for utility companies, as it is governed by regulatory requirements to ensure a reliable service, maintain high operational quality, and improve energy efficiency [1,2,3]. One of the main challenges in planning and operating these networks is reducing power losses under normal operating conditions, which significantly impacts both economic and environmental aspects [4,5,6,7]. Distribution networks, especially in developing regions, often experience unbalanced load conditions, leading to increased losses and reduced equipment lifespan and service quality [8,9]. Addressing this issue is critical to enhancing the efficiency and sustainability of electricity delivery systems [10,11].

Various strategies have been explored in the literature to minimize power losses, including reactive power compensation through capacitor banks and dynamic compensators [12,13,14,15,16], the integration of renewable energy sources and batteries with variable power factor capabilities [17,18,19,20], distribution feeder reconfiguration [21,22,23], and optimal load balancing [24,25,26], among others. While these methods are effective in reducing power losses, many are costly and require significant investment in equipment and infrastructure, making them less feasible for immediate implementation. In contrast, optimal load balancing constitutes a cost-effective alternative, as it redistributes load connections to balance current flows across phases, requiring minimal investment beyond labor and minor equipment adjustments at coupling points [27,28].

Since it belongs to the family of NP-hard mixed-integer nonlinear programming (MINLP) optimization models [28,29], the main challenge of the optimal load-balancing problem involves finding effective load connections across all the nodes in the network. For this problem, the solution space increases exponentially with the number of nodes (i.e., n as $6^{n-1}$), which implies a billion possible load connection combinations in a medium-sized distribution network [30].

1.2. Literature Review

In the specialized literature, multiple approaches—primarily based on metaheuristic optimizers—have been proposed to solve this complex MINLP problem. Some of these methods are presented below.

In [31], the authors addressed the phase-balancing problem in three-phase distribution networks using a master-slave optimization strategy. In this instance, they proposed an improved version of the Chu and Beasley genetic algorithm (CBGA), integrating adaptive evolution criteria and elements of the vortex search algorithm (VSA) to efficiently explore and exploit the solution space. Their proposal was implemented by combining the improved CBGA in the master stage with a three-phase power flow method based on successive approximations in the slave stage, evaluating phase configurations and the costs of energy losses. The results demonstrated significant reductions in power losses and annual operating costs, with an improvement of 18.79% in the tested networks, outperforming traditional methods while achieving faster processing times.

The authors of [32] developed a demand-side management model based on Rao optimization to address the voltage imbalance issues caused by uneven load distribution across the three phases in electrical distribution networks. This work proposed a method that efficiently redistributes the load in each phase without requiring phase or line reconfiguration. The authors implemented their methodology on the IEEE European 906-bus test system within the MATLAB environment. The results showed a 50% reduction in the voltage imbalance rate and significant decreases in the peak-to-average load ratio across the three phases, with reductions of 6.22%, 38.7%, 3.22%, and 26.46% in the original system.

The work by [27] proposed a load-balancing model for three-phase feeders based on optimized neural networks using smart meters. A hybrid technique was developed, combining feed-forward back-propagation and radial basis function neural networks to optimize the switching sequence of loads while maintaining phase balance. The methodology was implemented in a real case study involving the IDECO power company, utilizing actual consumption data from 27 customers and MATLAB simulations. The results demonstrated that the hybrid technique significantly outperforms individual methodologies, achieving greater load-balancing accuracy and reduced errors in the evaluated metrics.

The authors of [29] presented a load phase balancing method for low-voltage distribution networks that utilizes a genetic algorithm (GA) aimed at minimizing the current imbalance factor and reducing active power losses. This article employed an approach based on smart meter data and evaluated the impact of the number and position of balancing points on the network. The algorithm was implemented on a real distribution grid in northern Romania that featured 68 single-phase consumers. Its performance was compared against that of the particle swarm optimization (PSO) algorithm, providing better balancing solutions and lower energy losses. The results showed a significant loss reduction and improved power supply quality, highlighting the effectiveness of the proposed method for the planning and operation of distribution networks.

The study by [33] outlined a practical method for load balancing in distribution networks that relies on the optimal re-phasing of single-phase customers via a discrete GA. This work introduced an efficient index to evaluate the voltage and current imbalance in four-wire grounded distribution systems. The methodology was implemented on a real 32-node test system located in Bandar Abbas, Iran, analyzing load balancing scenarios, imbalance indices, and practical limitations on the number of re-phased customers. The results demonstrated a significant improvement in energy loss reduction and better voltage and current balance with limited re-phasing, highlighting that minimal changes can have substantial impacts on power supply quality and system efficiency.

In [34], a GA was also used to address the problem of minimizing power losses in unbalanced distribution systems through phase balancing. To validate the methodology, the authors employed a real 47-bus feeder in a rural area of Cambodia, performing MATLAB simulations while considering voltage regulation aspects, the maximum voltage imbalance, and the total power losses. The simulation results confirmed the effectiveness of the proposed method in planning and operating distribution systems. Similarly, in [26], a GA was used to minimize power losses in the IEEE unbalanced 13- and 37-bus systems. The simulation results for these cases were compared based on the minimum power and energy losses obtained.

The authors of [35] developed a hybrid algorithm based on the flower pollination method and fuzzy logic for phase balancing in unbalanced distribution systems, with the main objective of minimizing phase current deviation. Through fuzzy logic, this work integrated multiple objectives, such as voltage regulation of and the reduction in branch current deviation and power losses, into a unified fitness function. The algorithm was implemented on two test systems (a modified version of the IEEE 34-node system and the IEEE 125-node feeder) under different daily load patterns. According to the results, the proposed method significantly reduced the phase current deviation by 96.97% and 98.49% in the 34- and 125-node systems, respectively, outperforming existing techniques and enhancing power supply quality.

Likewise, master-slave strategies have been employed to address this problem. In the master stage, possible load connection configurations are defined via binary or integer modifications, while the slave stage employs a three-phase power flow method to evaluate the impact of said configurations on the expected power losses of a grid. For instance, these master-slave strategies have used the VSA [36], the crow search algorithm (CSA) [37], the hurricane optimization algorithm (HOA) [38], the black hole optimizer (BHO) [39,40], and the salp swarm optimization algorithm (SSA) [41]. These methodologies were validated on 8-, 25-, and 37-node test systems, achieving power loss reductions of over 24%, 4%, and 19%, respectively, in comparison with their base cases.

The main challenge of metaheuristic optimization lies in its tendency to converge to local or near-global optima, given the non-convexities in the solution space. In addition, the stochastic nature of these algorithms can also lead to inconsistent results across simulation runs. This challenge is particularly critical in phase-balancing problems, where the fragmented solution space makes effective navigation and convergence even more difficult.

Other authors have proposed mixed-integer linear or convex approximations to determine optimal load connections by linearizing or neglecting voltage variables. This is the case with the study presented by [24], who developed a mixed-integer linear programming (MILP) model to optimize phase balancing in electrical distribution grids while focusing on minimizing the neutral current, energy losses, and the costs of customer interruption and labor. This model was implemented on Taipower’s LY37 feeder, which serves a mix of industrial and residential customers. The results showed a significant neutral current reduction (i.e., from 93 A to 25 A), an improvement in the average daily energy losses from 2.8% to 1.8%, and a decrease from 7.33% to 2.31% in the voltage imbalance factor. These results validated the effectiveness of the proposed method in improving the reliability and efficiency of distribution networks.

In [42], the authors determined the optimal phase balance to reduce energy losses in distribution networks by comparing three case studies. They implemented a phase balancing technique based on load profiles, evaluating its impact against traditional configurations and methods based on peak load. They used a shortest-path algorithm to calculate the minimum distance from each load to the poles, and load profiles were generated using a bottom-up approach based on survey data. Subsequently, this work employed MILP to define the phase balance in unbalanced three-phase systems. The results indicated that case 3, which incorporated phase balancing based on load profiles, provided the optimal radial topology, achieving a significant energy loss reduction. There are other instances in the literature, like the ones presented by [30,43], whose aim was to relax the constraints associated with the problem in order to make the solution space convex.

However, the effectiveness of these approaches always depends on the grid’s topology and the equivalent objective function implemented, meaning that most of them, even convex ones, only reach local optima when evaluated in the exact MINLP model.

1.3. Novelty and Main Contributions

The state of the art highlights two main approaches for addressing the optimal phase-balancing problem in asymmetric three-phase distribution networks. On the one hand, metaheuristic techniques have been widely employed due to their ability to handle complex problems such as MINLP models. Strategies like GAs, PSO, and the VSA, as well as hybrid methods incorporating fuzzy logic and artificial intelligence, have proven effective in exploring large solution spaces and finding near-global optima. However, these methodologies often face challenges such as convergence to local optima and inconsistencies in their results due to the stochastic nature of their search processes. On the other hand, linear or convex approximations have emerged as an alternative to simplify the problem by relaxing the nonlinearities associated with load configurations and the power flow equations. These techniques, based on MILP or convex transformations, allow for faster and more manageable solutions, albeit with limitations in the accuracy of the results. Although these approximations can produce valid solutions for specific configurations, their dependence on network topology and the simplifications made may hinder their ability to find the true global optimum. Both approaches exhibit opportunities and limitations, underscoring the need for more robust and exact methods to overcome these challenges.

In this vein, the novelty of this work lies in the mathematical formulation of two exact models to address the optimal phase-balancing problem in asymmetric three-phase distribution networks while ensuring a globally optimal solution. Unlike the literature-reported methodologies, which typically rely on metaheuristic algorithms or linear/convex approximations to model and solve the problem but often become trapped in local optima, this study provides a mathematical formulation for the problem in the complex variable domain. This approach simplifies mathematical expressions by avoiding the decomposition of variables into real and imaginary components, thereby reducing the problem’s size and the number of equations. Our method directly handles properties such as impedance and admittance, facilitates common operations in electrical systems, and offers a more intuitive physical interpretation of magnitudes and angles. Furthermore, it is compatible with advanced numerical methods and optimization solvers, enhancing computational efficiency while enabling a more direct implementation in specialized software. Additionally, this study introduces a novel approach based on matrix and vector representations to analyze all possible load connection configurations. Numerical validations demonstrated that these formulations outperform the existing methodologies, finding the global optimum of the problem.

Our primary contributions, which underscore the novelty of this research, are detailed below:

• Two MINLP formulations are proposed for phase balancing, which are modeled in the domain of complex variables and integrate the power flow equations through the current injection method. These formulations capture the nonlinearities of the problem more accurately, surpassing the approximations used in previous studies.
• Two distinct approaches are introduced to represent load connection configurations: a matrix-based formulation that considers all possible permutations (e.g., from ABC to BAC) and a more compact vector-based representation, offering flexibility and precision in modeling.
• The models were solved using an interior-point optimizer combined with the branch-and-cut algorithm in the Julia software. Numerical tests on 8-, 25-, and 37-node feeders demonstrated significant improvements compared to the literature-reported metaheuristic methodologies in terms of both accuracy and computational efficiency.

The source code utilized to solve the proposed M-MINLP and V-MINLP formulations has been made publicly available in a dedicated repository. This repository contains the Julia scripts, the test system data, and instructions for reproducing the results presented herein. The repository can be accessed at https://github.com/odmontoya/Phase-balancing-for-3phase-networks (accessed on 4 December 2024).

1.4. Document Structure

The remainder of this document is organized as follows. Section 2 presents the general power flow model for three-phase networks using the current injection model. Section 3 describes the first MINLP model using the matrix variable representation, while Section 4 presents the second MINLP model via a vector variable representation. Section 5 outlines the methodology used to solve the optimal phase-balancing problem. Section 6 describes the main characteristics of the 8-, 25-, and 37-bus grids used in this study, in addition to numerical validations and comparisons with literature reports. Finally, Section 7 lists the main concluding remarks, as well as some possible future works.

2. General Three-Phase Power Flow Formulation

The optimal phase-balancing problem for three-phase asymmetric networks can be represented as a MINLP model. Its main goal is to define the optimal load connection at each node in order to reduce the expected power losses in all the branches of the grid. This optimization problem includes binary variables representing possible load connections, as well as continuous ones related to the power flow equations, such as voltage and complex power generation, among others. Most of the equations presented in this study are original developments derived from fundamental circuit laws, such as Kirchhoff’s laws and the relationships between impedance, current, and voltage in three-phase systems. These equations are essential for accurately modeling the nonlinearities associated with Delta and Wye load configurations. The optimization process aims to minimize active power losses, with decision variables representing the optimal load connections at each node.

2.1. Objective Function

The main goal of re-phasing load connections in three-phase nodes is to minimize the expected grid power losses (i.e., $p_{loss}$) associated with heat dissipation in conductors. This objective function can be modeled as shown in Equation (1):

$$\begin{array}{c}\hfill min{p}_{loss}=\mathrm{Re}\left\{\sum _{j\in \mathbf{L}}{\mathbb{V}}_{j3\phi }^{\top }{\mathbb{I}}_{j3\phi }^{★}\right\},\end{array}$$

(1)

where ${\mathbb{V}}_{j3\phi }$ represents the three-phase voltage drop at line j, and ${\mathbb{I}}_{j3\phi }$ denotes the three-phase current flow of line j. Note that $\mathbf{L}$ is the set containing all the three-phase distribution lines. These quantities are defined in the phase domain and explicitly account for asymmetries in unbalanced three-phase networks. The distribution of currents across the system depends on the phase assignment of the loads, which is determined by the binary phase-selection variables. Consequently, optimizing phase configuration directly influences power losses by modifying current magnitudes and balancing conditions.

2.2. Power Flow Equations

Kirchhoff’s current law must be explicitly used for each node to represent the nodal power equilibrium in the phase-balancing problem. This can be achieved with the aid of the node-to-branch incidence matrix, as presented in Equation (2):

$$\begin{array}{c}\hfill {\mathbb{I}}_{k3\phi }^g-{\mathbb{I}}_{k3\phi }^d\left(x\right)=\sum _{j\in \mathbf{L}}{\mathcal{A}}_{kj3\phi }{\mathbb{I}}_{j3\phi },\left\{k\in \mathbf{N}\right\}\end{array}$$

(2)

where ${\mathbb{I}}_{k3\phi }^g$ represents the three-phase current injection by a power source connected at bus k; ${\mathbb{I}}_{k3\phi }^d\left(x\right)$ corresponds to the current consumption at bus k, which is a function of the connected load, defined generically by the binary variable x; ${\mathcal{A}}_{kj3\phi }$ is the component of the node-to-branch incidence matrix that relates bus k to line j; and $\mathbf{N}$ is the set containing the three-phase grid nodes. The impact of phase selection is incorporated through the rotation matrix that modifies load currents according to the assigned phase configuration. This, in turn, affects the current balance at each node and subsequently alters the current flows in the system’s lines, thereby influencing power losses.

2.3. Line Voltage Drop

The voltage drop at each distribution line j that connects nodes k and m can be defined as a function of the three-phase branch impedance ${\mathbb{Z}}_{j3\phi }$, as presented in Equation (3).

$$\begin{array}{c}\hfill {\mathbb{V}}_{j3\phi }=\sum _{k\in \mathbf{N}}{\mathcal{A}}_{kj3\phi }{\mathbb{V}}_{k3\phi }={\mathbb{Z}}_{j3\phi }{\mathbb{I}}_{j3\phi }.\left\{j\in \mathbf{J}\right\}\end{array}$$

(3)

2.4. Load Current

The current demand at each node k is influenced by the specific load connection type. For three-phase grids, loads can be connected in either a triangle ($\Delta$) or a Wye (Y) configuration. Furthermore, in the presence of constant power loads, the relationship between voltage and current is governed by a hyperbolic nonlinear equation, as described in (5) and (6) [44]. For a general three-phase load ${\mathbb{S}}_{k3\phi }={\mathbb{S}}_{k3\phi }^Y+{\mathbb{S}}_{k3\phi }^{\Delta }$, the demanded current ${\mathbb{I}}_{k3\phi }^d\left(x\right)$ can be defined as shown in Equation (4):

$$\begin{array}{cc}\hfill {\mathbb{I}}_{k3\phi }^d\left(x\right)& ={\mathbb{I}}_{k3\phi }^{\Delta }\left(x\right)+{\mathbb{I}}_{k3\phi }^Y\left(x\right),\left\{k\in \mathbf{N}\right\}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\mathbb{I}}_{k3\phi }^Y\left(x\right)& ={\mathbf{diag}}^{-1}\left({\mathbb{V}}_{k3\phi }^{★}\right){\mathbb{S}}_{k3\phi }^{Y,★}\left(x\right),\left\{k\in \mathbf{N}\right\}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathbb{I}}_{k3\phi }^{\Delta }\left(x\right)& ={\mathcal{M}}^{\top }\left({\mathbf{diag}}^{-1}\left(\mathcal{M}{\mathbb{V}}_{k3\phi }^{★}\right)\right){\mathbb{S}}_{k3\phi }^{\Delta ,★}\left(x\right),\left\{k\in \mathbf{N}\right\}\hfill \end{array}$$

(6)

In this context, it is evident that the three-phase constant power loads (i.e., ${\mathbb{S}}_{k3\phi }^Y$ and ${\mathbb{S}}_{k3\phi }^{\Delta }$) are defined by the decision variable x. Furthermore, $\mathcal{M}$ is a transformation matrix used to convert triangle loads into Wye ones in order to calculate the current demand. This transformation matrix is defined in Equation (7).

$$\begin{array}{c}\hfill \mathcal{M}=\left[\begin{array}{ccc}1& -1& 0\\ 0& 1& -1\\ -1& 0& 1\end{array}\right].\end{array}$$

(7)

2.5. Voltage Regulation

Constraint (8) represents the voltage regulation of a distribution system. Here, the voltage magnitude at node k must remain within limits predefined by the network operator.

$$V^{min}\le \left|{\mathbb{V}}_{k3\phi }\right|\le V^{max},\left\{k\in \mathbf{N}\right\},$$

(8)

where $V^{min}$ and $V^{max}$ represent the minimum and maximum voltage regulation limits established by the network operator’s regulatory policies.

Note that the mathematical model defined from (1) to (8) can be extended to incorporate the presence of distributed generation (DG) in unbalanced three-phase distribution networks. To this effect, the formulation would need to include additional constraints that account for the contribution of DG units to the network’s power balance. Specifically, the nodal current balance (Equation (2)) should be updated to include the current injected by DGs. This modification would require defining an additional constraint to compute the injected current based on the complex power output of the DG units, similar to the approach used in Equation (5). Furthermore, an additional constraint should be introduced to establish the generation limits of these devices, ensuring that the optimization process respects their operational constraints. By incorporating these adjustments, the model could effectively optimize phase balancing while considering the impact of DG, making it applicable to modern active distribution networks.

Remark 1.

The two proposed models for optimal load balancing in three-phase networks use two alternative ways to define the decision variable x: one involves a matrix structure and the other employs a vector representation.

3. Matrix MINLP Formulation

In three-phase distribution grids, there are six possible load connections per node, three in positive sequence and three in negative sequence [45]. These load connection possibilities are defined in

Table 1. Possible load connections applicable to each node of the network.

Con.	Rotation Matrix	Con.	Rotation Matrix
ABC (+)	${\mathcal{R}}_1=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$	ACB (−)	${\mathcal{R}}_4=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]$
BCA (+)	${\mathcal{R}}_2=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]$	CBA (−)	${\mathcal{R}}_5=\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]$
CAB (+)	${\mathcal{R}}_3=\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]$	BAC (−)	${\mathcal{R}}_6=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$

. The load rotation matrix outlines the relationship between the initial and final loads of each phase within each sequence.

Note that the rotation matrix defines a matrix of variables $x_{kfg}$ that associates the load connection at bus k with phases f and g. This is in turn defined in the set of phases $\mathbf{P}=\left\{a,b,c\right\}$. For simplicity, in this formulation, the load connection type (i.e., triangle or Wye) is neglected, generally expressing the initial three-phase load ${\mathbb{S}}_{k3\phi }^0={\left[{\mathbb{S}}_{ka}{\mathbb{S}}_{kb}{\mathbb{S}}_{kc}\right]}^{\top }$. To determine the final load connection (i.e., ${\mathbb{S}}_{k3\phi }^1$), the linear constraint presented in Equation (9) is used.

$$\begin{array}{c}\hfill {\mathbb{S}}_{kf3\phi }^1=\sum _{g\in \mathbf{P}}{x}_{kfg}{\mathbb{S}}_{kg3\phi }^0.\left\{k\in \mathbf{N},f\in \mathbf{P}\right\}\end{array}$$

(9)

In addition, considering the structure of the rotation matrix in Table 1, two linear constraints can be assigned to the decision variable $x_{kfg}$, as presented in Equations (10) and (11).

$$\begin{array}{c}\hfill \sum _{f\in \mathbf{P}}{x}_{kfg}=1,\left\{k\in \mathbf{N},g\in \mathbf{P}\right\},\end{array}$$

(10)

$$\begin{array}{c}\hfill \sum _{g\in \mathbf{P}}{x}_{kfg}=1,\left\{k\in \mathbf{N},f\in \mathbf{P}\right\}.\end{array}$$

(11)

Remark 2.

The first MINLP model was defined from (1) to (11) using a matrix variable representation to specify the possible load connections of each node.

4. Vector MINLP Formulation

An alternative formulation for the phase-balancing problem considers the rotation matrix in Table 1 as a constant input for the optimization model. This is carried out through ${\mathcal{R}}_c$, where c is a subscript for the set of possible load connections $\mathbf{C}$. In the vector formulation, the decision variable is defined as $x_{kc}$, which in turn allows defining the load connection for each node as shown in Equation (12).

$$\begin{array}{c}\hfill {\mathbb{S}}_{k3\phi }^1=\left(\sum _{c\in \mathbf{C}}{x}_{kc}{\mathcal{R}}_c\right){\mathbb{S}}_{k3\phi }^0.\left\{k\in \mathbf{N}\right\}\end{array}$$

(12)

The linear constraint shown in Equation (13) is added to the decision variable in order to ensure that one possible load connection can be assigned to each node.

$$\begin{array}{c}\hfill \sum _{c\in \mathbf{C}}{x}_{kc}=1.\left\{k\in \mathbf{N}\right\}\end{array}$$

(13)

Remark 3.

The second MINLP model is defined from (1) to (8) and includes Equations (12) and (13). This optimization model uses a vector representation to specify the possible load connections of each node.

5. Methodology: Julia Implementation

Julia is a high-performance programming language specifically designed to address computationally intensive problems such as those involving mathematical optimization [46]. This study used Julia in combination with the JuMP package to model and solve the optimal phase-balancing problem in unbalanced three-phase distribution networks. JuMP is a specialized package for formulating optimization models that is capable of handling a wide variety of problem types, including linear, nonlinear, and mixed-integer programming models [47]. This tool was selected for its flexibility and efficiency in solving large-scale problems, in addition to its ability to integrate multiple solvers optimized for different types of problems [48,49,50,51,52,53,54].

The mathematical models proposed for phase balancing; the matrix-based model described in Equations (1)–(11); and the vector-based model in (1)–(7), (12), and (13) were solved using BONMIN [55]. This solver is suitable for addressing problems involving continuous and discrete variables, as well as nonlinear models with non-convex constraints. BONMIN combines solution techniques for MINLP and nonlinear programming (NLP) models, primarily employing a branch-and-bound strategy that integrates methods to solve NLP subproblems at each node of the tree [55], e.g., the Ipopt solver, which is based on the interior-point method [46,56]. Additionally, BONMIN allows using approaches such as B-BB (basic branch-and-bound), B-Hyb (hybrid), and B-OA (outer approximation), adapting to the specific characteristics of the problem [57,58]. These tools make BONMIN a robust choice for solving MINLP models, ensuring optimal or near-optimal solutions to high-complexity problems such as that studied herein.

Figure 1 illustrates the decision-making process used to evaluate load connection configurations and verify operational constraints. The modular structure ensures that the methodology is applicable to both the matrix- and the vector-based formulations. This design facilitates generalization to other optimization techniques and provides a clear representation of the steps involved, including the decision points for selecting optimal solutions.

Below are the steps for obtaining an exact solution to the MINLP models using Julia and JuMP, presented in tutorial form:

• Input the parametric information of the test system: Enter the necessary system data, such as the total number of nodes in the distribution network, the active and reactive power consumption of each load per phase, the connection type of each node (Delta or Wye), the impedance matrices of the distribution lines, and the connections between nodes (system topology). Additionally, ensure that the data are compatible with the format required for implementing the optimization model.
• Define the optimization model: Create an optimization model using the BONMIN solver. This model must be designed to handle the characteristics of the problem, i.e., continuous and binary variables and the non-convex constraints associated with optimal phase balancing.
• Create the optimization variables: The representative optimization variables necessary for implementing Equations (1)–(13) must be defined. This includes the three-phase voltages (${\mathbb{V}}_{j3\phi }$ and ${\mathbb{V}}_{k3\phi }$), the three-phase current at the slack node (${\mathbb{I}}_{k3\phi }^g$), the three-phase currents of the loads (${\mathbb{S}}_{k3\phi }^Y$ and ${\mathbb{S}}_{k3\phi }^{\Delta }$), and the binary decision variables ($x_{kfg}$ for the matrix model) and ($x_{kc}$ for the vector model).
• Implement the optimization problem: Define all the necessary constraints for the mathematical model, such as those related to the current balance and the binary variables. For the matrix-based model, implement Equations (2)–(11), and, for the vector-based model, include Equations (2)–(7) as well as (12) and (13). Note that these constraints reflect the structural differences between the models.
• Define the objective function: Establish the objective function, which, in this case, is to minimize the active power losses in the distribution system, as presented in Equation (1).
• Solve the optimization model: Run BONMIN to solve the model. Properly configure the solver parameters, such as the iteration limits, numerical tolerance, and branching and cutting strategies, in order to ensure convergence and efficiency in the solution process.
• Extract and analyze the results: Once the model has been solved, the new connection configurations of the nodes can be determined, i.e., from the six configurations presented in Table 1, the final connection of each load can be identified. Additionally, the resulting voltages and currents of the system can be evaluated, and the total power losses can be calculated and compared against the initial conditions in order to validate the effectiveness of the proposed methodology.

6. Computational Analysis and Validation

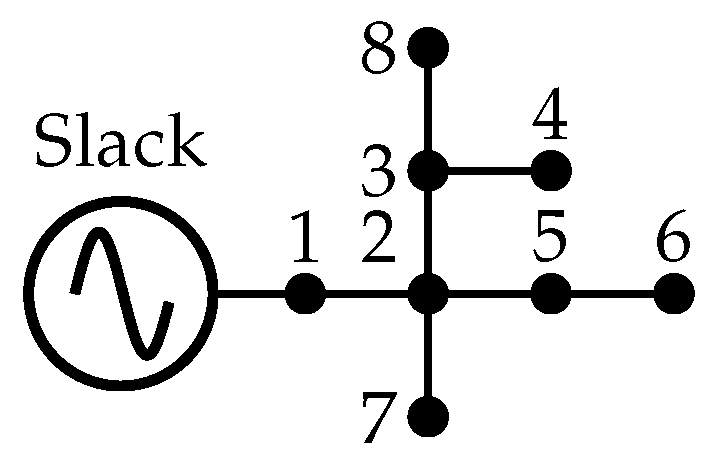
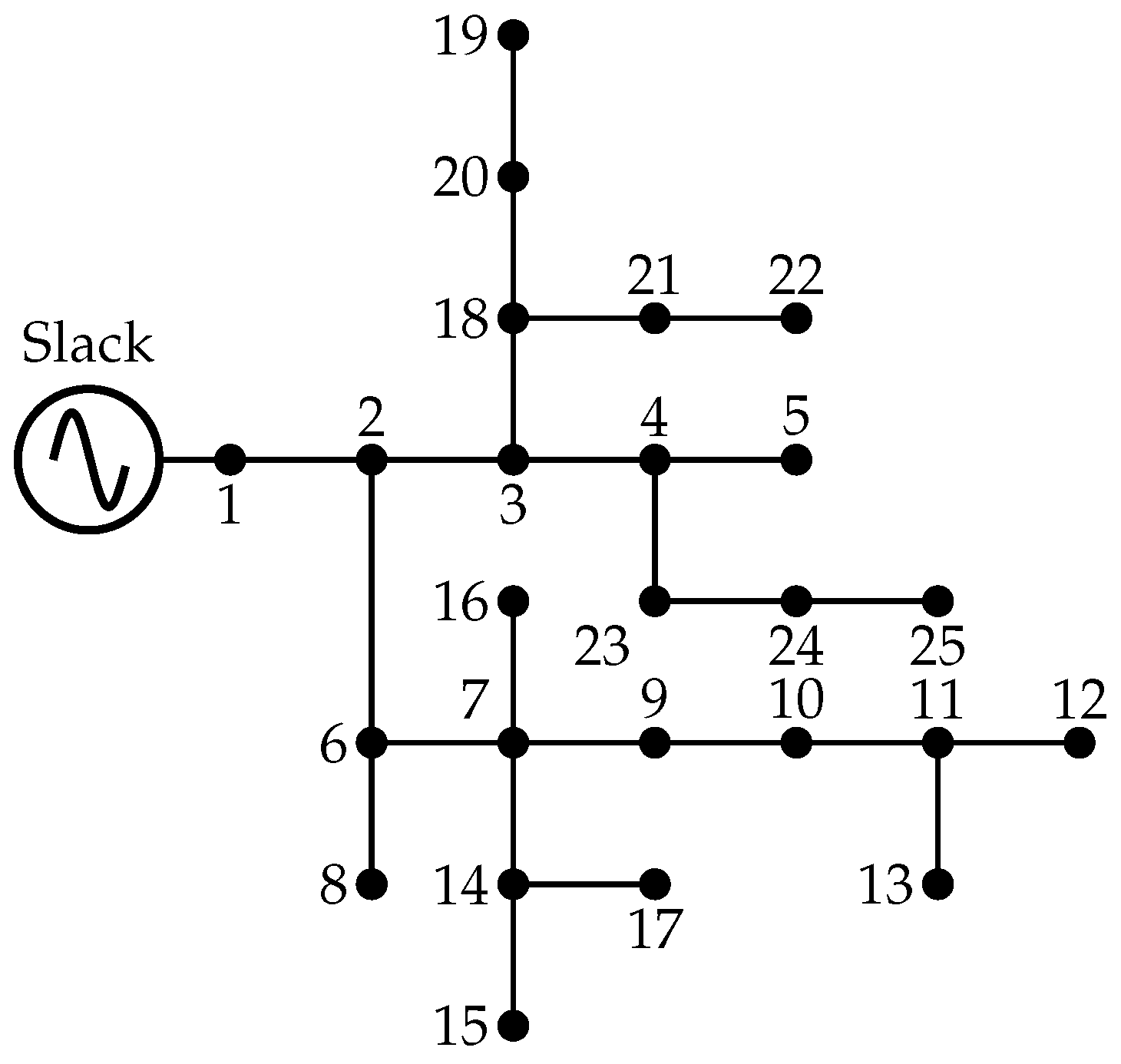
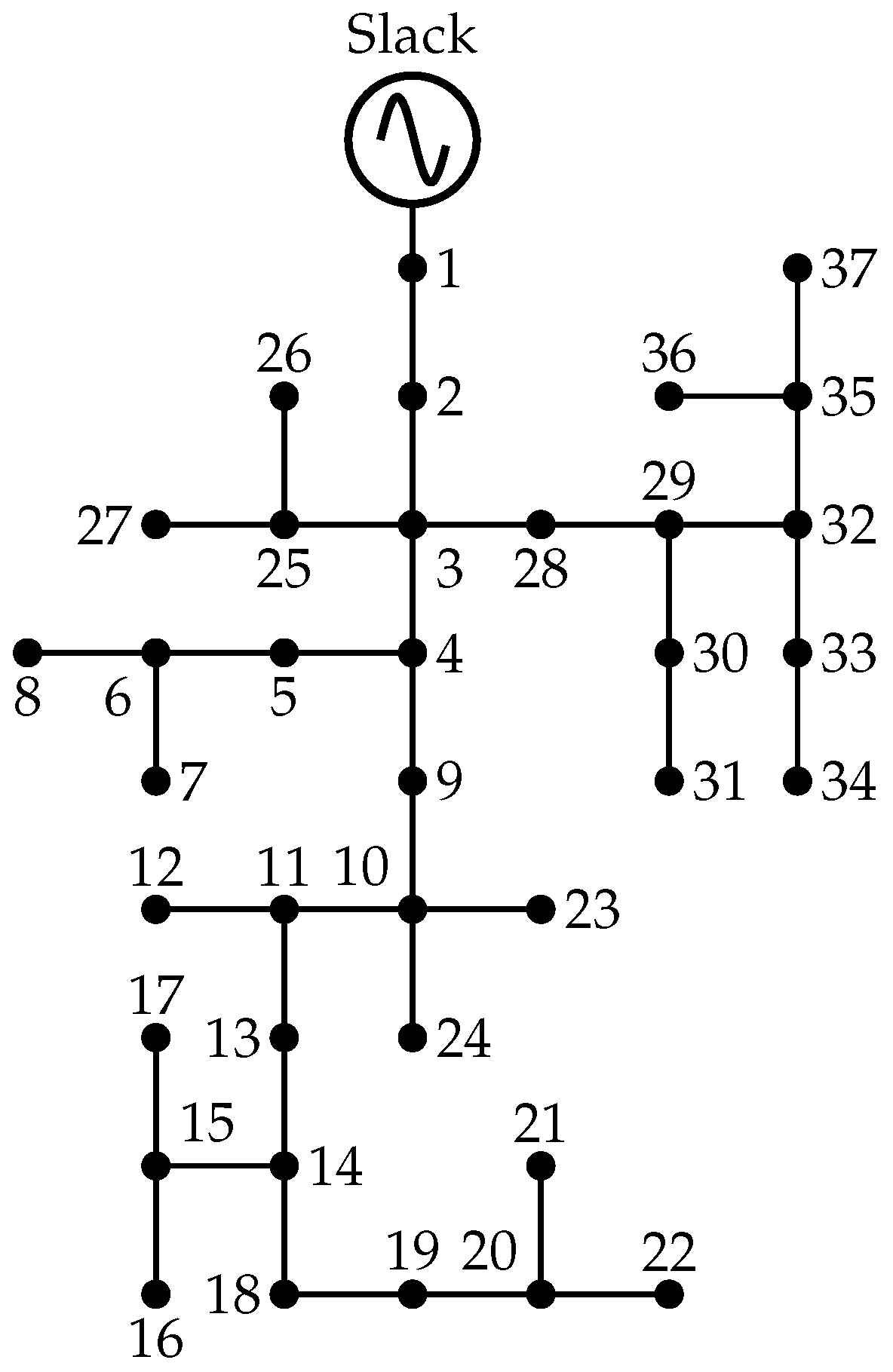
This section details the validation of the proposed methodology, which was carried out in two stages. First, our method was implemented on widely recognized test systems selected from the specialized literature (i.e., the 8-, 25-, and 37-node systems). These systems have been previously validated and used by other authors in similar problems involving unbalanced three-phase grids, and they exhibit the inherent characteristics of distribution systems: unbalanced loads, a radial topology, and line asymmetries. Thus, they adequately represent real network conditions. Subsequently, a comparative numerical analysis of the proposed mathematical models against previous studies was conducted. This analysis allowed verifying the consistency and accuracy of both the mathematical model and the proposed methodology.

6.1. Test Feeder Characteristics

The eight-node test system used in this work is characterized by a line-to-line voltage of 11 kV and a total installed power of 1005 kW and 485 kvar for phase A, 785 kW and 381 kvar for phase B, and 1696 kW and 821 kvar for phase C. The power losses of this system amount to 13.9925 kW. The single-line diagram of this feeder is shown in Figure 2 [36].

On the other hand, the 25-node test feeder operates with a line-to-line voltage of 4.16 kV. This system exhibits a power consumption of 1073 kW and 792 kvar for phase A, 1083.3 kW and 801 kvar for phase B, and 1083.3 kW and 800 kvar for phase C. Initially, the power losses of this system amount to 75.4207 kW. The electrical diagram of the 25-node system is presented in Figure 3 [36].

Finally, the 37-node system operates at a nominal voltage of 4.8 kV. Its total power consumption is 727 kW and 357 kvar for phase A, 639 kW and 314 kvar for phase B, and 1091 kW and 530 kvar for phase C. This system exhibits losses of 76.1357 kW. Its single-line diagram is shown in Figure 4 [36].

Further information related to the impedance matrices and three-phase power demand of each node can be found in [36].

These test systems were taken from the specialized literature to ensure a thorough validation of the proposed methodology. They represent realistic three-phase unbalanced distribution networks, where load asymmetries naturally arise due to the presence of single-, two-, and three-phase loads.

In real distribution networks, phase power imbalances occur because residential, commercial, and small industrial consumers often have single- or two-phase connections, leading to different power demands in each phase. This characteristic justifies the selection of the test systems as benchmarks to evaluate the effectiveness of the proposed MINLP models in optimizing phase-balancing strategies.

6.2. Computational Validation and Comparative Analysis

The proposed matrix (M-MINLP) and vector (V-MINLP) formulations for phase balancing were rigorously validated using the Julia programming software v1.10.2, leveraging the JuMP v1.21.1 optimization package and AmplNLWriter v1.2.1. All simulations were executed on a workstation equipped with a 12th Gen Intel Core i7-12700T CPU @ 1.40 GHz and 32 GB RAM, running on 64-bit Windows 11 Pro. Additionally, the formulations were compared against multiple literature-reported combinatorial optimization techniques based on metaheuristics, including the CBGA [36], the discrete VSA (DVSA) [36], the CSA [37], the improved CSA (ICSA) [37], the BHO [39], the sine–cosine algorithm (SCA) [39], the HOA [38], and the SSA [41]. Additionally, the proposed models were compared against convex approximations of the mathematical model, such as the mixed-integer quadratic convex model based on average power (MIQC-AP) [30], the mixed-integer quadratic convex model based on average current (MIQC-AI) [30], and the mixed-integer quadratic convex model based on electrical momentum (MIQC-EM) [30].

A detailed analysis of the results is presented below.

Table 2. Power losses for the 8-node system, as obtained with the methodologies reported in the literature and the proposed formulations.

Approach	Power Losses (kW)	Reductions (%)
Benchmark case	13.9925	–
MIQC-AP [30]	10.7613	23.0924
BHO [39]	10.5869	24.3388
CSA [37]	10.5869	24.3388
SCA [39]	10.5869	24.3388
CBGA [36]	10.5869	24.3388
DVSA [36]	10.5869	24.3388
ICSA [37]	10.5869	24.3388
HOA [38]	10.5869	24.3388
SSA [41]	10.5869	24.3388
MIQC-AI [30]	10.5869	24.3388
MIQC-EM [30]	10.5869	24.3388
M-MINLP	10.5869	24.3388
V-MINLP	10.5869	24.3388

presents the results reported in the specialized literature for the metaheuristic and exact solution techniques, along with the results obtained by our two proposed formulations, in the eight-node test system. The table organizes the information according to the implemented methodology, the reported power losses, and the percent reduction compared to the base case. It is important to note that, for this case, the power losses of the base case are 13.9925 kW.

In the eight-node test system, except for the MIQC-AP approach, all methodologies achieved identical results, with power losses of 10.5869 kW and a percent reduction of 24.34%. This uniformity is due to the relatively small solution space ($6^7$ = 279,936 combinations), which allows all methods to converge to the global optimum. These results validate the reliability and accuracy of the M-MINLP and V-MINLP formulations in small-scale systems.

The uniformity in the results for the eight-node test system indicates that the solution space is small enough for all optimization techniques (including metaheuristic methods and convex approximations of the mathematical model) to efficiently explore it in the search for the global optimum. This highlights the ability of the reported techniques to perform effectively when the problem size is manageable, and it validates the precision and robustness of the M-MINLP and V-MINLP formulations. From a practical standpoint, the results reinforce the reliability of exact formulations in ensuring optimal solutions, even in small systems. Furthermore, this test serves as a benchmark for validating the implementation and correctness of the optimization framework before scaling to more complex and computationally intensive scenarios. The ability of the proposed formulations to maintain precision under these conditions further demonstrates their suitability for both small-scale systems and larger, real-world distribution networks.

Table 3. Power losses for the 25-node system, as obtained by the methodologies reported in the literature and the proposed formulations.

Approach	Power Losses (kW)	Reductions (%)
Benchmark case	75.4207	–
MIQC-AP [30]	72.4061	3.9970
BHO [39]	72.3735	4.0403
CSA [37]	72.3296	4.0985
SCA [39]	72.3047	4.1315
MIQC-EM [30]	72.3017	4.1355
CBGA [36]	72.2919	4.1485
DVSA [36]	72.2888	4.1526
ICSA [37]	72.2888	4.1526
HOA [38]	72.2865	4.1556
SSA [41]	72.2865	4.1556
MIQC-AI [30]	72.2816	4.1621
M-MINLP	72.2801	4.1641
V-MINLP	72.2801	4.1641

presents the numerical results obtained for the 25-node test system, analyzing the same information as in Table 2.

Unlike the 8-node test system, the results for the 25-node feeder exhibit variations in power loss values and reduction percentages across optimization techniques. While all methods achieve a power loss reduction greater than 3.99%, the proposed formulations (M-MINLP and V-MINLP) stand out by achieving the lowest value, i.e., 72.2801 kW, corresponding to a 4.1641% reduction. This improvement highlights the robustness and precision of the proposed methodologies in handling medium-scale systems, where the solution space is exponentially larger ($4.7384\times {10}^{18}$ combinations) compared to smaller systems. In particular, the exact formulations outperform both the convex approximations and the metaheuristic approaches, which tend to be more prone to suboptimal solutions related to local optima.

It is worth noting that convex approximations such as MIQC-AI achieve results close to the proposed formulations but fall slightly short in terms of power loss minimization. Similarly, the best-performing metaheuristic techniques, i.e., HOA and SSA, achieve reductions of 4.1556%, demonstrating their effectiveness but still falling behind the precision of the exact formulations. From a practical perspective, our proposed methodologies offer two key advantages. Firstly, unlike metaheuristic methods, which rely on iterative heuristics and probabilistic search mechanisms, the exact formulations ensure convergence to the global optimum. Secondly, the methodologies are designed to handle the increased complexity of larger systems without compromising precision, as demonstrated in this test case.

These results reaffirm the relevance of the proposed formulations in medium-sized grids, where achieving precise and globally optimal solutions is critical for minimizing power losses and enhancing system efficiency. Furthermore, the performance gap between the proposed formulations and other approaches becomes increasingly significant as system complexity grows, emphasizing the suitability of the former for practical deployment in real-world scenarios.

Finally, the numerical results for the 37-node test system are presented in

Table 4. Power losses for the 37-node system, as obtained by the methodologies reported in the literature and the proposed formulations.

Approach	Power Losses (kW)	Reductions (%)
Benchmark case	76.1357	–
CSA [37]	61.6565	19.0176
CBGA [36]	61.5785	19.1201
DVSA [36]	61.4801	19.2493
HOA [38]	61.4797	19.2499
ICSA [37]	61.4781	19.2520
SSA [41]	61.4781	19.2520
M-MINLP	61.4748	19.2563
V-MINLP	61.4748	19.2563

. The same information as in the previous two test systems is analyzed. Note that, in this case, there are no results for the convex approximations of the mathematical model.

According to the results, all optimization methodologies significantly reduce power losses with respect to the benchmark case, achieving reductions above 19%. However, the M-MINLP and V-MINLP formulations report the lowest power losses (61.4748 kW for a 19.2563% reduction), highlighting their scalability and robustness, especially in systems with exponentially larger solution spaces ($1.7191\times {10}^{27}$ configurations for the 37-node system). While some metaheuristic techniques (e.g., SSA, ICSA) achieve reductions close to those of our proposal, they rely on stochastic iterative processes, increasing the likelihood of convergence to local optima in complex search spaces.

These results underscore the fundamental trade-off between solution quality and computational guarantees in phase-balancing optimization. Metaheuristic and convex approximation methods can obtain near-optimal solutions, but they lack global optimality guarantees, particularly in large-scale networks where the solution space is exponentially larger ($4.7384\times {10}^{18}$ for the 25-node system and $1.7191\times {10}^{27}$ for the 37-node system). In such cases, metaheuristic approaches often fail to fully explore the solution space, leading to suboptimal solutions due to premature convergence or inadequate search strategies.

In contrast, our M-MINLP and V-MINLP formulations leverage exact mathematical programming, ensuring a systematic and exhaustive exploration of all feasible configurations. The combination of interior-point methods with branch-and-cut techniques allows these models to achieve mathematically rigorous and globally optimal solutions, eliminating the uncertainty associated with metaheuristic approaches. While the observed improvements regarding power losses over previous methodologies may appear small (<0.004%), their significance lies in the guarantee of optimality rather than in the absolute gain. This is particularly relevant in the electrical planning of distribution systems, where even small enhancements in efficiency may lead to significant long-term economic and operational benefits.

The practical relevance of these results lies in their scalability to real-world distribution networks. The minimal performance differences between the proposed formulations and the best-performing metaheuristics emphasize the importance of using exact methods in problems of this scale, where precision is critical. Additionally, the results highlight the limitations of metaheuristic approaches in reliably achieving optimal solutions as system complexity increases. This confirms that exact optimization techniques are more suitable for medium-scale distribution networks, where power loss minimization directly impacts operational efficiency and cost-effectiveness.

Moreover, the convergence of all methodologies in the eight-node case validates the robustness of the proposed models. Since the eight-node system has a relatively small search space (279,936 possible phase allocations), all methodologies, including the metaheuristic ones, can effectively explore the feasible solutions and reach the same result. However, as the system size increases, the computational challenges associated with combinatorial complexity become more pronounced, reinforcing the need for exact optimization approaches that ensure global optimality.

Regarding computational performance, M-MINLP consistently outperforms V-MINLP in terms of solution time, being 15.6 times faster for the 8-node system, 4.4 times faster for the 25-node system, and 2.5 times faster for the 37-node system. This difference in efficiency becomes increasingly relevant as the system grows larger. However, given the vast solution space, the computational times remain remarkably short – note that, if one combination were evaluated every 10 ms, it would take over 150 million years to explore all configurations in the 25-node system, as well as billions of years for the 37-node system. These results highlight the efficiency of our approach, demonstrating that global optima can be obtained within practical time frames.

These findings reaffirm the necessity of methodological precision in addressing combinatorial optimization problems involving power systems. The proposed M-MINLP and V-MINLP formulations provide a reliable, scalable, and computationally efficient approach to phase-balancing optimization, laying a solid foundation for future advancement in power distribution network planning and operation.

6.3. Complementary Analysis

To further illustrate the impact of the proposed phase-balancing optimization, this section presents a detailed comparative analysis of system imbalance and voltage profile before and after implementing the optimization strategy. While the primary objective of the methodology is to minimize power losses, the results also demonstrate its effectiveness in reducing system unbalance, which directly influences voltage asymmetry.

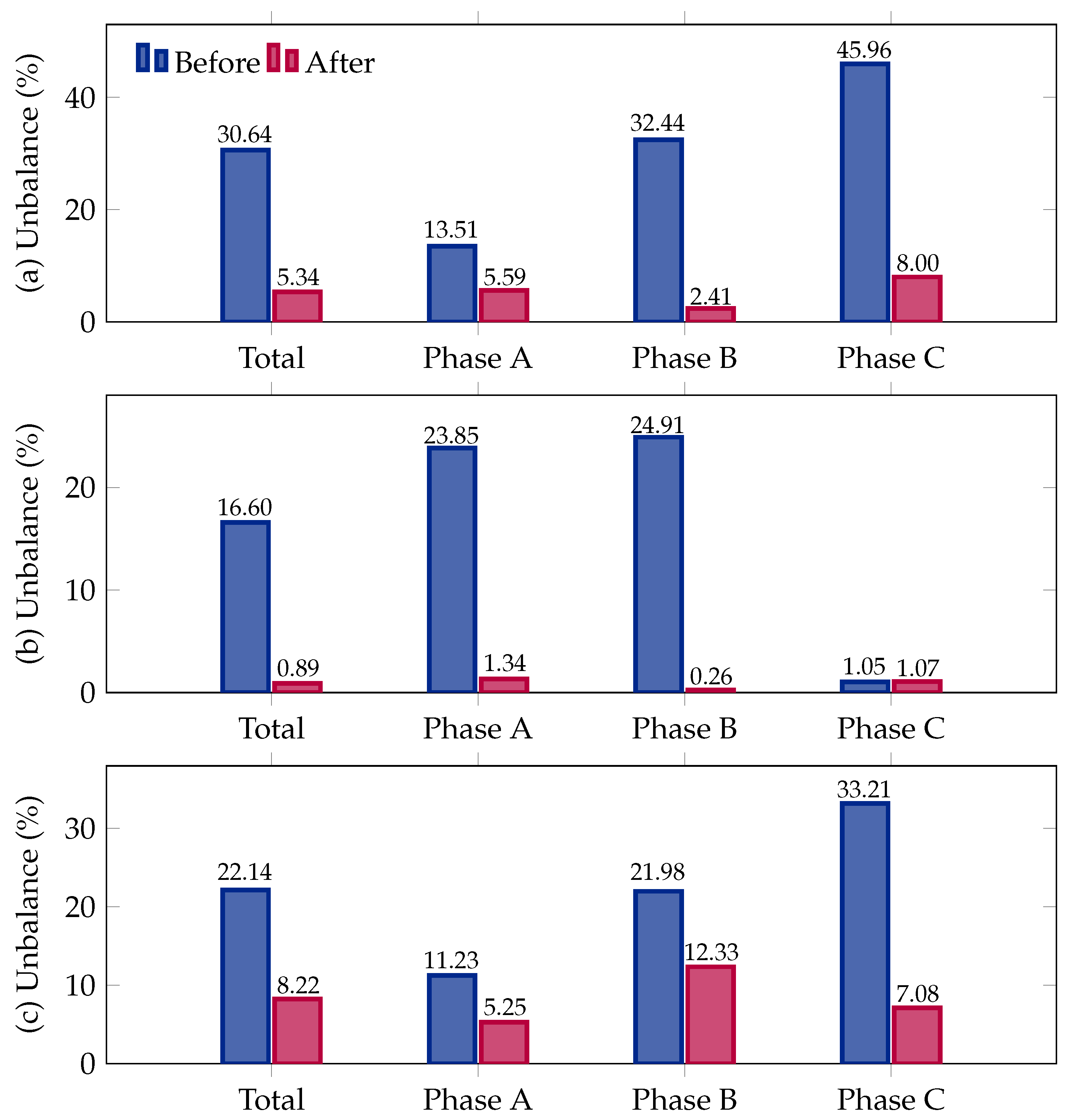
Figure 5 illustrates the percentage of current unbalance before and after applying the proposed phase-balancing methodology across three different test systems: 8-node, 25-node, and 37-node feeders.

The results demonstrate a significant reduction in unbalance, reinforcing the effectiveness of the optimization approach.

• The implementation of the proposed methodology results in a significant reduction ub total unbalance in the eight-node system, decreasing from 30.64% to 5.34%, an 82.57% improvement. The phase-specific corrections show notable reductions, particularly in Phase B, where unbalance drops from 32.44% to 2.41%, and in Phase C, where it decreases from 45.96% to 8.00%.
• For the 25-node system, the proposed phase-balancing methodology achieves the highest percentage reduction in unbalance, improving from 16.60% to 0.89%, a 94.6% reduction. The largest improvement is observed in Phase B, where unbalance drops from 24.91% to 0.26%, followed by Phase A, which decreases from 23.85% to 1.34%. Phase C remains largely unchanged, indicating that this phase was already well balanced before optimization.
• In the 37-node system, the total unbalance is reduced from 22.14% to 8.22%, representing a 62.9% improvement. Phase C exhibits the largest absolute reduction, decreasing from 33.21% to 7.08%, followed by Phase A with a drop from 11.23% to 5.25%. Phase B sees a moderate improvement, decreasing from 21.98% to 12.33%. While some residual unbalance remains, particularly in Phase B, the methodology effectively minimizes phase disparities and improves overall system performance.

The proposed optimization methodology successfully reduces system unbalance, leading to better phase balancing, improved current distribution, and enhanced network unbalance. The results validate the effectiveness of the approach in both small and large networks, demonstrating its practical applicability for real-world distribution systems.

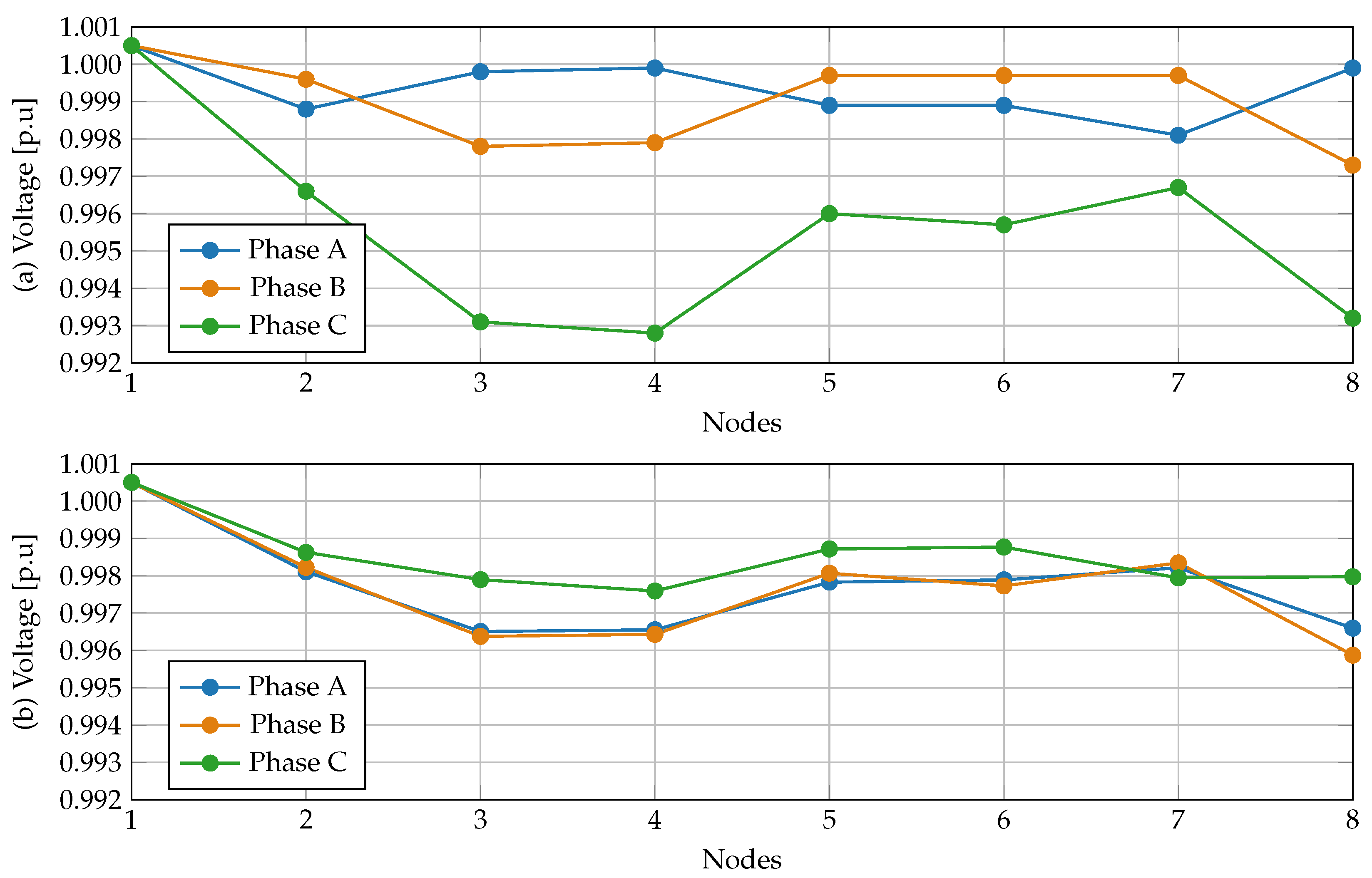
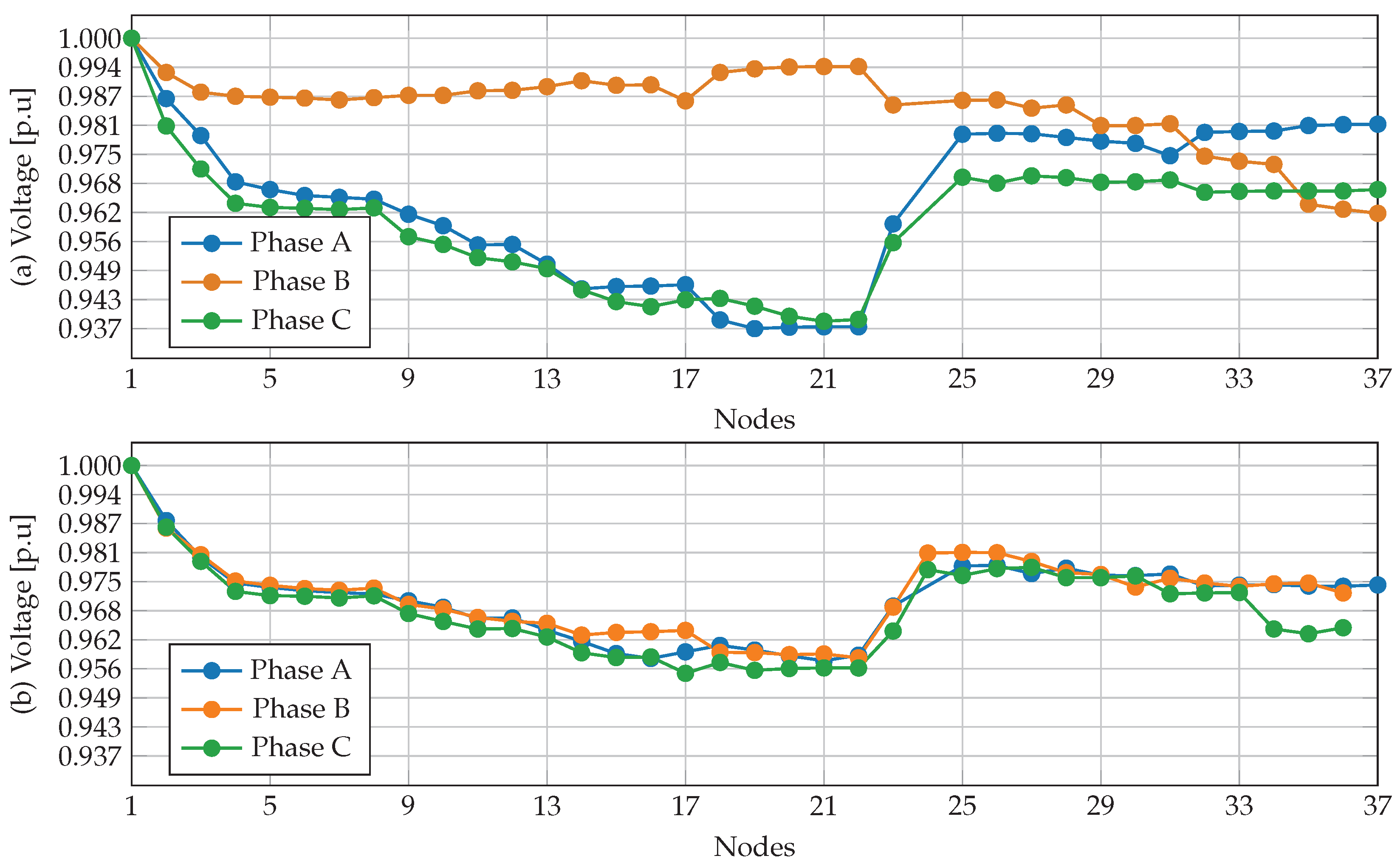
Figure 6, Figure 7 and Figure 8 illustrate the voltage profiles for the 8-node, 25-node, and 37-node systems, respectively, before and after implementing the proposed phase-balancing methodology. The results show a notable improvement in voltage uniformity, demonstrating that optimizing phase connections not only reduces power losses but also enhances voltage unbalance across the network.

Figure 6 illustrate that the voltage profile before optimization reveals significant phase disparities, particularly at nodes 3, 5, and 8, where Phase C experiences the most pronounced voltage drop. After phase balancing, the voltage levels across phases become more uniform, reducing phase separation and improving overall voltage symmetry.

Regarding to 25-node test system (Figure 7), initially, the voltage profile exhibits clear phase separation, especially in the mid-section of the network (nodes 7–20), where Phase A and Phase C show the largest deviations. After applying the phase-balancing optimization, voltage unbalance is significantly reduced, with phase voltages aligning towards a more balanced distribution. This improvement suggests that the methodology successfully redistributes loads, leading to a more stable network with lower phase-to-phase deviations.

Finally, in the 37-node test system, before phase balancing, the voltage profile is highly unbalanced, particularly in the lower voltage regions (nodes 7–30), where Phases A and C experience a notable drop. After optimization, voltage levels become more consistent, with a substantial reduction in phase differences, particularly in critical nodes. The improvements are most evident in the mid-to-late sections (nodes 25–37), where phase voltages align more closely, validating the method’s effectiveness in larger, more complex distribution networks.

The results across all three test systems demonstrate that the proposed phase-balancing optimization methodology effectively reduces both power losses and voltage unbalance. The most pronounced improvements are observed in larger networks, where initial phase disparities were more severe. By minimizing the distribution lines’ current, related to power losses, the methodology naturally mitigates current unbalance, which is the primary driver of voltage unbalance in distribution networks. Since voltage drops are directly proportional to current flow, reducing excessive unbalanced currents prevents disproportionate voltage deviations across phases, leading to a more stable and uniform voltage profile. This confirms that optimizing phase assignments not only enhances network efficiency by reducing power losses but also improves power quality by mitigating voltage imbalance, reinforcing the practical applicability of the proposed approach in real-world distribution networks.

6.4. Computational Complexity Analysis

This subsection analyzes the computational complexity of the proposed M-MINLP and V-MINLP formulations, evaluating their scalability and performance in solving the optimal phase-balancing problem. The computational complexity of these models is influenced by several factors, including the number of binary decision variables and constraints.

Table 5. Model characterization regarding the number of variables.

Variable Name	Variable	M-MINLP Variables	V-MINLP Variables	Type
Objective function	$p_{loss}$	1	1	Real
Voltage drop	${\mathbb{V}}_{j3\phi }$	$3l$	$3l$	Complex
Current flow	${\mathbb{I}}_{j3\phi }$	$3l$	$3l$	Complex
Current injection	${\mathbb{I}}_{k3\phi }^g$	$3n$	$3n$	Complex
Current consumption	${\mathbb{I}}_{k3\phi }^d$	$3n$	$3n$	Complex
Wye current consumption	${\mathbb{I}}_{k3\phi }^Y$	$3n$	$3n$	Complex
Triangle current consumption	${\mathbb{I}}_{k3\phi }^{\Delta }$	$3n$	$3n$	Complex
Voltage	${\mathbb{V}}_{k3\phi }$	$3n$	$3n$	Complex
Final load connection	${\mathbb{S}}_{kf3\phi }^1$	$3n$	$3n$	Complex
Matrix load phase connection	$x_{kfg}$	$9n$	–	Binary
Vector load phase connection	$x_{kc}$	–	$6n$	Binary
Total variables		$1+15n+6l$	$1+12n+6l$

and

Table 6. Model characterization regarding the number of equations, inequalities, and objective functions.

Equation Name	Equation	M-MINLP Constraints	V-MINLP Constraints	Type
Objective function	(1)	1	1	Real
Power flow	(2)	n	n	Complex
Line voltage drop	(3)	$2l$	$2l$	Complex
Load current	(4)–(6)	$3n$	$3n$	Complex
Voltage regulation	(8)	n	n	Complex
Final load connection	(9) and (12)	n	n	Complex
Matrix phase load connection	(10) and (11)	$2n$	–	Binary
Vector phase load connection	(13)	–	n	Binary
Total equations and inequalities		$1+7n+2l$	$1+6n+2l$

characterize the mathematical model according to these factors.

Table 5 and Table 6 provide a detailed characterization of the variables and constraints of the M-MINLP and V-MINLP models, allowing for an analysis of their computational complexity. In terms of variables, the M-MINLP model introduces more binary constraints ($9n$) by using a matrix representation for phase configuration, whereas the V-MINLP model employs a vector representation with fewer binary constraints ($6n$) but with a larger number of possible combinations in the optimization process.

In the M-MINLP formulation, the connection for each node is not modeled using a simple binary variable to indicate whether a load is connected to a specific phase; instead, it is represented through a rotation matrix (Table 1). Each node has three binary variables per phase, corresponding to each position within the matrix, and additional constraints, i.e., Equations (10) and (11), are imposed to ensure that only one of the six possible matrices is selected. This approach accurately models the cyclic rotation of phases, which is essential for optimizing the load balance. By fixing a reference phase at each node, the valid options are reduced to only two in order to satisfy Constraints (10) and (11). For example, if the model fixed the first position to phase A at node 2, the only valid options would automatically be $R_1$ (ABC) or $R_4$ (ACB). Thus, the model scales with a complexity of $O\left(2^N\right)$.

In contrast, in the V-MINLP formulation, each node utilizes a vector of six binary positions, where only one can take the value of 1 i.e., Equation (13). This means that each node has six independent phase connection possibilities, resulting in an exponential growth of $O\left(6^N\right)$. This greater flexibility translates into a more aggressive exponential growth compared to M-MINLP, making this approach less computationally efficient for medium-sized and large networks. Therefore, M-MINLP is a more suitable option for larger-scale networks, as its more restrictive structure allows for a more efficient exploration of the solution space. Meanwhile, V-MINLP may be preferable for small networks, where the flexibility in phase allocation does not impose a prohibitive computational burden.

In this regard, the main difference between the proposed formulations lies in the mathematical representation of the load connection model. To facilitate the understanding of the results presented herein, the following comparison table is included:

Table 7. Comparison of M-MINLP and V-MINLP formulations.

Feature	M-MINLP	V-MINLP
Number of variables	$1+15n+6l$	$1+12n+6l$
Number of constraints	$1+7n+2l$	$1+6n+2l$
Computational complexity	$O\left(2^N\right)$	$O\left(6^N\right)$
Computation time	Faster for large-scale systems	Slower due to computational complexity
Optimality guarantee	Ensures global optimality	Ensures global optimality
Best use case	More efficient for large networks	Suitable for small to medium-sized networks

compares the M-MINLP and V-MINLP formulations in terms of their number of variables, constraints, computational complexity, and efficiency. Note that M-MINLP introduces a slightly higher number of variables ($1+15n+6l$ vs. $1+12n+6l$) and has more constraints ($1+7n+2l$ vs. 1$+6n+2l$). In terms of complexity, M-MINLP scales with $O\left(2^N\right)$, which is significantly better than the $O\left(6^N\right)$ scaling of V-MINLP. This explains its high efficiency in large-scale networks. Although both models ensure global optimality, V-MINLP incurs a higher computational cost, making it more suitable for small or medium-sized networks. In this sense, M-MINLP is a more efficient option for large distribution systems, whereas V-MINLP offers greater flexibility in phase allocation, albeit at the expense of a higher computational burden.

6.5. Limitations and Biases of the Proposed Methodology

Though robust and effective, the proposed methodology for optimal phase balancing in unbalanced three-phase distribution networks has some inherent limitations and biases:

• As the system size increases, the solution space grows exponentially. This is evident in the 25- and 37-node test systems, where the number of possible combinations reaches values of $4.7384\times {10}^{18}$ and $1.7191\times {10}^{27}$, respectively. This growth significantly impacts the solution time, especially for V-MINLP, which is slower compared to M-MINLP. Although the solution times are relatively short in comparison with the exhaustive evaluation of all possible combinations, for larger-scale systems, it may be necessary to implement complexity reduction strategies or parallelization.
• Our methodology relies on the use of advanced solvers such as BONMIN. While these tools are effective in ensuring optimal solutions, their performance may be limited by hardware configurations or restrictions related to memory and processing capacity, especially as the number of system nodes increases.
• The test systems used were designed to represent the typical characteristics of distribution networks but do not account for uncertainties, such as variations in load consumption.
• The results show that the M-MINLP and V-MINLP formulations are capable of achieving optimal solutions, even in large solution spaces, while metaheuristic-based techniques may become trapped in local optima. However, the use of metaheuristics could be more efficient in terms of execution time if near-optimal solutions are prioritized over exact ones.

These limitations underscore the need for future research to improve the scalability and robustness of the method, including the exploration of hybrid approaches that combine the accuracy of MINLP models with the efficiency of metaheuristic techniques. Additionally, it would be useful to validate the methodology in larger-scale systems and with data representative of real operating conditions.

7. Conclusions

The proposed MINLP formulations for optimal phase balancing in three-phase distribution networks demonstrate robust performance and scalability, particularly when addressing the inherent computational complexity of the problem. Both models (M-MINLP with its matrix-based representation and V-MINLP with its vector-based approach) operate within an exponential solution space of $6^{n-1}$. Our numerical results show that the M-MINLP formulation significantly outperforms the V-MINLP model in terms of computational efficiency. For example, the M-MINLP model solved the 8-node, 25-node, and 37-node systems in 8.14 s, 2428.33 s, and 31,891.48 s, respectively, achieving speed improvements of up to 15.6 times over the V-MINLP model.

Moreover, when compared against eight metaheuristic optimizers and three convex approximations, the proposed formulations not only delivered substantial improvements in power loss reduction (with final losses of 10.5869 kW, 72.2801 kW, and 61.4748 kW for the 8-, 25-, and 37-node feeders, respectively); they also exhibited superior computational performance. While the V-MINLP model offers greater flexibility in phase balancing, its computational cost escalates more aggressively, making it less suitable for medium-sized and large networks. Conversely, the more restrictive structure of the M-MINLP model allows for more efficient exploration of the solution space, ensuring globally optimal solutions within a reasonable time frame, even for larger systems.

By combining an interior-point method with a branch-and-cut approach in Julia, our formulations could effectively manage the combinatorial explosion typical of distribution network expansion problems while also ensuring global optimality. These computational advantages, together with significant enhancements in power loss reduction, confirm the practical viability of the proposed models for advanced electrical distribution network planning.

Future research could focus on extending the proposed MINLP formulations to address optimal conductor selection in three-phase asymmetric networks while integrating technical and economic factors. In addition, some promising directions include minimizing the expected power losses in bipolar DC networks with unbalanced monopolar loads and incorporating renewable energy sources to enhance system balance and reduce losses. Incorporating uncertainties in load demand, renewable generation, and dynamic operating conditions would further increase the robustness and applicability of the methodologies, making them better suited for the challenges of real-world distribution networks. Finally, phase balancing could be optimized alongside the integration of DGs, capacitor banks, or reactive compensation devices to enhance the efficiency of three-phase distribution systems. These advancements would strengthen the methodology’s impact on power systems optimization.