Single-Level and Two-Level Circuit Solutions for Buck-Boost AC Voltage Regulators with Phase-by-Phase Switches

Abstract

Forming required AC voltage levels is currently one of the most pressing problems. Unstable voltage levels can lead to the failure of household and industrial equipment. This can lead to a pure effect on the production cycle. In this regard, the development of AC voltage regulators has become relevant. Such regulators can perform the function of voltage level asymmetry compensators in a three-phase power supply network. In turn, new topologies should be energy-efficient and reliable. This can be achieved by reducing the number of semiconductor elements, thus reducing losses and increasing efficiency. Also, AC voltage regulators have found applications as soft-start devices for motors and have become relevant to frequency converters. The power level of such devices can vary from units to tens of kilowatts. This paper presents several circuit design solutions for AC voltage regulators with fewer switches. These solutions are made according to both a single-level and two-level system, where the level refers to the number of links that increase the transmission coefficient. The schemes were analyzed, and efficiency was evaluated through their harmonic coefficients, power factor, and efficiency coefficient. For the basic scheme, a photo of the experimental layout and its results are provided.

1. Introduction

Currently, there are many regulators in the field of power electronics, both DC/DC and AC/AC, which this article will be devoted to. AC/AC converters can include both combinations of two types of AC/DC and DC/AC, as well as a separate class of converters—cycloconverters or matrix converters, which primarily allow you to obtain a frequency–controlled voltage at the output. Nevertheless, the main class of AC voltage regulators fulfills the main purpose of regulating the output voltage. It is worth mentioning here the application scope of such devices; these are motor soft-starters, voltage stabilizers, and devices for improving the quality of electrical energy, which can be regulated by state standards for quality indicators GOST 32145-2013 in the Russian Federation and the USA IEEE 1159.3.

Soft-start devices for motors were required when direct start became ineffective and often had a destructive character. Among the methods of motor starting, constructive ones can be distinguished and used by an additional device. Thus, motors with a short-circuited rotor can start directly, which can disable it due to high starting currents and smoothness. Rheostats can serve as an additional device for which the resistance may change depending on the position of the slider. After rheostatic start-up, a soft-start device can be used. Both frequency or speed converters and voltage regulators can be included here. The motor speed is changed according to user-configurable characteristics, which also affects the acceleration time of the motor [1,2,3,4]. Switching between the connections of the star-triangle windings can also perform a smooth start of the motor, this circumstance reduces the starting currents three times.

The most popular method of motor starting is performed through a frequency converter. It can be either a direct frequency converter, a matrix converter, or a two-link combination of a rectifier and an inverter. The output frequency is controlled by the user through the control system. Another soft-start method is considered to be voltage regulation while maintaining frequency. The classical circuits of a thyristor AC voltage regulator are built according to the scheme of counter-parallel switching of thyristors. As the output voltage of the regulator increases, the torque gradually increases, and the motor starts accelerating. The main advantage of such devices is the ability to accurately adjust the torque. Semiconductor converters have one advantage over mechanical devices—a soft stop of the motor. The main types of loads requiring a smooth start are pumps, conveyors, fans, and compressors. The recommended motor start time can be up to 10 s, and the stop time from 0 to 20 s, depending on the power and type of motor. Such soft-start devices can be used for parallel and sequential start-up of several motors.

The main disadvantage of such devices can be considered the presence of odd harmonics in the output signal, which significantly worsens the values of the harmonic coefficient and affects the increased consumption of reactive power at the input [5,6]. This can be corrected through the introduction of a new algorithm [7,8]. It is enough to monitor the voltage to achieve the required motor speed since voltage and speed are proportionally related [9]. From the point of view of the theory of automatic control, systems with a proportional integral regulator, a neural network, and an observer can be used, all of which can increase the efficiency of the system and reduce starting currents by increasing the acceleration time [10].

Nevertheless, such regulation spoils the supply network by adding a reactive component at the input. This is caused by the distortion of the inrush currents due to phase control [11]. This effect is observed in single-zone or single-level thyristor AC voltage regulators. By introducing several levels into the structure of the regulator, the quality of inrush currents can be improved. One of the solutions to this problem is the use of a multi–winding transformer or an analog in the form of a capacitor voltage divider. A smooth voltage change is carried out by the transformation coefficient changing by switching between the transformer windings or adding voltage levels with additional divider capacitors [12,13,14,15,16].

The main manufacturers of soft-start devices include the following global manufacturers: ABB, Ansaldo, Emotron AB, Schneieder Electric, Siemens, Sirius, Softtronic, and Telemecanique. The power of such devices varies from units to hundreds of kilowatts. AC voltage regulators can be connected to either one or several phases of the motor. In the case of a single phase, the device mitigates the increase in the starting torque than the current. Two-phase soft-start devices are most often used. For cases of more powerful systems, three-phase ones are used. The disadvantages of phase-by-phase control are nonlinear and phase-asymmetric current consumption, which can be compensated by control algorithms but still negatively affects the network and the motor [17,18].

In this regard, it follows that the problem of creating an effective soft-start device is relevant. In such a soft starter device, it is possible to improve the shape of voltage and current, as well as reduce the number of semiconductor elements, which can increase the reliability of the system and reduce its dimensions.

AC voltage regulators can also be used as voltage stabilizers or network asymmetry compensators. An alternating current stabilizer is a converting device, the main purpose of which is to protect electrical appliances from the effects of fluctuations and voltage surges in the supply network, which can lead them to breakage and failure. In many modern automatic voltage regulators (AVR—Automatic Voltage Regulator), an autotransformer is still used as a conversion device. The most advanced inverter devices of the new generation use the technology of double, transformer-free conversion of electrical energy.

Depending on the type of supply voltage for which the stabilizers are designed, there are single-phase, three-phase, and 3:1 (“three-in-one”) devices. The former are used only to stabilize the power supply of single-phase electrical appliances. Three-phase stabilizers are designed to operate in three-phase networks to power equipment designed for 380 V, but with phase-by-phase load distribution, they can also be used to power single-phase electrical appliances [19].

Many modern AC voltage stabilizers also have a number of additional functions:

(1)

Correction of the output voltage waveform;

(2)

Protection against overheating and short circuits in the load supply circuit;

(3)

Protective shutdown of the device at unacceptable input voltage values (the required threshold along the upper and lower boundaries can be set by the user independently);

(4)

Suppression of RF and pulse interference by the output filter;

(5)

The ability to set the required output voltage values different than the standard ones;

(6)

The possibility of implementing parameter monitoring and remote control of the stabilizer.

Depending on the principle of operation, there are five types of stabilizers: ferroresonance (voltage conversion is based on the phenomenon of electromagnetic ferroresonance—magnetic saturation of ferromagnetic choke cores), electromechanical (their device has a servo drive that provides switching of current-removing brushes that remove secondary voltage from the coils of the autotransformer winding.), relay (according to the principle of voltage conversion, they can be attributed to analogs of servo-driven devices, the difference between them is in the method of transmitting secondary voltage from the autotransformer), electronic (switching of the output voltage is carried out by semiconductor power switches—thyristors or triacs, the main advantage of these more advanced devices is high performance), and inverters (the operation of an inverter stabilizer can be described as the conversion of an alternating voltage to a constant by a rectifier, followed by conversion to a stabilized alternating sinusoidal output variable).

The quality of electrical energy can be controlled by specialized meters, some of which may already show the level of harmonic current and voltage, power factor, as well as quality indicators; for example, it would be possible to deduce the level of asymmetry or at least confirm that the three-phase network is asymmetric and the necessary measures need to be taken to elimination. The cause of the asymmetry of the three-phase network voltage may be an asymmetrically distributed load. Also, due to the presence of a neutral wire, asymmetry can lead to overloads of the neutral current. You can compensate for the asymmetry in both passive and active ways. Passive ones include the use of capacitors with asymmetrically distributed capacitance values in phases [20], the Steinitz scheme, and a combination of ranges and chokes [21]. An alternative solution may be active filters that compensate for the zero sequence, reactive power, and higher harmonics in the current spectrum. Such devices have a fairly large number of switches, from 6 to both IGBT and MOSFET transistors. The asymmetry of the mains voltage affects the voltage fluctuation, both drawdown and overvoltage, which for the consumer results in failures of the devices, up to their failure. In asymmetric three-phase networks, there will be zero and reverse sequence currents. These currents lead to an increase in power losses, reducing efficiency and reliability. Networks where this effect can be observed: railway networks, networks with induction and arc furnaces with high-power furnaces. Symmetrical transformers may already be applicable here due to the high load capacities [22]. In addition to uneven load distribution, phase interruptions and short circuits are possible, which can also be equated to uneven load distribution in a three-phase network, but more critical. Here, static codes [23], circuit solutions using a volt-additive transformer [24], as well as proposed AC voltage regulators that allow equalized dips and voltage surges in a three-phase network can serve as compensators for asymmetry [25]. Thus, a buck-boost regulator with phase-by-phase switches was proposed. This converter allows you to increase or decrease the voltage in the range of 0–1.6 times relative to the nominal level.

Thus, the problem of effective AC voltage regulators developing with the function of improving the quality of electrical energy, including compensation for asymmetry due to the buck-boost conversion function, is urgent. In which, as in the soft-start device, the form of voltage and current will be improved, as well as the number of semi-conductor elements will be reduced, primarily compared with the inverter type of stabilizers. The proposed variant of the AC voltage regulator, compared with existing solutions, will have a larger range of output voltage regulation up to 1.6 times, compared to 1.3 for known solutions [26].

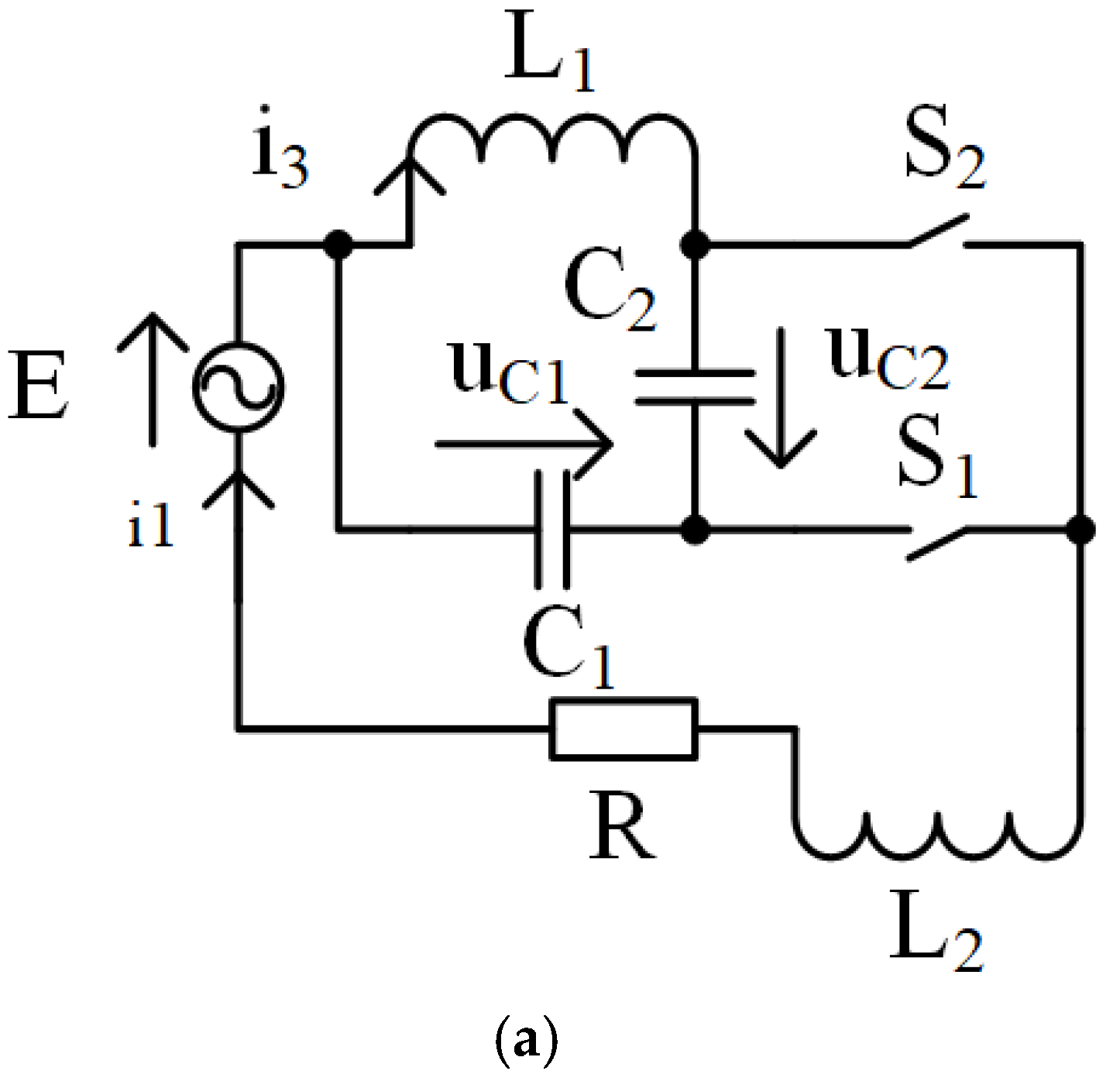
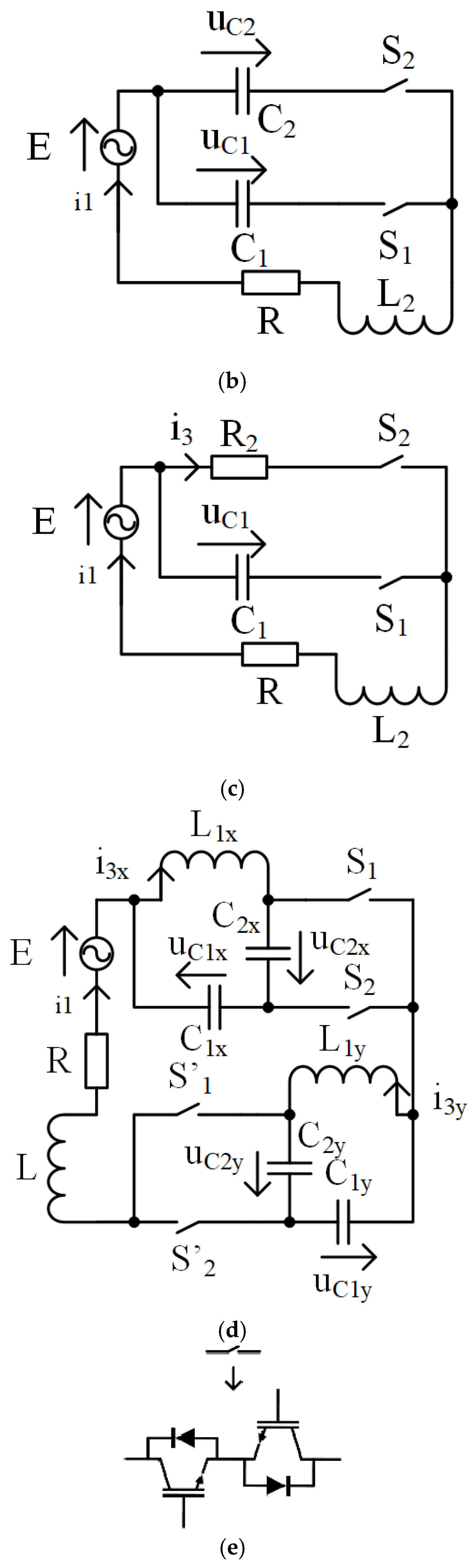
2. Circuit Design of AC Voltage Regulators with Phase-by-Phase Switches

A family of new energy-efficient buck-boost AC voltage regulators (RAV) with phase-by-phase switches is proposed in Figure 1.

The principle of the regulator operation, for the basic version: high-frequency pulses, alternately turn on the switches S₁ and S₂, switch-on and switch-off circuits containing either a capacitor C₁ or a reactor L₁. By switching between the vectors of the first harmonics of the voltages U₁ and U_L1, it is possible to obtain the necessary voltage U_out on the load. The resulting U_out vector is determined by the geometric sum of the vectors qU_C1 and (1-q)U_L1 and depends on the relative time q of their inclusion. Due to the C₂ capacitor, during the switch-off of the reactor branch, the accumulated energy is redirected to the capacitor branch.

This topology can be simplified by switching either the reactor or only the capacitor branch. For the corresponding circuit, a damping resistor and a capacitor are additionally installed, which are necessary to reset the energy stored in the reactor, or resistance must be connected in parallel to the switch, which allows damping the L₁C₁ circuit, thereby improving the quality of the voltage in the load.

Also, in turn, you can replace the reactor L₁ with a capacitor, remove the damping capacitor as well, or leave only one capacitor, as in Figure 1c. The resistor R₂ in this circuit acts as the resistance of switch S₂, which will be necessary for the mathematical calculation that will be presented below. There is no need for this additional resistor because it will only reduce the efficiency of the system. Also, here is a two-level version of the converter, as shown in Figure 1d; it is a cascade connection of two or more basic circuits of the regulator. Figure 1e shows a variant of the AC switch, in the role of which the GD200CEY120C2S module from STARPOWER will be used, which will also be presented later in the experiment section. Such converters do not have a transformer in their composition, which reduces their mass parameters. The proposed buck-boost RAV with phase-by-phase switches has almost sinusoidal input and output currents and the ability to increase the voltage conversion coefficient per unit.

3. Mathematical Model

Using the method of differential equations algebraization (DEA) [27], mathematical models of buck-boost RAV with phase switches were constructed. The principle of constructing such mathematical models is based on writing differential equations according to Kirchhoff’s laws and further algebraizing them, i.e., averaging over the period of each desired variable, as well as splitting variables into their active and reactive components in order to exclude the presence of phases in the equations. Such variables can include both currents and voltages. In Figure 1, The RAV schemes are presented, for which mathematical models were obtained and energy characteristics, regulatory and external, were obtained from them.

In order to take into account the operation of the transistors in the circuit, two versions of the systems of equations are written when the switch S₁ or S₂ is closed via a switching function (1):

$${\mathsf{\psi }}_1(t)=M+{\displaystyle \frac{\sin \left(2\pi M\right)}{\pi }}\cos \left(2\pi f_{h}t\right)+{\displaystyle \frac{1-\cos \left(2\pi M\right)}{\pi }}\sin \left(2\pi f_{h}t\right),$$

(1)

$${\mathsf{\psi }}_{\sin }={\displaystyle \frac{M}{2}}+{\displaystyle \frac{\sin \left(2\pi M\right)}{T\pi }}{\displaystyle \frac{8{\pi }^2\sin \left(T2\pi f_h\right)}{2\pi f_h\left(16{\pi }^2-T^{2}4{\pi }^2{f}_h^2\right)}}+{\displaystyle \frac{1-\cos \left(2\pi M\right)}{T\pi }}{\displaystyle \frac{16{\pi }^2\left[{\cos }^2\left(T\pi f_h\right)-1\right]}{T^{2}8{\pi }^3{f}_h^3-16{\pi }^{2}2\pi f_h}},$$

(2)

$${\mathsf{\psi }}_{\cos }={\displaystyle \frac{M}{2}}+{\displaystyle \frac{\sin \left(2\pi M\right)}{T\pi }}{\displaystyle \frac{\sin \left(T2\pi f_h\right)\left(8{\pi }^2-T^{2}4{\pi }^2{f}_h^2\right)}{2\pi f_h\left(16{\pi }^2-T^{2}4{\pi }^2{f}_h^2\right)}}+{\displaystyle \frac{1-\cos \left(2\pi M\right)}{T\pi }}{\displaystyle \frac{2{\sin }^2\left(T\pi f_h\right)\left(8{\pi }^2-T^{2}4{\pi }^2{f}_h^2\right)}{2\pi f_h\left(16{\pi }^2-T^{2}4{\pi }^2{f}_h^2\right)}},$$

(3)

where index 1 shows that the calculation is based on the first harmonic, M—is the modulation depth, f_h—is the key switching frequency, T—is a period of the grid, and sin (2) and cos (3) formulas indicate the active and reactive components, respectively.

For the basic LCC circuit, please see Figure 1a, (4), (5):

$$\begin{array}{l}{S}_1=1\\ \left\{\begin{array}{l}{U}_{C1}+U_{C2}-L_1\cdot {\displaystyle \frac{d{I}_3}{dt}}=0\\ L_1\cdot {\displaystyle \frac{d{I}_3}{dt}}-U_{C2}+R\cdot I_1+L_2\cdot {\displaystyle \frac{d{I}_1}{dt}}=E\\ I_1-C_1\cdot {\displaystyle \frac{d{U}_{C1}}{dt}}-I_3=0\\ U_{C1}+R\cdot I_1+L_2\cdot {\displaystyle \frac{d{I}_1}{dt}}=E\end{array}\right.\end{array},$$

(4)

$$\begin{array}{l}{S}_2=1\\ \left\{\begin{array}{l}{U}_{C1}+U_{C2}-L_1\cdot {\displaystyle \frac{d{I}_3}{dt}}=0\\ L_1\cdot {\displaystyle \frac{d{I}_3}{dt}}+R\cdot I_1+L_2\cdot {\displaystyle \frac{d{I}_1}{dt}}=E\\ I_1-C_1\cdot {\displaystyle \frac{d{U}_{C1}}{dt}}-I_3=0\\ U_{C1}+U_{C2}+R\cdot I_1+L_2\cdot {\displaystyle \frac{d{I}_1}{dt}}=E\end{array}\right.\end{array},$$

(5)

where S₁ = 1 indicates that switch S₁ is switched on and S₂ is switched off, and S₂ = 1 indicates that the switch S₂ is switched on and S₁ is switched off.

Each variable can be represented as their active and reactive components, orthogonal to each other. Further, after the algebraization procedure, we obtain a matrix (6) of (8) equations connected by a switching function.

$$\left|B\right|\left|A\right|=\left|C\right|,$$

(6)

$$\left|B\right|=\left|\begin{array}{cccccccc}1& 1& 0& 0& 0& 0& -\omega \cdot L_1& 0\\ 0& 0& -\omega \cdot L_1& 0& -1& -1& 0& 0\\ 0& -{\mathsf{\psi }}_{\sin }& 0& R/2& 0& 0& \omega \cdot L_1/2& \omega \cdot L_2/2\\ 0& 0& \omega \cdot L_1/2& \omega \cdot L_2/2& 0& {\mathsf{\psi }}_{\cos }& 0& -R/2\\ 0& 0& -1& 1& -\omega \cdot C_1& 0& 0& 0\\ -\omega \cdot C_1& 0& 0& 0& 0& 0& 1& -1\\ 1/2& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\sin }& 0& R/2& 0& 0& 0& \omega \cdot L_2/2\\ 0& 0& 0& \omega \cdot L_2/2& -1/2& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\cos }& 0& -R/2\end{array}\right|,$$

(7)

$$\left|A\right|={\left|\begin{array}{cccccccc}{U}_{C1a}& U_{C2a}& I_{3a}& I_{1a}& U_{C1r}& U_{C2r}& I_{3r}& I_{1r}\end{array}\right|}^T,$$

(8)

$$\left|C\right|={\left|0\hspace{1em}0\hspace{1em}{E}_a/2\hspace{1em}0\hspace{1em}0\hspace{1em}0\hspace{1em}{E}_a/2\hspace{1em}0\right|}^T.$$

(9)

The expression consists of three parts, where matrix B is a matrix of coefficients (7), matrix A is a vector column of variables (8), and matrix C is a vector column of input sources (9).

To obtain the resulting value of each variable, we perform (10)

$$X_{y(n)}=\sqrt{X_{y(n)a}^2+X_{y(n)r}^2},$$

(10)

where n is the harmonic number.

Next, the equations for all other schemes were obtained. For CC (11)–(13):

$$\left|B\right|=\left|\begin{array}{cccccc}{\mathsf{\psi }}_{\sin }& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\sin }& {\displaystyle \frac{R}{2}}& 0& 0& \omega \cdot L_2/2\\ 0& 0& \omega \cdot L_2/2& -{\mathsf{\psi }}_{\cos }& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\cos }& -{\displaystyle \frac{R}{2}}\\ 0& 0& 1/2& -\omega \cdot C_1\cdot {\mathsf{\psi }}_{\sin }& -{\displaystyle \frac{\omega \cdot C_2}{2}}+{\mathsf{\psi }}_{\sin }\cdot \omega \cdot C_2& 0\\ -\omega \cdot C_1\cdot {\mathsf{\psi }}_{\cos }& -{\displaystyle \frac{\omega \cdot C_2}{2}}+{\mathsf{\psi }}_{\cos }\cdot \omega \cdot C_2& 0& 0& 0& -1/2\\ {\mathsf{\psi }}_{\sin }& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\sin }& 0& 0& 0& 0\\ 0& 0& 0& -{\mathsf{\psi }}_{\cos }& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\cos }& 0\end{array}\right|,$$

(11)

$$\left|A\right|={\left|\begin{array}{cccccc}{U}_{C1a}& U_{C2a}& I_{1a}& U_{C1r}& U_{C2r}& I_{1r}\end{array}\right|}^T,$$

(12)

$$\left|C\right|={\left|\begin{array}{cccccc}{E}_a/2& 0& 0& 0& 0& 0\end{array}\right|}^T.$$

(13)

For the C controller (14)–(16):

$$\left|B\right|=\left|\begin{array}{cccccc}{\mathsf{\psi }}_{\sin }& {\displaystyle \frac{R_2}{2}}-{\mathsf{\psi }}_{\sin }\cdot R_2& {\displaystyle \frac{R}{2}}& 0& 0& \omega \cdot L_2/2\\ 0& 0& \omega \cdot L_2/2& -{\mathsf{\psi }}_{\cos }& -{\displaystyle \frac{R_2}{2}}+{\mathsf{\psi }}_{\cos }\cdot R_2& -{\displaystyle \frac{R}{2}}\\ 0& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\sin }& 1/2& -\omega \cdot C_1\cdot {\mathsf{\psi }}_{\sin }& 0& 0\\ -\omega \cdot C_1\cdot {\mathsf{\psi }}_{\cos }& 0& 0& 0& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\cos }& -1/2\\ {\mathsf{\psi }}_{\sin }& -{\displaystyle \frac{R_2}{2}}+{\mathsf{\psi }}_{\sin }\cdot R_2& 0& 0& 0& 0\\ 0& 0& 0& -{\mathsf{\psi }}_{\cos }& {\displaystyle \frac{R_2}{2}}-{\mathsf{\psi }}_{\cos }\cdot R_2& 0\end{array}\right|,$$

(14)

$$\left|A\right|={\left|\begin{array}{cccccc}{U}_{C1a}& I_{3a}& I_{1a}& U_{C1r}& I_{3r}& I_{1r}\end{array}\right|}^T,$$

(15)

$$\left|C\right|={\left|\begin{array}{cccccc}{E}_a/2& 0& 0& 0& 0& 0\end{array}\right|}^T.$$

(16)

And for a two-level LCC (17)–(19):

$$\begin{array}{l}\left|B\right|=\left|\begin{array}{ccccccc}R/2& 0& 0& 0& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\sin }& 0& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\sin }\\ \omega \cdot L/2& \omega \cdot L_{1x}/2& \omega \cdot L_{1y}/2& 0& 0& 0& 0\\ 0& 0& 0& 1& 1& 0& 0\\ 0& \omega \cdot L_{1x}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 1\\ 0& 0& \omega \cdot L_{1y}& 0& 0& 0& 0\\ R/2& 0& 0& -1/2& -{\mathsf{\psi }}_{\sin }& -1/2& -{\mathsf{\psi }}_{\sin }\\ \omega \cdot L/2& 0& 0& 0& 0& 0& 0\\ 1& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& \omega \cdot C_{1x}& 0& 0& 0\\ 0& 1/2& -{\mathsf{\psi }}_{\sin }& 0& 0& 0& 0\\ 0& 0& 0& 0& -\omega \cdot C_{2x}/2& {\mathsf{\psi }}_{\cos }\cdot \omega \cdot C_{1y}& 0\\ 0& 0& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\sin }& 0& 0& 0& 0\\ 0& 0& 0& -\omega \cdot C_{1x}/2& \omega \cdot C_{2x}/2& {\displaystyle \frac{\omega \cdot C_{1y}}{2}}-{\mathsf{\psi }}_{\cos }\cdot \omega \cdot C_{1y}& 0\end{array}\right.\\ \left.\begin{array}{ccccccc}\omega \cdot L/2& \omega \cdot L_{1x}/2& \omega \cdot L_{1y}/2& 0& 0& 0& 0\\ -R/2& 0& 0& 0& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\cos }& 0& -{\displaystyle \frac{1}{2}}+{\mathsf{\psi }}_{\cos }\\ 0& \omega \cdot L_{1x}& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& -1& 0& 0\\ 0& 0& \omega \cdot L_{1y}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -1& -1\\ \omega \cdot L/2& 0& 0& 0& 0& 0& 0\\ -R/2& 0& 0& 1/2& {\mathsf{\psi }}_{\cos }& 1/2& {\mathsf{\psi }}_{\cos }\\ 0& 0& 0& \omega \cdot C_{1x}& 0& 0& 0\\ -1& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -\omega \cdot C_{2x}/2& {\mathsf{\psi }}_{\sin }\cdot \omega \cdot C_{1y}& 0\\ 0& -1/2& {\mathsf{\psi }}_{\cos }& 0& 0& 0& 0\\ 0& 0& 0& -\omega \cdot C_{1x}/2& \omega \cdot C_{2x}/2& {\displaystyle \frac{\omega \cdot C_{1y}}{2}}-{\mathsf{\psi }}_{\sin }\cdot \omega \cdot C_{1y}& 0\\ 0& 0& {\displaystyle \frac{1}{2}}-{\mathsf{\psi }}_{\cos }& 0& 0& 0& 0\end{array}\right|\end{array},$$

(17)

$$\left|A\right|={\left|\begin{array}{cccccccccccccc}{I}_{1a}& I_{3xa}& I_{3ya}& U_{C1xa}& U_{C2xa}& U_{C1ya}& U_{C2ya}& I_{1r}& I_{3xr}& I_{3yr}& U_{C1xr}& U_{C2xr}& U_{C1yr}& U_{C2yr}\end{array}\right|}^T,$$

(18)

$$\left|C\right|={\left|\begin{array}{cccccccccccccc}{E}_a/2& 0& 0& 0& 0& 0& E_a/2& 0& 0& 0& 0& 0& 0& 0\end{array}\right|}^T.$$

(19)

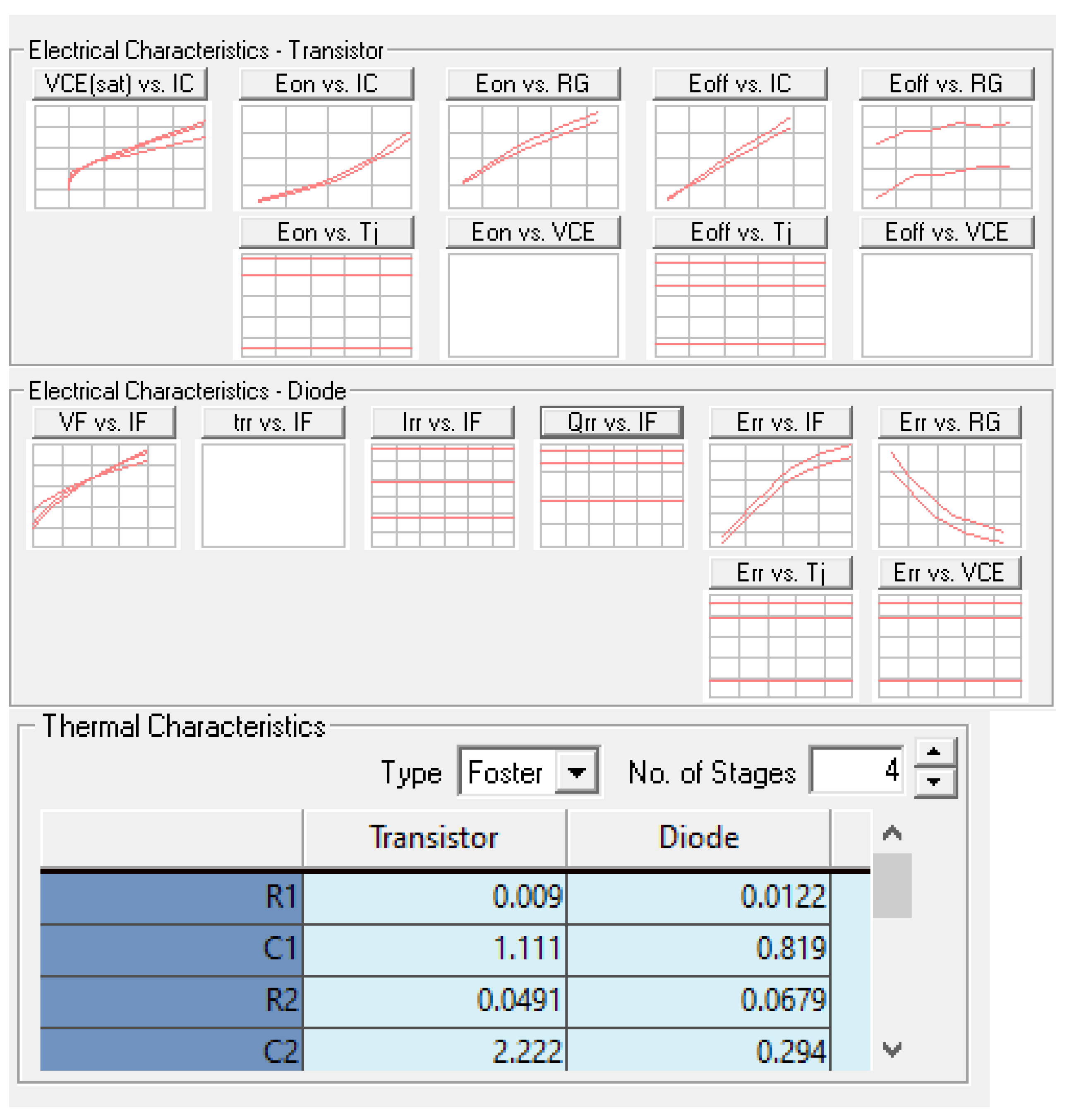
4. Simulation

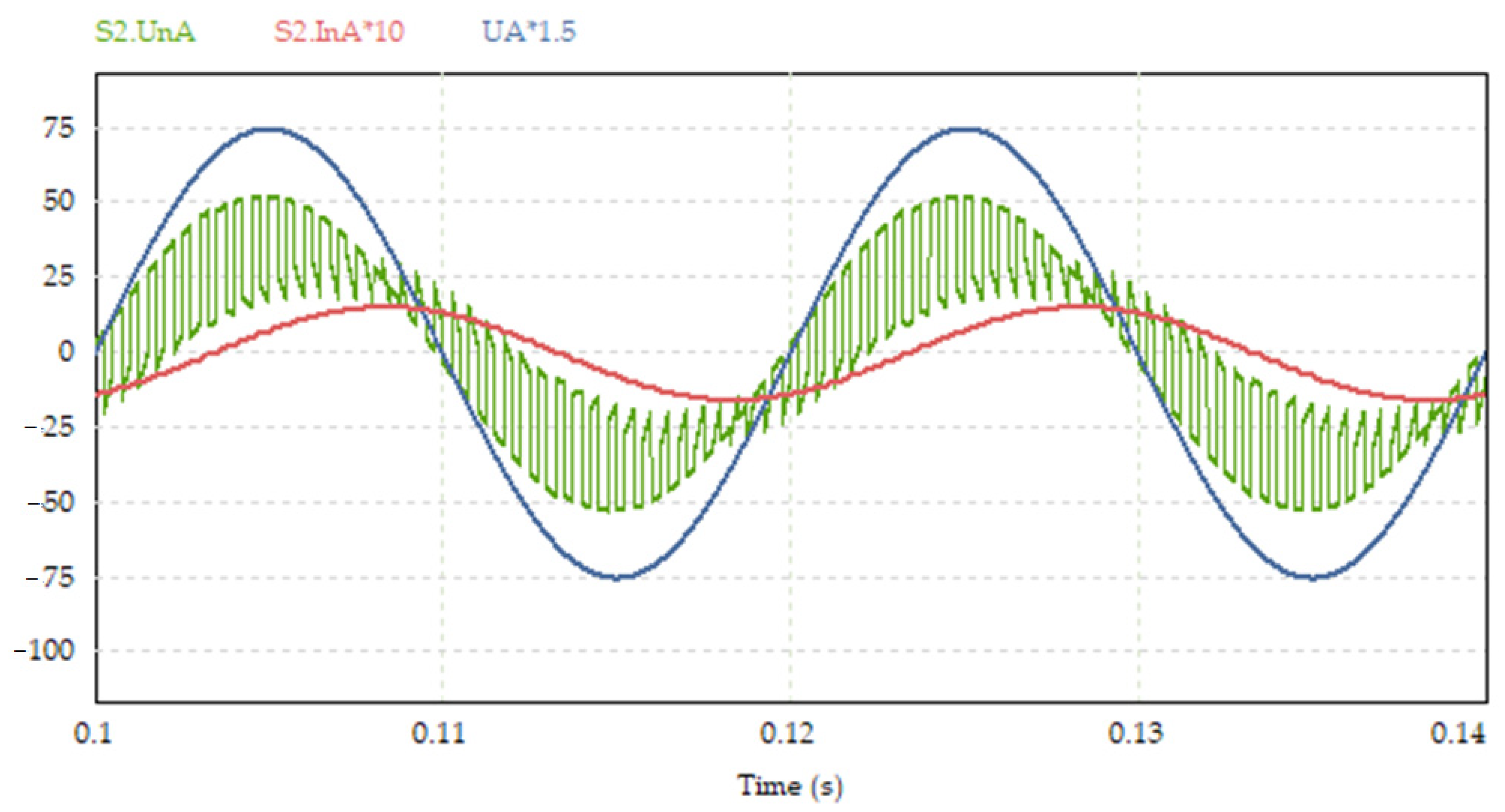
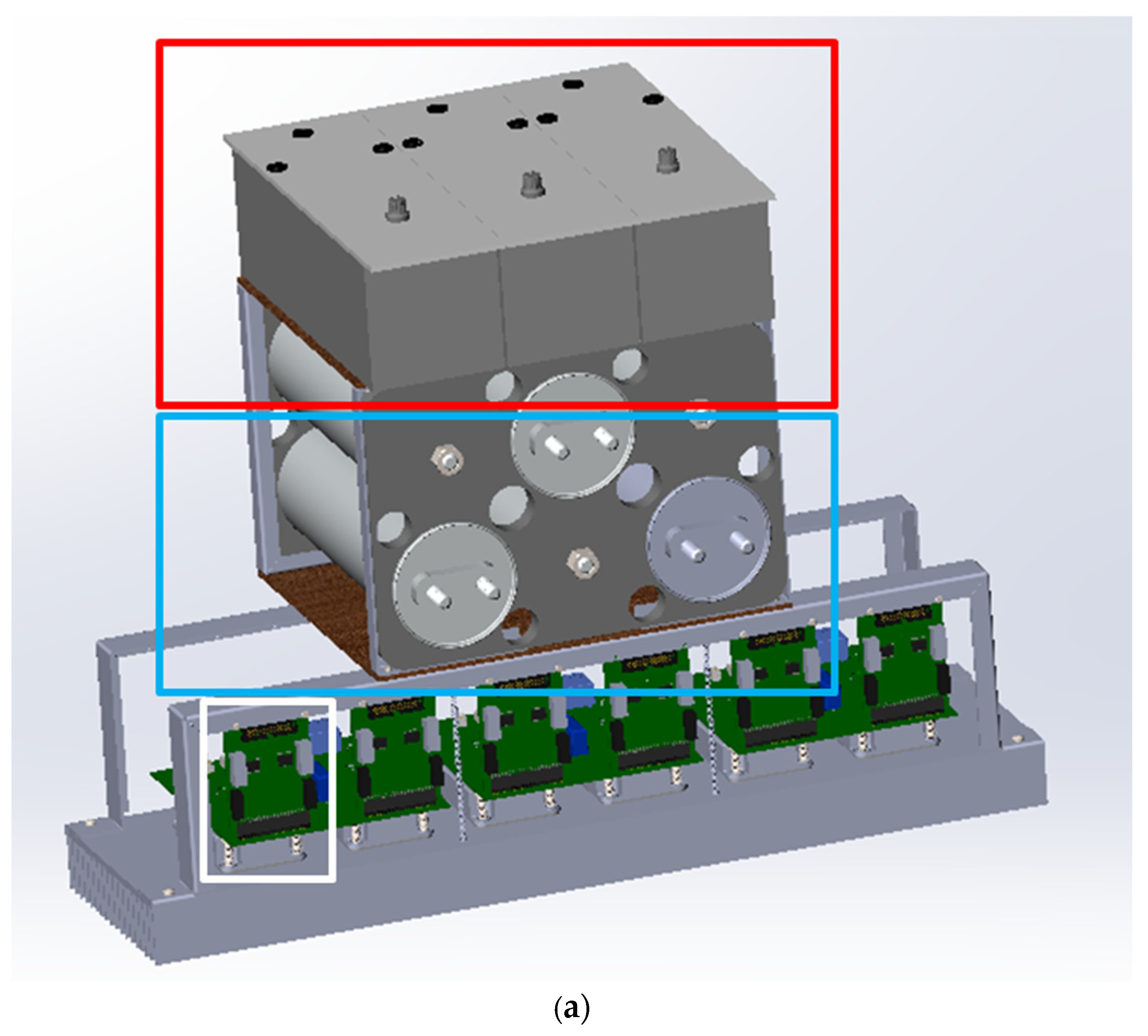
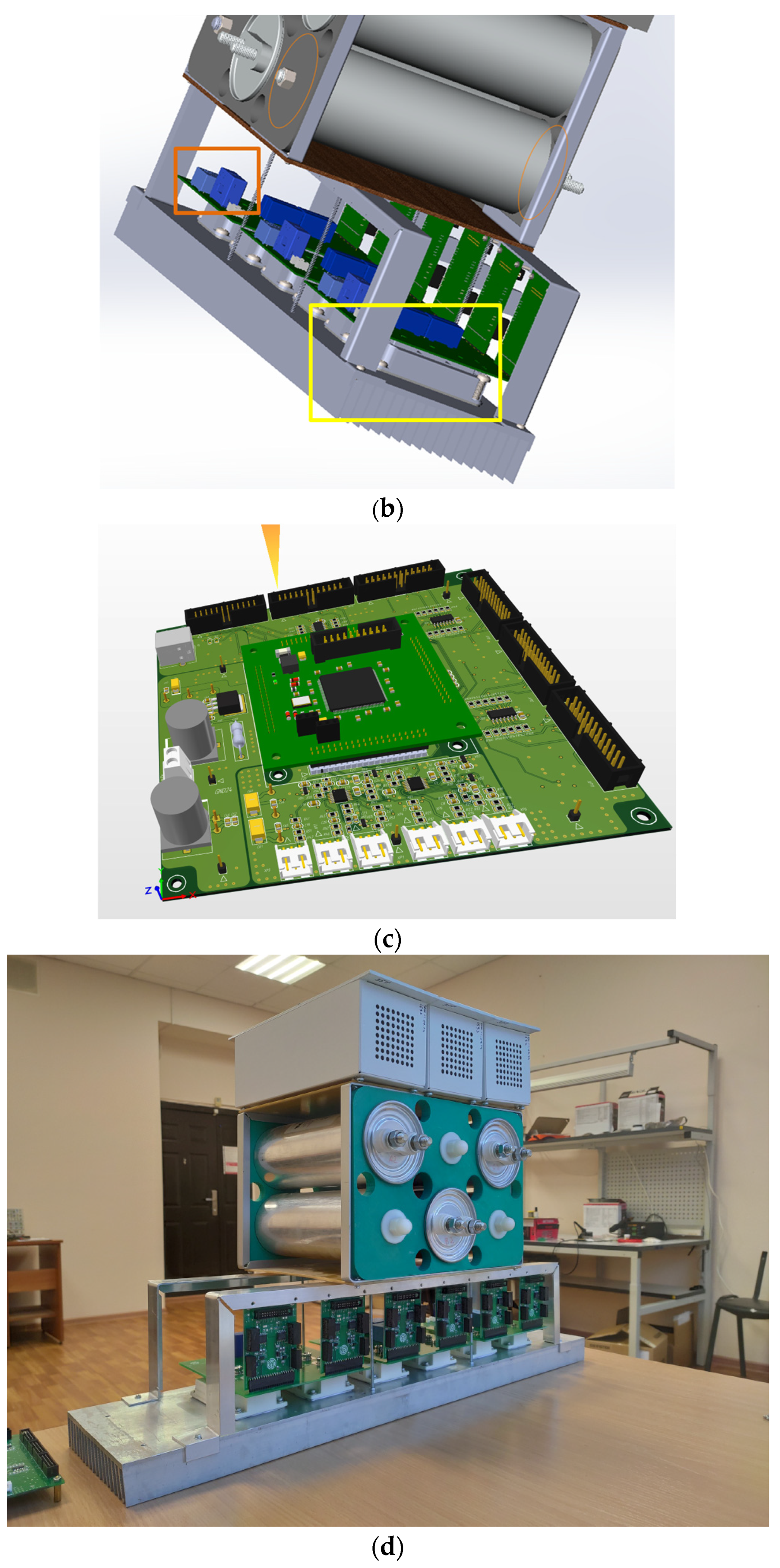
A family of buck-boost RAVs with phase-by-phase switches was simulated in PSIM. The simulation was performed using thermal models of transistors that were used in the experimental GD200CEY120C2S layout by STARPOWER. An example of setting parameters in the PSIM program is shown in Figure 2.

It is worth noting that the technical documentation provided parameters for the Foster-type model. The following parameters of the elements were taken for the study: throttle L₁ = 100 mH, capacitor C₁ = 100 uF, C₂ = 10 uF, the output load power reaches 2.5 kW at a supply voltage of 310 V and 65 W at a voltage of 50 V; 50 V was taken for the first reference point, with which the experiment will be performed. Nevertheless, all the obtained characteristics are given in relative units and are represented by the sign *. The output voltage is reduced to the input voltage, the output current to the base output current, which is defined as U_in divided by the input resistance.

Figure 3 shows the diagrams of the output voltage for the LCC RAV, combined with the input voltage and load current.

The control characteristics were obtained in Figure 4. The characteristics are combined for different types of regulators, and graphs are also presented, obtained by mathematical calculation for one version of the circuits; for the rest, they are similar.

According to the graph, it can be concluded that with different versions of the circuit, it is possible to achieve a full range of regulation where the maximum voltage is 1.6 times higher than the nominal one.

In turn, the load characteristics were obtained, as shown in Figure 5, with the corresponding circuit variants, as indicated above, the modulation depths of 0.0625 and 0.5 were taken as a test group.

At medium levels of modulation depths, a maximum load of the regulator exceeding two times is possible, whereas the maximum voltage level is reached only when the modulation depth is close to zero.

To study the effect of the AC voltage regulator on the supply network, the dependences of the input shift factor on the modulation depth were obtained, as shown in Figure 6.

Taking into account the active-inductive nature of the load, the input shift factor tends to unity in the LCC and C circuits.

The quality of the input current and output voltage was evaluated by their THD, as shown in Figure 7 for current and Figure 8 for voltage.

As can be seen from the graphs, the most effective regulators were two-level LCC, C, LCC in input current and CC, C, and LCC in output voltage.

In turn, an assessment of heat losses relative to the output in different versions of the schemes was made, which is shown in

Table 1. Assessment of heat losses.

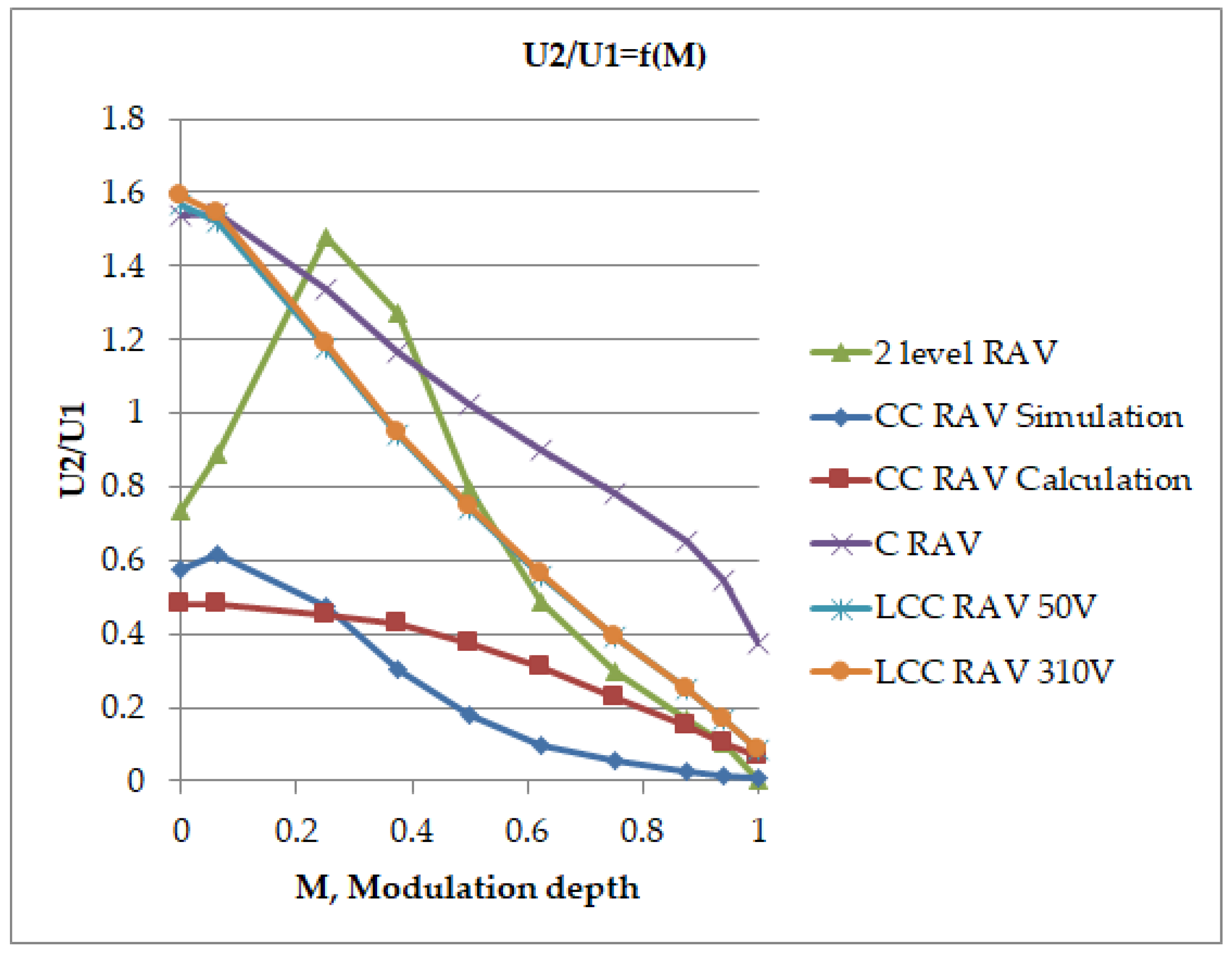
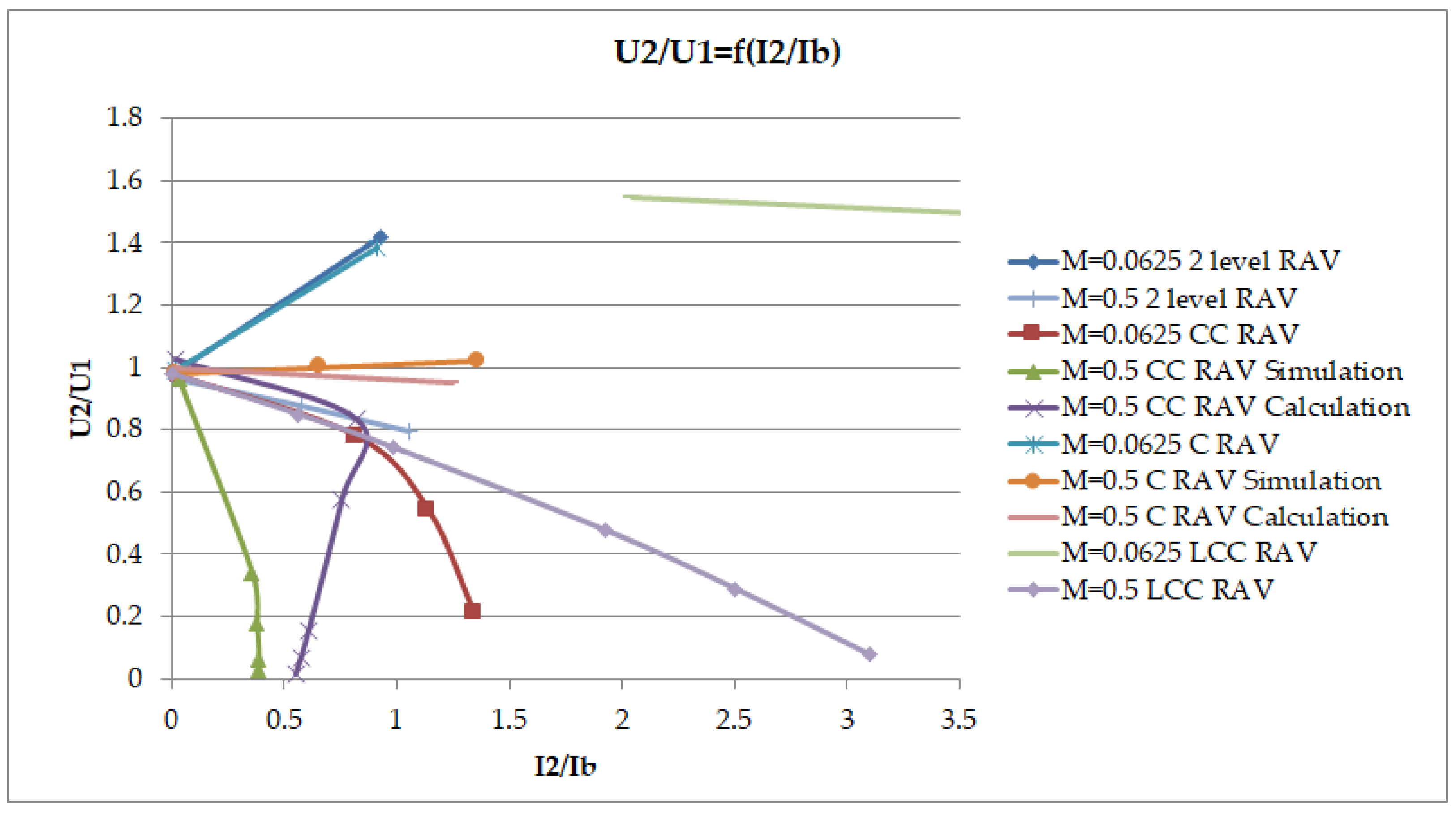
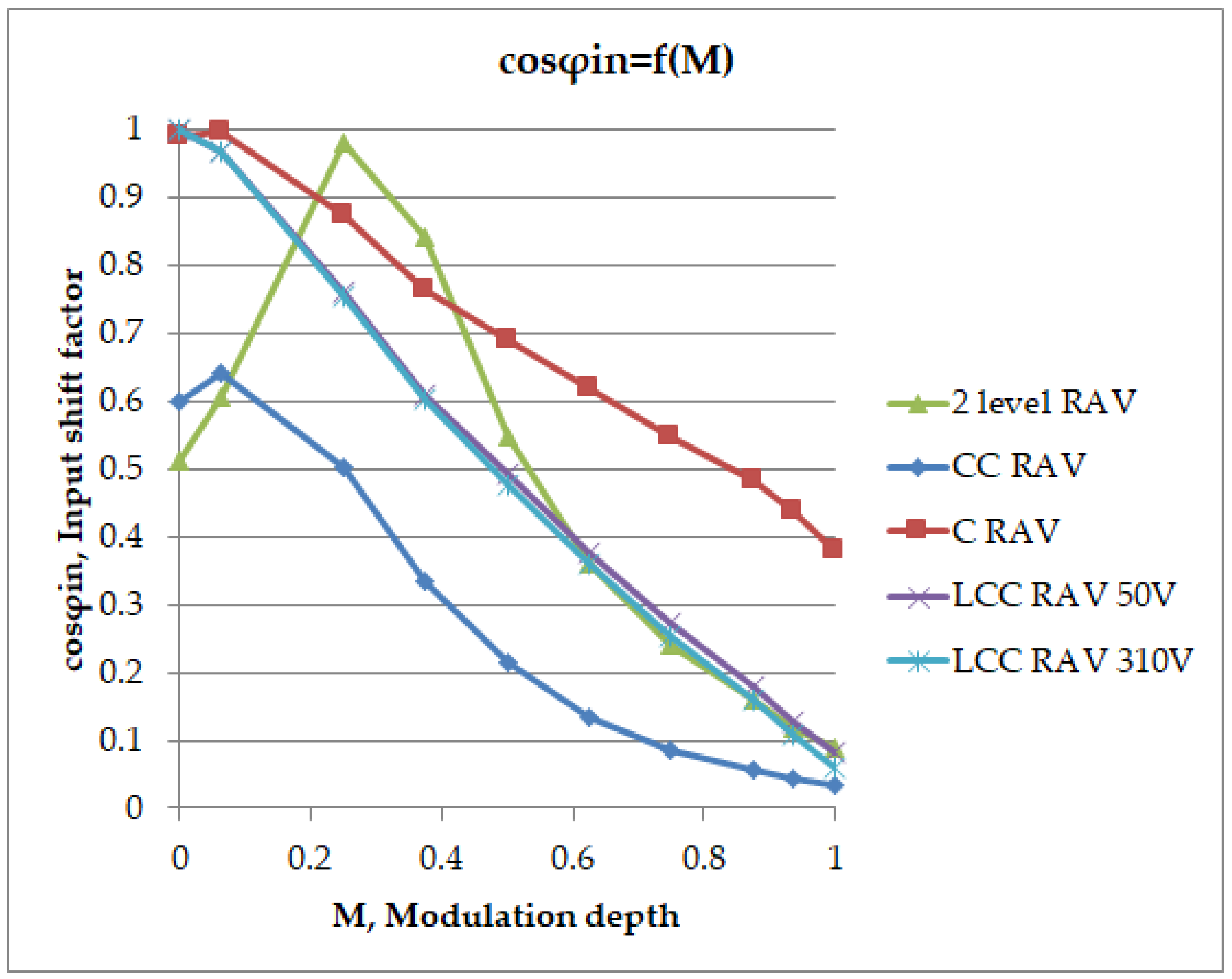
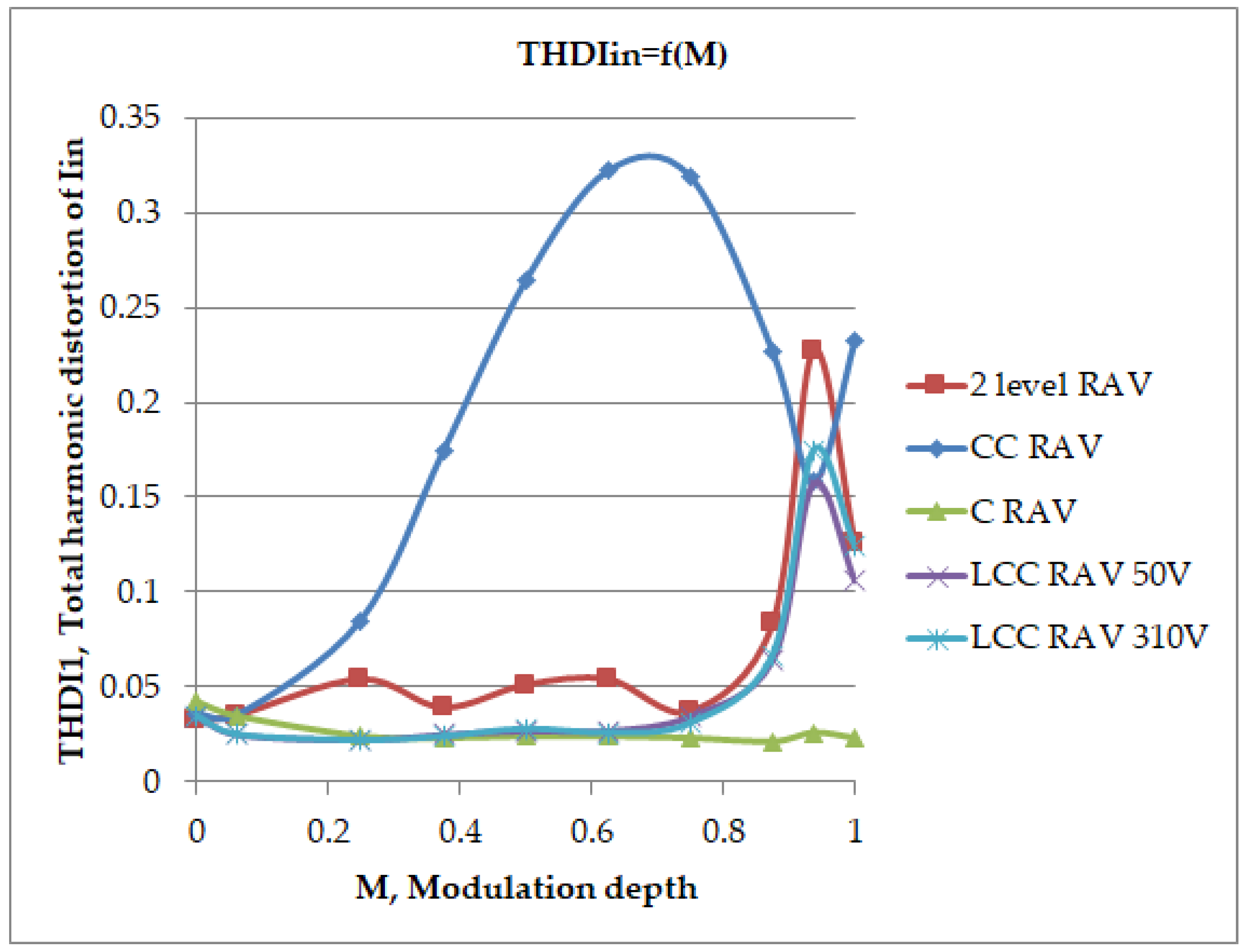
M/RAV Variants	LCC (50 V)	LCC (310 V)	C	CC	2 Level LCC
1	29%	8.7%	99%	82%	99%
0.9	21.7%	5.5%	8%	85%	49%
0.8	15.4%	3.7%	5.6%	76%	37%
0.7	10.1%	2.4%	4.5%	59%	25%
0.6	7.3%	1.7%	4%	41%	16.6%
0.5	5.5%	1.3%	3.5%	26%	10.4%
0.3	4.4%	1%	3.2%	16%	6.9%
0.2	3.5%	0.8%	2.9%	9.3%	6.1%
0.1	2.8%	0.6%	2.7%	5.5%	9.3%
0	2.2%	0.5%	2.2%	5.4%	9.4%

.

From this analysis, it can be concluded that LCC can be considered the most effective circuit, especially when operating at a voltage of 310 V, in this regard, the LCC RAV variant was chosen in the experiment.

5. Experiment

An experimental layout was assembled for the LCC RAV variant, as shown in Figure 9. The control system is currently being debugged and implemented through an observer. Also, this circuit was assembled earlier for testing on output elements (without printed circuit boards and IGBT modules); the results of the operation are shown in Figure 10.

6. Conclusions

A family of buck-boost RAVs with phase-by-phase switches is proposed. In these converters, it is possible to use IGBT transistors with counter-sequential switching of keys with a low switching frequency, up to 2 kHz, since the quality of the input current and output voltage is achieved due to the structure of the circuit and the control system of the regulator. This solution allows for an increased output voltage. The control range, depending on the circuit, can vary in the range from 0 to 1.6 times relative to the output voltage. Accordingly, it provides both a decrease and an increase in voltage. This device meets the requirements of a compensator for the asymmetry of the output voltage level of a three-phase network, and compensation is possible for both drawdowns and overvoltages up to 60%. The three-phase version of the RAV is obtained by connecting the output terminals of the load to a star. In turn, the regulator can be built according to a single-phase circuit, which may be relevant in private households. The quality of the input current remains high in the operating control range and does not exceed 0.05%, and the quality of the output voltage in the same section can be estimated by its harmonic coefficient not exceeding 0.6%. These indicators are significantly better (lower) than those of the CC variant of the scheme. The input shift factor is also close to one at the operating range, from which it can be seen that the regulator does not introduce an additional reactive component into the supply network, which indicates high electromagnetic compatibility.

In turn, an experimental layout was assembled, and the control system is currently being configured, which includes a voltage and current monitoring system.