DC Charging Capabilities of Battery-Integrated Modular Multilevel Converters Based on Maximum Tractive Power
Abstract
:1. Introduction
Contributions and Outline
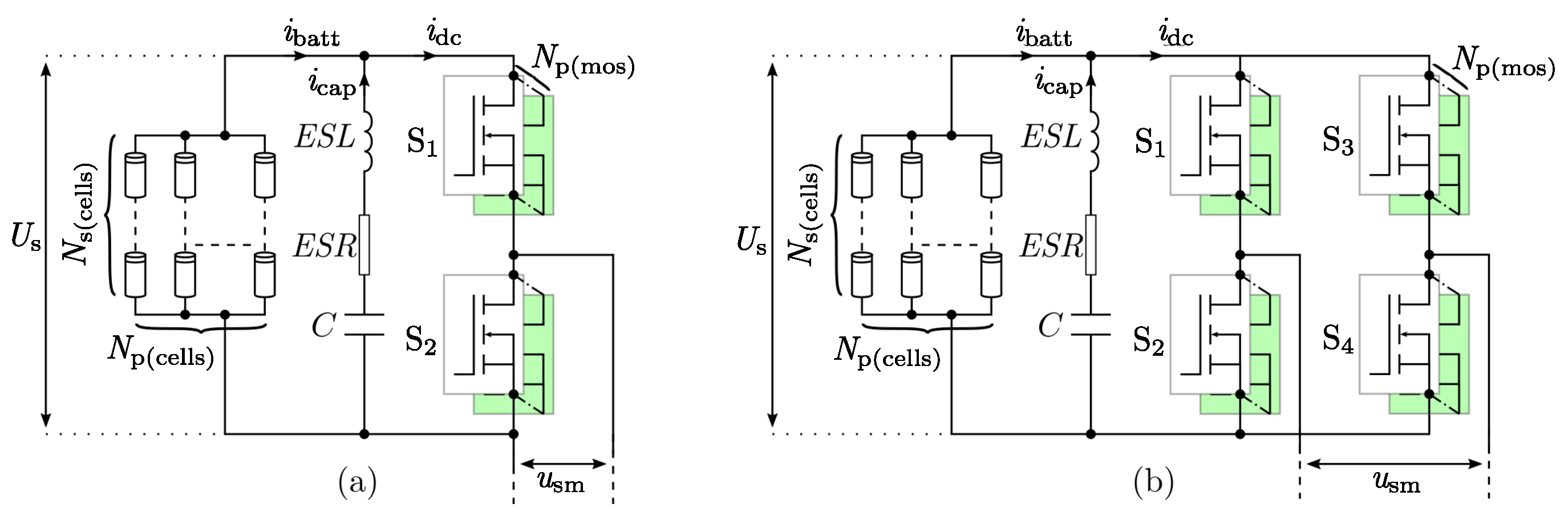
2. Topology Review
3. Total Number of Submodules
3.1. CDC-T: Total Number of Submodules Determined by the Traction Voltage
3.2. CDC-C: Total Number of Submodules Determined by Maximum DC Charger Voltage
4. Power Loss Calculations
4.1. Power Loss during Traction
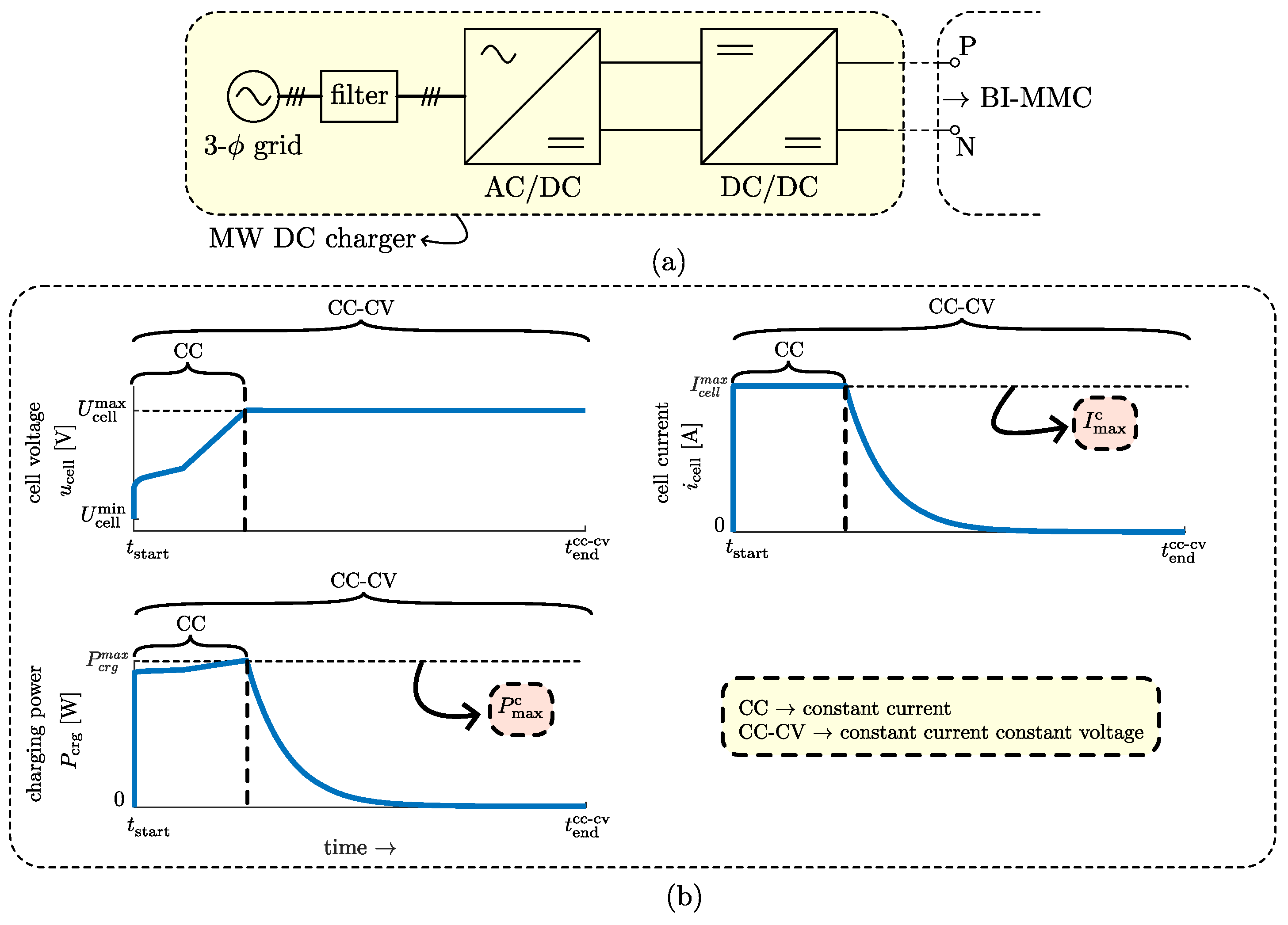
4.2. Power Loss during DC Charging
5. Maximum DC Charging Power Calculations
6. Submodule Case Temperature
7. Comparative Assessment
7.1. Number of Submodules
7.1.1. Ns(cells) Comparison
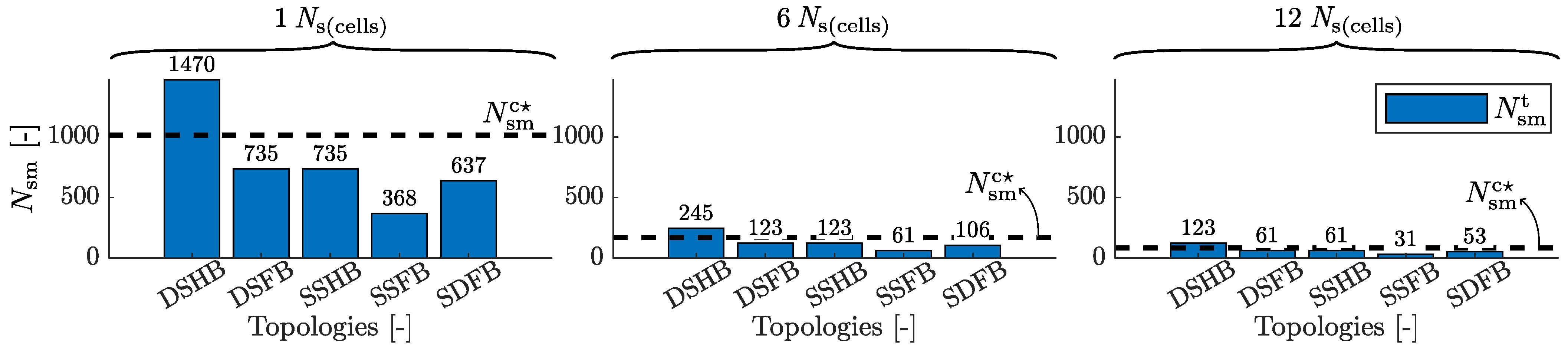
7.1.2. Topology Comparison
7.2. Submodule Losses
7.2.1. Ns(cells) Comparison
7.2.2. Topology Comparison
7.3. Total Semiconductor Losses
7.3.1. Ns(cells) Comparison
7.3.2. Topology Comparison
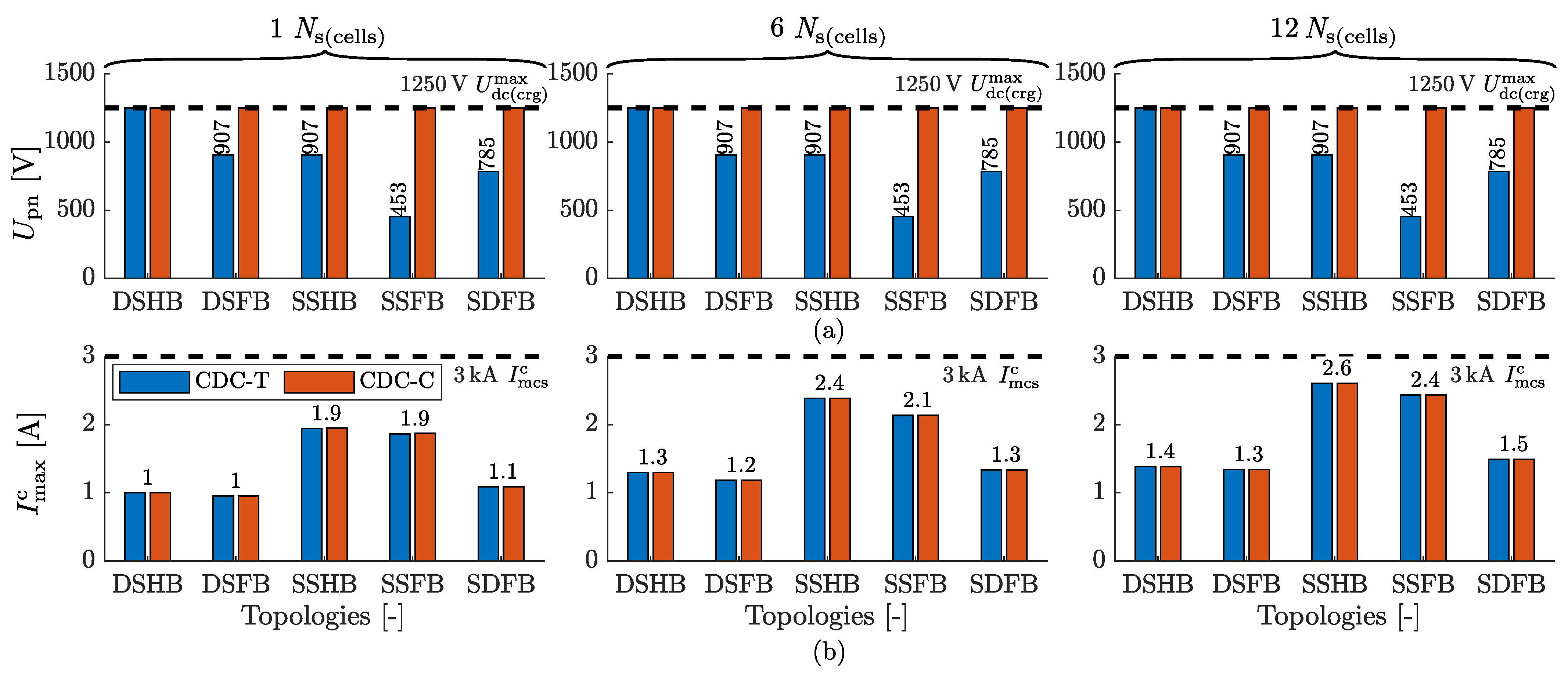
7.4. Maximum DC Charging Voltage and Current
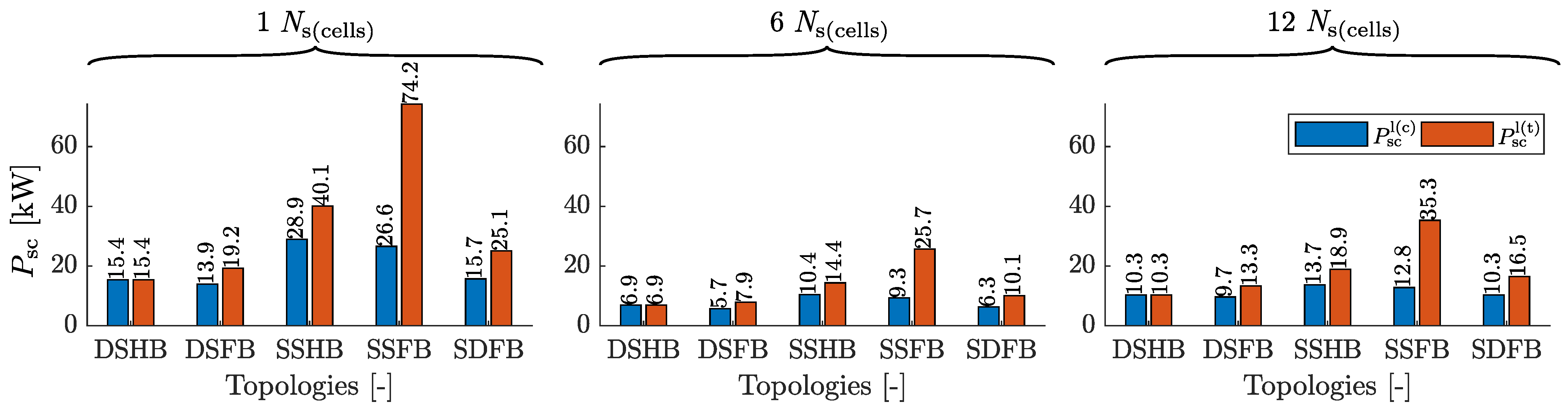
7.5. Maximum DC Charging Power
7.5.1. Ns(cells) Comparison
7.5.2. Topology Comparison
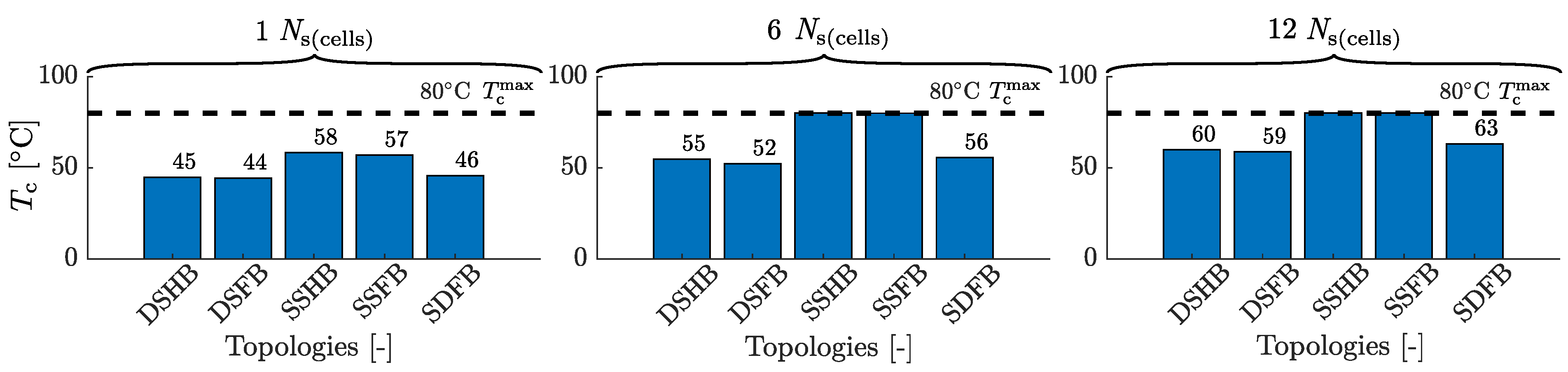
7.6. Submodule Temperature
7.6.1. Ns(cells) Comparison
7.6.2. Topologies Comparison
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Topology / Ns(cells) | 1 | 6 | 12 |
|---|---|---|---|
| Total number of parallel MOSFETs (Np(mos)) | |||
| DSHB | 4 | 4 | 4 |
| DSFB | 4 | 4 | 4 |
| SSHB | 4 | 5 | 6 |
| SSFB | 4 | 4 | 5 |
| SDFB | 4 | 4 | 4 |
| Maximum MOSFET on-state resistance () | |||
| - | 0.375 m | 0.6 m | 1.6 m |
| MOSFET switching frequency during traction () | |||
| DSHB | 4.2 kHz | 7.5 kHz | 9.8 kHz |
| DSFB | 2.5 kHz | 5.2 kHz | 8.8 kHz |
| SSHB | 3.2 kHz | 5.5 kHz | 7.5 kHz |
| SSFB | 1.8 kHz | 3.5 kHz | 6.2 kHz |
| SDFB | 2.2 kHz | 4.8 kHz | 8.2 kHz |
| SM case-to-ambient thermal resistance (Rca) | |||
| DSHB | 0.46 K/W | 0.52 K/W | 0.24 K/W |
| DSFB | 0.23 K/W | 0.27 K/W | 0.12 K/W |
| SSHB | 0.46 K/W | 0.52 K/W | 0.24 K/W |
| SSFB | 0.23 K/W | 0.27 K/W | 0.12 K/W |
| SDFB | 0.23 K/W | 0.27 K/W | 0.12 K/W |
References
- Mamalis, A.; Spentzas, K.; Mamali, A. The impact of automotive industry and its supply chain to climate change: Somme techno-economic aspects. Eur. Transp. Res. Rev. 2013, 5, 1–10. [Google Scholar] [CrossRef]
- Bonfils, C.J.; Santer, B.D.; Fyfe, J.C.; Marvel, K.; Phillips, T.J.; Zimmerman, S.R. Human influence on joint changes in temperature, rainfall and continental aridity. Nat. Clim. Chang. 2020, 10, 726–731. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Applications of Lithium-Ion Batteries in Electric Drive Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Plett, G.L. Battery Management Systems, Volume II: Equivalent-Circuit Methods; Artech House: Norwood, MA, USA, 2015. [Google Scholar]
- Berg, H. Batteries for Electric Vehicles: Materials and Electrochemistry; Cambridge University Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Li, Y.; Han, Y. A module-integrated distributed battery energy storage and management system. IEEE Trans. Power Electron. 2016, 31, 8260–8270. [Google Scholar] [CrossRef]
- Lin, C.H.; Chao, H.Y.; Wang, C.M.; Hung, M.H. Battery management system with dual-balancing mechanism for LiFePO4 battery module. In Proceedings of the TENCON 2011 IEEE Region 10 Conference, Bali, Indonesia, 21–24 November 2011; pp. 863–867. [Google Scholar]
- Estima, J.O.; Cardoso, A.J.M. Efficiency analysis of drive train topologies applied to electric/hybrid vehicles. IEEE Trans. Veh. Technol. 2012, 61, 1021–1031. [Google Scholar] [CrossRef]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A review of modulation and control techniques for multilevel inverters in traction applications. IEEE Access 2021, 9, 24187–24204. [Google Scholar] [CrossRef]
- Han, W.; Wik, T.; Kersten, A.; Dong, G.; Zou, C. Next-generation battery management systems: Dynamic reconfiguration. IEEE Ind. Electron. Mag. 2020, 14, 20–31. [Google Scholar] [CrossRef]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, pp. 1–6. [Google Scholar]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Trintis, I.; Munk-Nielsen, S.; Teodorescu, R. A new modular multilevel converter with integrated energy storage. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 1075–1080. [Google Scholar]
- Ota, J.I.Y.; Sato, T.; Akagi, H. Enhancement of performance, availability, and flexibility of a battery energy storage system based on a modular multilevel cascaded converter (MMCC-SSBC). IEEE Trans. Power Electron. 2015, 31, 2791–2799. [Google Scholar] [CrossRef]
- Lachichi, A. On modular multilevel converters-based batteries energy storage systems. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, Australia, 9–12 June 2015; pp. 908–912. [Google Scholar]
- Reniers, J.M.; Mulder, G.; Ober-Blöbaum, S.; Howey, D.A. Improving optimal control of grid-connected lithium-ion batteries through more accurate battery and degradation modelling. J. Power Sources 2018, 379, 91–102. [Google Scholar] [CrossRef]
- Bouchhima, N.; Gossen, M.; Birke, K.P. Fundamental Aspects of Reconfigurable Batteries: Efficiency Enhancement and Lifetime Extension. In Modern Battery Engineering: A Comprehensive Introduction; World Scientific Publishing Company: Singapore, 2019; p. 101. [Google Scholar]
- Bouchhima, N.; Gossen, M.; Schulte, S.; Birke, K.P. Lifetime of self-reconfigurable batteries compared with conventional batteries. J. Energy Storage 2018, 15, 400–407. [Google Scholar] [CrossRef]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and control of modular multilevel converters for battery electric vehicles. IEEE Trans. Power Electron. 2015, 31, 507–517. [Google Scholar] [CrossRef]
- Kersten, A.; Kuder, M.; Grunditz, E.; Geng, Z.; Wikner, E.; Thiringer, T.; Weyh, T.; Eckerle, R. Inverter and battery drive cycle efficiency comparisons of chb and mmsp traction inverters for electric vehicles. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–12. [Google Scholar]
- Josefsson, O. Investigation of a Multilevel Inverter for Electric Vehicle Applications. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2015. [Google Scholar]
- Wang, D.; Liu, J.; Piegari, L.; Song, S.; Chen, X.; De Simone, D. A Battery Lifetime Improved Control Strategy of Modular Multilevel Converter for Electric Vehicle Application. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 594–598. [Google Scholar]
- Ma, Y.; Lin, H.; Wang, X.; Wang, Z.; Ze, Z. Analysis of battery fault tolerance in modular multilevel converter with integrated battery energy storage system. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. 1–8. [Google Scholar]
- Tsirinomeny, M.; Rufer, A. Configurable modular multilevel converter (CMMC) for flexible EV. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Martel, T.; Rufer, A. Electric vehicle driving and fast charging system based on configurable modular multilevel converter (CMMC). In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Buberger, J.; Kersten, A.; Kuder, M.; Singer, A.; Mashayekh, A.; Estaller, J.; Thiringer, T.; Eckerle, R.; Weyh, T. Charging strategy for battery electric vehicles with a battery modular multilevel management (bm3) converter system using a pr controller. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar]
- Buberger, J.; Estaller, J.; Grupp, W.; Schwitzgebel, F.; Wiedenmann, A.; Mashayekh, A.; Kuder, M.; Eckerle, R.; Weyh, T. AC and DC Charging for Electric Vehicles with a Battery Modular Multilevel Management (BM3) Converter System. In Proceedings of the PCIM Europe 2022: International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2022; pp. 1–8. [Google Scholar]
- Ahmad, A.; Qin, Z.; Wijekoon, T.; Bauer, P. An Overview on Medium Voltage Grid Integration of Ultra-fast Charging Stations: Current Status and Future Trends. IEEE Open J. Ind. Electron. Soc. 2022, 3, 420–447. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme fast charging of electric vehicles: A technology overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- IEC 61851-1; Electric Vehicle Conductive Charging System-Part 1: General Requirements. IEC: Geneva, Switzerland, 2010; pp. 1–99.
- Suarez, C.; Martinez, W. Fast and ultra-fast charging for battery electric vehicles–a review. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 569–575. [Google Scholar]
- Smith, D.; Ozpineci, B.; Graves, R.L.; Jones, P.; Lustbader, J.; Kelly, K.; Walkowicz, K.; Birky, A.; Payne, G.; Sigler, C.; et al. Medium-And Heavy-Duty Vehicle Electrification: An Assessment of Technology and Knowledge Gaps; Technical Report; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2020. [Google Scholar]
- Meintz, A.; Starke, M.; Bohn, T. Charging Infrastructure Technologies: Development of a Multiport, > 1 MW Charging System for Medium-and Heavy-Duty Electric Vehicles; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2022. [Google Scholar]
- Industry Experts, Researchers Put Charging Systems for Electric Trucks to the Test—nrel.gov. Available online: https://www.nrel.gov/news/program/2021/industry-experts-researchers-put-charging-systems-for-electric-trucks-to-test.html (accessed on 21 November 2022).
- Balachandran, A. Battery-Integrtated Modular Multilevel Converter Topologies for Automotive Applications. Ph.D. Thesis, Linköping University, Linköping, Sweden, 2023. [Google Scholar] [CrossRef]
- Balachandran, A.; Jonsson, T.; Eriksson, L. Design and Analysis of Battery-Integrated Modular Multilevel Converters for Automotive Powertrain Applications. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Online, 6–10 September 2021; pp. 1–12. [Google Scholar]
- Starke, M.; Moorthy, R.S.K.; Adib, A.; Dean, B.; Chinthavali, M.; Xiao, B.; Campbell, S. A MW scale charging architecture for supporting extreme fast charging of heavy-duty electric vehicles. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 485–490. [Google Scholar]
- Moorthy, R.; Starke, M.; Dean, B.; Adib, A.; Campbell, S.; Chinthavali, M. Megawatt Scale Charging System Architecture. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Makoschitz, M. Multi-megawatt charging to foster the mobility transition. In e & i Elektrotechnik und Informationstechnik; Springer: London, UK, 2022; pp. 1–3. [Google Scholar]
- CharIN. CharIN Whitepaper Megawatt Charging System (MCS). 2022. Available online: https://www.charin.global/media/pages/technology/knowledge-base/c708ba3361-1670238823/whitepaper_megawatt_charging_system_1.0.pdf (accessed on 23 January 2023).



| Parameters | Symbol | Value |
|---|---|---|
| Maximum tractive power | 400 kW | |
| AC phase-to-phase voltage | Uv | 440 V |
| Electric machine nominal speed | - | 1000 rpm |
| Load power factor | 0.9 | |
| Maximum modulation index | Mmax | 0.85 |
| MCS DC charging voltage † | 1250 V | |
| MCS DC charging current † | 3000 A | |
| MOSFET CDC switching frequency | CDC– | ≈1 mHz |
| Total energy stored in the batteries | Ebatt | 1 MWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balachandran, A.; Jonsson, T.; Eriksson, L. DC Charging Capabilities of Battery-Integrated Modular Multilevel Converters Based on Maximum Tractive Power. Electricity 2023, 4, 62-77. https://doi.org/10.3390/electricity4010005
Balachandran A, Jonsson T, Eriksson L. DC Charging Capabilities of Battery-Integrated Modular Multilevel Converters Based on Maximum Tractive Power. Electricity. 2023; 4(1):62-77. https://doi.org/10.3390/electricity4010005
Chicago/Turabian StyleBalachandran, Arvind, Tomas Jonsson, and Lars Eriksson. 2023. "DC Charging Capabilities of Battery-Integrated Modular Multilevel Converters Based on Maximum Tractive Power" Electricity 4, no. 1: 62-77. https://doi.org/10.3390/electricity4010005
APA StyleBalachandran, A., Jonsson, T., & Eriksson, L. (2023). DC Charging Capabilities of Battery-Integrated Modular Multilevel Converters Based on Maximum Tractive Power. Electricity, 4(1), 62-77. https://doi.org/10.3390/electricity4010005







