Intrinsic Characteristics of Forward Simulation Modeling Electric Vehicle for Energy Analysis
Abstract
:1. Introduction
- Highlighting the intrinsic characteristics of the forward method;
- Providing a systematic description of the blocks involved, together with their equations and necessary considerations for the development of the model;
- Modeling, simulation, and validation of an electric vehicle by the forward method;
- Energy analysis of the electric vehicle before an Urban Dynamometer Driving Schedule (UDDS) driving cycle.
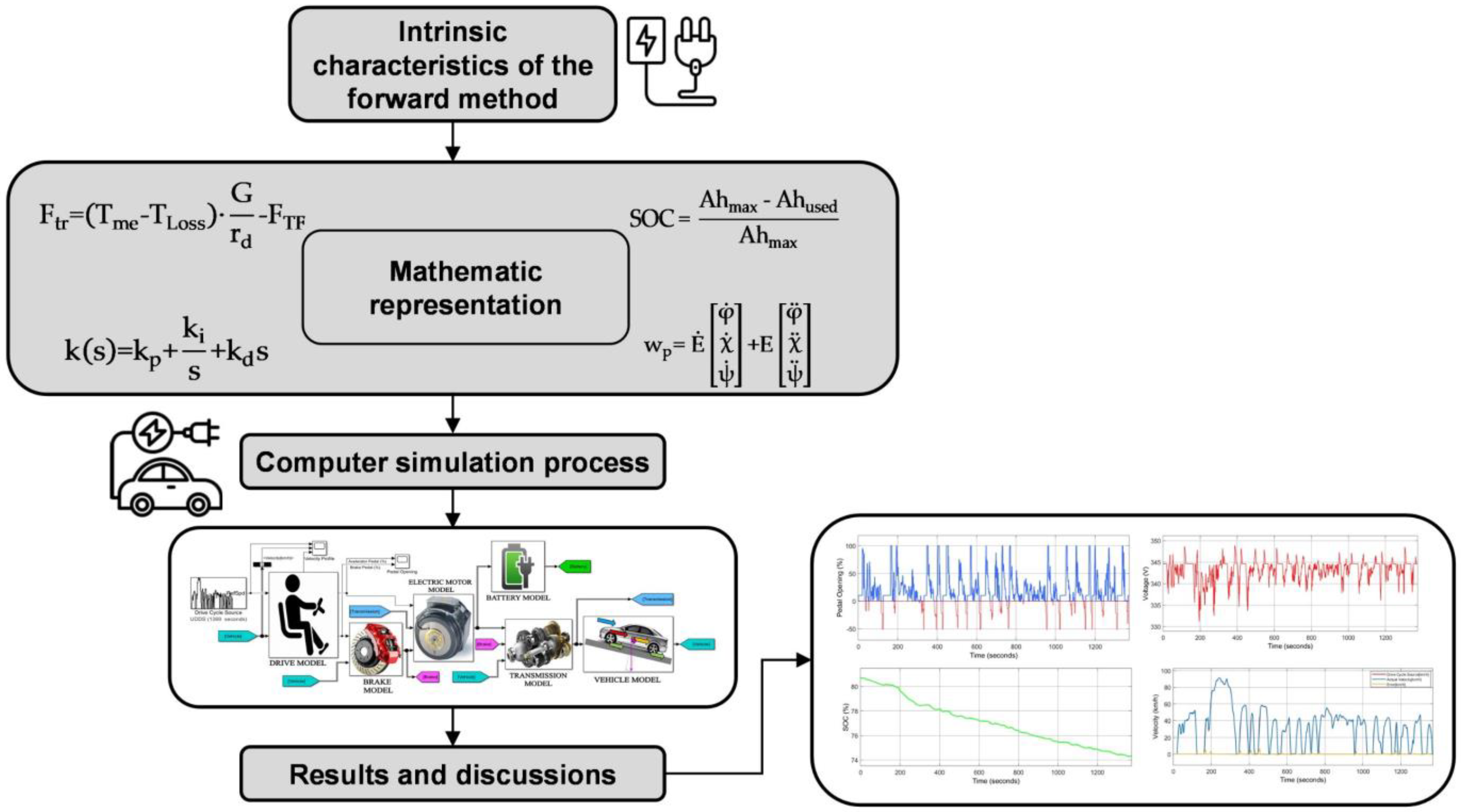
2. Materials and Methods
2.1. Background
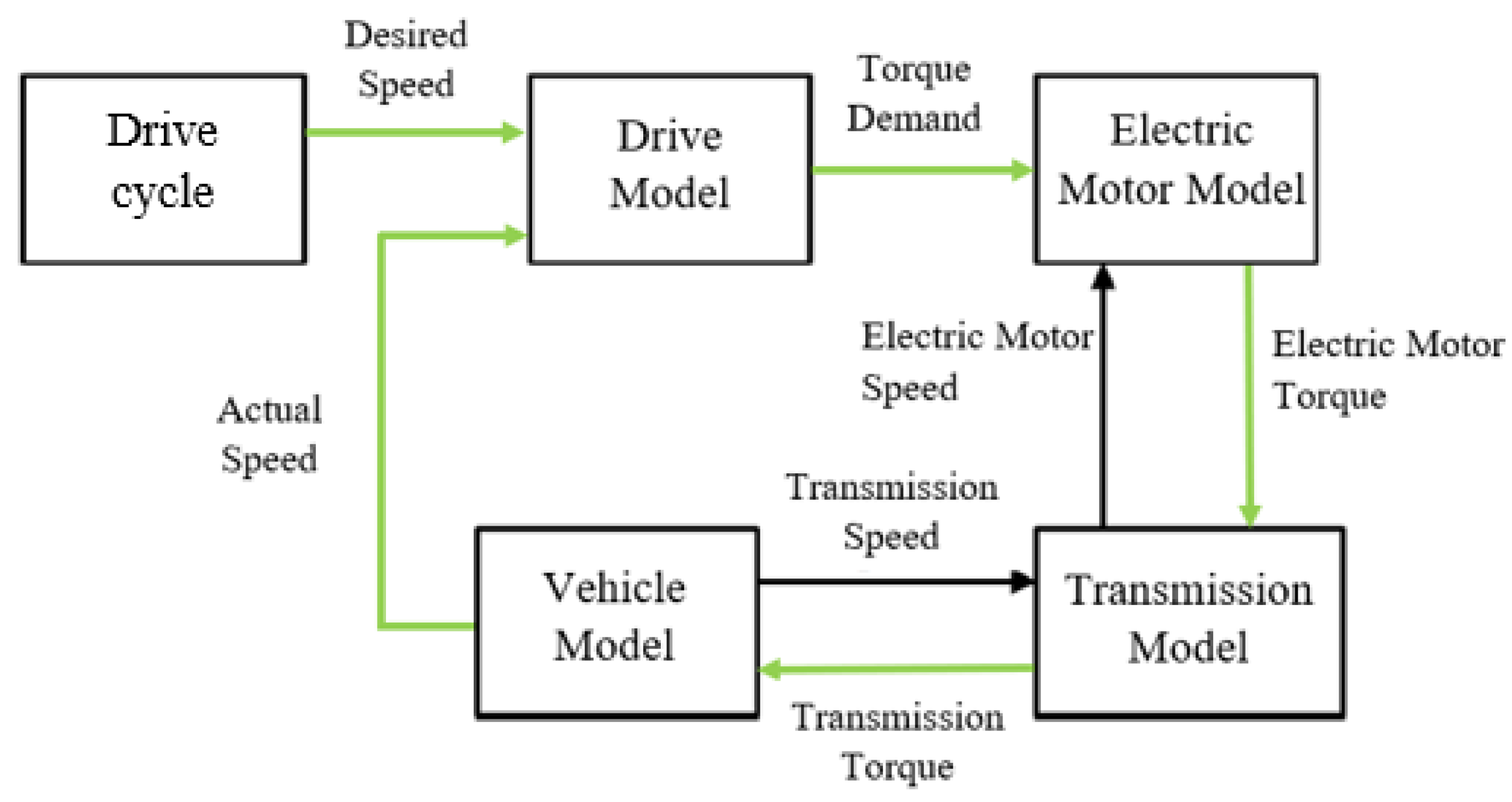
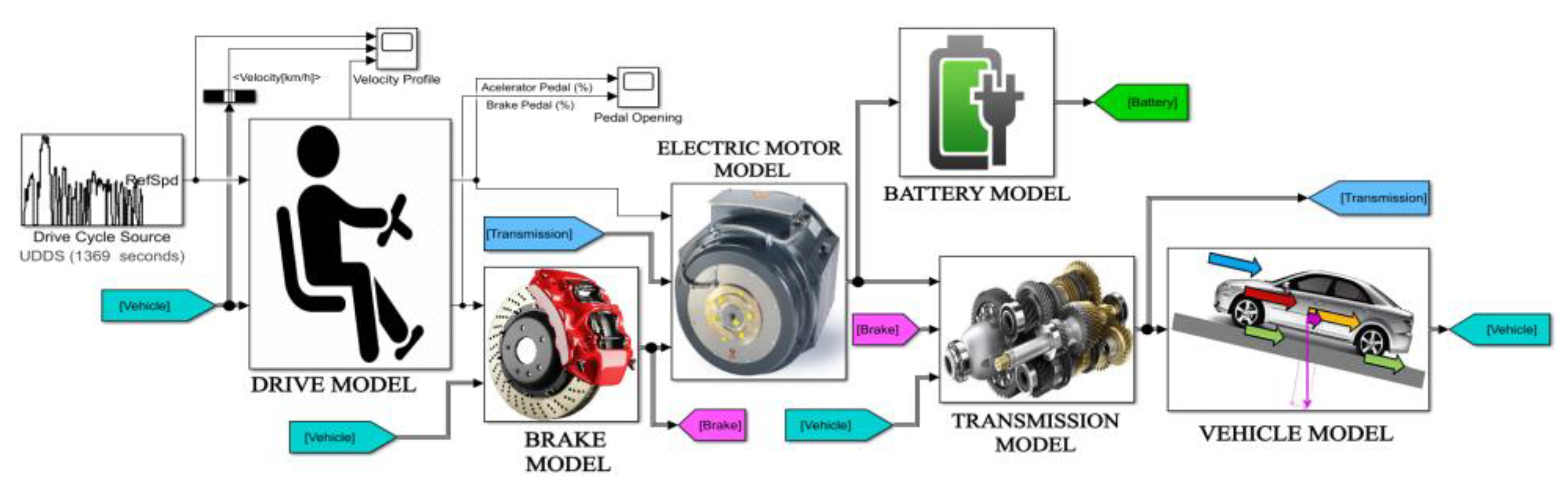
2.2. Mathematical Modeling of the Forward Method
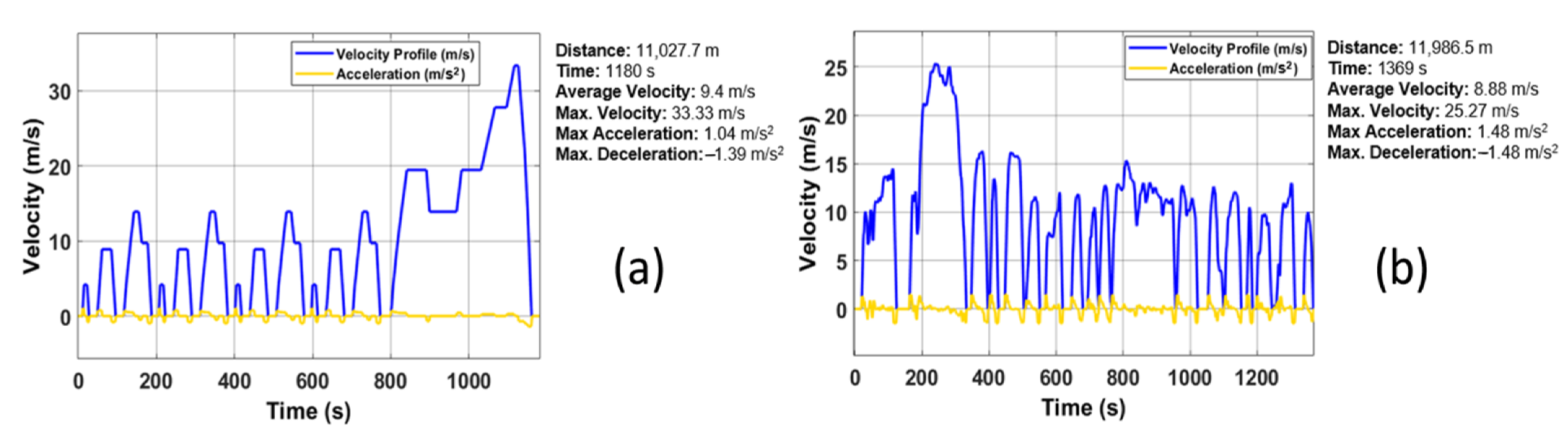
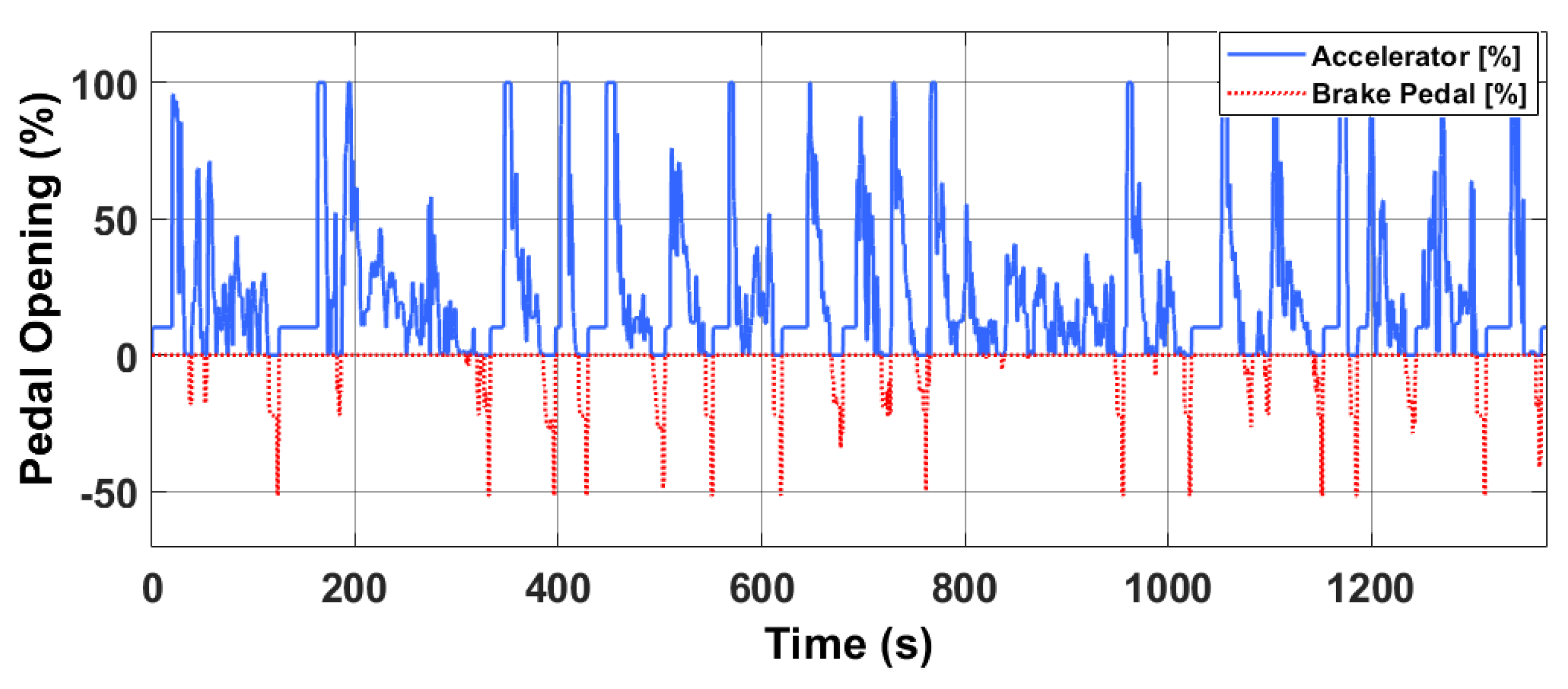
2.2.1. Driving Cycle Model
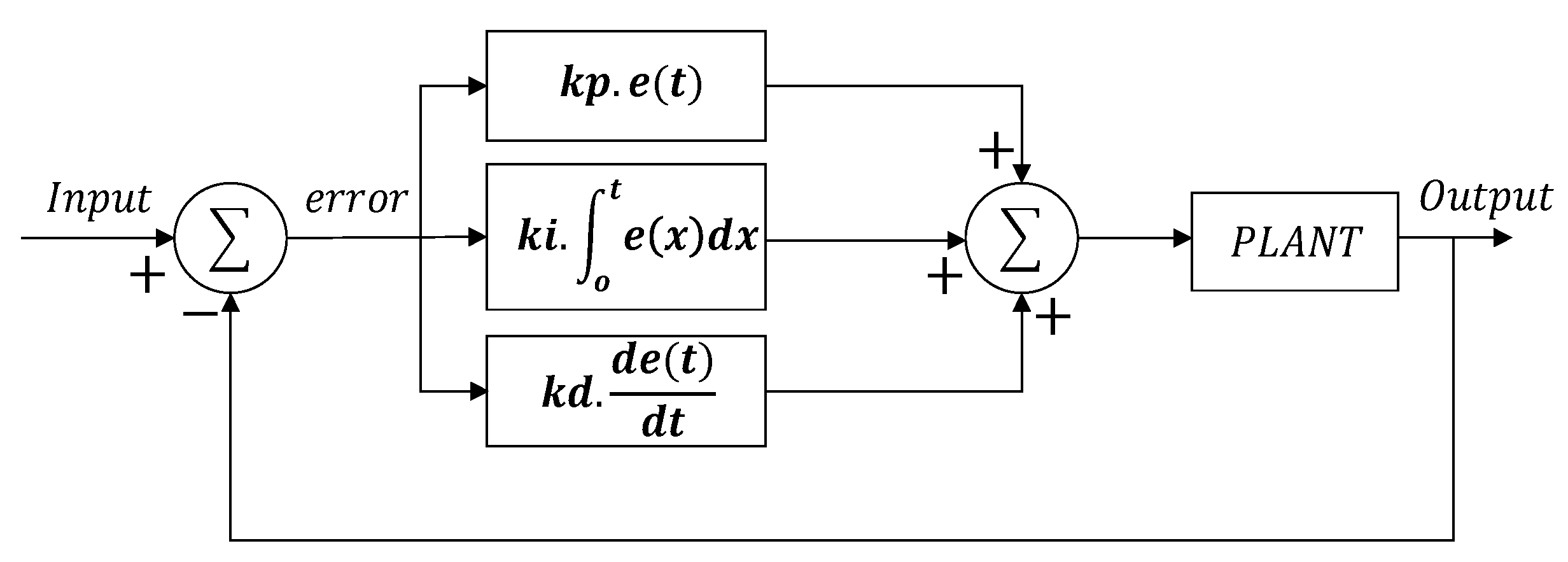
2.2.2. Driver Model
2.2.3. Brake Model
2.2.4. Electric Motor Model
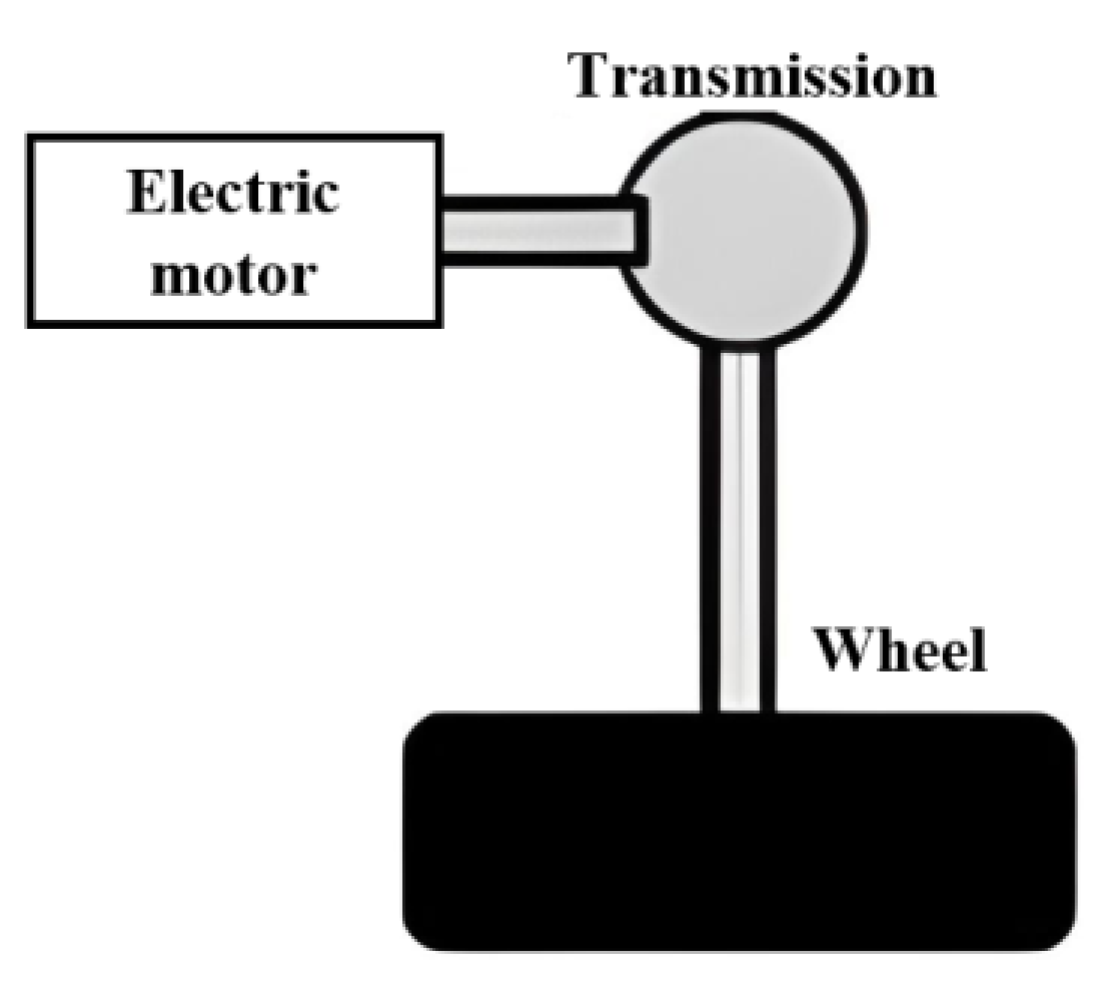
2.2.5. Transmission Model
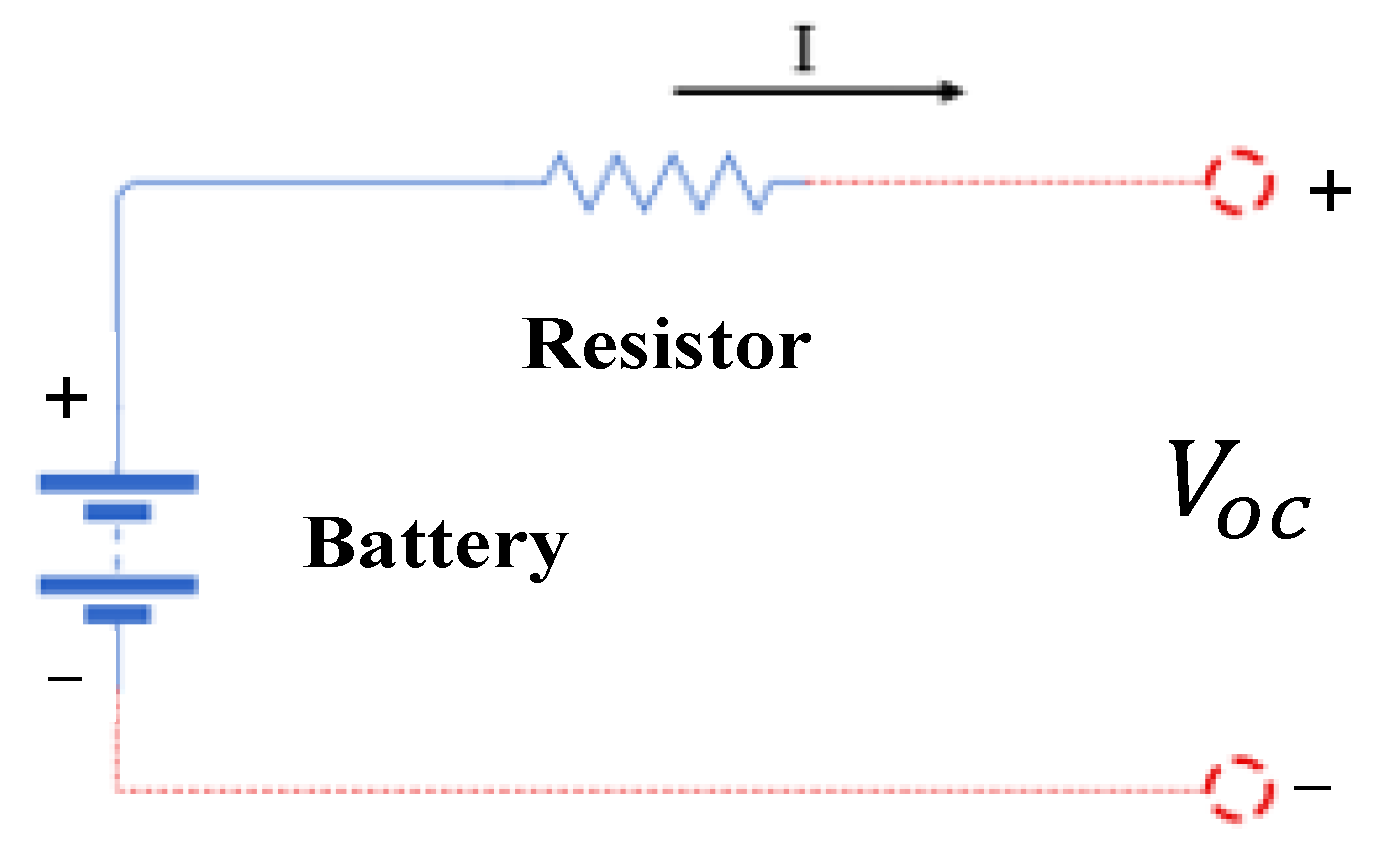
2.2.6. Battery Model
2.2.7. EV Global Model
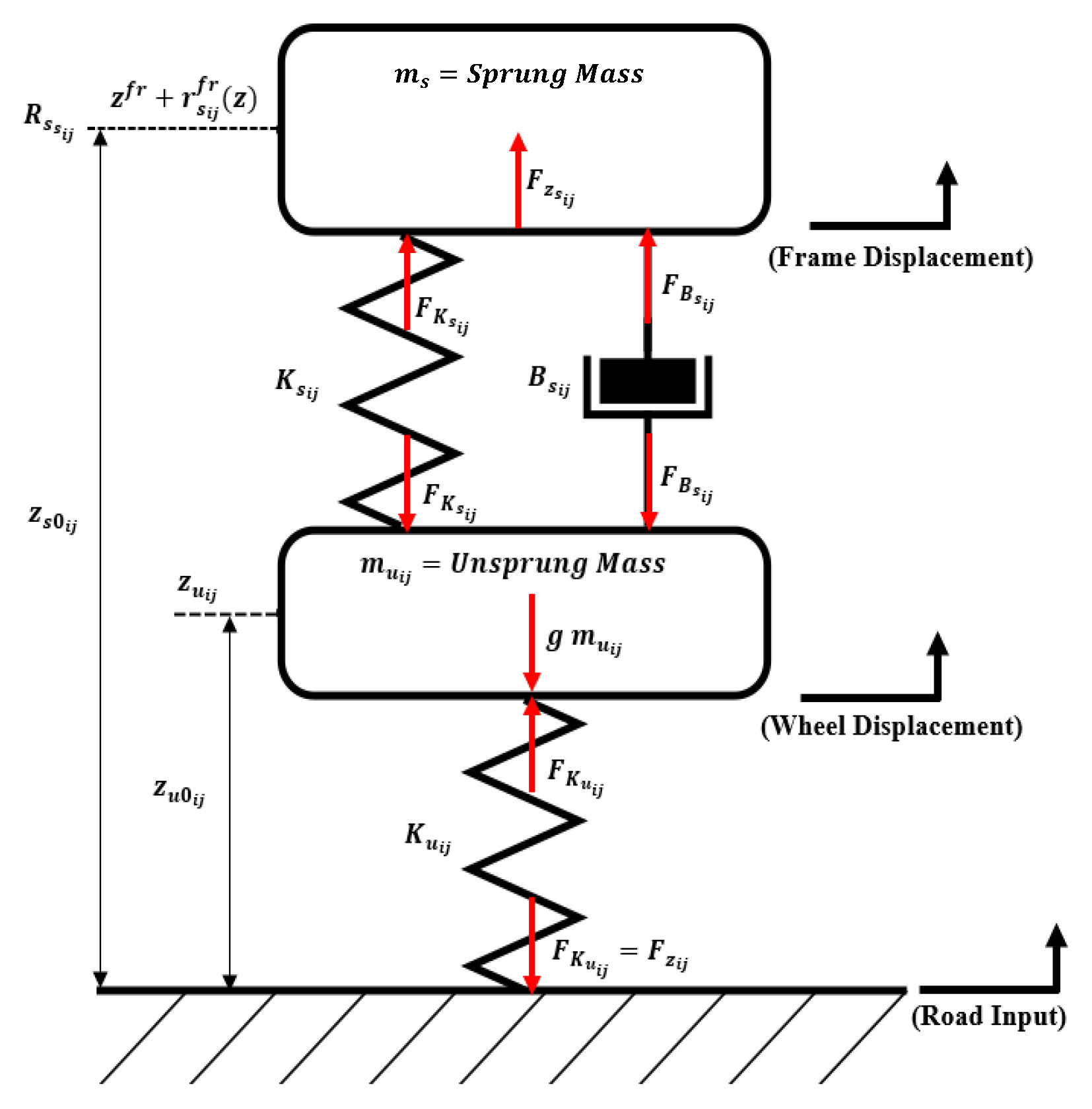
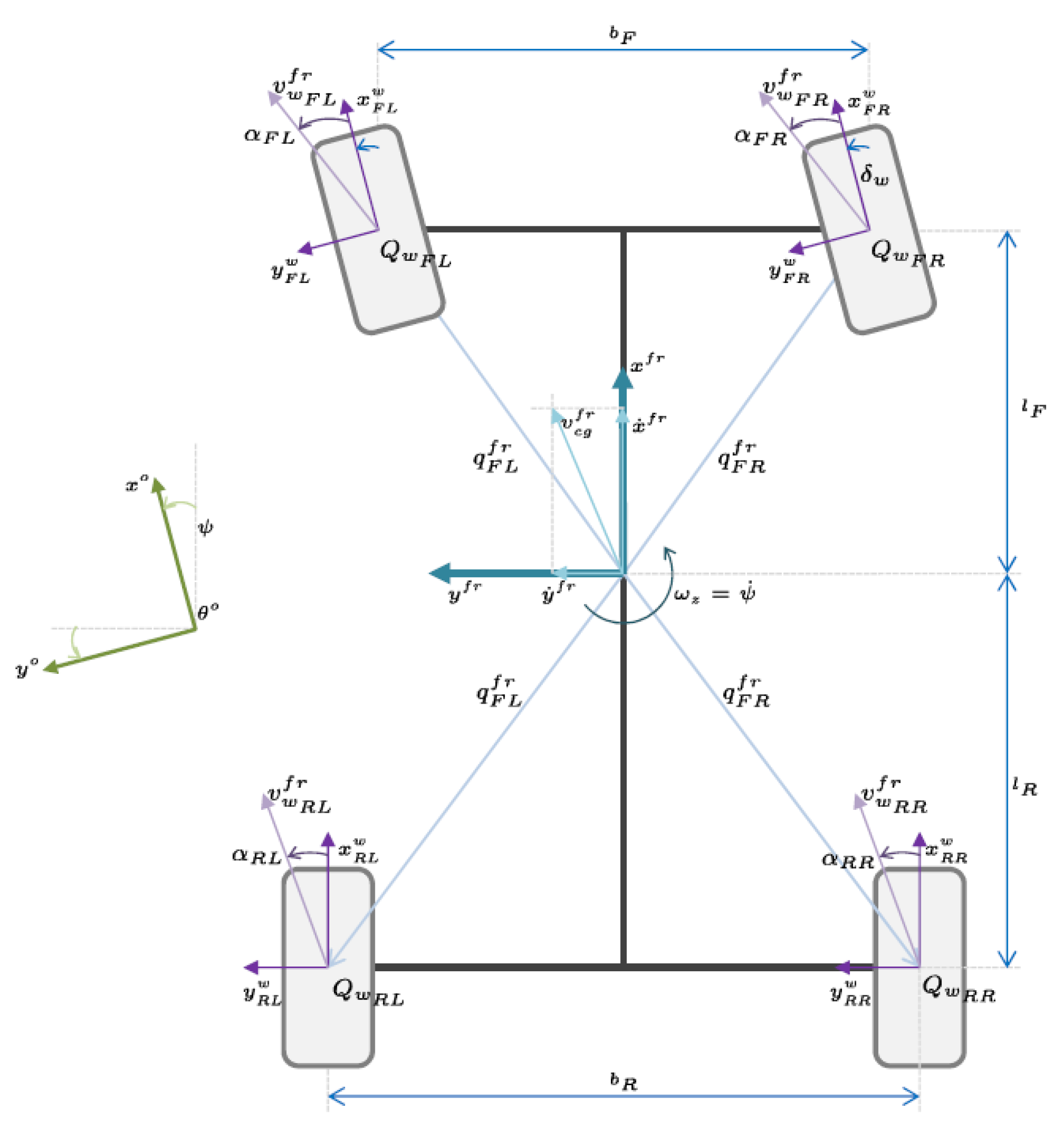
Longitudinal Dynamics
Multibody
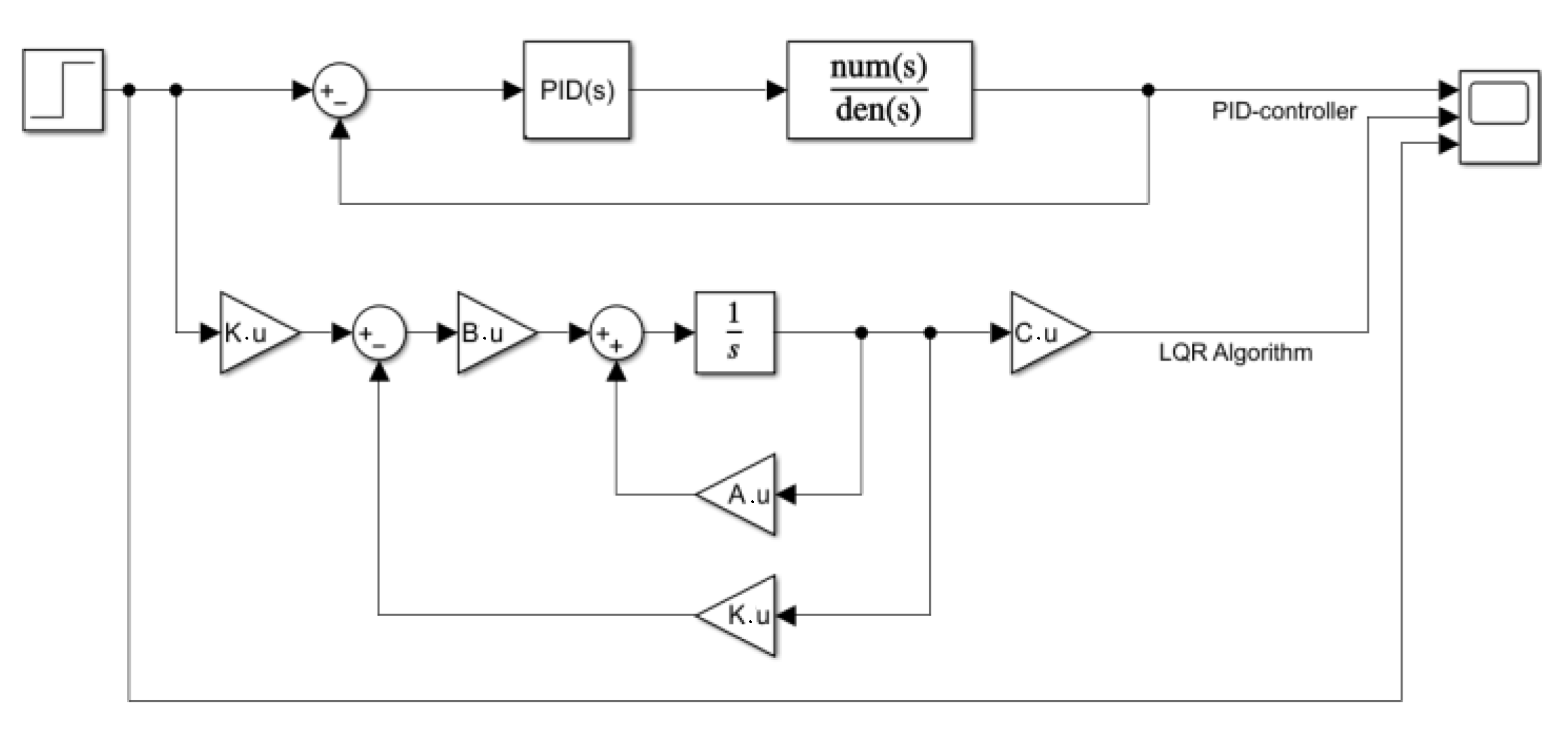
2.3. Simulation
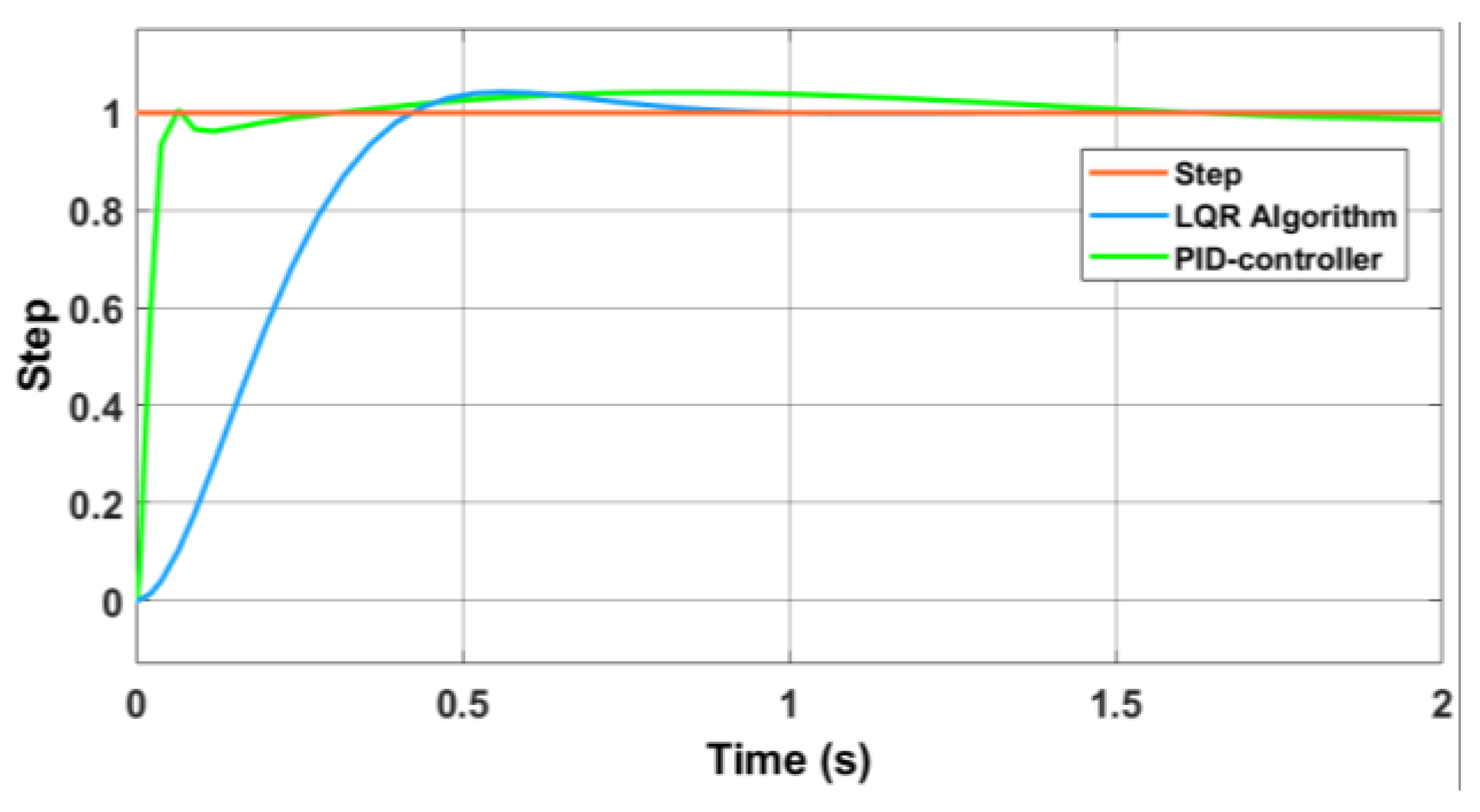
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pettersson, P.; Jacobson, B.; Bruzelius, F.; Johannesson, P.; Fast, L. Intrinsic differences between backward and forward vehicle simulation models. IFAC PappersOnLine 2020, 53, 14292–14299. [Google Scholar] [CrossRef]
- Ibrahim, A.; Jiang, F. The electric vehicle energy management: An overview of the energy system and related modeling and simulation. Renew. Sustain. Energy Rev. 2021, 144, 111049. [Google Scholar] [CrossRef]
- Gao, D.W.; Mi, C.; Emandi, A. Modeling and Simulation of Electric and Hybrid Vehicles. Proc. IEEE 2007, 95, 729–745. [Google Scholar] [CrossRef]
- Li, H.; Xu, P.; Cao, C.; Hu, D.; Yan, X.; Song, Z. Acoustic Simulation of the Electric Vehicle Motor. J. Phys. Conf. Ser. 2021, 2095, 12031. [Google Scholar] [CrossRef]
- Miranda, M.; Silva, F.; Lourenço, M.; Eckert, J.; Silva, L. Electric vehicle powertrain and fuzzy controller optimization using a planar dynamics simulation based on a real-world driving cycle. Energy 2022, 238, 121979. [Google Scholar] [CrossRef]
- Aymen, F.; Alowaidi, M.; Bajaj, M.; Sharma, N.; Mishra, S.; Sharma, S.K. Electric Vehicle Model Based on Multiple Recharge System and a Particular Traction Motor Conception. IEEE Access 2021, 9, 49308–49324. [Google Scholar] [CrossRef]
- Miri, I.; Fotouhi, A.; Ewin, N. Electric vehicle energy consumption modelling and estimation—A case study. Int. J. Energy Res. 2021, 45, 501–520. [Google Scholar] [CrossRef]
- Adegbohun, F.; Von Jouanne, A.; Phillips, B.; Agamloh, E.; Yokochi, A. High Performance Electric Vehicle Powertrain Modeling, Simulation and Validation. Energies 2021, 14, 1493. [Google Scholar] [CrossRef]
- Yaxin, G.; Yi, F. Transmission Parameter Matching and Simulation Verification of Pure Electric Vehicle. J. Phys. Conf. Ser. 2021, 1965, 12015. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Yang, J.; Song, Y. Lateral Stability Control of Four-Wheel-Drive Electric Vehicle Based on Coordinated Control of Torque Distribution and ESP Differential Braking. Actuators 2021, 10, 135. [Google Scholar] [CrossRef]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A user-friendly advanced powertrain simulation using a combined backward/forward approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Kim, N.; Douba, M.; Kim, N.; Rousseau, A. Validation Volt PHEV Model with dynamometer test data using Autonomie. SAE Int. J. Passeng. Cars Mech. Syst. 2013, 6, 985–992. [Google Scholar] [CrossRef]
- Lewis, A.M.; Kelly, J.C.; Keoleian, G.A. Vehicle lightweighting vs. electrification: Life cycle energy and GHC emissions results for diverse powertrain vehicles. Appl. Energy 2014, 126, 13–20. [Google Scholar] [CrossRef]
- Lee, D.; Rousseau, A.; Rask, E. Development and Validation of the Ford Focus Battery Electric vehicle model. SAE Tech. Pap. 2014, 1, 1–9. [Google Scholar] [CrossRef]
- Hou, J.; Guo, X. Modeling and Simulation of hybrid electric vehicles using HEVSIM and ADVISOR. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008. [Google Scholar] [CrossRef]
- Jiang, C.D.; Cheng, L.; Fengchun, S. Study on forward simulation model for extended-range electric bus. In Proceedings of the Third World Congress on Software Engineering, Wuhan, China, 6–8 November 2012. [Google Scholar] [CrossRef]
- He, Y.; Rios, J.; Chowdhury, M.; Pisu, P.; Bhavsar, P. Forward powertrain energy management modeling for assessing benefits of integrating predictive traffic data into plug-in-hybrid electric vehicles. Transp. Res. Part D Transp. Environ. 2012, 17, 201–207. [Google Scholar] [CrossRef]
- Lin, C.; Filipi, Z.; Wang, Y.; Louca, L.; Peng, H.; Assanis, D.; Stein, J. Integrated, Feed-Forward Hybrid Electric Vehicle Simulation in SIMULINK and its Use for Power Management Studies. SAE Tech. Pap. 2002, 1, 1–15. [Google Scholar] [CrossRef]
- Qin, D.; Deng, T.; Yang, Y.; Lin, Z. Regenerative braking simulation research for CVT hybrid electric vehicle with ISG based on forward modeling. Electr. Eng. 2008, 19, 618–624. [Google Scholar]
- Delavaux, M.; Lhomme, W.; Mcgordon, A. Comparison between Forward and Backward approaches for the simulation of an Electric Vehicle. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 3–5 September 2010. [Google Scholar]
- Mohan, G.; Assadian, F.; Longo, S. Comparative analysis of forward-facing models vs. backward-facing models in powertrain component sizing. In Proceedings of the IET Hybrid and Electric Vehicles Conference, London, UK, 6–7 November 2013. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Zhao, X.; Yu, Q.; Ye, Y.; Yu, M. Development of a representative urban driving cycle construction methodology for electric vehicles: A case study in Xi’an. Transp. Res. Part D Transp. Environ. 2020, 81, 102279–102301. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Shamim, T. Performance evaluation of a PEM fuel cell stack with variable inlet flows under simulated driving cycle conditions. Appl. Energy 2017, 206, 751–764. [Google Scholar] [CrossRef]
- Seers, P.; Nachin, G.; Glaus, M. Development of two driving cycles for utility vehicles. Transp. Res. Part D Transp. Environ. 2015, 41, 377–385. [Google Scholar] [CrossRef]
- Yuhui, P.; Yuan, Z.; Huibao, Y. Development of a representative driving cycle of urban buses based on the K-means cluster method. Clust. Comput. 2019, 22, 6871–6880. [Google Scholar] [CrossRef]
- Ye, K.; Li, P.; Li, H. Optimization of hybrid energy storage system control strategy for pure electric vehicle based on typical driving cycle. Math. Probl. Eng. 2020, 2020, 1365195–1365207. [Google Scholar] [CrossRef]
- Kiyakli, A.O.; Solmaz, H. Modeling of an electric vehicle with Matlab/Simulink. Int. J. Automot. Sci. Technol. 2019, 2, 9–15. [Google Scholar] [CrossRef]
- Ali, R.; Furqan, A.; Ho, K.S. Design of fuzzy logic tuned PID controller for electric vehicle based on IPMSM using Fluxweakenning. J. Electr. Eng. Technol. 2018, 13, 451–459. [Google Scholar] [CrossRef]
- Saeed, M.; Ahmed, N.; Hussain, M.; Jafar, A. A comparative study of controllers for optimal speed control of hybrid electric vehicle. In Proceedings of the International Conference on Intelligent Systems Engineering, Islamabad, Pakistan, 15–17 January 2016. [Google Scholar] [CrossRef]
- Heidari, A.; Etedali, S.; Javaheri-Tafti, M. A hybrid LQR-PID control design for seismic control of buildings equipped with ATMD. Front. Struct. Civ. Eng. 2018, 12, 44–57. [Google Scholar] [CrossRef]
- Ma, Z. Parameters design for a parallel hybrid electric bus using regenerative brake model. Adv. Mech. Eng. 2014, 6, 760815–760824. [Google Scholar] [CrossRef]
- Bin Peeie, H.M.; Ogino, H.; Oshinoya, Y. Skid control of a small electric vehicle with two in-wheel motors: Simulation model of ABS and regenerative brake control. Int. J. Crasheorthiness 2016, 21, 396–406. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Ortmann, W.J.; Nefcy, B.; Colvin, D.; Connolly, F. Methods of measuring regenerative braking efficiency in a test cycle. SAE Int. J. Altern. Powertrains 2017, 6, 103–112. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, H.; Zhen, C. Regenerative braking control under sliding braking condition of electric vehicles with switched reluctance motor drive system. Energy 2021, 230, 120901. [Google Scholar] [CrossRef]
- Yilmaz, M. Limitations/capabilities of a electric machine technologies and modeling approaches for electric motor design and analysis in plug-in electric vehicle applications. Renew. Sustain. Energy Rev. 2015, 52, 80–99. [Google Scholar] [CrossRef]
- Park, G.; Lee, S.; Jin, S.; Kwak, S. Integrated modeling and analysis of dynamics for electric vehicle powertrains. Expert Syst. Appl. 2014, 41, 2595–2607. [Google Scholar] [CrossRef]
- Fajri, P.; Lee, S.; Prabhala, V.A.; Ferdowsi, M. Modeling and Integration of electric vehicle regenerative and friction braking for motor/dynamometer test bench emulation. IEEE Trans. Veh. Technol. 2016, 65, 4264–4273. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 100015–110033. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swiercynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef] [Green Version]
- Seaman, A.; Dao, T.S.; McPhee, J. A survey of mathematics based equivalent circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, D.; Deng, L.; Cui, Z.; Lyu, C.; Wang, L.; Pecht, M. Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries. J. Energy Storage 2020, 31, 101538–101551. [Google Scholar] [CrossRef]
- Choi, W.; Shin, H.C.; Kim, H.C.; Choi, J.Y.; Yoon, W.S. Modeling and applications of electrochemical impedance spectroscopy (Eis) for lithium-ion batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Abdollahi, A.; Han, X.; Raghunathan, N.; Pattipati, B.; Balasingam, B.; Pattipati, K.R.; Bar-Shalom, Y.; Card, B. Optimal charging for general equivalent electrical battery model and battery life management. J. Energy Storage 2017, 9, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Da Lio, M.; Bortoluzzi, D.; Pietro Rosati Papini, G. Modeling longitudinal vehicle dynamics with neural networks. Veh. Syst. Dyn. 2020, 58, 1675–1693. [Google Scholar] [CrossRef] [Green Version]
- Esmailzadeh, E.; Vossoughi, C.R.; Goodarzi, A. Dynamic modeling and analysis of a four motorized wheels electric vehicle. Veh. Syst. Dyn. 2001, 35, 163–194. [Google Scholar] [CrossRef]
- Juhala, M. Improving vehicle rolling resistance and aerodynamics. In Alternative Fuels and Advances Vehicle Technologies for Improved Environmental Performance; Folkson, R., Ed.; Woodhead Publishing: Cambridge, UK, 2014; pp. 462–475. [Google Scholar]
- Hegazy, S.; Rahnejat, H.; Hussain, K. Multi-body dynamics in full vehicle handling analysis. Proc. Inst. Mech. Eng. Part K. J. Multi-Body Dyn. 1999, 213, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Blundell, M.; Harty, D. The Multibody System Approach to Vehicle Dynamics, 2nd ed.; Elsevier Butterworth Heinemann: New York, NY, USA, 2004; Volume 1, pp. 30–160. [Google Scholar]
- Lo, R.; Massaro, M.A. Symbolic approach to the multibody modeling of road vehicles. Int. J. Appl. Mech. 2017, 9, 17500685. [Google Scholar] [CrossRef]
- Milliken, M.F.; Milliken, D.L. Race Car Vehicle Dynamic, 2nd ed.; Society of Automotive Engineers: Warrendale, PA, USA, 1994. [Google Scholar]
- Wang, J.; Qiao, J.; Qi, Z. Research on control strategy of regenerative braking and anti-lock braking system for electric vehicle. In Proceedings of the World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 1–7 November 2013. [Google Scholar] [CrossRef]
- Yu, C.; Shim, T. Modeling of comprehensive electric drive system for a study of regenerative brake system. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar] [CrossRef]
- Moreno, P.; Blanco, M.; Lafoz, M.; Arribas, J.R. Educational Project for the teaching of control of electric traction drives. Energies 2015, 8, 921–938. [Google Scholar] [CrossRef] [Green Version]
- Rahimirad, P.; Masih-Tehrani, M.; Dahmardeh, M. Battery life investigation of a hybrid energy management system considering battery temperature effect. Int. J. Automot. Eng. 2019, 9, 2966–2976. [Google Scholar]


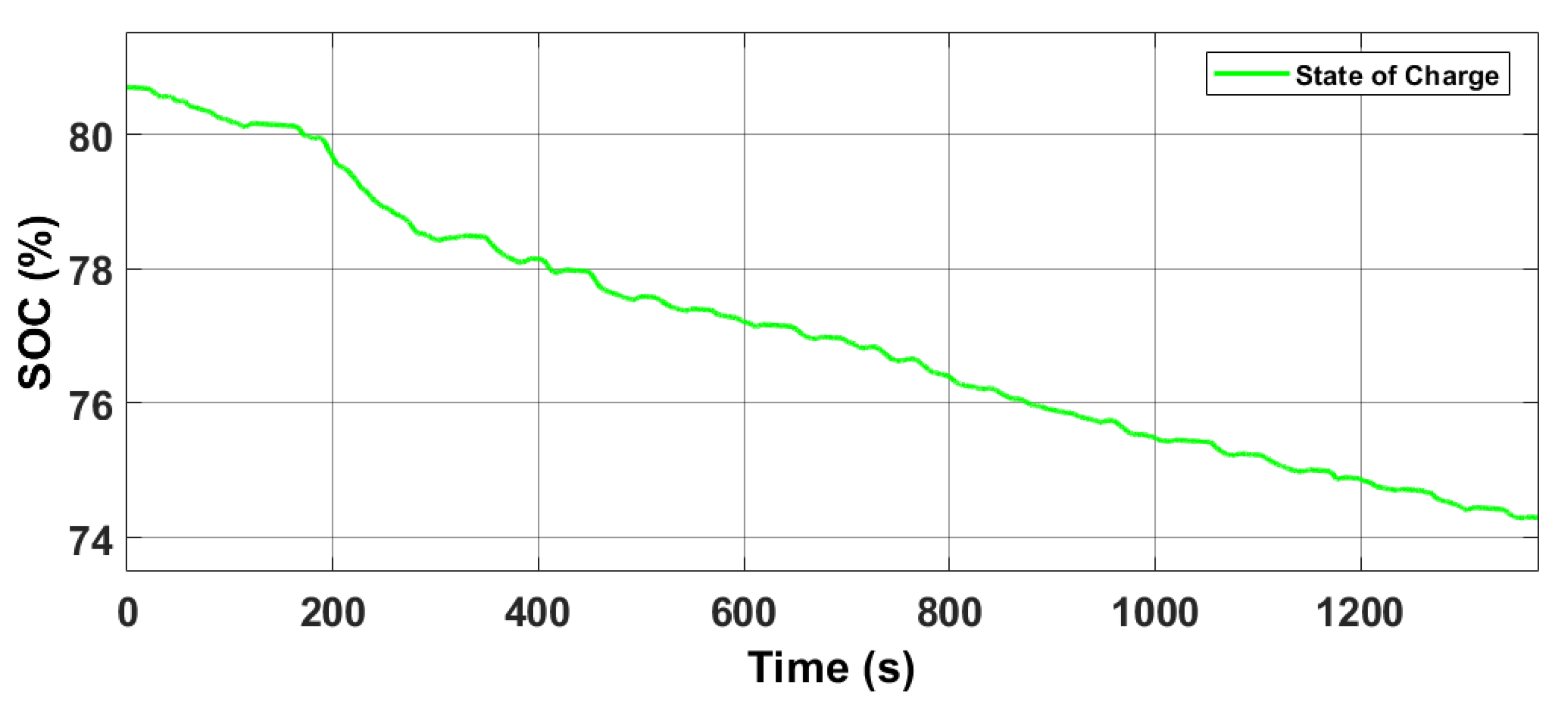
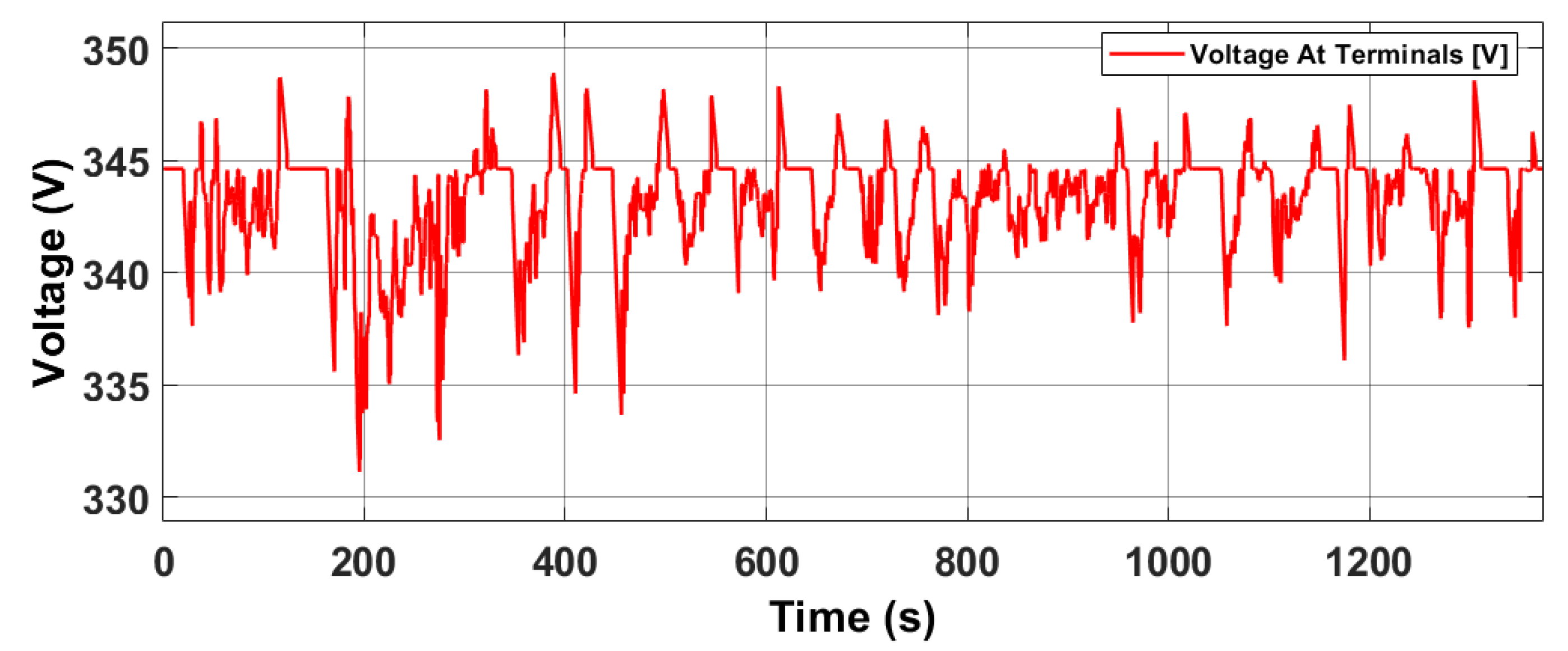
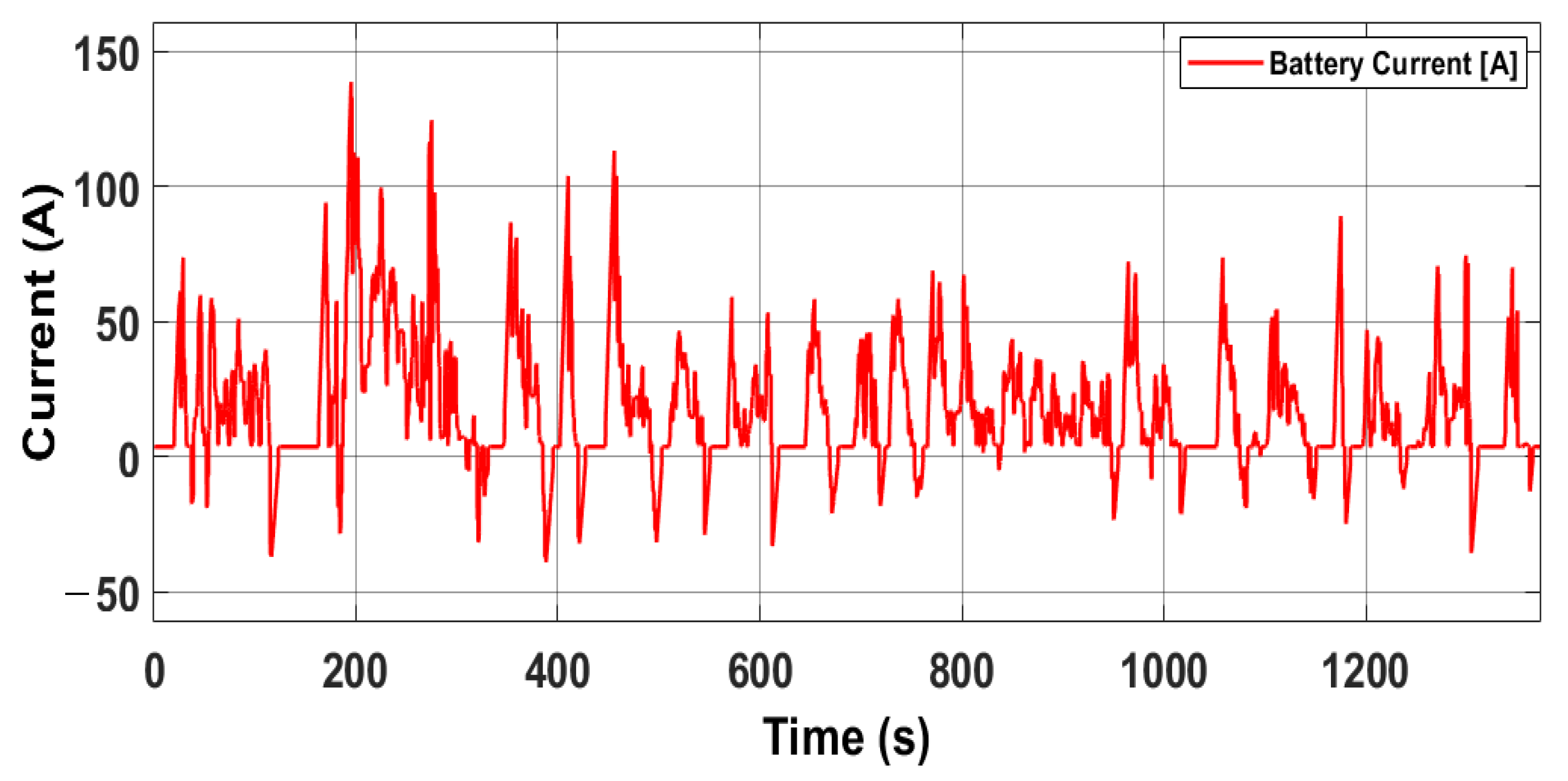
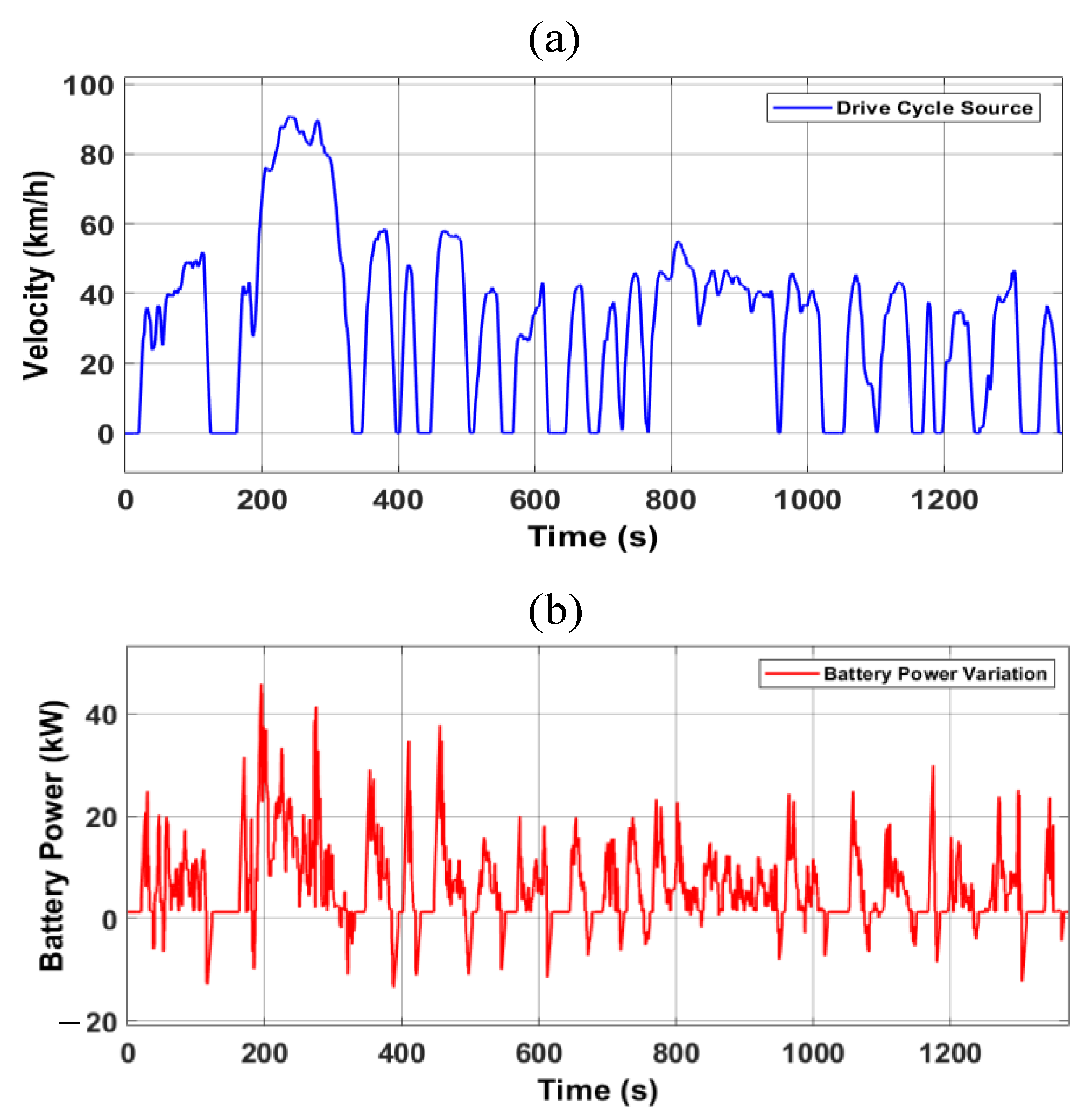
| Description | Parameter | Value | Unit |
|---|---|---|---|
| Vehicle mass | 1700 | kg | |
| Vehicle front area | 2.42 | ||
| Wheel radius | 0.321 | ||
| Transmission ratio | 7.82:1 | - | |
| Drag coefficient | 0.26 | - | |
| Rolling resistance coefficient | 0.013 | - | |
| Maximum torque electric motor | 250 | Nm | |
| Maximum power electric motor | 107 | kW | |
| Motor torque loss constant | 0.12 | ||
| Motor work loss constant | 0.01 | J | |
| Motor inertia loss constant | 1.2 × 10−5 | ||
| Battery capacity | 23 | kWh | |
| Voltage | 350 | V | |
| Internal resistance | 0.1 | Ohm | |
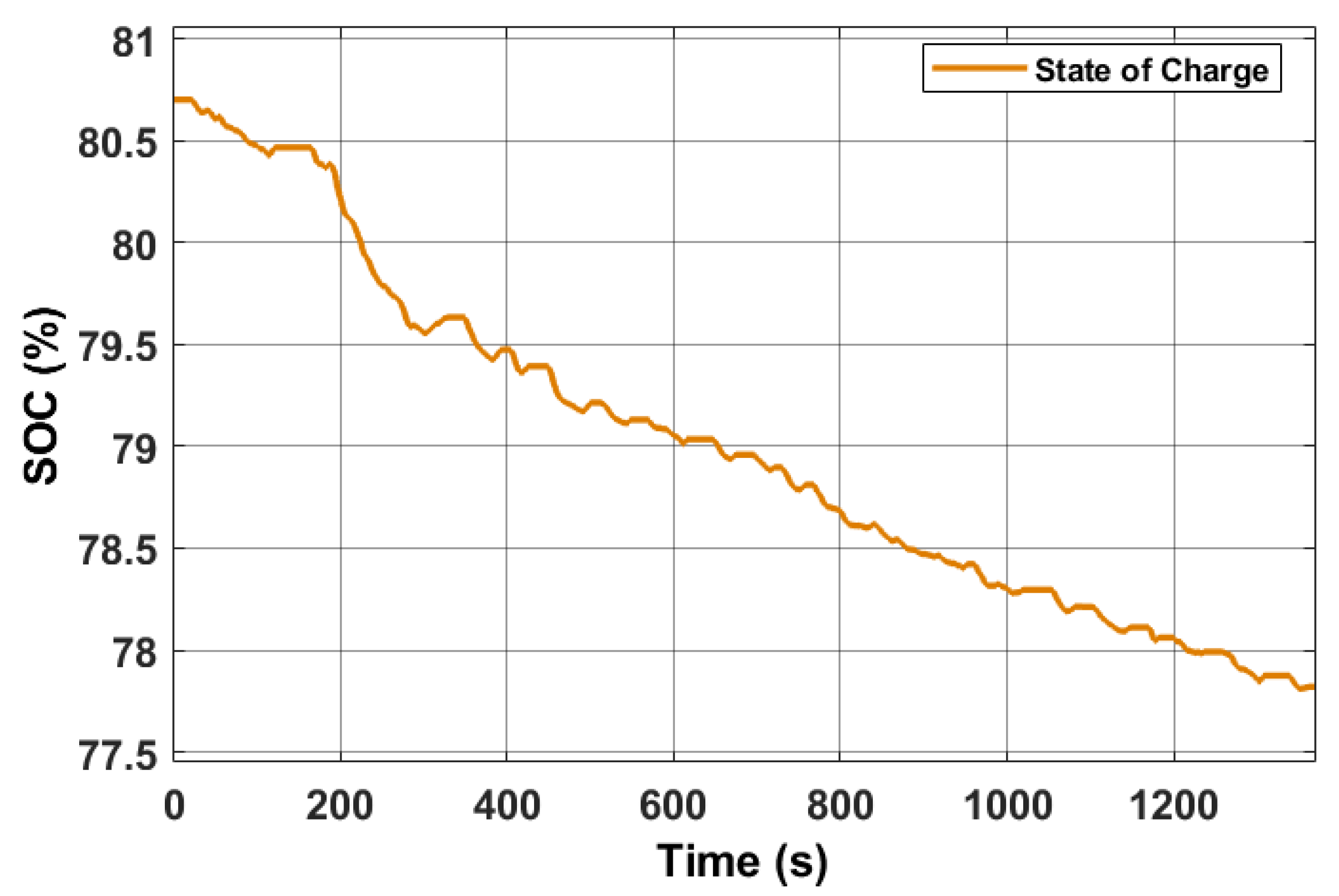
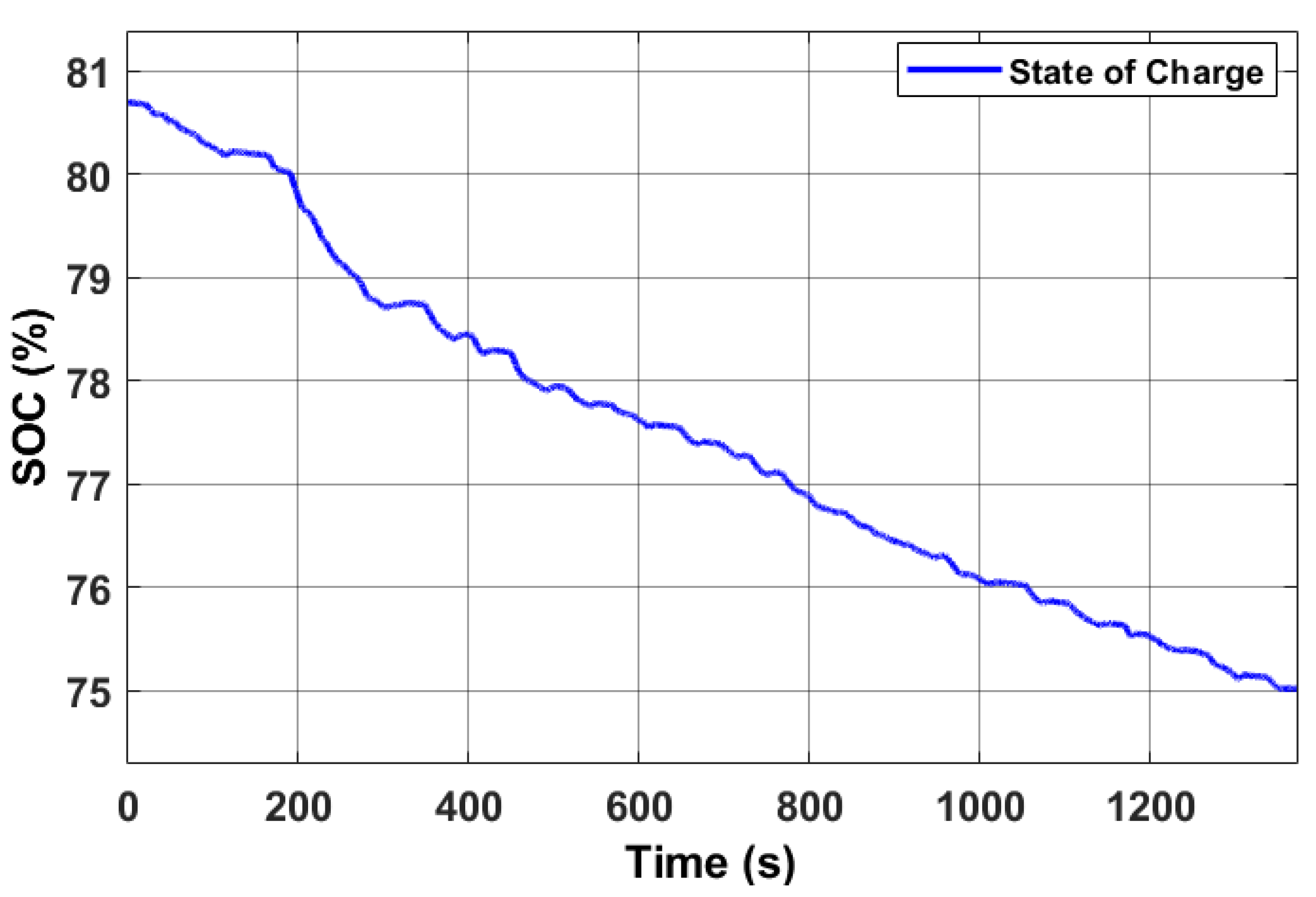
| SOC initial | 80.7 | % |
| Parameter | UDDS Cycle |
|---|---|
| Distance | 11.99 km |
| SOC at the end of the cycle | 74.3% |
| Energy consumed | 2209 kWh |
| Power loss in the electric motor | 0.429 kWh |
| Transmission power loss | 0.221 kWh |
| Battery power loss | 0.0324 kWh |
| Parameter | Developed Model | Matlab Model | Ref. [14] |
|---|---|---|---|
| Distance | 11.99 km | 11.98 km | 11.99 km |
| SOC at the end of the cycle | 74.3% | 77.97% | 75% |
| Energy consumed | 2209 kWh | 2078 kWh | 2145 kWh |
| Autonomy | 4.45 kWh/100 km | 1.22 kWh/100 km | 0.97 kWh/100 km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montaleza, C.; Arévalo, P.; Tostado-Véliz, M.; Jurado, F. Intrinsic Characteristics of Forward Simulation Modeling Electric Vehicle for Energy Analysis. Electricity 2022, 3, 202-219. https://doi.org/10.3390/electricity3020012
Montaleza C, Arévalo P, Tostado-Véliz M, Jurado F. Intrinsic Characteristics of Forward Simulation Modeling Electric Vehicle for Energy Analysis. Electricity. 2022; 3(2):202-219. https://doi.org/10.3390/electricity3020012
Chicago/Turabian StyleMontaleza, Christian, Paul Arévalo, Marcos Tostado-Véliz, and Francisco Jurado. 2022. "Intrinsic Characteristics of Forward Simulation Modeling Electric Vehicle for Energy Analysis" Electricity 3, no. 2: 202-219. https://doi.org/10.3390/electricity3020012
APA StyleMontaleza, C., Arévalo, P., Tostado-Véliz, M., & Jurado, F. (2022). Intrinsic Characteristics of Forward Simulation Modeling Electric Vehicle for Energy Analysis. Electricity, 3(2), 202-219. https://doi.org/10.3390/electricity3020012









