Effects of Exceptional Points on the Optical Properties of a Quantum Dot in a Microcavity ^†

Abstract

We theoretically study the effect of quantum exceptional points on the optical properties of a quantum dot placed inside an optical microcavity and interacting with a weak probe field. Using a quantum approach, we study the steady-state behavior of the system and calculate the optical susceptibility. By separating the total susceptibility into two equivalent susceptibilities, corresponding to fictitious free quantum emitters, we show exceptional points’ drastic effect on the optical properties of the system close to the region where the exceptional point is formed. We further examine the optical properties of the system in the regions of the parameter space that arise from the exceptional condition, namely the strong coupling regime and the weak coupling regime.

1. Introduction

Exceptional points (EPs) have been studied in a plethora of classical optical systems [1,2,3,4] and can dramatically modify the optical response of a studied system. Recently, there is increasing interest in applying the EP formalism in fully quantum systems to achieve efficient control at the quantum level and to show the drastic effect that EPs have on a system’s properties [5,6,7,8]. In this work, we theoretically study the effect of quantum EPs on the optical properties of a quantum dot placed inside an optical microcavity and interacting with a weak probe field. For the analysis of the system, we use a quantum approach, where we model the quantum dot as a two-level system and describe the light–matter interaction with the proper master equation, including the spontaneous decay and the pure dephasing of the quantum dot, as well as the decay of the optical cavity. We also define the effective non-Hermitian Hamiltonian of the system and derive the necessary conditions for the formation of an EP, the point where the eigenvalues of the Hamiltonian coalesce.

We then study the steady-state behavior of the system and calculate the optical susceptibility from the coherence between the vacuum and the system, which can lead to cavity-induced transparency [9,10]. By separating the total susceptibility into two equivalent susceptibilities, corresponding to fictitious free quantum emitters, we show EPs’ drastic effect on the optical properties of the system close to the region where the exceptional point is formed. We further examine the optical properties of the system in the regions of the parameter space that arise from the exceptional condition, namely the strong (coherent) coupling regime and the weak (incoherent) coupling regime. In conclusion, we give an overview of the effect of EPs in a purely quantum system and we show how they affect its classical properties.

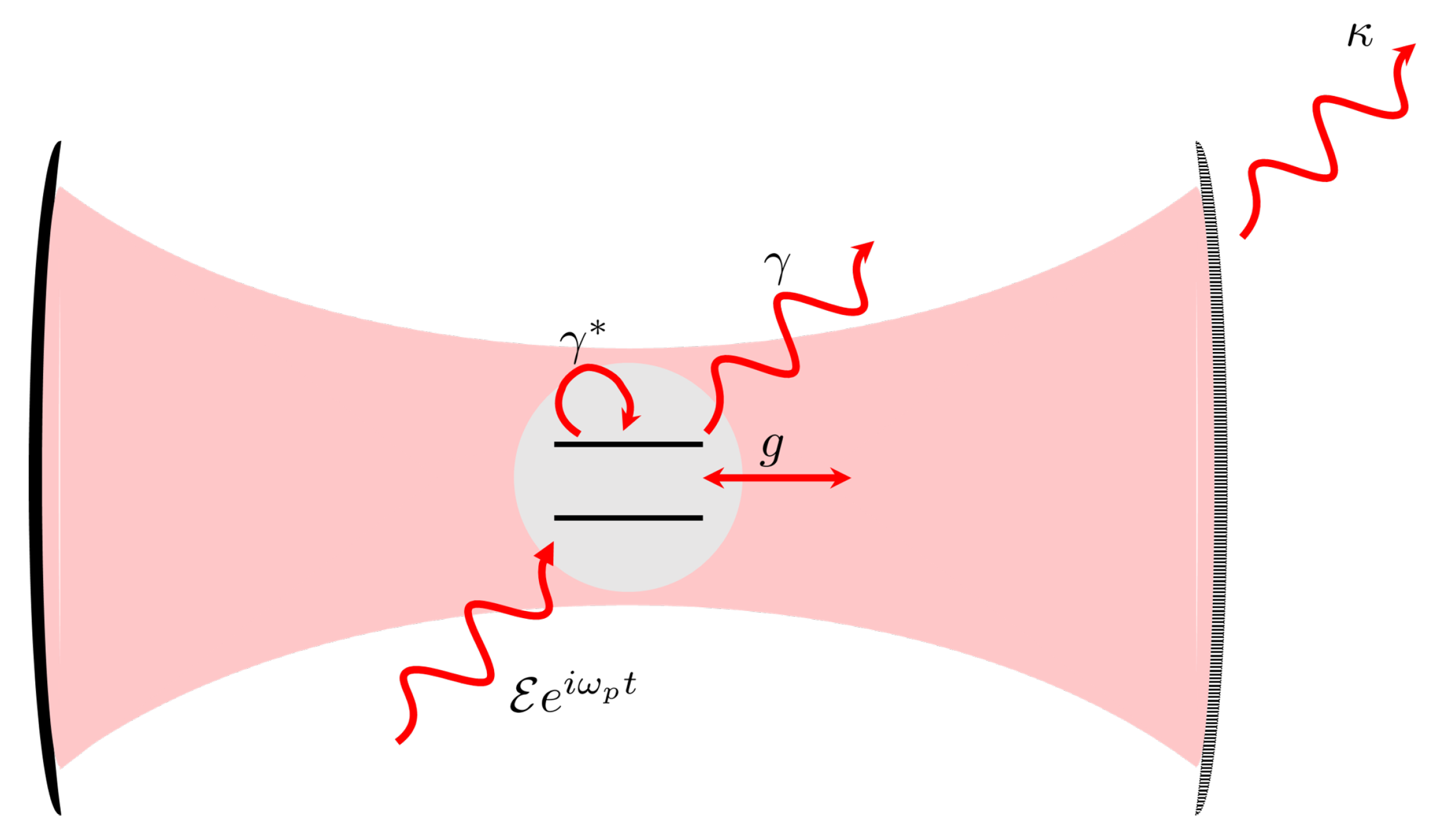
2. Materials and Methods

We consider a system consisting of a quantum dot, modeled as a two-level quantum emitter (QE), placed inside an optical microcavity, as illustrated in Figure 1. The QE is coupled to the electromagnetic field inside the cavity with coupling rate g. The QE is also subject to decay $\gamma$ due to spontaneous emission and a pure dephasing rate ${\gamma }^{*}$ (in our analysis, we take ${\gamma }^{*}={10}^4\gamma$ to be in agreement with solid-state QEs such as quantum dots). Additionally, the cavity decays in free space at a decay rate of $\kappa$. Lastly, we consider an external probe electromagnetic field, $E=\mathcal{E}{e}^{i{\omega }_{p}t}+c.c.$, that interacts with the QE. Thus, the Hamiltonian is $H_0={\omega }_a{\sigma }^{+}{\sigma }^{-}+{\omega }_c{a}^{†}a+g{\sigma }^{+}a+\Omega e^{i\Delta t}{\sigma }^{+}+h.c.$, where $\Omega =\mu \mathcal{E}$ corresponds to the Rabi frequency of the $e\to g$ transition, $\mu$ is the dipole moment of the QE, and $\Delta ={\omega }_p-{\omega }_a$ is the detuning. In this work, we take $\hslash =1$. We can define an effective non-Hermitian Hamiltonian that encompasses both the coherent and the dissipative terms of our system, given by $H_{eff}=H_0-(i\kappa /2)a^{†}a-(i\gamma /2){\sigma }^{+}{\sigma }^{-}-(i{\gamma }^{*}/2){\sigma }_z^{†}{\sigma }_z$.

We investigate the eigenvalues of the effective Hamiltonian for the case of a weak probe field, meaning $\Omega \ll g,\gamma ,\kappa$. The point where the eigenvalues coalesce corresponds to the condition $2g/|\gamma +{\gamma }^{*}-\kappa |=1/2$, which is independent of the probe field. In order to study the optical properties of the system, we need to study its dynamics and steady state by solving the Lindblad equation and evaluating its coherence with the vacuum. We find that the susceptibility is given by

$$\chi =\xi \frac{\Delta +i\frac{\kappa }{2}}{g^2-\left(\Delta +i\frac{\gamma +{\gamma }^{*}}{2}\right)\left(\Delta +i\frac{\kappa }{2}\right)}.$$

(1)

where $\xi =N\mu /{\epsilon }_0$, in which N is the atomic density of the quantum dot and ${\epsilon }_0$ is the vacuum permittivity. The imaginary part of the susceptibility is a measure of the probe absorption of the system, and the real part shows the dispersion relation of the system.

We separate the total susceptibility of the system into two parts, corresponding to two “free QE” susceptibilities, such that $\chi ={\chi }_1+{\chi }_2$, which are given by

$$\begin{array}{cc}\hfill {\chi }_1& =\xi \left(\frac{i(\gamma +{\gamma }^{*}-\kappa )}{2\sqrt{Z}}-1\right)\left(\frac{1}{2\Delta -\sqrt{Z}+i(\gamma +{\gamma }^{*}-\kappa )/2}\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\chi }_2& =\xi \left(\frac{i(\kappa -\gamma -{\gamma }^{*})}{2\sqrt{Z}}-1\right)\left(\frac{1}{2\Delta +\sqrt{Z}+i(\gamma +{\gamma }^{*}-\kappa )/2}\right),\hfill \end{array}$$

(3)

where $Z=4g^2-{(\gamma +{\gamma }^{*}-\kappa )}^2/4$. These “free QE” susceptibilities are of the form $\chi =\xi \frac{A}{(\Delta -{\Delta }_0)+iw/2}$, of which the real and imaginary parts are the well-known dispersion ${\chi }^r=\xi \frac{A(\Delta -{\Delta }_0)}{{(\Delta -{\Delta }_0)}^2+{(w/2)}^2}$ and Lorentzian absorption ${\chi }^i=\xi \frac{A(w/2)}{{(\Delta -{\Delta }_0)}^2+{(w/2)}^2}$ curves, respectively, with amplitude A which is a complex number.

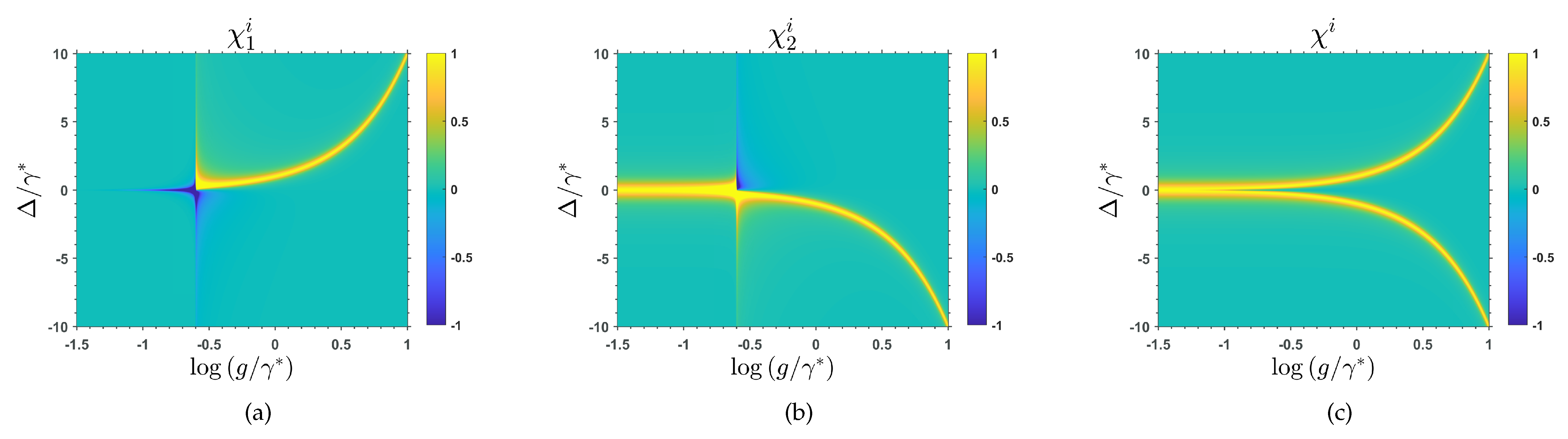
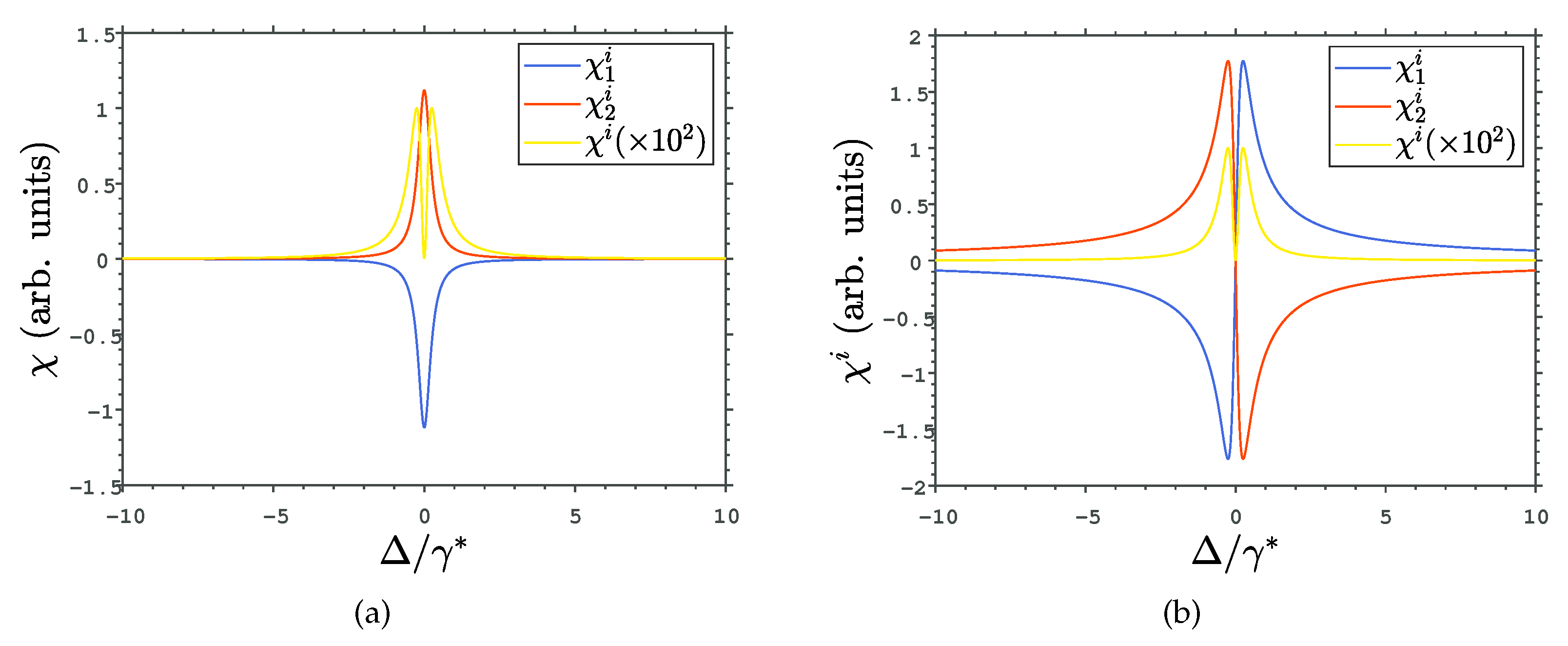
3. Results and Discussion

In Figure 2, we plot the imaginary part of the susceptibilities corresponding to the absorption of each “free QE” and of the total system for weak cavity decay $\kappa =0.001\gamma$ and strong dephasing rate ${\gamma }^{*}={10}^4\gamma$ as a function of the coupling g and the detuning $\Delta$. We clearly see that for $2g/|\gamma +{\gamma }^{*}-\kappa |=1/2$, the “free QE” susceptibilities tend toward infinity while the system’s susceptibility is finite and has two well-separated, symmetric peaks. Thus, we can split the parameter space into two regions: the region of incoherent coupling $2g/|\gamma +{\gamma }^{*}-\kappa |<1/2$ and the region of strong coupling $2g/|\gamma +{\gamma }^{*}-\kappa |>1/2$. Special treatment is given to the region where $2g/|\gamma +{\gamma }^{*}-\kappa |\to 1/2$. In the incoherent coupling region, ${\chi }_1^i$ is a narrow Lorentzian curve centered around $\Delta =0$ with negative amplitude, while ${\chi }_2^i$ is a wide Lorentzian curve centered around $\Delta =0$ with positive amplitude. As g decreases, ${\chi }_1^i$ becomes narrower and with smaller amplitude while ${\chi }_2^i$ practically stays the same; thus, the “dip” of the total susceptibility ${\chi }^i$ at zero detuning becomes less visible. In the coherent coupling regime, ${\chi }_1^i$ and ${\chi }_2^i$ are well separated and symmetric around zero detuning, making the total susceptibility ${\chi }^i$ have two distinct symmetric brunches. More specifically, for a large enough coupling, only the Lorentzian part contributes; thus, each curve has at their center the detuning $\Delta =\pm \sqrt{Z}/2$ and width $w=(\gamma +{\gamma }^{*}+\kappa )/2$. While the width stays the same as the coupling increases, their amplitude decreases at approximately $1/g$.

Lastly, we investigated the behavior of the susceptibilities close to the EP as a function of the detuning (see Figure 3). We observe that the closer the EP, the larger the “free-QE” susceptibilities, and thus, exactly at the EP, they diverge to infinity. Additionally, the way the “free-QE” susceptibilities diverge depends on the sign of the detuning and on the region from which we approach the EP (depends on the type of limit, $2g/|\gamma +{\gamma }^{*}-\kappa |\to 1/2^{\pm }$). When the system approaches the EP from the incoherent coupling region, the two susceptibilities correspond to a Lorentzian function (Figure 3), which are centered at zero detuning and have comparable and opposite amplitudes. At the limit, ${\chi }_1^i$ diverges to $-\infty$ and ${\chi }_2^i$ diverges to $+\infty$ for all $\Delta$, but the total susceptibility remains a positive finite number. Thus, the total susceptibility has a wide “dip” at zero detuning and two symmetric peaks. When the system approaches the EP from the coherent coupling region, both susceptibilities correspond to Lorentzian dispersion functions (Figure 3). Similar to the previous case, at the limit, ${\chi }_1^i$ diverges to $+\infty$ for negative detuning and to $-\infty$ for positive detuning, while ${\chi }_2^i$ diverges to $-\infty$ for negative detuning and to $+\infty$ for positive detuning. Again, the total susceptibility is finite, and we see that it is a continuous function (${lim}_{g\to g_{EP}^{\pm }}\chi =\chi$).