Strong Light–Matter Interaction of a Quantum Emitter near a Graphene Nanodisk ^†

Abstract

We study the spontaneous emission dynamics of a quantum emitter near a graphene nanodisk. We analyze the population dynamics of the excited state of the quantum emitter and also explore its dynamics as a non-Markovian open system. Specifically, we quantify the non-Markovian spontaneous emission dynamics using different non-Markovianity measures and calculate the quantum speed limit under non-Markovian evolution. We find strong light-matter coupling conditions for the quantum emitter near the graphene nanodisk, which are manifested in either distinct decaying Rabi oscillations or population trapping effects in the excited state population dynamics of the quantum emitter, depending on the parameters of the system. We also show that the values of the non-Markovianity measures and of the potential quantum speed up are large under strong light–matter coupling conditions.

1. Introduction

The strong coupling between quantum emitters (QEs) and the modified electromagnetic field by plasmonic nanostructures has attracted significant interest in recent years due to numerous potential applications in various areas of technology [1]. In the time regime, the strong light–matter coupling appears as reversible, non-Markovian, spontaneous emission (SE) dynamics in the QE. Besides traditional plasmonic nanostructures made of noble metals, graphene has also emerged as an alternative to metallic nanostructures in nanophotonics [2,3]. Graphene supports surface plasmon modes that lie in the infrared regime [4] and are controllable by different processes including electric field gating and doping. The interaction of QEs with light near graphene nanostructures, like the graphene nanodisk, is a topic of active research [4,5,6,7]. The important work of Koppens, Chang, and Abajo [4] showed that a graphene nanodisk is an ideal platform for strong light–matter coupling and it can be used in quantum optics at single photon level when a QE is placed near the graphene nanodisk. Interestingly, the SE dynamics of a QE near a graphene nanodisk have never been analyzed. This is the purpose of the present work.

Here, we study the dynamics of the SE of a QE placed near a graphene nanodisk with application of the macroscopic quantum electrodynamics approach [8]. This approach combines electromagnetic calculations, for the calculation of the Purcell factor for the QE near the graphene nanodisk, and quantum dynamics calculations, using the probability amplitude approach without applying the Markov approximation, which incorporate the Purcell factor. Our work also goes beyond the calculation of the population dynamics of the excited state of the QE, and we also analyze the non-Markovian SE dynamics using widely-accepted non-Markovianity measures [9,10]. In addition, we calculate the quantum speed limit [11] for the evolution of the QE near the graphene nanodisk.

2. Theory

We investigate the SE dynamics of a QE interacting with a single photon near a graphene nanodisk, as shown on the left side in Figure 1. In the coordinate system we use, the $xy$-plane coincides with the nanodisk and the z-axis is perpendicular to the nanodisk. Also, the origin of the coordinate system is taken at the center of the nanodisk. The QE is placed in vacuum at distance d from the center of the nanodisk.

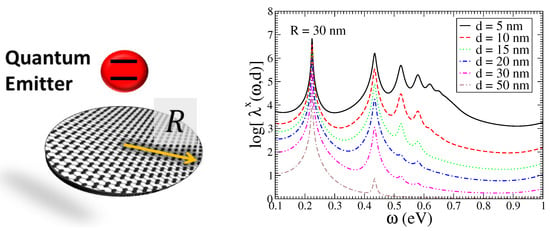
Figure 1. (color online) Left: Schematic representation of a two-level QE placed above a graphene nanodisk of radius R. Right: The Purcell enhancement factor for a QE with transition dipole moment along the x-axis at various distances from a graphene nanodisk with radius $R=30$ nm.

The methodology of calculation has been described in previous work on other nanostructures (see, for example, Refs. [12,13]). The directional Purcell factor is crucial for quantifying the influence of the photonic environment created by the nanodisk on the QE’s SE process; it is defined as:

$${\lambda }^x(\omega ,\mathbf{r})=\frac{{\mathsf{\Gamma }}^x(\omega ,\mathbf{r})}{{\mathsf{\Gamma }}_0\left(\omega \right)}=1+\frac{6\pi c}{\omega }{\widehat{n}}_x·\mathrm{Im}\widehat{\mathbf{G}}(\mathbf{r},\mathbf{r},\omega )·{\widehat{n}}_x,$$

(1)

where ${\mathsf{\Gamma }}^x(\omega ,\mathbf{r})$ is the x-directional relaxation rate of a QE, placed in vacuum, in proximity to the nanodisk, and $\widehat{\mathbf{G}}$ is the induced part of the electromagnetic Green’s tensor, due to the nanodisk, calculated at the QE position, which represents the response of the graphene nanodisk under consideration of a point-like dipole excitation [8]. Also, ${\widehat{n}}_x$ is the unit vector along the x direction of the transition dipole moment. Details on the calculation of the electromagnetic Green’s tensor and the corresponding Purcell factor are given in Ref. [5]. The Purcell factors for a QE with x-oriented transition dipole moment located at various distances d are presented on the right side in Figure 1. Various narrow peaks are observed and strong enhancement of the Purcell factor is shown. These are clear indications that strong light–matter interaction is possible for a QE near the graphene nanodisk.

3. Results and Discussion

For simplicity we take $\hslash =1$. In the top panel of Figure 2, we present the SE dynamics of a QE with transition frequency ${\omega }_0=0.22379$ eV (the first peak of the Purcell factor) and x-oriented transition dipole moment at distance $d=5$ nm from the nanodisk. The QE takes different free-space decay rates ${\mathsf{\Gamma }}_0$ between 0.0008 $\mathsf{\mu }$eV and 41.36 $\mathsf{\mu }$eV. In the inset of this panel, we present the SE dynamics for the largest ${\mathsf{\Gamma }}_0$, which implies the strongest light–matter interaction strength between the QE and the electromagnetic mode continuum modified by the graphene nanodisk, as the coupling strength is proportional to the free-space decay rate ${\mathsf{\Gamma }}_0$. As it can be seen, the excited state population at early times rapidly oscillates with decay and gradually attains a steady non-zero value, about 30% of the initial population. So, partial population trapping in the QE occurs, which can be attributed to the formation of a stationary superposition state between the QE and the electromagnetic mode continuum occurring due the very strong coupling between them [14].

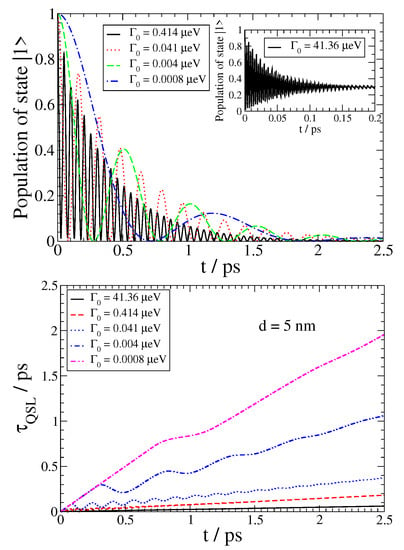
Figure 2. (color online) Top: SE dynamics for different ${\mathsf{\Gamma }}_0$ values for a QE with ${\omega }_0=0.22379$ eV and x-oriented transition dipole moment located at $d=5$ nm. Bottom: Quantum speed limit ${\tau }_{QSL}$ for the SE dynamics of a QE with ${\omega }_0=0.22379$ eV with x-oriented dipole moment located at $d=5$ nm.

In the main part of the top panel of Figure 2, we present the excited state decay dynamics for smaller free-space decay rates. In these cases, no partial population trapping is observed. However, clear decaying Rabi oscillations are found, where the excited state population oscillates in total back and forth between the electromagnetic mode continuum and the QE, while overall it gradually decays completely within about 2 to 2.5 ps. Thus, we conclude that the observed population dynamics indicates that the SE evolution in all such cases is clearly non-Markovian.

We also investigate the non-Markovian behavior of the SE dynamics in the presence of a graphene nanodisk of radius $R=30$ nm by using the non-Markovianity BLP measure $\mathcal{N}$ and the two RHP measures ${\mathcal{I}}^{\left(E\right)}$ and $\mathcal{I}$ [10]. In Table 1, we present the values for the above measures for a QE located at $d=5$ nm from a graphene nanodisk of radius $R=30$ nm. Apparently, the more the underlying population dynamics of the QE is non-Markovian, as shown in the top panel in Figure 2, the larger are the calculated non-Markovianity measure values, when no population trapping occurs.

Table 1. Non-Markovianity measure values [9,10] for various ${\mathsf{\Gamma }}_0$ of a QE with a x-oriented transition dipole moment located at $d=5$ nm from a graphene nanodisk of radius $R=30$ nm.

	$\mathit{d}=5$ nm
${\mathsf{\Gamma }}_{\mathbf{0}}$/$\mathsf{\mu }$eV	41.36	0.414	0.041	0.004	0.0008
$\mathcal{N}$	14.2	12.44	5.45	1.51	0.43
${\mathcal{I}}^{\left(E\right)}$	26.12	24.89	10.89	3.02	0.86
$\mathcal{I}$	51.63	272.70	131.54	33.52	9.21

In the bottom panel of Figure 2 we also present the quantum speed limit ${\tau }_{QSL}$ for the SE dynamics of a QE with ${\omega }_0=0.22379$ eV located at $d=5$ nm from a nanodisk of radius $R=30$ nm. In all cases, the quantum speed limit always attains a smaller value than the driving time, indicating that by exploiting the non-Markovianity of an open quantum system one can obtain speedup of the actual quantum dynamics in comparison to the corresponding dynamics under Markovian conditions.

4. Summary

In this work, we analyzed the SE dynamics of the excited state population of a QE modeled as a two-level system located at 5 nm from a graphene nanodisk of radius 30 nm, while the free-space decay time of the emitter lies between 100 picoseconds and microseconds. Strong coupling at the single QE and single photon level was found. We showed pronounced decaying Rabi oscillations and population trapping effects in the dynamical evolution of the excited state population of the QE and also quantified the non-Markovianity of the SE dynamics by computing different measures as well as the quantum speed limit for each case. These results are in agreement with the behavior of the QE excited state population dynamics under strong coupling conditions, giving large measures values and potentially large quantum speed-up for the dynamics.