Functional Gradients of the Gyroid Infill for Structural Optimization ^†

1. Introduction

Cellular structures allow the minimizing of the mass of a part while keeping its shape. For example, in additively manufactured parts, setting specific infill definitions allows for substantial material savings. Thus, in order to achieve material savings and structural performance, it is possible to use structural optimization techniques to vary the infill density spatially. Some examples of infill distribution optimization can be found in the following works: [1,2,3,4,5]

The infill shape chosen for this work is the gyroid infill, available in fused filament fabrication (FFF) slicers, such as PrusaSlicer, which was the slicer used in this work. The gyroid infill is an approximation of the gyroid foam, derived from the gyroid surface. In Figure 1, the gyroid infill is shown next to the gyroid foam.

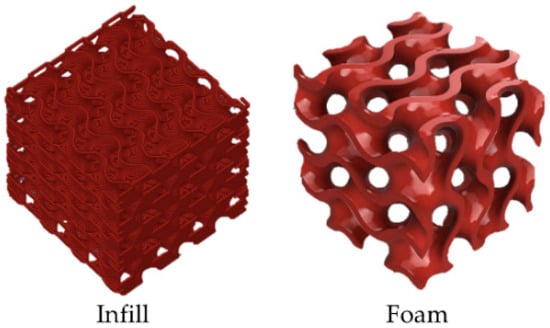
Figure 1. Gyroid infill and gyroid foam.

2. Materials and Methods

In this work, the gyroid infill was mechanically characterized through tensile and compressive tests [6], allowing us to obtain the Young’s modulus and ultimate stress, respectively, for different infill densities. With it, an experimental homogenization law was developed and implemented into a bio-inspired structural optimization algorithm [7], which defines the optimal density distribution based on a material law correlating the mechanical properties with the apparent density. Figure 2 shows a flowchart describing the considered bio-inspired remodeling algorithm (BIRA).

Figure 2. Flowchart of the BIRA.

Additionally, a conventional structural optimization algorithm, the bidirectional evolutionary structural optimization (BESO) [8], was used in order to compare the results of both approaches. The parameters used in the BESO were an increase ratio of 0.05 and a decrease ratio of 0.1. Two standard flexural load cases were studied, namely a three-point bending (3PB) load case and a four-point bending (4PB) load case. The design domain and load cases are further shown in Figure 3.

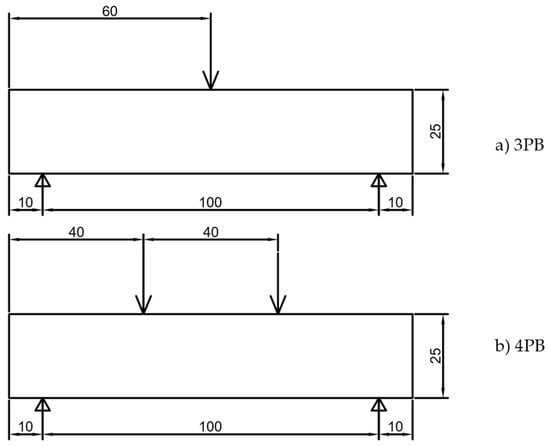
Figure 3. Design domain for both load cases.

In order to obtain physical specimens that can be tested, a post-processing stage was included. At this stage, the density field is divided into density groups corresponding to a maximum density, a transition density and a minimum density. The elements belonging to each group will be translated into an individual solid, so that an infill density in the slicing software can be attributed to each solid. In order to avoid abrupt density changes, which would decrease the connection between the solids, a smoothing stage is included. In this stage, the density is averaged with the density of the nearby elements, according to Equations (1) to (3), where w_ij is the weight, d_ij is the distance ratio, and ρⁱ_smooth is the new density of the element.

$$w_{ij}=1-d_{ij}$$

(1)

$$d_{ij}=\frac{dist\left(i,j\right)}{\max \left(dist\right)}.$$

(2)

$${\rho }_{smooth}^i=\frac{{\displaystyle \sum }{w}_{ij} {\rho }_i}{{\displaystyle \sum }{w}_{ij}}$$

(3)

3. Results

The results of the mechanical tests to obtain the mechanical properties of the gyroid infill are shown in Table 1.

Table 1. Mechanical properties of the gyroid infill used in the homogenization law.

Infill Density	Young’s Modulus (MPa)	Ultimate Stress (MPa)
20%	61	5
50%	258	20
80%	459	34

The structural optimization results are shown in Figure 4, which displays the density distribution results when the structure reduces to approximately 50% of its original mass, or an average apparent density of 0.6 g/cm³, because the density of PLA is 1.25 g/cm³.

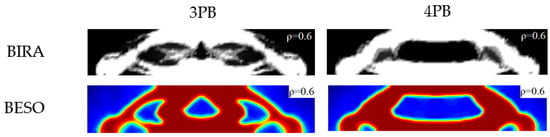
Figure 4. Structural optimization results.

Figure 5 shows the printed specimens in order to demonstrate the effect of the smoothing stage in the final specimen configuration.

Figure 5. Printed specimens.

The printed specimens were tested according to the load case defined in the optimization analysis. The test results are summarized in Table 2. In addition, uniformly infilled specimens with 50% gyroid infill density were printed and tested according to the same load cases for comparison purposes. The variable that was chosen to evaluate the structural behavior of the parts was its stiffness, calculated as shown in Equation (4), where F is the measured force, and d is the applied vertical displacement.

$$K=\frac{F \left[N\right]}{d \left[mm\right]}$$

(4)

Table 2. Stiffness values of the optimized parts.

	Load Case	Theoretical (N/mm)	Experimental (without Smoothing) (N/mm)	Experimental (with Smoothing)(N/mm)
BIRA	3PB	251	110.05 ± 0.5	150.04 ± 1.7
	4PB	364	304.65 ± 0.5	203.22 ± 3.8
BESO	3PB	-	83.77 ± 3.5	138.87 ± 1.2
	4PB	-	245.23 ± 6.7	143.42 ± 3.1
Uniform lattice	3PB	-	115.7 ± 2.0
	4PB	-	176.8 ± 5.6

4. Conclusions

The BIRA approach resulted in parts with higher stiffness than the parts obtained by the conventional structural optimization approach. The smoothing process presented a positive effect in the parts subjected to the 3PB load case. In the 4PB load case, the smoothing presented a negative effect, possibly because these are more optimized structures than the ones subjected to the first load case. Because of this, it can be suggested that the smoothing process can improve a structure with high stress concentration zones, such as thin bars, but it might have the opposite effect when the original structure is more robust. Except for the 3PB load case of structures without any smoothing, the optimized structures presented higher stiffness than the uniform lattice.