Modeling and Analysis of Hybrid Blood Nanofluid as Drug Carriers through Artery with Rheological Effects †
Abstract
1. Introduction
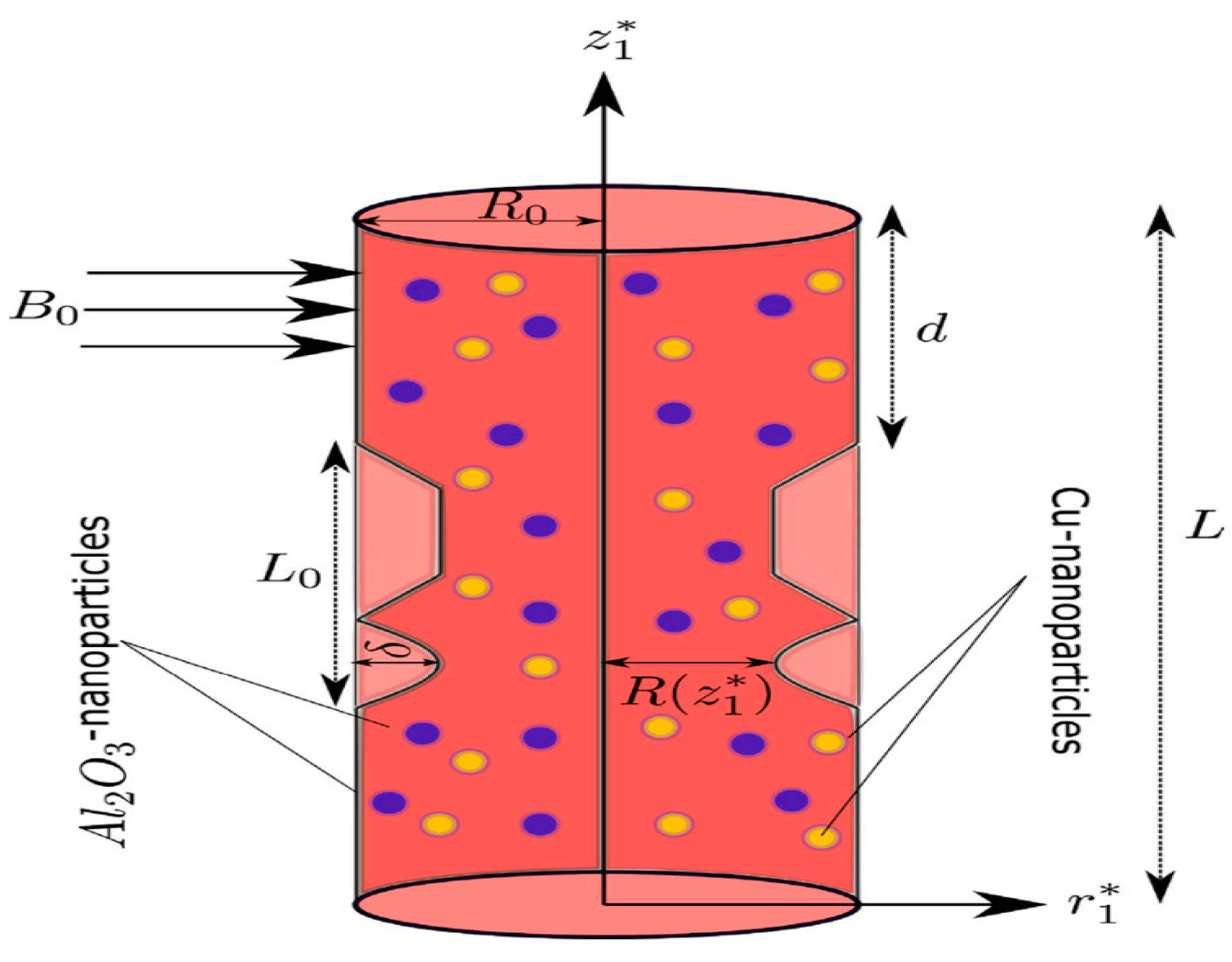
2. Geometry of the Flow
3. Mathematical Formulation
4. Nondimensionalization of the Model
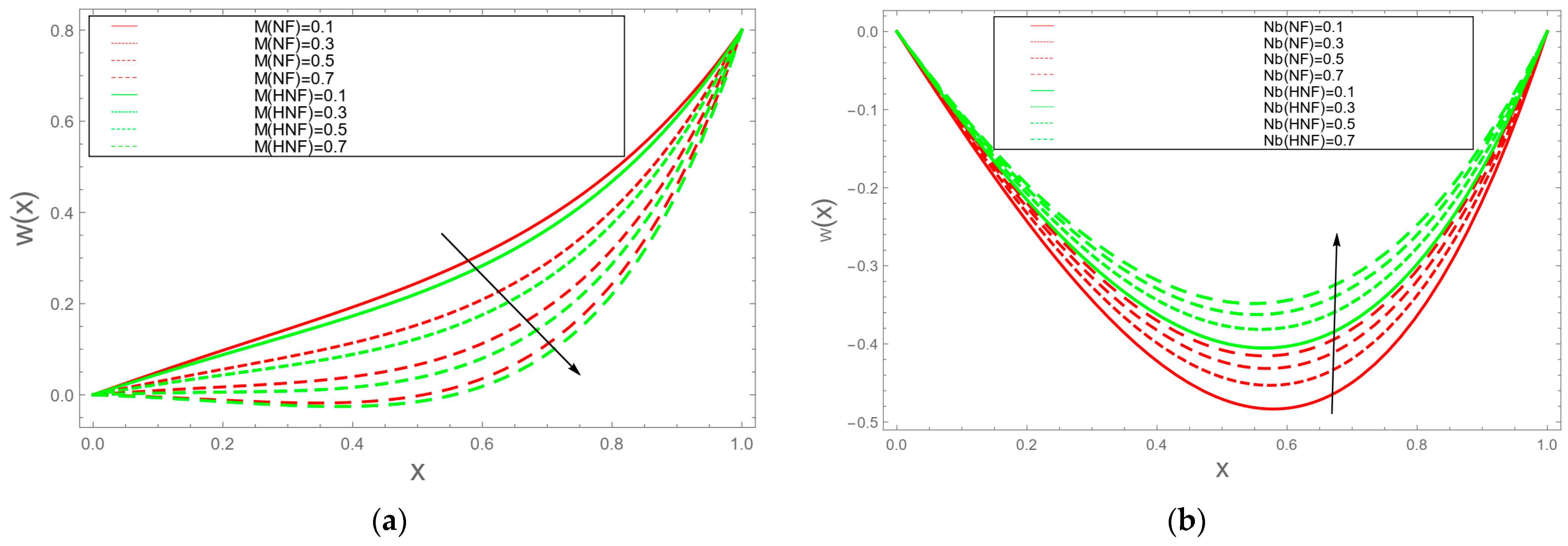
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Tripathi, J.; Vasu, B.; Bég, O.A.; Gorla, R.S.R. Unsteady hybrid nanoparticle-mediated magneto-hemodynamics and heat transfer through an overlapped stenotic artery: Biomedical drug delivery simulation. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 1175–1196. [Google Scholar] [CrossRef] [PubMed]
- Vasu, B.; Dubey, A.; Bég, O.A. Finite element analysis of non-Newtonian magnetohemodynamic flow conveying nanoparticles through a stenosed coronary artery. Heat Transf. Res. 2020, 49, 33–66. [Google Scholar]
- Nadeem, S.; Ijaz, S.; Sadiq, M.A. Inspiration of induced magnetic field on a blood flow of Prandtl nanofluid model with stenosis. Curr. Nanosci. 2014, 10, 753–765. [Google Scholar] [CrossRef]
- Bashaga, G.; Shaw, S. Shear-augmented solute dispersion during drug delivery for three-layer flow through microvessel under stress jump and momentum slip-Darcy model. Appl. Math. Mech. 2021, 42, 901–914. [Google Scholar] [CrossRef]
- Maiti, S.; Shaw, S.; Shit, G.C. Caputo–Fabrizio fractional order model on MHD blood flow with heat and mass transfer through a porous vessel in the presence of thermal radiation. Phys. A Stat. Mech. Its Appl. 2020, 540, 123149. [Google Scholar] [CrossRef]
- Roy, A.K.; Shaw, S. Shear augmented microvascular solute transport with a two-phase model: Application in nanoparticle assisted drug delivery. Phys. Fluids 2021, 33, 31904. [Google Scholar] [CrossRef]
- Dinarvand, S.; Rostami, M.N.; Dinarvand, R.; Pop, I. Improvement of drug delivery micro-circulatory system with a novel pattern of CuO-Cu/blood hybrid nanofluid flow towards a porous stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4408–4429. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.K.; Kumawat, C.; Beg, O.A. Modeling and analysis of magnetic hybrid nanoparticle (au-al 2 o 3/blood) based drug delivery through a bell-shaped occluded artery with joule heating, viscous dissipation and variable viscosity effects. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 2024–2043. [Google Scholar] [CrossRef]
- Srivastava, V.P.; Vishnoi, R.; Mishra, S.; Sinha, P. Blood flow through a composite stenosis in catheterized arteries. E-J. Sci. Technol. 2015, 55–64. [Google Scholar] [CrossRef]
- Dolui, S.; Bhaumik, B.; De, S. Combined effect of induced magnetic field and thermal radiation on ternary hybrid nanofluid flow through an inclined catheterized artery with multiple stenosis. Chem. Phys. Lett. 2023, 811, 140209. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.K.; Mishra, N.K.; Al-Mdallal, Q.M. Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials 2023, 13, 652. [Google Scholar] [CrossRef] [PubMed]
- Zaman, A.; Sajid, M.; Kousar, N. Biomedical study of effects nanoparticles on unsteady blood (non-Newtonian) flow through a catheterized stenotic vessel. Can. J. Phys. 2019, 97, 487–497. [Google Scholar] [CrossRef]
- Tripathi, J.; Vasu, B.; Dubey, A.; Gorla, R.S.; Murthy, P.V.S.N.; Bég, O.A.; Prasad, V.R.; Saikrishnan, P. A review on recent advancements in the hemodynamics of nano-drug delivery systems. Nanosci. Technol. An Int. J. 2020, 11, 73–98. [Google Scholar] [CrossRef]
- Ijaz, S.; Nadeem, S. Slip examination on the wall of tapered stenosed artery with emerging application of nanoparticles. Int. J. Therm. Sci. 2016, 109, 401–412. [Google Scholar] [CrossRef]
| Thermophysical Properties | |||||
|---|---|---|---|---|---|
| Blood | 1063 | 3594 | 0.492 | 0.667 | 0.18 |
| Copper | 8933 | 385 | 400 | 1.67 | |
| Aluminum Oxide () | 4970 | 765 | 40 | 0.85 |
| Radius | Ijaz and Nadeem [15] | Present Paper | Ijaz and Nadeem [15] | Present Paper |
|---|---|---|---|---|
| 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.2 | 0.0317 | 0.0318 | 0.0645 | 0.0647 |
| 0.3 | 0.0418 | 0.0420 | 0.0820 | 0.0823 |
| 0.4 | 0.0420 | 0.0422 | 0.0776 | 0.0779 |
| 0.5 | 0.0366 | 0.0369 | 0.0613 | 0.0616 |
| 0.6 | 0.0283 | 0.0286 | 0.0390 | 0.0393 |
| 0.7 | 0.0191 | 0.0193 | 0.0152 | 0.0162 |
| 0.8 | 0.0109 | 0.0109 | −0.0060 | −0.0063 |
| 0.9 | 0.0052 | 0.0054 | −0.0206 | −0.0206 |
| 1.0 | 0.0039 | 0.0040 | −0.0248 | −0.0249 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, T.; Shah, Z.; Rooman, M.; Ullah, H. Modeling and Analysis of Hybrid Blood Nanofluid as Drug Carriers through Artery with Rheological Effects. Mater. Proc. 2024, 17, 8. https://doi.org/10.3390/materproc2024017008
Zaman T, Shah Z, Rooman M, Ullah H. Modeling and Analysis of Hybrid Blood Nanofluid as Drug Carriers through Artery with Rheological Effects. Materials Proceedings. 2024; 17(1):8. https://doi.org/10.3390/materproc2024017008
Chicago/Turabian StyleZaman, Tahir, Zahir Shah, Muhammad Rooman, and Hamayat Ullah. 2024. "Modeling and Analysis of Hybrid Blood Nanofluid as Drug Carriers through Artery with Rheological Effects" Materials Proceedings 17, no. 1: 8. https://doi.org/10.3390/materproc2024017008
APA StyleZaman, T., Shah, Z., Rooman, M., & Ullah, H. (2024). Modeling and Analysis of Hybrid Blood Nanofluid as Drug Carriers through Artery with Rheological Effects. Materials Proceedings, 17(1), 8. https://doi.org/10.3390/materproc2024017008







