Multi-Objective MILP Models for Optimizing Makespan and Energy Consumption in Additive Manufacturing Systems †
Abstract
1. Introduction
2. Single-Machine Environment with Energy Considerations ()
2.1. Parameters and Variables
2.1.1. Part-Related Parameters
- : Height of part i (cm).
- : Area required by part i (cm2).
- : Volume of part i (cm3).
2.1.2. Machine-Related Parameters
- : Time spent to form per unit volume of material (hr/cm3).
- : Time spent for powder-layering per unit height (hr/cm).
- : Setup time needed for initializing and cleaning (hr).
- : Production area capacity of the machine’s tray (cm2).
- : Power consumption during printing operation (kW).
- : Power consumption during layer formation (kW).
- : Power consumption during setup operations (kW).
- : Power consumption during idle time (kW).
2.1.3. Decision Variables
- : Binary variable that equals 1 if part i is assigned to job j; 0 otherwise.
- : Binary variable that equals 1 if job j is utilized (i.e., at least one part is assigned to it); 0 otherwise.
- : Completion time of job j (hr).
- : Makespan, i.e., the maximum completion time among all jobs (hr).
- : Energy consumed during printing operations for job j (kWh).
- : Energy consumed during layer formation for job j (kWh).
- : Energy consumed during setup operations for job j (kWh).
- : Total energy consumption (kWh).
2.2. Mathematical Model
2.2.1. Objective Functions
2.2.2. Production Time Calculation
2.2.3. Energy Consumption Calculation
2.2.4. Constraints
- Part Occurrence Constraint
- Area Capacity Constraint
- Job Utilization Constraint
- Completion Time Constraints
- Makespan Constraint
- Total Energy Consumption
- Idle Energy Consumption
- Sign Constraints
2.2.5. Linearization of Maximum Function
2.3. Solution Approach
- Solving for optimal makespan ignoring energy considerations.
- Solving for optimal energy consumption ignoring makespan.
- Formulating the problem as follows:Subject to all constraints plus the following:where represents the acceptable tolerance for makespan degradation.
3. Computational Results and Analysis
3.1. Experimental Setup
3.1.1. Test Instances
- Set A (S1-S14): Small-sized instances with 6–12 parts on a single machine.
- Set B (P15-P38): Medium-sized instances with 15–46 parts on 2–3 parallel identical machines.
- Set C (R39-R62): Medium- to large-sized instances with 15–46 parts on 2–3 parallel non-identical machines.
3.1.2. Solution Approaches
- Makespan-only optimization: minimize (traditional approach).
- Energy-only optimization: minimize .
- Multi-objective optimization: using both weighted-sum and -constraint methods.
3.2. Results for Single-Machine Environment
3.3. Results for Parallel Identical Machines
3.4. Results for Parallel Non-Identical Machines
3.5. Analysis of Machine Assignment in Non-Identical Environment
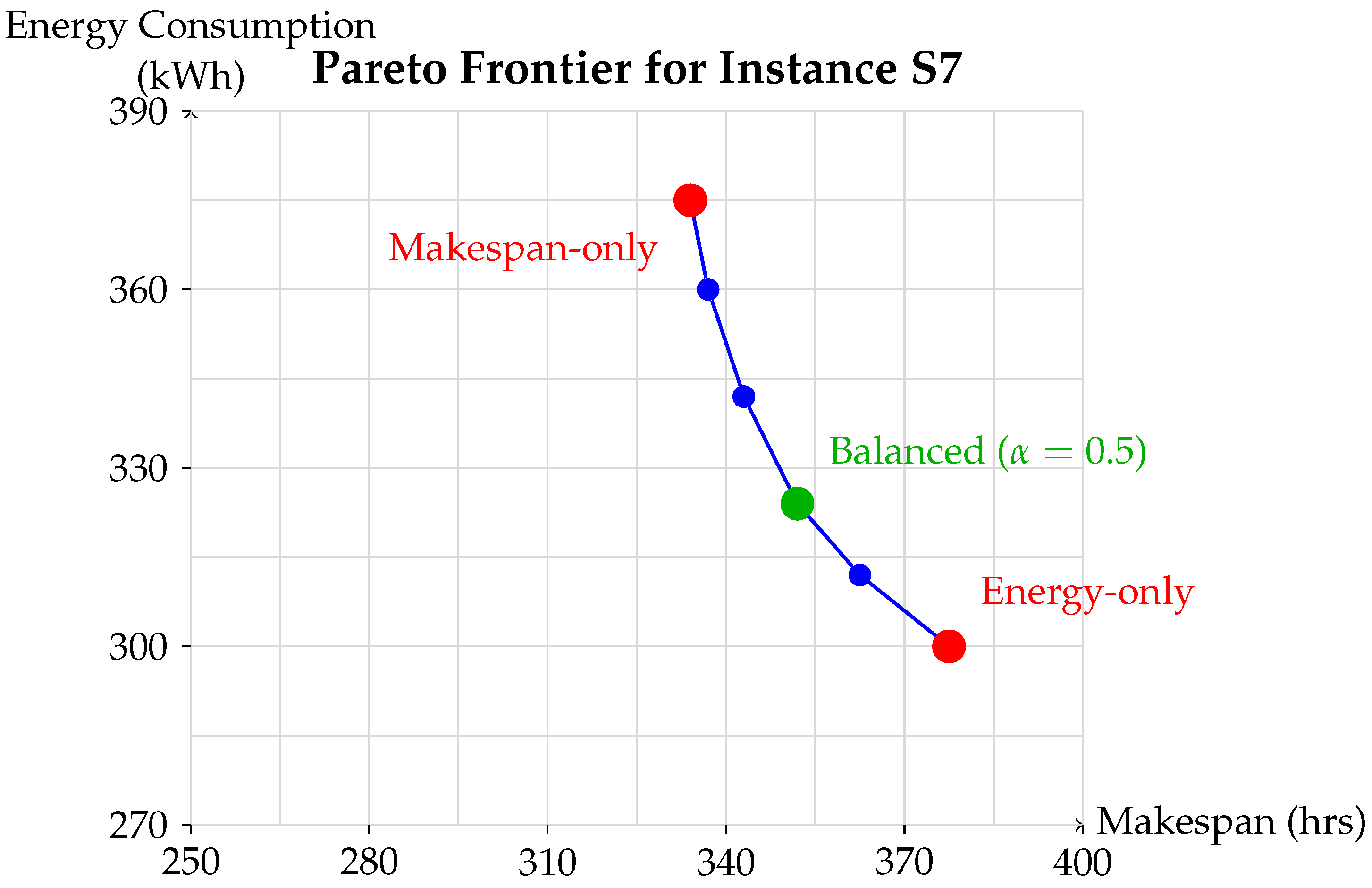
3.6. Impact of Weight Parameter in Multi-Objective Optimization
3.7. Comparison of Weighted-Sum and -Constraint Methods
3.8. Enhanced Load Balancing Strategy for Parallel Machines
3.9. Summary of Results
- Energy-only optimization can reduce energy consumption by 16–19% compared to makespan-only optimization, but at the cost of a 16–23% increase in makespan.
- Multi-objective optimization with balanced weights () achieves 12–14% energy savings with only a 4–5% increase in makespan.
- The energy savings are more pronounced in the parallel non-identical machine environment (14.1%) compared to the single-machine (12.0%) and parallel identical machine (12.2%) environments.
- The -constraint method generates more diverse Pareto-optimal solutions than the weighted-sum method but requires more computational effort.
- Enhanced load balancing for parallel machines can further reduce energy consumption by up to 6.4% with minimal impact on makespan.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weller, C.; Kleer, R.; Piller, F.T. Industrie 4.0 and the potential of additive manufacturing. Int. J. Prod. Econ. 2015, 164, 113–126. [Google Scholar]
- Li, W.; Zhang, Y.; Wang, B. Additive manufacturing scheduling optimization: A comprehensive review. J. Manuf. Sci. Eng. 2017, 139, 051017. [Google Scholar]
- Berman, B. 3-D printing: The new industrial revolution. Bus. Horizons 2012, 55, 155–162. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies: Rapid Prototyping to Direct Digital Manufacturing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vicari, A.; Williams, C.B. Economic analysis of additive manufacturing markets. Addit. Manuf. 2015, 8, 45–62. [Google Scholar]
- Marshall, J.A.; Harik, R. Case studies in aerospace additive manufacturing applications. Int. J. Adv. Manuf. Technol. 2017, 92, 365–378. [Google Scholar]
- Zhang, J.; Yao, X.; Li, D. Scheduling problems in additive manufacturing: A review and outlook. J. Manuf. Syst. 2018, 49, 14–27. [Google Scholar]
- Alici, G.; Li, W. A review of process planning and scheduling for additive manufacturing. Int. J. Prod. Res. 2016, 54, 2871–2897. [Google Scholar]
- Kucukkoc, I. Cost modeling and optimization of additive manufacturing systems. Robot. Comput.-Integr. Manuf. 2016, 37, 158–164. [Google Scholar]
- Kucukkoc, I.; Zhang, D.Z. MILP models for makespan minimization in AM batch scheduling. Int. J. Prod. Res. 2019, 57, 1234–1256. [Google Scholar]
- Kellens, K.; Baumers, M.; Gutowski, T.G.; Flanagan, W.; Lifset, R.; Duflou, J.R. Environmental impact of additive manufacturing processes: A review. J. Clean. Prod. 2017, 140, 1455–1468. [Google Scholar]
- Baumers, M.; Tuck, C.; Hague, R. Energy consumption in additive manufacturing. J. Ind. Ecol. 2011, 15, 660–668. [Google Scholar]
- Yosofi, M.; Kerbrat, O.; Mognol, P. Energy consumption optimization in additive manufacturing. J. Clean. Prod. 2019, 214, 881–890. [Google Scholar]
- Le, T.N.; Park, S.H. Energy consumption model for selective laser melting process. Int. J. Precis. Eng. Manuf.-Green Technol. 2015, 2, 243–251. [Google Scholar]
- Luo, Y.; Ji, Z.; Leu, M.C.; McDonald, T.P. Sustainable additive manufacturing: A review of environmental aspects, energy efficiency and socio-economic impacts. Addit. Manuf. 2019, 28, 1–23. [Google Scholar]
- Chekurov, S.; Metsä-Kortelainen, S.; Salmi, M.; Roda, I.; Cataudella, V.; Jacucci, G. Additive manufacturing: Challenges from the process scheduling perspective. Procedia CIRP 2018, 67, 236–241. [Google Scholar]
- Fera, M.; Fruggiero, F.; Lambiase, A.; Macchiaroli, R. Multi-objective optimization for energy consumption and makespan in additive manufacturing scheduling. J. Clean. Prod. 2020, 248, 119256. [Google Scholar]


| Machine Type | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (hr/cm3) | (hr/cm) | (hr) | (cm2) | (cm) | (kW) | (kW) | (kW) | (kW) | |
| Standard | 0.030864 | 0.7 | 1.0 | 900 | 40 | 1.2 | 0.8 | 0.5 | 0.15 |
| High-Speed | 0.025720 | 0.6 | 1.2 | 800 | 35 | 1.5 | 1.0 | 0.6 | 0.18 |
| Large-Format | 0.032400 | 0.8 | 1.5 | 1200 | 50 | 1.8 | 1.2 | 0.7 | 0.20 |
| Instance | Parts | Makespan Optimization | Energy Optimization | Multi-Objective () | |||||
|---|---|---|---|---|---|---|---|---|---|
| Time(s) | Time(s) | ||||||||
| S1 | 6 | 201.36 | 245.82 | 4.80 | 232.57 | 203.68 | 5.12 | 212.44 | 212.53 |
| S2 | 6 | 198.83 | 237.40 | 4.90 | 229.75 | 196.12 | 5.34 | 208.19 | 205.83 |
| S3 | 7 | 181.23 | 218.68 | 5.20 | 208.41 | 178.91 | 5.56 | 191.20 | 186.24 |
| S4 | 7 | 173.83 | 210.33 | 5.20 | 199.90 | 172.47 | 5.67 | 177.31 | 183.56 |
| S5 | 8 | 190.96 | 232.97 | 5.00 | 219.60 | 195.69 | 5.42 | 197.89 | 202.43 |
| S6 | 8 | 183.55 | 222.09 | 5.00 | 210.48 | 180.90 | 5.35 | 191.88 | 190.45 |
| S7 | 9 | 266.10 | 324.64 | 5.50 | 305.18 | 271.91 | 5.82 | 278.07 | 286.55 |
| S8 | 9 | 254.00 | 308.35 | 5.30 | 289.56 | 256.94 | 5.61 | 261.62 | 270.89 |
| S9 | 10 | 283.03 | 344.05 | 5.30 | 325.49 | 290.20 | 5.74 | 295.96 | 305.68 |
| S10 | 10 | 275.62 | 336.26 | 5.10 | 320.00 | 285.21 | 5.45 | 290.16 | 298.97 |
| S11 | 11 | 374.22 | 456.55 | 5.20 | 432.72 | 394.60 | 5.58 | 392.93 | 412.48 |
| S12 | 11 | 364.85 | 446.13 | 5.20 | 423.23 | 384.62 | 5.52 | 380.24 | 398.31 |
| S13 | 12 | 538.09 | 657.47 | 5.00 | 616.63 | 562.19 | 5.36 | 562.71 | 591.22 |
| S14 | 12 | 528.12 | 644.72 | 7.70 | 607.34 | 551.23 | 8.12 | 552.08 | 578.42 |
| Average | - | 271.70 | 334.68 | 5.31 | 315.63 | 280.33 | 5.69 | 285.19 | 294.54 |
| Improvement | - | - | - | - | −16.2% | 16.2% | - | −5.0% | 12.0% |
| Instance | Parts | Machines | Makespan Optimization | Energy Optimization | Multi-Objective () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time(s) | Time(s) | Time(s) | |||||||||
| P15 | 15 | 2 | 197.51 | 388.65 | 8.20 | 234.07 | 316.29 | 10.53 | 206.40 | 332.54 | 15.47 |
| P19 | 18 | 2 | 381.17 | 747.09 | 9.90 | 451.78 | 620.08 | 13.45 | 397.38 | 652.84 | 21.82 |
| P23 | 22 | 2 | 414.32 | 814.18 | 18.50 | 485.75 | 675.77 | 24.36 | 426.75 | 708.34 | 36.73 |
| P27 | 25 | 2 | 438.41 | 862.63 | 294.30 | 516.32 | 712.60 | 356.18 | 459.30 | 744.86 | 487.52 |
| P31 | 30 | 3 | 341.51 | 1007.45 | 12.20 | 409.81 | 852.30 | 17.42 | 358.59 | 896.62 | 25.67 |
| P33 | 36 | 3 | 368.68 * | 1071.07 * | 1800.00 | 445.11 * | 905.55 * | 1800.00 | 387.11 * | 951.25 * | 1800.00 |
| P35 | 38 | 3 | 361.05 * | 1047.05 * | 1800.00 | 432.54 * | 883.15 * | 1800.00 | 379.10 * | 926.83 * | 1800.00 |
| P37 | 46 | 3 | 435.71 * | 1267.91 * | 1800.00 | 526.21 * | 1061.04 * | 1800.00 | 457.50 * | 1116.16 * | 1800.00 |
| Average | - | - | 367.30 | 900.75 | 717.89 | 437.70 | 753.35 | 727.74 | 384.00 | 791.18 | 748.40 |
| Improvement | - | - | - | - | - | −19.2% | 16.4% | - | −4.5% | 12.2% | - |
| Instance | Parts | Machines | Makespan Optimization | Energy Optimization | Multi-Objective () | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time(s) | Time(s) | Time(s) | |||||||||
| R39 | 15 | 2 | 195.44 | 398.68 | 5.80 | 238.43 | 318.94 | 8.45 | 206.16 | 339.88 | 14.67 |
| R43 | 18 | 2 | 372.58 | 789.87 | 7.40 | 458.27 | 647.69 | 10.83 | 391.21 | 681.29 | 18.54 |
| R47 | 22 | 2 | 425.93 | 911.49 | 26.20 | 536.67 | 738.31 | 35.47 | 447.23 | 787.93 | 48.76 |
| R51 | 25 | 3 | 296.05 | 893.08 | 48.90 | 362.10 | 714.46 | 68.46 | 310.85 | 759.11 | 93.48 |
| R55 | 30 | 3 | 342.30 * | 1062.77 * | 2400.00 | 418.61 * | 851.54 * | 2400.00 | 359.42 * | 902.35 * | 2400.00 |
| R57 | 36 | 3 | 374.05 * | 1160.22 * | 2400.00 | 457.34 * | 942.78 * | 2400.00 | 392.75 * | 1003.97 * | 2400.00 |
| R59 | 38 | 3 | 364.62 * | 1144.91 * | 2400.00 | 445.84 * | 932.89 * | 2400.00 | 379.20 * | 990.13 * | 2400.00 |
| R61 | 46 | 3 | 443.71 * | 1386.39 * | 2400.00 | 540.53 * | 1123.98 * | 2400.00 | 465.90 * | 1192.29 * | 2400.00 |
| Average | - | - | 351.84 | 968.43 | 1211.04 | 432.22 | 783.82 | 1215.40 | 369.09 | 832.12 | 1221.93 |
| Improvement | - | - | - | - | - | −22.8% | 19.1% | - | −4.9% | 14.1% | - |
| Instance | Weighted-Sum | -Constraint | Unique Solutions |
|---|---|---|---|
| S7 | 4 | 5 | 6 |
| P19 | 3 | 4 | 5 |
| R47 | 3 | 4 | 4 |
| Imbalance Parameter | Max Load Difference (%) | ||
|---|---|---|---|
| No constraint | 414.32 | 814.18 | 37.2% |
| 417.85 | 792.44 | 28.6% | |
| 423.61 | 775.89 | 19.8% | |
| 432.18 | 762.47 | 9.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saaad, S.; Touil, A.; Oucheikh, R. Multi-Objective MILP Models for Optimizing Makespan and Energy Consumption in Additive Manufacturing Systems. Eng. Proc. 2025, 97, 28. https://doi.org/10.3390/engproc2025097028
Saaad S, Touil A, Oucheikh R. Multi-Objective MILP Models for Optimizing Makespan and Energy Consumption in Additive Manufacturing Systems. Engineering Proceedings. 2025; 97(1):28. https://doi.org/10.3390/engproc2025097028
Chicago/Turabian StyleSaaad, Safae, Achraf Touil, and Rachid Oucheikh. 2025. "Multi-Objective MILP Models for Optimizing Makespan and Energy Consumption in Additive Manufacturing Systems" Engineering Proceedings 97, no. 1: 28. https://doi.org/10.3390/engproc2025097028
APA StyleSaaad, S., Touil, A., & Oucheikh, R. (2025). Multi-Objective MILP Models for Optimizing Makespan and Energy Consumption in Additive Manufacturing Systems. Engineering Proceedings, 97(1), 28. https://doi.org/10.3390/engproc2025097028







