A Parallel Processing Architecture for Long-Term Power Load Forecasting ^†

Abstract

The increasing complexity of power grids and integration of renewable energy sources necessitate accurate power load forecasting across multiple time horizons. While existing methods have advanced significantly, they often struggle with consistent performance across different prediction ranges, leading to suboptimal resource allocation. We propose MP-RWKV (Multi-Path Recurrent Weighted Key–Value), an enhanced architecture that builds upon RWKV-TS and addresses these challenges through parallel processing paths for temporal modeling. Our model maintains robust performance across both short-term and long-term forecasting scenarios through its context state mechanism and position-aware attention. Evaluated on extensive power load data, MP-RWKV demonstrates superior performance over state-of-the-art baselines, including Transformer-based models and LSTM variants. The model achieves the lowest Mean Absolute Error (MAE) across prediction horizons ranging from 24 h to 432 h, showing particular strength in maintaining consistent accuracy where traditional models deteriorate. Notably, MP-RWKV successfully balances immediate temporal correlations with extended dependencies, offering promising implications for power grid management and sustainable energy systems. The model’s stable performance across varying prediction horizons makes it particularly suitable for real-world power load forecasting applications.

1. Introduction

The world energy landscape is transforming due to a gradual increase in electricity consumption over the years, which is forecast to reach historic levels in the next few decades [1]. The increased demand for renewable energy sources and smart grid technology has led to a greater need for reliable long-term power load forecasts. Accurate forecasting is essential for the efficient planning of resources, the development of infrastructure, and the maintenance of the stability and reliability of power systems [2].

Long-term load forecasting (LTLF) poses particular challenges compared to short-term forecasting. It requires models that can handle short-term fluctuations as well as long-term trends induced by economic growth, technological advancements and climate change [3]. Although traditional forecasting methods are good for their simplicity and interpretability, they are ineffective in handling the complexity and non-linearity associated with long-term power load patterns [4].

This indicates that significant developments have been made in power load forecasting methodologies. The initial approach was largely statistical, with the majority using autoregressive integrated moving average (ARIMA) models [5]. While these models are effective for stationary time series, they are highly limited when it comes to handling the non-stationarity and non-linearity of long-term power load data [6].

This completely changed the dynamics of forecasting. Improvements in AI techniques and machine learning have enhanced the architecture of neural networks, particularly RNNs and LSTM networks, which have a greater ability to capture time dependencies [7]. However, these models have been shown to degrade over larger time horizons due to issues such as vanishing gradients [8].

In recent years, attention-based models have emerged, inspired by advances in natural language processing. These models, as exemplified by the Transformer model, appear to have potential for modeling long-range dependencies [9]. However, they are sometimes insensitive to local patterns that are important in power load dynamics [10].

Despite these advances, a significant gap remains in successfully blending the strengths of various modeling techniques for LTLF. No matter how advanced they are, standalone models tend not to accommodate the entire range of factors that contribute to long-term power load patterns [11]. Recent advances in neural architectures have shown promise in addressing these limitations. Long-term load forecasting has been approached through hierarchical neural models with time integrators [12], while machine learning techniques have been applied to traffic classification and prediction tasks [13]. Additionally, recurrent neural networks have been successfully applied to long-term generating power forecasting for wind power systems [14].

To address this issue, we propose a model called MP-RWKV-TS. As an improvement on the efficient RWKV-TS framework [15], it combines the advantages of recurrent networks’ good fit in short-term correlations with transformer-based models’ good fit in long-range dependence capabilities.

Our work makes a number of significant contributions to the field of long-term power load forecasting:

• We introduce MP-RWKV-TS, a combined model that extends the capabilities of RWKV-TS by utilizing parallel computation paths to identify both temporal patterns and cross-variable relationships.
• We utilize an Adaptive Time-Mixing Operator (ATMO) to enhance the model’s temporal variable dependency strength across timescales.
• Our approach incorporates a Cross-Variable Attention (CVA) mechanism that operates in parallel with temporal processing, enabling the modeling of complex interactions between factors affecting power load.
• We conduct thorough and detailed experiments on real-world data from a North African urban power grid distribution network, demonstrating the advantages of MP-RWKV-TS in long-term forecasting scenarios.
• We also introduce the interpretability aspects of the model to provide greater insight into the factors responsible for long-term power load dynamics.

The rest of this paper is organized as follows: Section 2 formulates the problem, Section 3 details our proposed MP-RWKV model, Section 4 presents the experimental results, and Section 5 concludes the paper.

2. Problem Formulation

Let $\mathcal{D}$ denote a dataset spanning N years containing both power load measurements and associated meteorological variables. We define the following:

2.1. Input Variables

For any time step t and dayd:

2.1.1. Weather Variables

Let ${\mathbf{W}}_{t,d}\in {\mathbb{R}}^M$ denote the weather feature vector:

$${\mathbf{W}}_{t,d}={[{\mathrm{Temp}}_{t,d},{\mathrm{Hum}}_{t,d},{\mathrm{Ws}}_{t,d}]}^T$$

where

• ${\mathrm{Temp}}_{t,d}\in \mathbb{R}$ represents temperature;
• ${\mathrm{Hum}}_{t,d}\in \mathbb{R}$ represents humidity;
• ${\mathrm{Ws}}_{t,d}\in \mathbb{R}$ represents wind speed.

2.1.2. Power Load

Let $P_{t,d}\in \mathbb{R}$ denote the power load at time step t of day d.

2.2. Temporal Modeling

Given a temporal context window $\tau$, we construct the input feature vector ${\mathbf{x}}_{t,d}$ as

$${\mathbf{x}}_{t,d}=[{\mathbf{P}}_{t-\tau :t-1,d};{\mathbf{W}}_{t-\tau :t-1,d}]\in {\mathbb{R}}^{(\tau \times (M+1\left)\right)}$$

where

• ${\mathbf{P}}_{t-\tau :t-1,d}=[P_{t-\tau ,d},...,P_{t-1,d}]$ represents historical load values;
• ${\mathbf{W}}_{t-\tau :t-1,d}=[{\mathbf{W}}_{t-\tau ,d},...,{\mathbf{W}}_{t-1,d}]$ represents historical weather conditions.

2.3. Prediction Objective

The forecasting task can be formulated as learning a function f:

$${\widehat{P}}_{t,d}=f({\mathbf{x}}_{t,d};\theta )$$

where

• ${\widehat{P}}_{t,d}$ is the predicted power load;
• $\theta$ represents the model parameters;
• $f:{\mathbb{R}}^{(\tau \times (M+1\left)\right)}\to \mathbb{R}$ is the prediction function.

The objective is to minimize the prediction error:

$$\underset{\theta }{min}\mathcal{L}(P_{t,d},{\widehat{P}}_{t,d})$$

where $\mathcal{L}$ is an appropriate loss function measuring the discrepancy between predicted and actual power load values.

3. The Proposed Model

3.1. Theoretical Foundation

The MP-RWKV architecture extends the RWKV-TS model [15] by incorporating principles of parallel information processing inspired by cognitive science theories. While maintaining the core efficiency of RWKV-TS, our enhanced model introduces parallel processing paths to concurrently handle different aspects of temporal data. This approach allows the model to simultaneously process temporal patterns and cross-variable dependencies, similar to how biological systems process sequential and relational information.

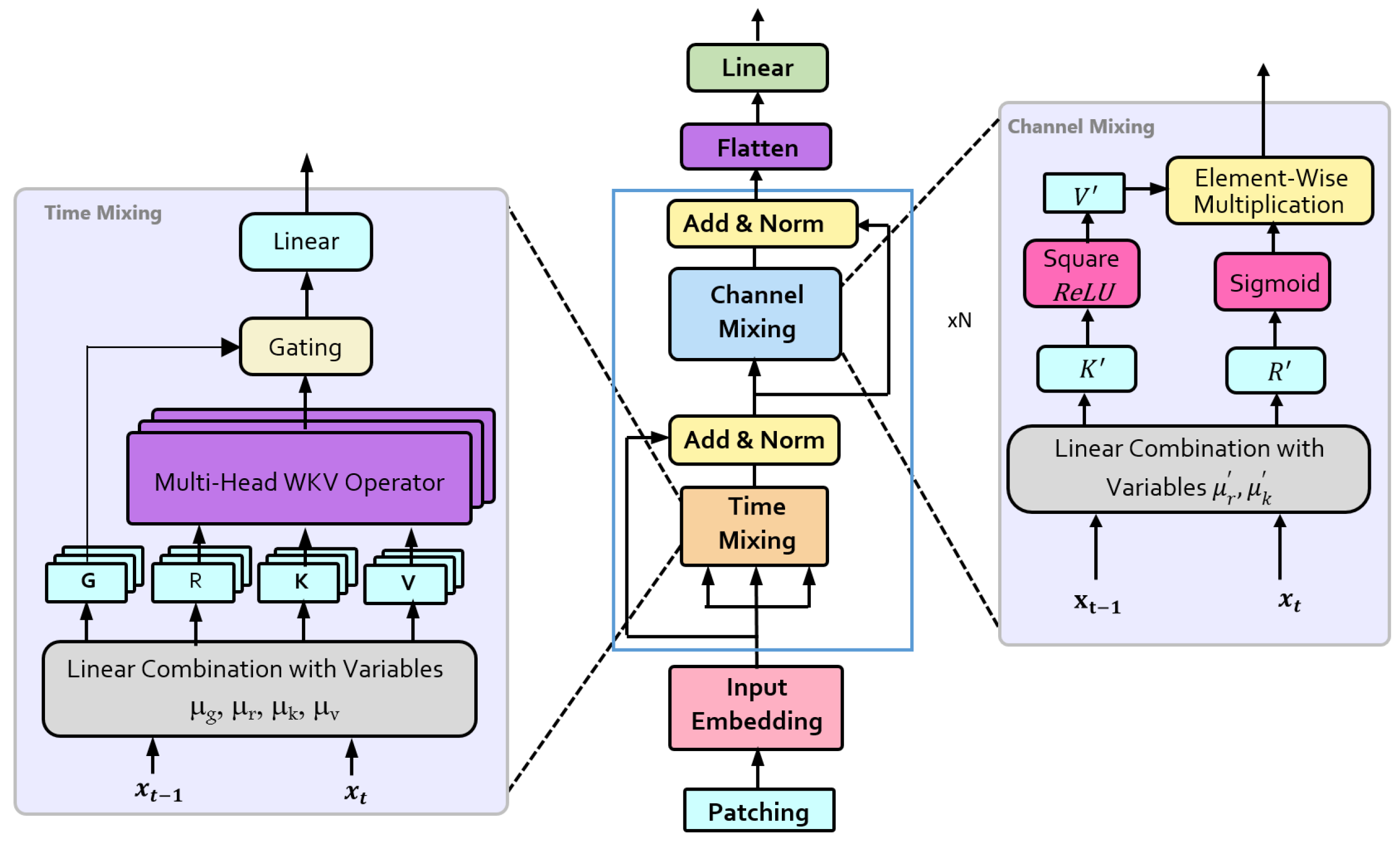
Figure 1 illustrates the foundational RWKV-TS architecture that serves as the basis for our enhanced MP-RWKV model.

3.2. Input Processing and Representation

Consider a multivariate time series $\mathbf{x}\in {\mathbb{R}}^{L\times M}$, where L represents the sequence length and M denotes the number of variables. The input processing consists of three critical stages:

3.2.1. Instance Normalization

To ensure numerical stability and consistent gradient flow, each univariate sequence undergoes instance normalization:

$${\mathbf{x}}_i={\displaystyle \frac{{\mathbf{x}}_i-\mathrm{mean}\left({\mathbf{x}}_i\right)}{\mathrm{std}\left({\mathbf{x}}_i\right)}}$$

where ${\mathbf{x}}_i\in {\mathbb{R}}^L$ represents the i-th variable sequence.

3.2.2. Patch Segmentation

The normalized sequence is segmented into overlapping patches to capture local temporal structures:

$$N=⌊{\displaystyle \frac{L-P}{S}}⌋+2$$

where P denotes patch length and S represents stride length. This segmentation creates patches ${\mathbf{x}}_i^p\in {\mathbb{R}}^{N\times P}$.

3.2.3. Token Projection

The projection phase maps the segmented patches into a high-dimensional feature space through a learned linear transformation. Given patches ${\mathbf{x}}_i^p\in {\mathbb{R}}^{N\times P}$, where N denotes the number of patches and P represents the patch length, the projection is formulated as follows:

$${\mathbf{x}}_i^t={\mathbf{x}}_i^p{\mathbf{W}}_p$$

where ${\mathbf{W}}_p\in {\mathbb{R}}^{P\times D}$ is a learnable projection matrix that transforms the input to dimension D. This transformation enables the model to learn rich feature representations while preserving temporal relationships within the sequence. The projected tokens ${\mathbf{x}}_i^t\in {\mathbb{R}}^{N\times D}$ serve as the foundation for subsequent temporal and cross-variable processing in the multi-path architecture.

3.3. Parallel Path Processing

Consider a multivariate time series ${\left\{{\mathbf{x}}_t\right\}}_{t=1}^T$, where ${\mathbf{x}}_t\in {\mathbb{R}}^D$ represents the input embedding at time step t. The enhanced architecture decomposes temporal processing into two complementary paths: a temporal path for sequential pattern extraction and a channel path for cross-variable dependency modeling. This decomposition enables specialized processing while maintaining parameter efficiency through strategic weight sharing.

As shown in Figure 2, our MP-RWKV architecture introduces parallel processing pathways that enable specialized handling of temporal patterns and cross-variable relationships.

3.3.1. Time-Mixing Path

The temporal path implements sequential pattern extraction through a hierarchical process consisting of adaptive mixing and position-aware attention mechanisms.

Adaptive Time-Mixing Operator (ATMO)

The ATMO computes dynamic interpolation coefficients to adaptively balance temporal dependencies:

$${\mathit{\mu }}_t=\sigma \left({\mathbf{W}}_{\mu }{\mathbf{x}}_t\right)\in {\mathbb{R}}^{2D}$$

where ${\mathbf{W}}_{\mu }\in {\mathbb{R}}^{2D\times D}$ defines the mixing transformation and $\sigma (·)$ ensures the coefficients lie in $(0,1)$. The temporal representations are then computed through weighted interpolation:

$$[{\mathbf{k}}_t^T,{\mathbf{v}}_t^T]={\mathbf{W}}_{kv}({\mathit{\mu }}_t[1:D]\odot {\mathbf{x}}_t+(1-{\mathit{\mu }}_t[1:D])\odot {\mathbf{x}}_{t-1})$$

where ${\mathbf{W}}_{kv}\in {\mathbb{R}}^{D\times 2D}$ projects the interpolated state into key–value pairs. This formulation enables the model to dynamically adjust the influence of recent and historical information.

Time-Aware Attention

The temporal context is integrated through position-sensitive attention:

$${\mathbf{c}}_t^T=\mathrm{TimeAwareAttention}({\mathbf{k}}_t^T,{\mathbf{v}}_t^T,t)$$

with the attention mechanism defined as

$$\mathrm{TimeAwareAttention}(\mathbf{k},\mathbf{v},t)=\mathrm{softmax}\left({\displaystyle \frac{{\mathbf{k}}^T\mathbf{k}}{\sqrt{d_k}}}+{\mathbf{T}}_t\right)\mathbf{v}$$

The temporal bias matrix ${\mathbf{T}}_t=\mathrm{TemporalBias}\left(t\right)\in {\mathbb{R}}^{D\times D}$ encodes relative positional information, enabling the model to capture position-dependent patterns in the sequence.

3.3.2. Channel-Mixing Path

The channel path focuses on modeling relationships between variables through parameter-efficient transformations and gated attention mechanisms.

Cross-Variable Processing

The channel-specific representations leverage the latter half of the mixing coefficients:

$$[{\mathbf{k}}_t^C,{\mathbf{v}}_t^C]={\mathbf{W}}_{kv}({\mathit{\mu }}_t[D+1:]\odot {\mathbf{x}}_t)$$

This formulation shares the projection matrix ${\mathbf{W}}_{kv}$ with the temporal path, promoting parameter efficiency while maintaining representational capacity.

Channel-Aware Attention

Cross-variable dependencies are modeled through a gated attention mechanism:

$${\mathbf{c}}_t^C=\mathrm{ChannelAwareAttention}({\mathbf{k}}_t^C,{\mathbf{v}}_t^C,{\mathbf{g}}_t^C)$$

defined as

$$\mathrm{ChannelAwareAttention}(\mathbf{k},\mathbf{v},\mathbf{g})=\mathrm{softmax}\left({\displaystyle \frac{{\mathbf{k}}^T\mathbf{k}}{\sqrt{d_k}}}\odot \mathbf{g}\right)\mathbf{v}$$

where ${\mathbf{g}}_t^C\in {\mathbb{R}}^D$ serves as an adaptive gating mechanism that modulates attention weights based on the relative importance of different variables. The scaling factor $\sqrt{d_k}$ ensures stable gradient propagation during training.

3.4. Path Integration and Output Generation

The integration of temporal and channel paths is achieved through an adaptive fusion mechanism that dynamically balances their contributions while maintaining residual connections to the input signal.

Adaptive Path Fusion

Let ${\mathbf{o}}_t^{TM}\in {\mathbb{R}}^D$ and ${\mathbf{o}}_t^{CM}\in {\mathbb{R}}^D$ denote the outputs from temporal and channel paths, respectively. The fusion mechanism computes dynamic weights through

$${\alpha }_t=\sigma \left({\mathbf{W}}_{\alpha }[{\mathbf{o}}_t^{TM};{\mathbf{o}}_t^{CM}]\right)\in {\mathbb{R}}^D$$

where ${\mathbf{W}}_{\alpha }\in {\mathbb{R}}^{D\times 2D}$ is a learnable projection matrix and $[·;·]$ denotes concatenation.

The paths are integrated through weighted combination with residual connection:

$${\mathbf{o}}_t={\alpha }_t\odot {\mathbf{o}}_t^{TM}+(1-{\alpha }_t)\odot {\mathbf{o}}_t^{CM}+{\mathbf{x}}_t$$

This formulation ensures that the model can adaptively prioritize temporal or cross-variable patterns while maintaining access to the original input features.

3.5. Advancing upon RWKV-TS

Our MP-RWKV model builds upon the foundation established by RWKV-TS [15], introducing several enhancements that specifically address the challenges of long-term power load forecasting:

• Parallel processing paths: While RWKV-TS processes all variables through a single computational path, MP-RWKV introduces parallel processing paths that enable specialized handling of temporal patterns and cross-variable relationships simultaneously. This allows the model to maintain the computational efficiency of RWKV-TS while expanding its representational capacity.
• Cross-Variable Attention (CVA): MP-RWKV enhances the original model with a dedicated path for modeling relationships between different variables through a specialized attention mechanism. This is particularly crucial for power load forecasting, where interactions between meteorological factors and temporal indicators significantly impact prediction accuracy.
• Adaptive path integration: Unlike the single-path processing in RWKV-TS, our model dynamically balances the contributions of temporal and cross-variable information based on the forecasting context, leading to more adaptive and robust predictions across varying horizons.
• Enhanced gradient flow: By separating concerns into parallel paths, MP-RWKV mitigates potential gradient issues that can affect single-path recurrent models when dealing with long-term dependencies.

These enhancements maintain the computational efficiency that makes RWKV-TS attractive while extending its capability to handle the complex temporal and cross-variable relationships present in power load data across multiple time scales.

3.6. Training Objective

The model is optimized through a composite objective function that combines reconstruction accuracy with temporal consistency:

$$\mathcal{L}\left(\theta \right)={\mathcal{L}}_{MSE}\left(\theta \right)+\lambda {\mathcal{L}}_{temporal}\left(\theta \right)$$

where $\theta$ denotes the model parameters and $\lambda >0$ is a hyperparameter controlling the trade-off between objectives.

The mean-squared error term measures prediction accuracy:

$${\mathcal{L}}_{MSE}\left(\theta \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\parallel y_i-{\widehat{y}}_i\parallel }_2^2$$

where $y_i$ and ${\widehat{y}}_i$ represent the ground truth and predicted values, respectively.

The temporal regularization term promotes smoothness in the temporal representations:

$${\mathcal{L}}_{temporal}\left(\theta \right)={\parallel {\mathbf{o}}_t^{TM}-{\mathbf{o}}_{t-1}^{TM}\parallel }_2$$

This regularization encourages the model to learn continuous temporal patterns while allowing for abrupt changes when supported by the data.

The optimization problem can be formally stated as

$${\theta }^{*}=argmi{n}_{\theta }\mathcal{L}\left(\theta \right)$$

solved through stochastic gradient descent with adaptive moment estimation:

$${\theta }_{t+1}={\theta }_t-\eta ·{\displaystyle \frac{{\widehat{m}}_t}{\sqrt{{\widehat{v}}_t}+ϵ}}$$

where ${\widehat{m}}_t$ and ${\widehat{v}}_t$ are bias-corrected first- and second-moment estimates of the gradients.

3.7. Complexity Analysis

We analyze the computational and space complexity of MP-RWKV-TS in terms of sequence length L and feature dimension D. The analysis considers both the forward pass computation and memory requirements.

Table 1. Computational and space complexity comparison.

Model	Time Complexity	Space Complexity	Parallelizable
Transformer	$\mathcal{O}\left(L^{2}D\right)$	$\mathcal{O}(L^2+LD)$	Yes
RNN	$\mathcal{O}\left(L{D}^2\right)$	$\mathcal{O}\left(D\right)$	No
LSTM	$\mathcal{O}\left(L{D}^2\right)$	$\mathcal{O}\left(D\right)$	No
MP-RWKV-TS	$\mathcal{O}\left(L{D}^2\right)$	$\mathcal{O}(LD+D^2)$	Partial

presents the computational and space complexity analysis for different sequence models, where L represents sequence length and D represents feature dimension. While Transformers offer full parallelization, they suffer from quadratic complexity in sequence length. Recurrent models like RNN and LSTM have linear time complexity but cannot be parallelized. Our proposed MP-RWKV-TS model achieves linear time complexity while supporting partial parallelization, offering a balanced trade-off between efficiency and computational requirements.

4. Experiments

Extensive experimentation on diverse time series datasets was conducted to validate the effectiveness of MP-RWKV in temporal pattern recognition and forecasting tasks. The model is systematically evaluated against state-of-the-art architectures, including RWKV-TS, Transformer variants, and traditional forecasting methods, using three complementary performance metrics: mean-squared error (MSE) to quantify prediction accuracy with emphasis on larger deviations, Mean Absolute Error (MAE) to assess absolute prediction differences, and Mean Absolute Percentage Error (MAPE) to measure relative accuracy across different scales. Furthermore, comprehensive ablation studies were performed to analyze the individual contributions of key architectural components, including the Adaptive Time-Mixing Operator, Cross-Variable Attention mechanism, and multi-path integration strategy. This rigorous evaluation framework demonstrates the superiority of MP-RWKV in capturing complex temporal and cross-variable dependencies while providing insights into the model’s interpretability and the effectiveness of its architectural enhancements.

4.1. Dataset Description

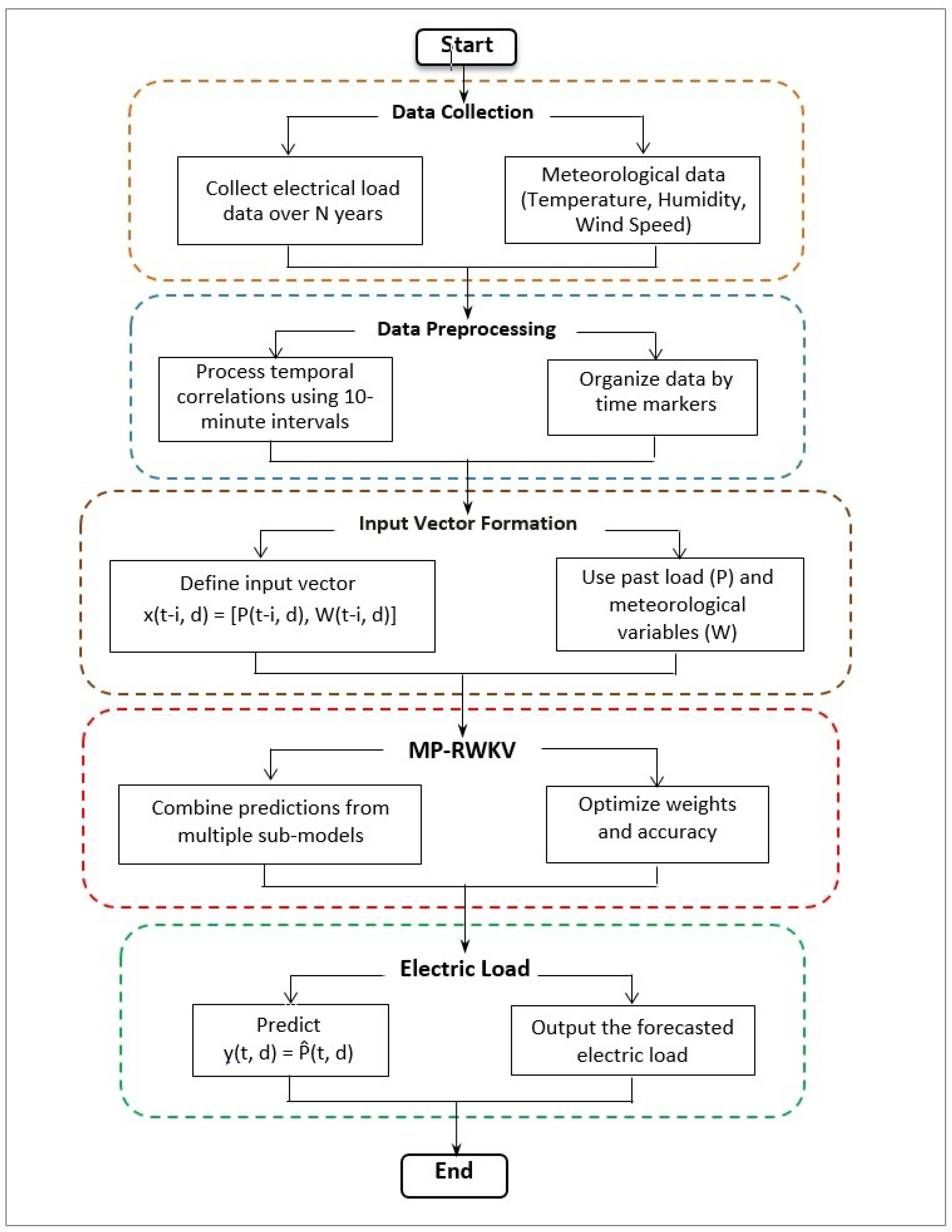
4.1.1. Data Collection

The dataset comprises power consumption measurements from three distinct regions (Quads, Smir, and Boussafou) in the urban power distribution network of Tetouan, Morocco. Data collection was conducted throughout 2017, resulting in 52,416 samples with a granularity of 10-minute intervals.

4.1.2. Feature Composition

Each data point consists of nine features:

Meteorological Variables

• Temperature (${\mathrm{Temp}}_{t,d}\in \mathbb{R}$);
• Relative Humidity (${\mathrm{Hum}}_{t,d}\in \mathbb{R}$);
• Wind Speed (${\mathrm{Ws}}_{t,d}\in \mathbb{R}$).

Temporal Indicators

• Hour of Day ($h\in \{0,1,\dots ,23\}$);
• Day of Week ($d_w\in \{1,2,\dots ,7\}$);
• Month ($m\in \{1,2,\dots ,12\}$).

Power Generation

• Region 1 Power Load ($P_{t,d}^1\in {\mathbb{R}}^{+}$);
• Region 2 Power Load ($P_{t,d}^2\in {\mathbb{R}}^{+}$);
• Region 3 Power Load ($P_{t,d}^3\in {\mathbb{R}}^{+}$) - Target Variable.

4.1.3. Data Characteristics

The dataset exhibits the following properties:

• Temporal coverage: 365 days;
• Sampling frequency: 144 samples per day;
• Total duration: 8736 h;
• Missing values: <0.1%;
• Data range: Normalized to [0,1] for each feature.

Figure 3 presents the statistical characteristics of weather factors and power consumption across the three monitored regions, providing insights into the data distribution and seasonal patterns.

4.2. Baseline Models for Comparison

We evaluate our proposed model against several state-of-the-art architectures specialized in time series forecasting:

Advanced Neural Architectures

• RWKV-TS [15]: The foundation model upon which our enhanced MP-RWKV is built, featuring efficient recurrent computation with the ability to handle long sequences.
• Transformer [16]: The canonical attention-based architecture that revolutionized sequential modeling. Recent studies have demonstrated its effectiveness in Long-Sequence Time Series Forecasting (LSTF).
• Autoformer [17]: A Transformer-based model incorporating decomposition blocks to explicitly model seasonal–temporal patterns, specifically designed for long-horizon forecasting.
• Informer [18]: An enhanced Transformer variant optimized for long-term sequence prediction, featuring improved computational efficiency through sparse attention mechanisms.
• Reformer [19]: A memory-efficient variant utilizing locality-sensitive hashing for attention computation, achieving $\mathcal{O}(LlogL)$ complexity while maintaining comparable performance.
• LSTM [20]: A foundational recurrent architecture that addresses gradient instability through gating mechanisms, enabling effective modeling of long-term dependencies.

4.3. Evaluation Metrics

Model performance is evaluated using two standard metrics: Mean Absolute Error (MAE) and mean-squared error (MSE). Let ${\left\{y_i\right\}}_{i=1}^n$ denote the ground truth values and ${\left\{{\widehat{y}}_i\right\}}_{i=1}^n$ denote the model predictions.

4.3.1. Mean Absolute Error

MAE measures the average magnitude of prediction errors:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|$$

(1)

where n represents the number of prediction points.

4.3.2. Mean-Squared Error

MSE quantifies the average squared deviation of predictions:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2$$

(2)

These metrics provide complementary perspectives on model performance:

• MAE offers an interpretable measure of prediction accuracy in the original scale
• MSE penalizes larger errors more heavily, making it particularly sensitive to outliers

For both metrics, lower values indicate better performance. The statistical significance of performance differences is assessed through paired t-tests with $p<0.05$.

4.4. Short-Term Forecasting Results

Table 2. Performance comparison of different models on short-term power load forecasting (48 h input).

Hours	MP-RWKV-TS		RWKV-TS		Informer		Autoformer		Transformer		Reformer		LSTM
	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
24	0.0552	0.1845	0.0585	0.1902	0.0597	0.1929	0.2464	0.3997	0.1153	0.2943	0.2983	0.4738	0.0787	0.2245
48	0.0798	0.2315	0.0825	0.2378	0.0910	0.2424	1.2121	0.9072	0.1855	0.3766	0.3196	0.4922	0.1057	0.2533
72	0.0812	0.2325	0.0835	0.2378	0.0964	0.2584	0.2771	0.4115	0.1866	0.3779	0.4423	0.5895	0.1299	0.2988
96	0.0998	0.2645	0.1035	0.2705	0.1165	0.2879	0.8902	0.7659	0.2354	0.4396	0.4228	0.5731	0.1233	0.2879
120	0.1025	0.2685	0.1065	0.2755	0.1159	0.2848	0.4739	0.5371	0.2106	0.4043	0.4412	0.5858	0.1372	0.3157

Note: Bold values indicate the best performance for each metric. MSE: mean-squared error; MAE: Mean Absolute Error. Input sequence length is fixed at 48 h for all experiments.

presents the performance comparison of different models on short-term power load forecasting tasks using 48 h of input data to predict power loads at various horizons from 24 h to 120 h.

Figure 4 shows the MAE performance of the selected models using 48 h of data to predict power loads at various horizons. In short-term forecasting scenarios, the MP-RWKV model demonstrates superior performance compared to other models, indicating that preserving past information through context states is crucial for effective prediction. The RWKV-TS model, which also utilizes a similar mechanism, shows comparable performance, highlighting the effectiveness of this approach. Notably, our enhanced MP-RWKV consistently outperforms the base RWKV-TS model, demonstrating the value of parallel processing paths for handling temporal patterns and cross-variable relationships simultaneously.

4.5. Long-Term Forecasting Results

Table 3. Performance comparison of different models on long-term power load forecasting.

Hours	MP-RWKV-TS		RWKV-TS		Informer		Autoformer		Transformer		Reformer		LSTM
	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
144	0.1955	0.3825	0.2015	0.3895	0.2690	0.4561	0.7061	0.6181	0.2692	0.4517	0.8949	0.8672	0.7509	0.7675
192	0.2485	0.4315	0.2568	0.4398	0.2979	0.4813	1.0563	0.7284	0.2736	0.4566	0.8762	0.8449	0.8128	0.8054
240	0.2255	0.4105	0.2335	0.4182	0.2691	0.4542	0.4664	0.5451	0.2510	0.4353	0.8868	0.8447	0.5970	0.6731
288	0.2335	0.4085	0.2415	0.4162	0.2544	0.4305	1.3293	0.7713	0.2111	0.3920	0.9092	0.8578	0.7085	0.7285
432	0.1895	0.3625	0.1965	0.3705	0.2786	0.4440	0.4519	0.5148	0.2357	0.4173	0.9253	0.8592	0.7808	0.7629

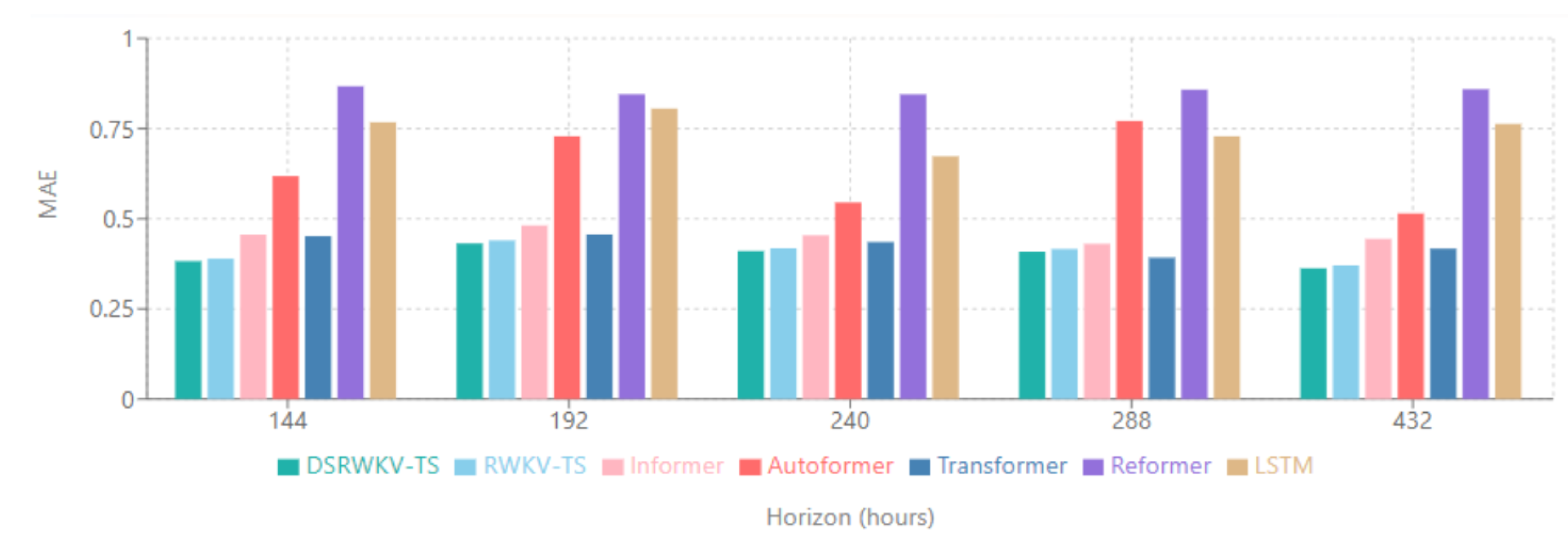
Note: Bold values indicate the best performance for each metric. MSE: mean-squared error; MAE: Mean Absolute Error. Input sequence length is fixed at 8 h for all experiments.

presents the performance comparison for long-term forecasting scenarios, where models use 8 h of input data to predict power loads at extended horizons from 144 h to 432 h.

Figure 5 presents the long-term forecasting results showing MAE performance when using 8 h of data to predict power loads at horizons ranging from 144 h to 432 h. In these extended prediction scenarios, traditional Transformer-based models (Informer, Autoformer, and Reformer) show significant performance deterioration as the prediction horizon increases. The MP-RWKV model maintains consistent performance even over extended forecasting periods, demonstrating its robustness through parallel processing paths, adaptive fusion mechanisms, and position-aware attention that effectively capture both short-term patterns and long-term dependencies.

The experimental results demonstrate that MP-RWKV consistently outperforms the base RWKV-TS model across all long-term forecasting horizons, with the performance gap increasing at more extended prediction ranges. This indicates that the parallel pathway processing and adaptive integration of temporal and cross-variable information become increasingly beneficial as the forecasting horizon extends. While the base LSTM model shows declining accuracy as the prediction horizon increases due to gradient vanishing issues, the MP-RWKV model maintains stable performance across all tested scenarios.

5. Conclusions

This paper introduces MP-RWKV, an enhanced model that builds upon RWKV-TS to address the limitations of existing approaches in time series forecasting, particularly for power load prediction. Through our comprehensive experimental analysis, we demonstrate that MP-RWKV consistently outperforms other state-of-the-art models across both short-term and long-term forecasting horizons.

The experimental results show that MP-RWKV achieves superior performance in short-term forecasting scenarios, effectively capturing temporal patterns through its context state mechanism. In long-term forecasting, while traditional models like LSTM suffer from gradient vanishing and Transformer-based models show deteriorating performance, MP-RWKV maintains consistent accuracy even at extended prediction horizons, demonstrating its robust handling of temporal dependencies.

The key findings from our experiments include

• MP-RWKV demonstrates consistently lower MAE values compared to baseline models, including its predecessor RWKV-TS
• The model maintains stable performance across different prediction horizons, from 24 h to 432 h
• The parallel processing path approach effectively balances short-term pattern recognition with long-term dependency modeling
• The adaptive fusion mechanism successfully integrates temporal and cross-variable information, leading to more robust predictions

Future research directions include

• Extending the model to handle multi-variable forecasting scenarios with even more diverse data sources
• Incorporating additional parallel processing paths for specialized handling of different data characteristics
• Exploring applications in other domains requiring time series forecasting
• Optimizing computational efficiency for real-world deployments

In conclusion, MP-RWKV represents a significant advancement in power load forecasting, building upon and enhancing the capabilities of RWKV-TS. Its consistent performance and versatility make it a promising solution for power system operations and planning, contributing to the development of more efficient and reliable smart grid technologies.