Tuning and Performance Analysis of Second-Order Linear Active Disturbance Rejection Controller for Trajectory Tracking and Balancing the Rotary Inverted Pendulum †
Abstract
1. Introduction
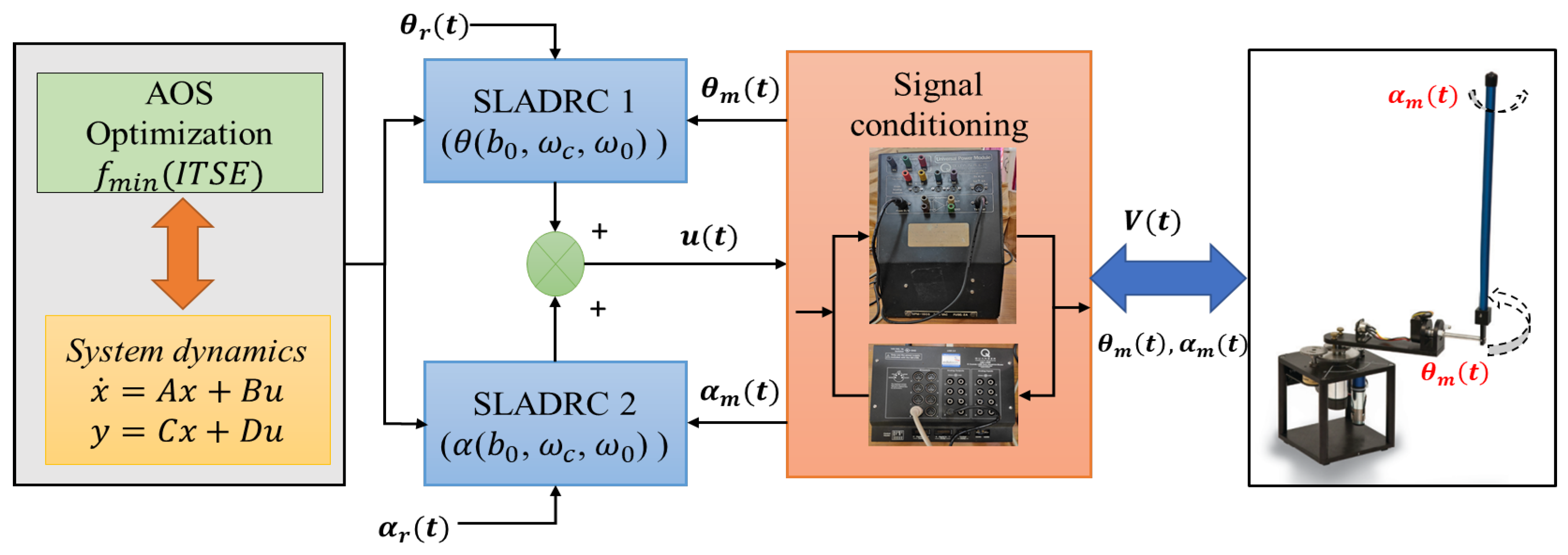
2. Problem Description
2.1. Mathematical Modeling of the RIP
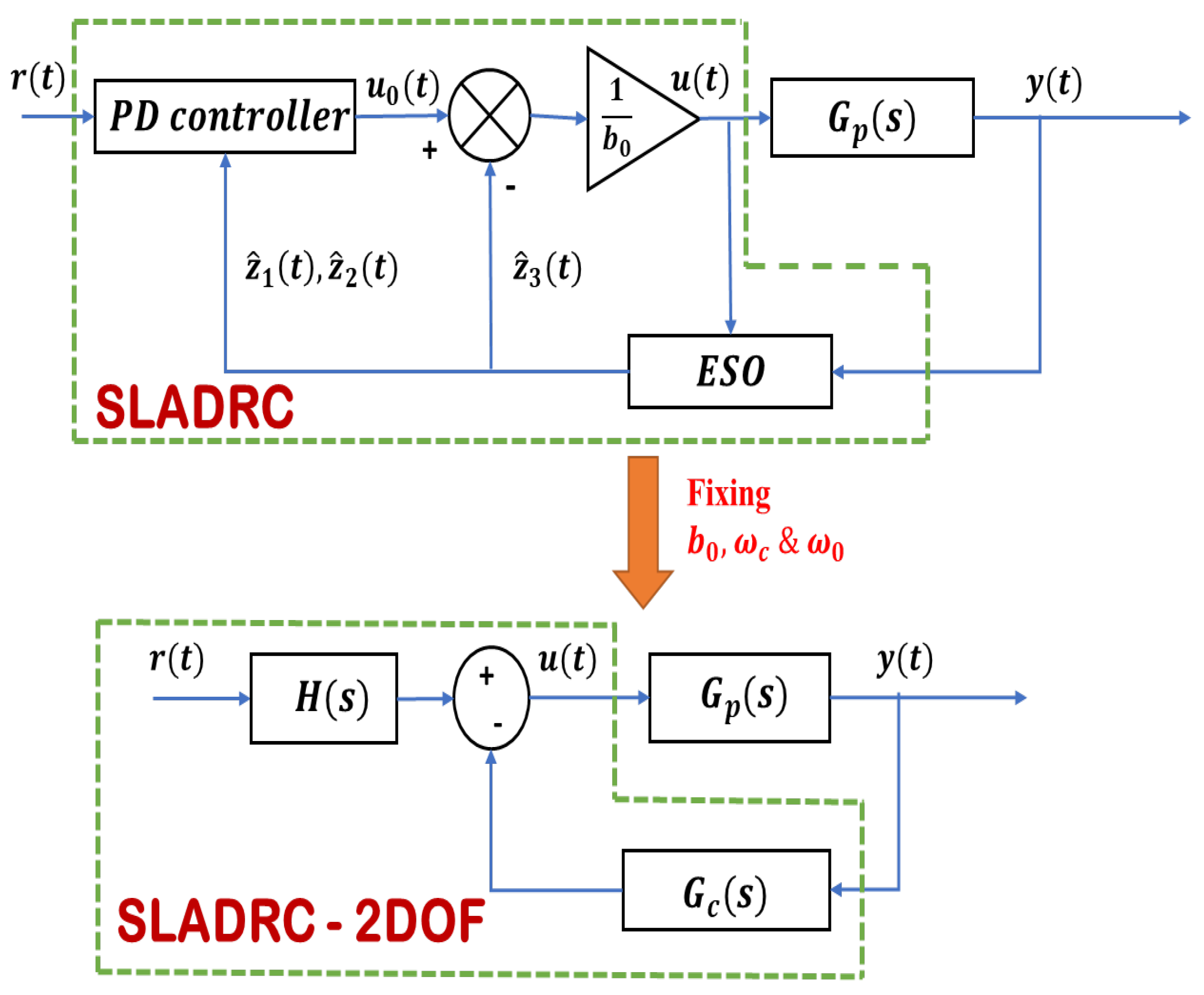
2.2. SLADRC Preliminaries
3. Atomic Orbital Search Optimization
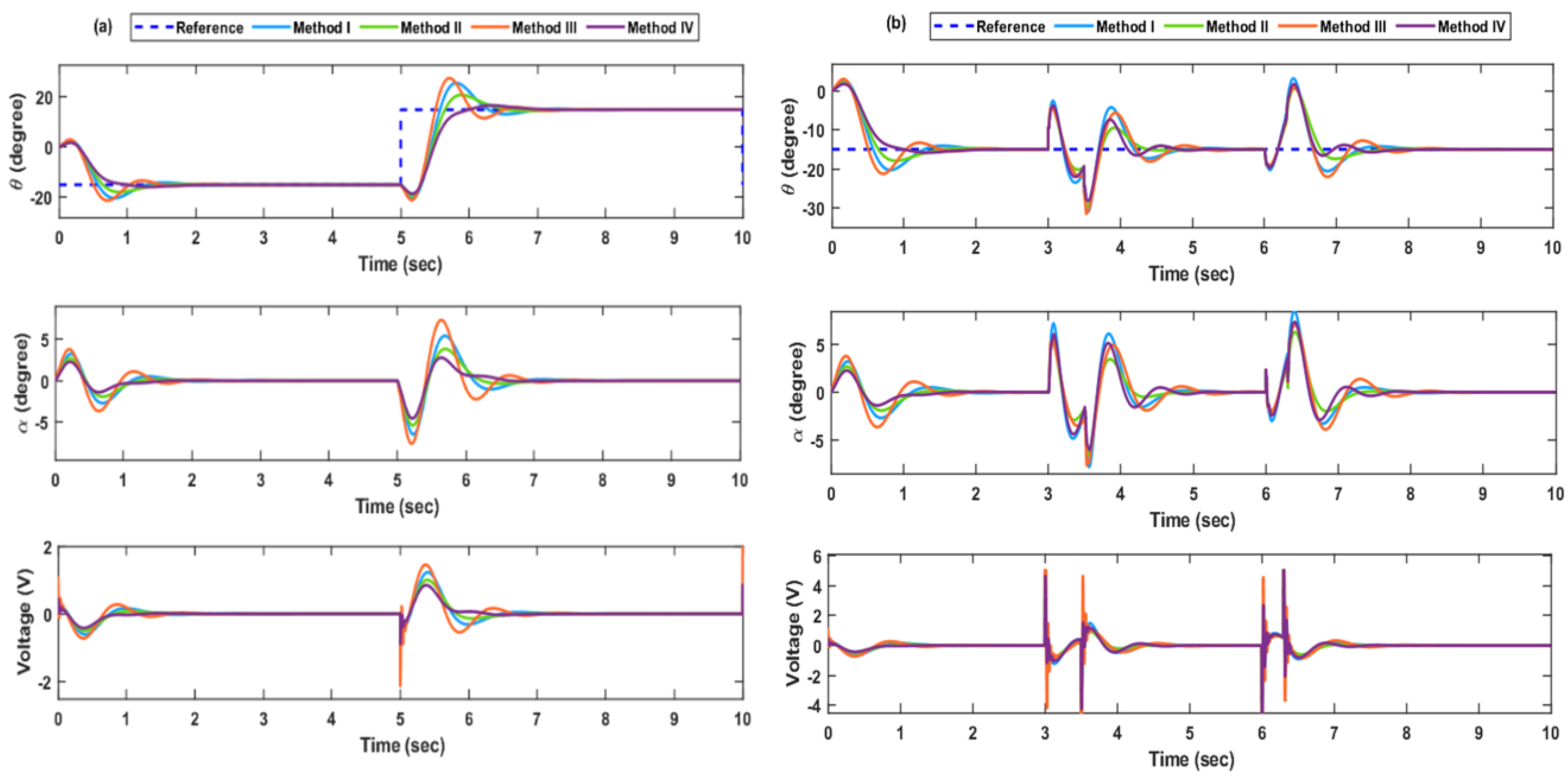
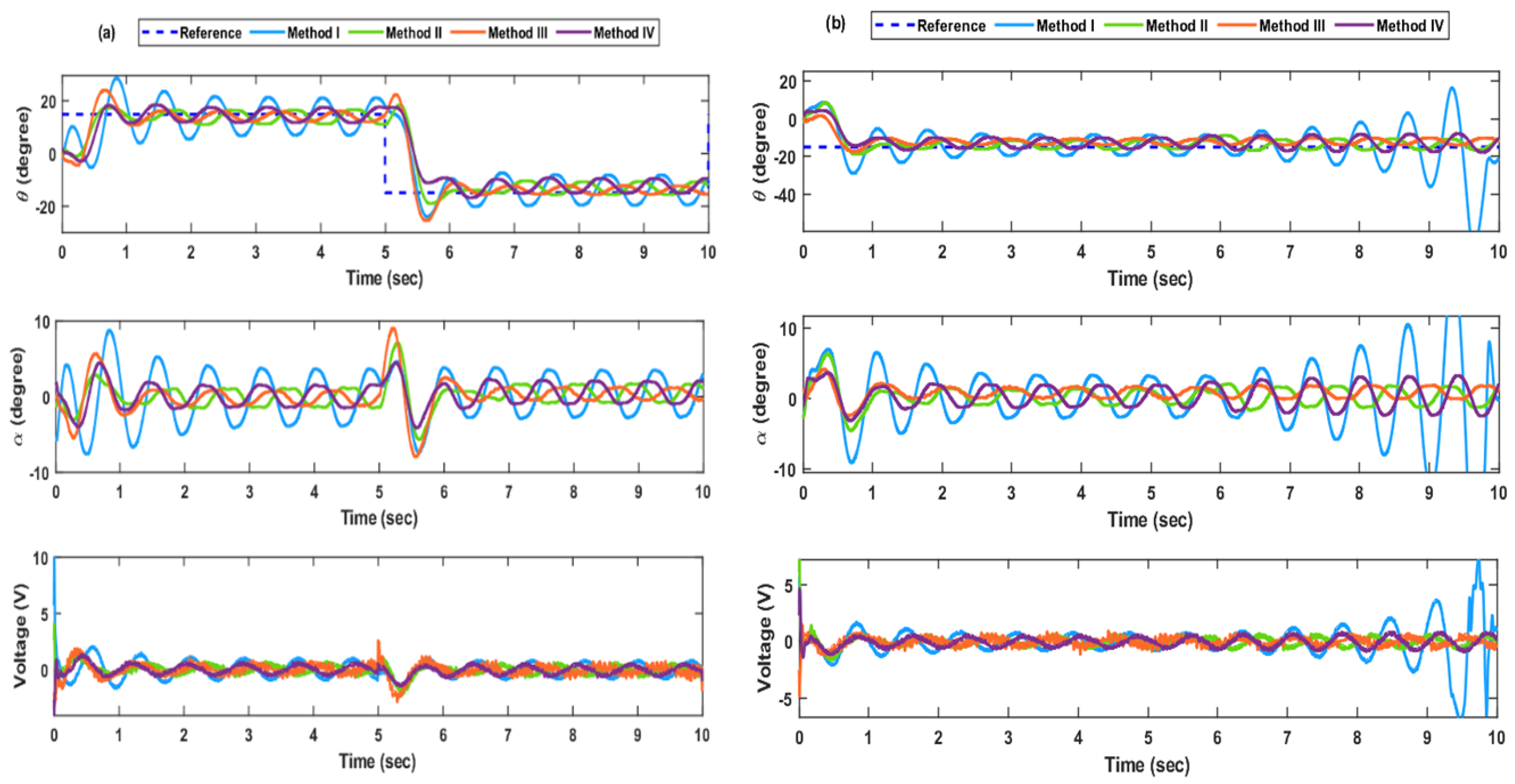
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adharsh Lal, M.; Kunjumuhammed, A.; Tomy, J.; Urmila, G.; Sivadas, M.; Mohan, A. Stabilization of Rotary Inverted Pendulum using PID Controller. In Proceedings of the 2021 8th International Conference on Smart Computing and Communications: Artificial Intelligence, AI Driven Applications for a Smart World, ICSCC 2021, Kochi, India, 1–3 July 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 376–380. [Google Scholar]
- Dwivedi, P.; Pandey, S.; Junghare, A.S. Robust and novel two degree of freedom fractional controller based on two-loop topology for inverted pendulum. ISA Trans. 2018, 75, 189–206. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, A.; Victoire, A.A. Optimization Reinforced PID-Sliding Mode Controller for Rotary Inverted Pendulum. IEEE Access 2023, 11, 24420–24430. [Google Scholar] [CrossRef]
- Fatihu Hamza, M.; Jen Yap, H.; Ahmed Choudhury, I. Cuckoo search algorithm based design of interval Type-2 Fuzzy PID Controller for Furuta pendulum system. Eng. Appl. Artif. Intell. 2017, 62, 134–151. [Google Scholar] [CrossRef]
- Pan, J.; Qi, S.; Wang, Y. Flatness based active disturbance rejection control for cart inverted pendulum and experimental study. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015; pp. 4868–4873. [Google Scholar]
- Ramírez-Neria, M.; Sira-Ramírez, H.; Garrido-Moctezuma, R.; Luviano-Juarez, A. On the linear active disturbance rejection control of the Furuta pendulum. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014; pp. 317–322. [Google Scholar]
- Liu, B.; Hong, J.; Wang, L. Linear inverted pendulum control based on improved ADRC. In Systems Science and Control Engineering; Taylor and Francis Ltd.: Abingdon, UK, 2019; Volume 7, pp. 1–12. [Google Scholar]
- Chen, Q.; Zhuang, J.; Liu, B.; Yang, P. Inverted Pendulum Balance Control Based on Improved Active Disturbance Rejection Control. In Proceedings of the 2022 Chinese Automation Congress, CAC 2022, Xiamen, China, 25–27 November 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022; pp. 1526–1531. [Google Scholar]
- Herbst, G. A simulative study on active disturbance rejection control (ADRC) as a control tool for practitioners. Electronics 2013, 2, 246–279. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Kumar, R.; Bothara, Y.; Ezhilarasi, D.; Mohanavelu, K. Atomic Orbital Search Optimization Based Fractional Order PID Controller for 4 DoF Lower Limb Exoskeleton. In Proceedings of the 2023 International Conference on Power, Instrumentation, Control and Computing, PICC 2023, Thrissur, India, 19–21 April 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar]
- Quanser, Rotary Inverted Pendulum Manual. Available online: https://www.made-for-science.com/de/quanser/?df=made-for-science-quanser-rotary-double-inverted-pendulum-coursewarestud-matlab.pdf (accessed on 1 September 2024).
- Hao, Z.; Yang, Y.; Gong, Y.; Hao, Z.; Zhang, C.; Song, H.; Zhang, J. Linear/Nonlinear Active Disturbance Rejection Switching Control for Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 9334–9347. [Google Scholar] [CrossRef]
- Dai, X.; Zhao, C.; Xu, R. Nonlinear Active Disturbance Rejection Control for Vehicle Active Suspension System. In Proceedings of the 2023 3rd International Conference on Electronic Information Engineering and Computer Science, EIECS 2023, Changchun, China, 22–24 September 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023; pp. 633–637. [Google Scholar]
- Wang, Y.; Tan, W.; Cui, W.; Han, W.; Guo, Q. Linear active disturbance rejection control for oscillatory systems with large time-delays. J. Franklin Inst. 2021, 358, 6240–6260. [Google Scholar] [CrossRef]


| Methods/(Number of Tuning Parameters) | Tuning Parameters | Approximations | Reference |
|---|---|---|---|
| I/(8) | None | [13] | |
| II/(5) | , | [14] | |
| III/(4) | Fixing . | [15] | |
| IV/(2) | Fixing the . ( for RIP) | [9] |
| RIP Parameters | AOS Optimization | Optimization Search Bounds | ||||
|---|---|---|---|---|---|---|
| Symbols | Description | Values/Units | Parameters | Values | Parameters | Bounds |
| Mass of Pendulum | 0.127 | Energy Update Coefficient | 0.5 | [−20, −1] | ||
| Total length of Pendulum | 0.337 | Orbital Radius | 0.5 | [1, 20] | ||
| Rotary arm length from pivot to tip | 0.2159 | Energy Decay Factor | 0.95 | , | [30, 60], [70, 100] | |
| Pendulum viscous damping coefficient | 0.0024 | Number of iterations | 30 | , | [10, 20], [50, 70] | |
| Motor arm moment of inertia | 9.9824 | Number of populations | 50 | [1, 20] | ||
| Gravitational constant | 9.81 | Weighting Factor for global search | 0.5 | [5, 20] | ||
| Tuning Methods | Optimized Parameter Values | Computation Time (s) | |||||
|---|---|---|---|---|---|---|---|
| I | = −13.10, = 51.39, = 15.99, = 5.527 = 18.820, = 79.68, = 56.92, = 16.5822 | [6.75°, 23.5°] | 16.75° | [−4.2°, 4.05°] | 8.25° | 3.632 × 10−5 | 1276 |
| II | = −15.492, = 4.984, = 19.638, = 9.155, k = 11.70 | [12.7°, 16.5°] | 3.8° | [−1.5°, 1.5°] | 3° | 1.51632 × 10−4 | 835 |
| III | = −9.395, = 6.165, = 8.759, = 8.9517 | [12.2°, 16.2°] | 4° | [−1.2°, 1.2°] | 2.4° | 2.12632 × 10−4 | 412 |
| IV | = −9.465, = 13.889 | [11.9°, 17.6°] | 5.7° | [−1.5°, 1.5°] | 3° | 3.94632 × 10−4 | 396 |
| Tuning Methods | I | II | III | IV | |||||
|---|---|---|---|---|---|---|---|---|---|
| Performance | Parameters | Sim | Exp | Sim | Exp | Sim | Exp | Sim | Exp |
| Time Domain performance | Ts/s () | 2 | 2 | 1.5 | 1.5 | 1.5 | 1.5 | 1 | 1.2 |
| Ts/s () | 2 | 2.5 | 1.25 | 1.5 | 1.5 | 1.5 | 1 | 1.5 | |
| Mp/% | 73 | 53 | 33 | 27 | 40 | 38 | 10 | 8 | |
| Us/% | 33 | 0 | 27 | 33 | 46 | 35 | 20 | 0 | |
| Servo (Set point tracking) | TV | 0.6391 | 0.6673 | 0.839 | 0.822 | 2.118 | 1.834 | 0.885 | 0.945 |
| ITSE () | 2.742 | 6931 | 2.742 | 1.09 × 103 | 2.741 | 1.40 × 103 | 2.742 | 1.04 × 103 | |
| ITSE () | 4.30 × 10−11 | 214.2 | 2.86 × 10−14 | 14.02 | 1.51 × 10−10 | 4.171 | 1.03 × 10−11 | 33.49 | |
| Regulatory () | TV | 2.87 × 10−5 | 8.17 × 10−3 | 8.39 × 10−6 | 0.0479 | 1.25 × 10−4 | 0.055 | 5.43 × 10−6 | 0.0201 |
| ITSE () | 2.77 × 10−8 | 8594 | 4.69 × 10−9 | 231.2 | 1.68 × 10−10 | 164.4 | 9.96 × 10−11 | 359 | |
| ITSE () | 1.69 × 10−9 | 3796 | 2.21 × 10−10 | 41.83 | 1.55 × 10−9 | 16.69 | 5.85 × 10−11 | 66.74 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekaran, J.; Deenadayalan, E. Tuning and Performance Analysis of Second-Order Linear Active Disturbance Rejection Controller for Trajectory Tracking and Balancing the Rotary Inverted Pendulum. Eng. Proc. 2025, 95, 2. https://doi.org/10.3390/engproc2025095002
Gunasekaran J, Deenadayalan E. Tuning and Performance Analysis of Second-Order Linear Active Disturbance Rejection Controller for Trajectory Tracking and Balancing the Rotary Inverted Pendulum. Engineering Proceedings. 2025; 95(1):2. https://doi.org/10.3390/engproc2025095002
Chicago/Turabian StyleGunasekaran, Janeshwaran, and Ezhilarasi Deenadayalan. 2025. "Tuning and Performance Analysis of Second-Order Linear Active Disturbance Rejection Controller for Trajectory Tracking and Balancing the Rotary Inverted Pendulum" Engineering Proceedings 95, no. 1: 2. https://doi.org/10.3390/engproc2025095002
APA StyleGunasekaran, J., & Deenadayalan, E. (2025). Tuning and Performance Analysis of Second-Order Linear Active Disturbance Rejection Controller for Trajectory Tracking and Balancing the Rotary Inverted Pendulum. Engineering Proceedings, 95(1), 2. https://doi.org/10.3390/engproc2025095002






