Abstract
Robust robot manipulation hinges on effective state estimation. The VRT 6 robot leverages an inertia measurement unit with triaxial gyroscopes, magnetometers, and accelerometers, as well as a position sensor, but these sensors are plagued by noise that demands rigorous filtering. To tackle this, an adaptively scaled unscented Kalman filter was employed. The filter’s scaling parameter was meticulously optimized using density- and moment-based techniques, as both system properties and estimated state impact this crucial parameter. A Maximum Likelihood Estimation (ML) substantiates the enhanced quality of the estimated velocity and acceleration, on par with the position estimate. Minimizing measurement prediction error (MMPE) also shows better results with less RMSE when compared to fixed-kappa values, and the quality of position estimates is higher with the increase in the domain of the scaling parameter. By carefully selecting the adaptive scaling parameters’ range to minimize sigma point weights and ensure the positive definiteness of the covariance matrix, this enhanced UKF method achieved markedly superior state estimates compared to standard UKF implementations.
1. Introduction
The accuracy of industrial robots is a crucial requirement for their use. Robot positioning capabilities have been improved by successful calibration procedures rather than hardware modifications [1,2,3]. Among the existing robot calibration methods, an inertial sensor is one of the best choices to automatically obtain an online calibration. It also has drawbacks like other measurement techniques and can be addressed using sensor calibration [4]. The extended Kalman filter and unscented Kalman filter are widely regarded as the most effective techniques for combining data from an inertial measurement unit and a position sensor [5,6]. Effective state estimation requires a suitable model that can capture the system’s dynamic behavior and characterize the noise properties, which are often not well understood in practical real-world scenarios [7]. Conventional local techniques utilize low-order Taylor series approximations to represent nonlinear functions. Taylor linearization can lead to inaccuracy and bias and may encounter convergence issues due to rough approximations. This leads to the design of local filters based on polynomial interpolation or unscented transformation [8]. Polynomial interpolation provides a powerful means of approximating nonlinear functions by leveraging their means and covariance matrices, making it a highly effective technique. A strategically chosen set of points is also employed to accurately estimate the system state, which is often called the unscented transformation (UT). This type of local filter is often referred to as an unscented Kalman filter (UKF) due to the fact that it does not contain any derivatives. [9,10]. The scaling parameter determines the computation of the measurement prediction in UKF. Derivative-free filters are designed using scaling parameters that shape the quality of the approximation and, consequently, the quality of state estimates [11,12]. In general, the choice of scaling parameters is independent of the description of the system but depends on the order of the system only. There is a problem with positive definiteness in the standard scaling parameter in a UT when applied to higher-order systems. Researchers have largely avoided considering a suitable scaling parameter in their studies. As a result, only a few general suggestions have been made, which do not respect the specific description of the system. Therefore, the user has a greater degree of control over the parameter. The scaling parameters in this filter are thus determined by using an adaptive technique based on density and moment criteria. In density-based criteria, a choice is based on evaluating the scaling parameters to maximize their likelihood utilizing measurement information. In moment-based criteria, a choice is based on finding the scaling parameters by minimizing the measurement prediction error. A simplified adaptation procedure is applied to analyze all criteria in the state estimation of the VRT 6 robot.
2. Kinematic Model of the Robot
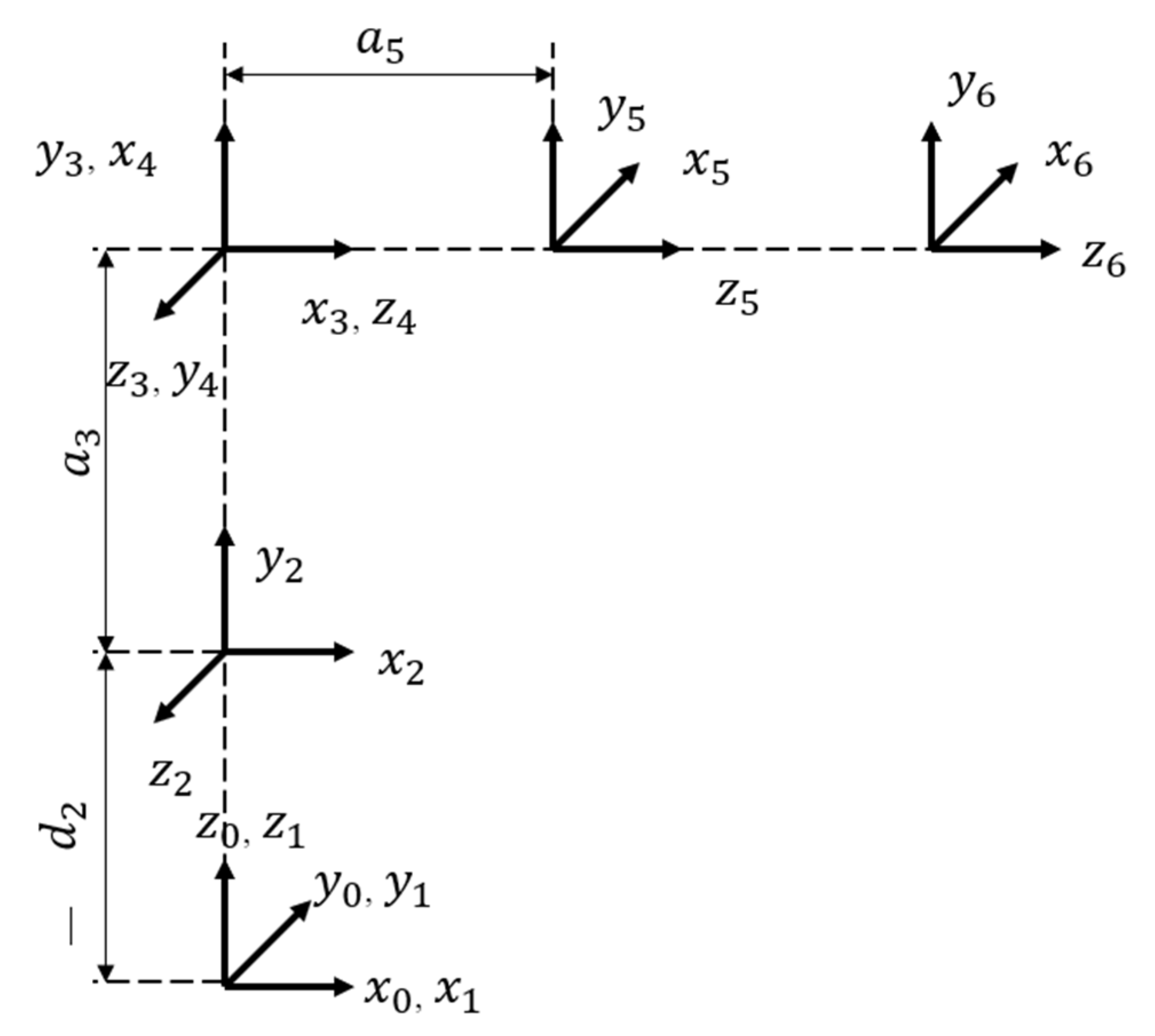
The VRT 6 robot can handle a substantial 2 kg load with ease. Its articulated design endows it with exceptional dexterity, allowing it to seamlessly navigate through five distinct axes of motion. The robot is also equipped with a sophisticated pneumatic gripper, granting it remarkable grasping capabilities. The kinematics of these robotic manipulators are modeled using the Denavit–Hartenberg convention, where the transformation between neighboring link coordinate frames can be represented by a homogeneous matrix that depends on various parameters such as joint angle, link offset, link twist, and link length. A set of possible body-fixed coordinate frames is shown in Figure 1. Kinematic analysis relies on rigidly attaching coordinate frames to each link in order to understand and describe the motion of robotic manipulators and articulated robots. The kinematic parameters detailed in the DH model are provided in Table 1.
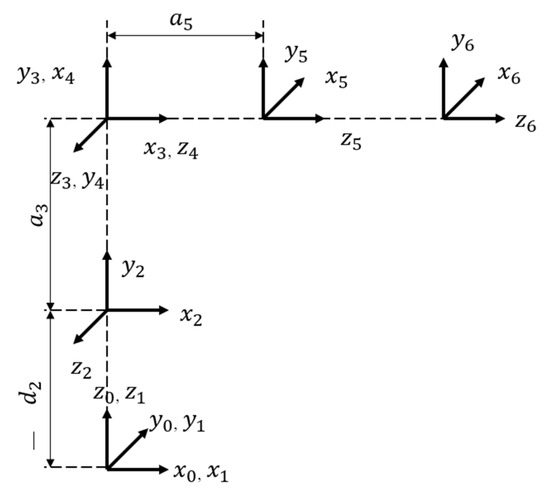
Figure 1.
Coordinate frame of the VRT 6 robot.

Table 1.
Joint space parameters for 6 DOFs.
3. Unscented Kalman Filter
An advancement in state estimation could be made with the unscented Kalman filter. It provides real-time, recursive state estimates that are continuously updated as new sensor data arrive, and it integrates noisy, high-frequency IMU data with noisy, low-frequency position sensor data to estimate the state accurately. It also corrects IMU drift by using position sensor data and maintains an accurate position estimation and orientation. The UKF generates a series of strategically placed sampling points around the covariance of the current state estimates, enabling more accurate and robust state inference. Propagating the sigma points through the nonlinear mapping enables an accurate estimation of the mean and covariance [13]. The propagation of points through the nonlinear system is drastically streamlined, decreasing from 2 (L + q) to just 2 L, where L corresponds to the state vector’s length. The sigma points (χ) and corresponding weights ( are as follows:
Cholesky decomposition calculates the lower triangular matrix similarly to [14]. In addition to generating the sigma points, the nonlinear function propagates them. The sigma point’s value is predicted based on the previous step’s information.
The mean and covariance are calculated by averaging the transformed sigma points using the given weight values.
By assuming additive noise, it is vital to incorporate the process noise covariance matrix, Q, into the error covariance matrix. This crucial adjustment enables the transformed sigma points to be reliably propagated through the observation function, yielding robust and accurate results.
These derived sigma points, , are then strategically employed to rigorously compute the average measurement, the comprehensive covariance matrix describing the measurement, and the pivotal cross-covariance linking the state and measurement.
In order to capture the additive noise assumption, we augment the output covariance matrix with the measurement noise covariance matrix R. The Kalman gain matrix is estimated from the cross-correlation and measurement covariances.
The updated measurement equations are
3.1. Tuning Kappa
The optimal value is calculated as [15] where represents the number of dimensions in the state space. This value experiences a loss of positive definiteness as the state dimension increases ( then is assumed to be zero for any results in the cubature Kalman filter [15]. Standard methods often rely on system order without accounting for system description, leading to subjective parameter adjustments that may not fully optimize estimation quality. A more constructive approach is to replace standard parameter choices with an adaptive scaling parameter, using density- and moment-based criteria to objectively improve the estimation process.
- 1.
- Density-based criteria: Maximum Likelihood Estimation (ML)
- 2.
- Moment-based criteria: minimizing measurement prediction error (MMPE)
3.2. Adaptation Parameters in UKF
This algorithm offers a compelling alternative that can be summarized as follows:
- Step 1: The initial conditions prior to the estimations and are established. A set of criteria for dynamically and adaptively choosing the appropriate value is developed in order to optimize the performance and robustness of the filter.
- Step 2: The optimal is computed for the chosen criterion. The optimal scaling parameter in the maximum likelihood criteria was computed by the grid point method as . was chosen in such a way that its upper limit is . The central sigma point weight is and . To ensure a reliable and stable estimation procedure, the calculated covariance matrices were guaranteed with > 0.
- Step 3: and can be found as in Equations (7) and (8) for the chosen criterion and its optimal scaling parameter.
- Step 4: and can be obtained as in Equations (14) and (15) for the chosen criterion and its optimal scaling parameter.
4. Experiment
A VRT 6 robot was employed in this study to robustly validate the proposed hybrid system comprising a single IMU and a position sensor, as depicted in Figure 2. The position sensor was strategically integrated at the core of the IMU. This IMU was equipped with three-axis accelerometers, magnetometers, and gyroscopes. The gyroscope provides a wide selection of full-scale ranges, spanning from 250 degrees per second up to 2000 degrees per second. Similarly, the accelerometer offers a variety of measurable ranges, from 2 g to 8 g. Both sensors output 16-bit data per axis. The magnetometer is a 3-axis Hall-effect sensor with a ± 4800 µT range. Both the position sensor and IMU were sampled at 100 Hz.

Figure 2.
Hybrid calibration system.
The sensor module was aligned with the north–east–down (NED) directions, as in [13], and considered as the zero-point reference. The robot’s configuration was changed by selecting an arbitrary home position and then incrementally adjusting the home joint angles. The serial data communication system was configured to seamlessly integrate the robot and PC into a comprehensive measurement system. Once the robot reaches a designated position, its controller signals the sensor to commence the measurement process. Upon completion of the measurement, the robot then transitions to the next position, and this iterative procedure continues until the full measurement task is satisfactorily executed. The sensors’ output is fed into the UKF algorithm. This approach was evaluated by measuring 100 poses to verify the proposed algorithm’s effectiveness.
5. Results and Discussion
The state is estimated using a UKF with , , and [11]. The grid-based maximization procedure is utilized at each time step to optimize the likelihood function (16) across the range defined by the parameters , and . The filter performance for the position estimate of 100 poses is measured by their mean-squared errors and is summarized in Table 2. When the tuning parameter kappa is set to , the position estimation accuracy shows a notable improvement of 40% for the Maximum Likelihood Estimate method. In contrast, the improvement for the minimizing measurement prediction error estimation method is comparatively lower at 15%. The estimation accuracy is enhanced by 55% and 30% with MLE and MMPE, respectively, for . With ), the position estimate accuracy was nearly 60% across both cases, indicating the proposed method’s effectiveness in integrating the IMU and position sensor data. These results also indicate that the adaptive scaling parameter outperforms the standard kappa value. It maximizes the likelihood that it can significantly improve the estimation quality, leading to a lower root-mean-square error. The MMPE criteria also show better results with fewer RMSEs when compared to fixed kappa values.

Table 2.
Average RMSE of the position estimate of UKF under different choices of scaling parameters.
The quality of the position estimate is higher with the increase in the domain of the scaling parameter , as in [12], in both criteria. has been shown to generate more accurate estimates compared to other variants. Similarly, the filter performance of velocity (RMSE)V and acceleration (RMSE)A estimates is calculated by their mean-squared errors and is presented in Table 3. The velocity estimate was considerably enhanced, demonstrating a remarkable improvement of nearly 65%, which was accomplished through a strategic expansion of the scaling parameter range. Furthermore, the accuracy of the acceleration estimation also underwent a substantial increase of 60%, as evidenced under the rigorous scrutiny of both the MLE and MMPE analytical approaches.

Table 3.
Average RMSE of velocity and acceleration estimates of UKF under different scaling parameters.
Utilizing a variable scaling parameter, rather than a fixed value, yields markedly improved estimates of velocity and acceleration in comparison to standard approaches [14]. The Maximum Likelihood Estimation criterion substantiates the enhanced quality of the estimated velocity and acceleration, which is on par with the position estimates. Notably, the step size has a negligible impact on the improvement in estimation quality, which remains consistent across the full range of the scaling parameters. Expanding the scaling parameters’ range has enhanced the accuracy of the position estimates [15]. The unscented Kalman filter’s performance will be rigorously examined by considering diverse scaling parameter settings, as quantified by the average filtering covariance matrix.
Here, is the covariance matrix determinant for n poses. Table 4 displays the average filtering covariance of the state estimate of the VRT 6 robot using a UKF with different domains of the scaling parameter and for different criteria. It projects the overall performance of the filter. The criterion ML and MMPE show the best values in both MSE and VAR for the state estimation of the VRT 6 robot when compared to the UKF with the standard choice of scaling parameters. An adaptive scaling parameter in the UKF allows it to be more flexible and responsive in dynamic and rapidly changing systems [16]. Despite the increase in covariance, this allows better estimations of robot position, velocity, and acceleration in environments that are unpredictable or change quickly.

Table 4.
Average filtering covariance.
6. Conclusions
The unscented Kalman filter technique was explored to estimate the state of VRT 6, with a particular emphasis on selecting the appropriate scaling parameter. The analysis highlighted the limitations of the standard scaling parameter and demonstrated that the adaptive parameter significantly outperformed the fixed version in estimating the state of VRT 6. The estimation performance varies in magnitude for different parameter choices. A Maximum Likelihood Estimation (ML) enhances the accuracy of the state estimation by maximizing the likelihood that the measured data will accurately match the predicted state, while minimizing measurement prediction error (MMPE) criteria does not directly model the likelihood of the data but rather seeks to minimize the discrepancy between the prediction and the actual measurements. The estimated quality is measured by RMSE and average filter covariance. As a result of these measures, it is possible to compare different scaling approaches on the basis of the accuracy and uncertainty of state estimates. Dynamically adjusting the scaling parameter by optimizing the likelihood function yields substantial enhancements in estimation accuracy, as evidenced by the reduced root-mean-square error. Furthermore, marginally expanding the scaling parameter domain also yields enhanced results. The moment-based criterion MMPE also shows a better quality in state estimation when compared to fixed-parameter UKFs. The choice does not rely on the hands of the users. It depends purely on the description of the state and order of the system. This study demonstrates that dynamically adjusting the scaling parameter based on the system’s behavior improves estimation performance and adds more flexibility for robot applications.
Author Contributions
All authors contributed to the study conception and design. Material preparation, data collection, and analysis were carried out by G.S., S.B., V.K.K., and B.T. The first draft of the manuscript was written by G.S., and all authors commented on previous versions of the manuscript. Review and editing were carried out by G.S. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the associated data are included in the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tang, G.; Liu, L. Robot calibration using a single laser displacement meter. Mechatronics 1993, 3, 503–516. [Google Scholar] [CrossRef]
- Lou, Q.; Gonzalez, F.; Kovecses, J. Kinematic Modeling and State Estimation of Exploration Rovers. IEEE Robot. Autom. Lett. 2019, 4, 1311–1318. [Google Scholar] [CrossRef]
- Smith, G.C.; Smith, R.A. A non-contact method for detecting on-line industrial robot position errors using a microwave Doppler radar motion detector. Int. J. Adv. Manuf. Technol. 2005, 29, 605–615. [Google Scholar] [CrossRef]
- Beravs, T.; Podobnik, J.; Munih, M. Three-Axial Accelerometer Calibration Using Kalman Filter Covariance Matrix for Online Estimation of Optimal Sensor Orientation. IEEE Trans. Instrum. Meas. 2012, 61, 2501–2511. [Google Scholar] [CrossRef]
- Won, S.P.; Melek, W.W.; Golnaraghi, F. A Kalman/Particle Filter-Based Position and Orientation Estimation Method Using a Position Sensor/Inertial Measurement Unit Hybrid System. IEEE Trans. Ind. Electron. 2010, 57, 1787–1798. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P. Online Serial Manipulator Calibration Based on Multisensory Process Via Extended Kalman and Particle Filters. IEEE Trans. Ind. Electron. 2014, 61, 6852–6859. [Google Scholar] [CrossRef]
- Hartley, R.; Ghaffari, M.; Eustice, R.M.; Grizzle, J.W. Contact-aided invariant extended Kalman filtering for robot state estimation. Int. J. Robot. Res. 2020, 39, 402–430. [Google Scholar] [CrossRef]
- Šimandl, M.; Duník, J. Derivative-free estimation methods: New results and performance analysis. Automatica 2009, 45, 1749–1757. [Google Scholar] [CrossRef]
- Dunik, J.; Simandl, M.; Straka, O.; Kral, L. Performance analysis of derivative-free filters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 1941–1946. [Google Scholar] [CrossRef]
- Wan, E.A.; van der Merwe, R. The Unscented Kalman Filter. In Kalman Filtering and Neural Networks; ch. 7; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Duník, J.; Šimandl, M.; Straka, O. Adaptive choice of scaling parameter in derivative-free local filters. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Straka, O.; Duník, J.; imandl, M. Unscented Kalman Filter with Advanced Adaptation of Scaling Parameter. Automatica 2014, 50, 2657–2664. [Google Scholar] [CrossRef]
- Dunik, J.; Simandl, M.; Straka, O. Unscented Kalman Filter: Aspects and Adaptive Setting of Scaling Parameter. IEEE Trans. Autom. Control 2012, 57, 2411–2416. [Google Scholar] [CrossRef]
- Rhudy, M.; Gu, Y.; Gross, J.; Napolitano, M.R. Evaluation of Matrix Square Root Operations for UKF within a UAV GPS/INS Sensor Fusion Application. Int. J. Navig. Obs. 2011, 2011, 416828. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-White, H.F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J.; Rizos, C.; Kinlyside, D. Improving Adaptive Kalman Estimation in GPS/INS Integration. J. Navig. 2007, 60, 517–529. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).