Sensitivity Analysis of an Edge-Fed Microstrip Patch Antenna Strain Sensor to Detect Surface Strains †
Abstract
1. Introduction
2. Antenna Design and Parameters
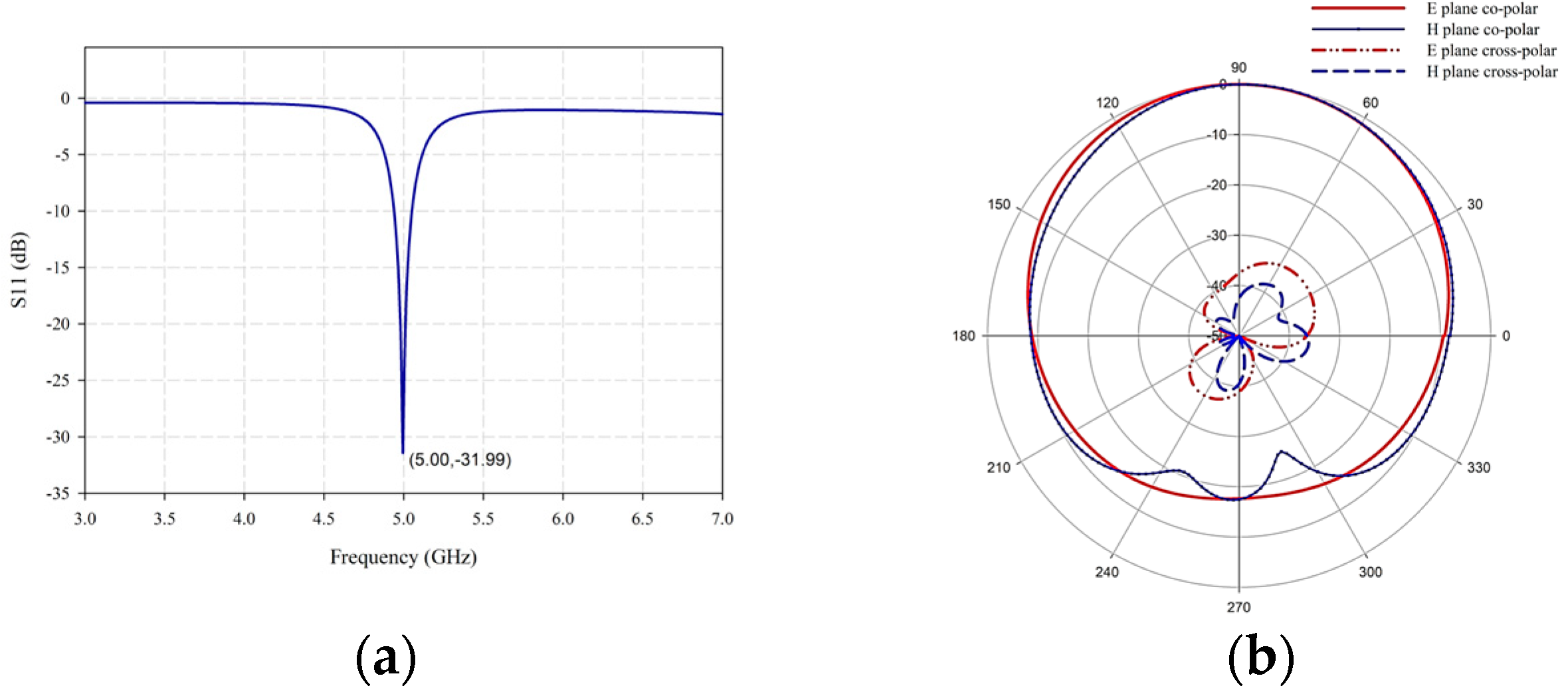
Design of an Edge-Fed Microstrip Antenna
3. Principle of Operation
Antenna Under Tensile Load
4. Simulation of Tensile Test in HFSS
5. Results and Discussion
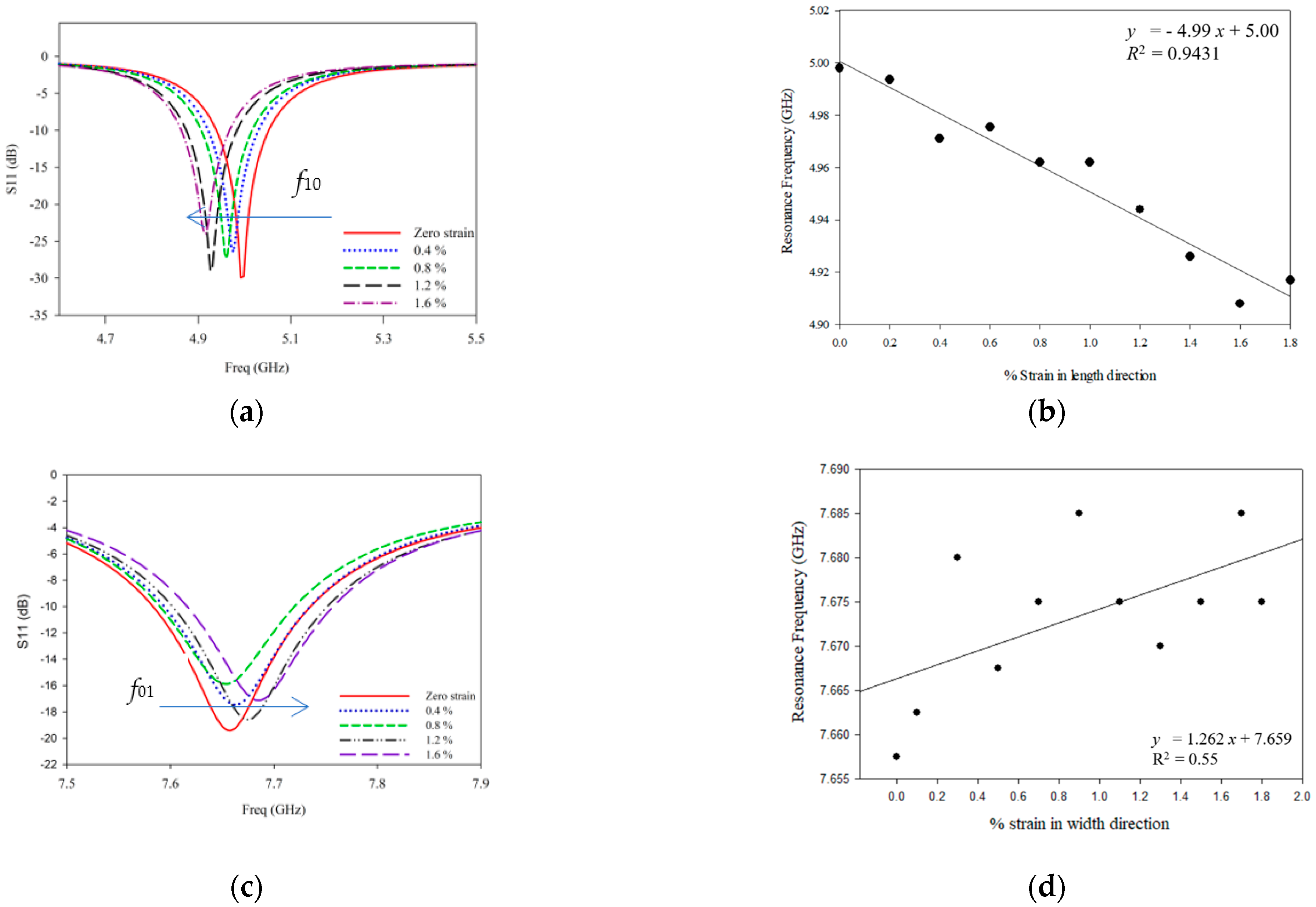
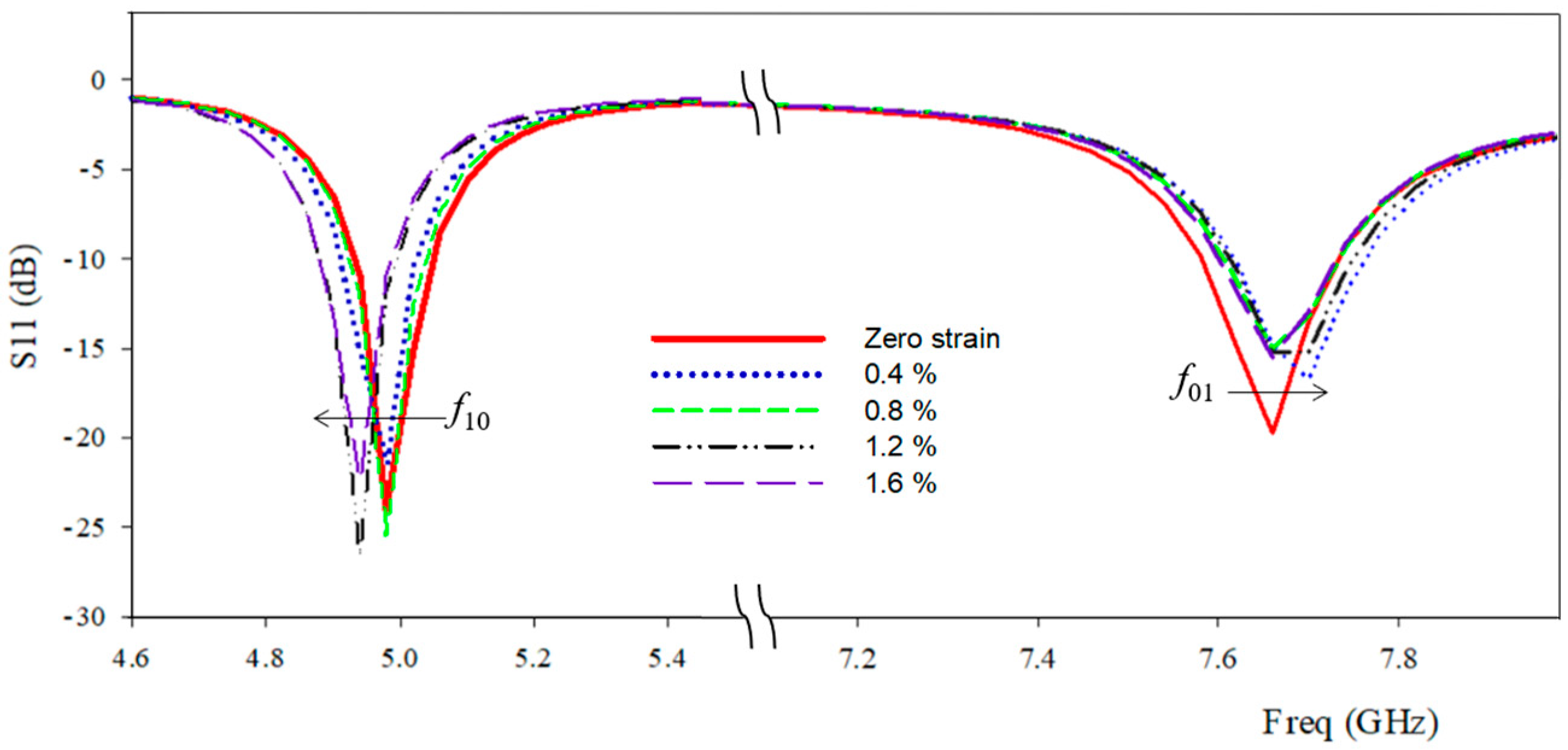
5.1. Strain Sensitivity of Antenna Sensor Subjected to Longitudinal and Transverse Deformations
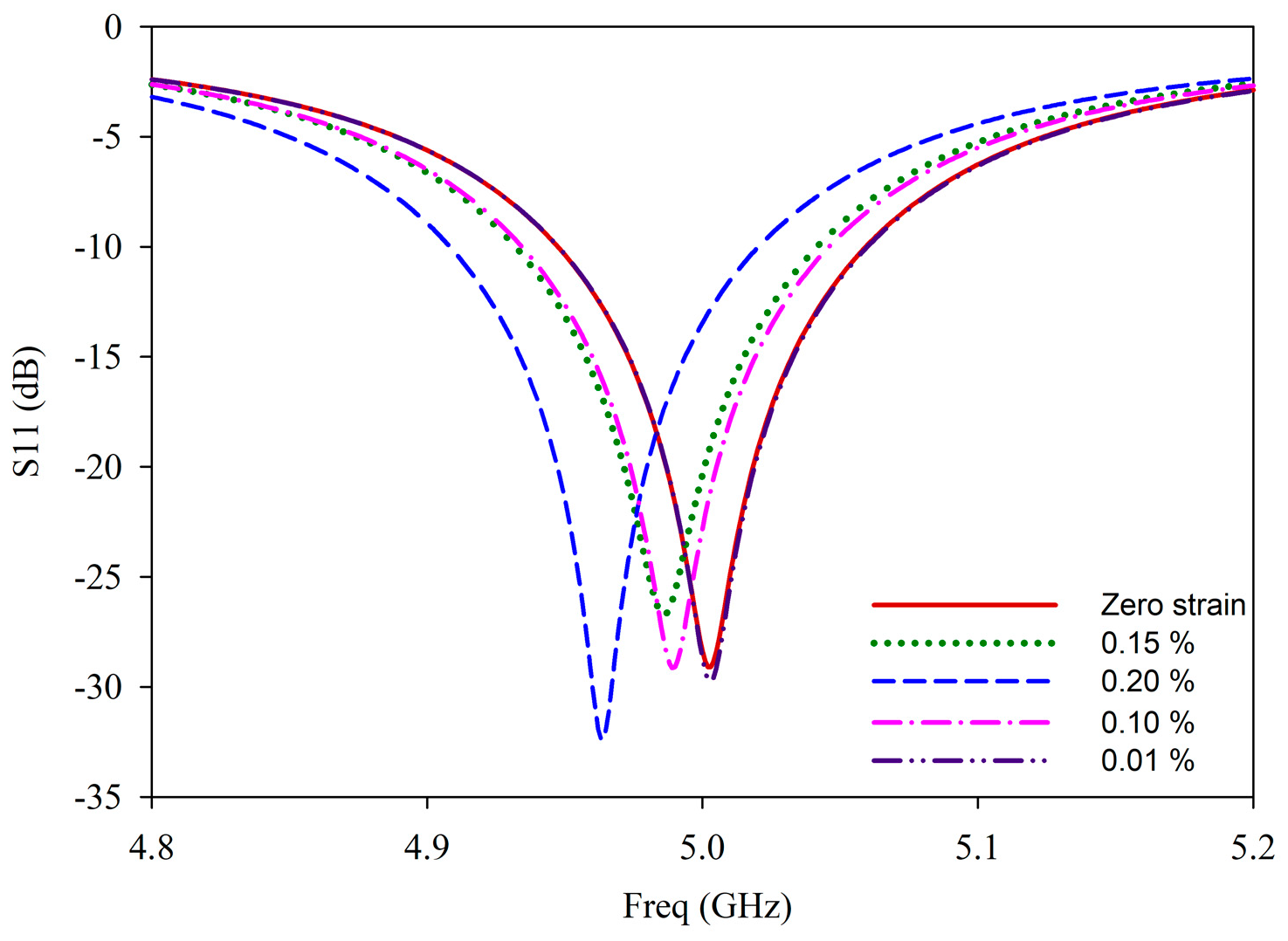
5.2. Sensing Range
5.3. Comparison with the Sensors Available in the Literature
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farrar, C.R.; Worden, K. An Introduction to Structural Health Monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Hashim, K.; Yeboah, D. Recent Advancements in Non-Destructive Testing Techniques for Structural Health Monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Keerthi, M.G.; Shenoy, A.D.; Devanarayanan, B.; Sharath, V.S.; Hariprasad, M.P. Design of Tabletop Automated Plane Polariscope for Digital Photoelastic Measurements; Springer Nature: Heidelberg, Germany, 2022; pp. 675–682. [Google Scholar]
- Bhandari, R. Case study of structural health monitoring in india and its benefits. J. Civ. Eng. Sci. Technol. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Ilyas Rather, A.; Motwani, P.; Laskar, A.; Banerjee, S.; Seng Lok, T.; Lalji Rai, G. Requirements of Indian Guidelines for Structural Health Monitoring. e-J. Nondestruct. Test. 2022, 26541. [Google Scholar]
- Benchirouf, A.; Kanoun, O.; Benchirouf, A.; Zichner, R.; Müller, C.; Kanoun, O. Electromagnetic Simulation of Flexible Strain Sensor Based Microstrip Patch Antenna. Int. J. Microw. Opt. Technol. 2015, 10, 397. [Google Scholar]
- Kumar, P.; Hariprasad, M.P.; Menon, A.; Ramesh, K. Experimental Study of Dry Stone Masonry Walls Using Digital Reflection Photoelasticity. Strain 2020, 56, e12372. [Google Scholar] [CrossRef]
- Harinath Reddy, C.; Mini, K.M.; Radhika, N. Structural Health Monitoring—An Integrated Approach for Vibration Analysis with Wireless Sensors to Steel Structure Using Image Processing; Springer Nature: Heidelberg, Germany, 2019; pp. 1595–1610. [Google Scholar]
- Nisha, M.S.; Venthan, S.M.; Rangasamy, G.; Sam, D.P.; Akilesh, G.; Bhaskar, D.S.; Kumar, N.H. Fabrication and Testing of RGO-PVDF Nano sensing Sheets on Glass Fibre-Reinforced Polymer for Structural Health Monitoring in Aerospace Engineering. Appl. Nanosci. 2023, 13, 5935–5947. [Google Scholar] [CrossRef]
- Chen, H.-P.; Ni, Y.-Q. Introduction to Structural Health Monitoring. In Structural Health Monitoring; Balageas, D., Fritzen, C.-P., Güemes, A., Eds.; ISTE Ltd.: London, UK, 2006; pp. 1–14. [Google Scholar]
- Zhang, B.; Lyu, Y.; Lee, Y. Passive Wireless Strain and Crack Sensing Using a RFID-Based Patch Antenna. J. Phys. Conf. Ser. 2022, 2198, 012018. [Google Scholar] [CrossRef]
- Tchafa, F.M.; Huang, H. Microstrip Patch Antenna for Simultaneous Strain and Temperature Sensing. Smart Mater. Struct. 2018, 27, 065019. [Google Scholar] [CrossRef]
- Tata, U.; Huang, H.; Deb, S.; Wang, J.; Chiao, J.-C. A Patch Antenna-Based Strain Sensor for Structural Health Monitoring. In Proceedings of the SPIE Smart Materials, Nano- and Micro-Smart Systems, Melbourne, Australia, 9–12 December 2008. [Google Scholar]
- Song, G.; Zhang, B.; Lyu, Y.; Wang, X.; Wu, B.; He, C.; Lee, Y.-C. Strain Omnidirectional Detection Based on Circular Patch Antenna. Sens. Actuators A Phys. 2020, 315, 112275. [Google Scholar] [CrossRef]
- Souri, H.; Banerjee, H.; Jusufi, A.; Radacsi, N.; Stokes, A.A.; Park, I.; Sitti, M.; Amjadi, M. Wearable and Stretchable Strain Sensors: Materials, Sensing Mechanisms, and Applications. Adv. Intell. Syst. 2020, 2, 2000039. [Google Scholar] [CrossRef]
- Sanders, J.W.; Yao, J.; Huang, H. Microstrip Patch Antenna Temperature Sensor. IEEE Sens. J. 2015, 15, 5312–5319. [Google Scholar] [CrossRef]
- Tata, U.; Huang, H.; Carter, R.L.; Chiao, J.C. Exploiting a Patch Antenna for Strain Measurements. Meas. Sci. Technol. 2009, 20, 015201. [Google Scholar] [CrossRef]
- Arango Toro, J.; Montes Granada, W.F.; Yepes Zuluaga, S.M. Design and Implementation of a Wearable Patch Antenna That Serves as a Longitudinal Strain Sensor. Text. Res. J. 2021, 91, 2795–2812. [Google Scholar] [CrossRef]
- Gregori, A.; Di Giampaolo, E.; Di Carlofelice, A.; Castoro, C. Presenting a New Wireless Strain Method for Structural Monitoring: Experimental Validation. J. Sens. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Manekiya, M.; Donelli, M.; Kumar, A.; Menon, S.K. A Novel Detection Technique for a Chipless RFID System Using Quantile Regression. Electronics 2018, 7, 409. [Google Scholar] [CrossRef]
- Abdulhussein, A.M.; Khidhir, A.H.; Naser, A.A. 2.4 GHz Microstrip Patch Antenna for S-Band Wireless Communications. J. Phys. Conf. Ser. 2021, 2114, 012029. [Google Scholar] [CrossRef]
- Donelli, M.; Menon, S.; Kumar, A. Compact Antennas for Modern Communication Systems. Int. J. Antennas Propag. 2020, 2020, 1–2. [Google Scholar] [CrossRef]
- Nawaz, H.; Umar Niazi, A. Multi-Port Monostatic Antenna System with Improved Interport Isolation for 2.4GHz Full Duplex MIMO Applications. Electromagnetics 2020, 40, 424–434. [Google Scholar] [CrossRef]
- Wan, C.; Xie, L.; Xu, K.; Xue, S.; Jiang, C.; Wan, G.; Ding, T. Transverse Deformation Effect on Sensitivity of Strain-Sensing Patch Antenna. Int. J. Distrib. Sens. Netw. 2020, 16, 155014772090819. [Google Scholar] [CrossRef]
- Mohammed, A.S.B.; Kamal, S.; Ullah, U.; Mohammed, A.S.; Ahmad, Z.A.; Othman, M.; Hussin, R.; Fariz, M.; Rahman, A. Microstrip Patch Antenna: A Review and the Current State of the Art. J. Adv. Res. Dyn. Control Syst. 2019, 11, 510–524. [Google Scholar]
- Parchin, N.O. Editorial on “Design, Analysis, and Measurement of Antennas”. Appl. Sci. 2023, 13, 10069. [Google Scholar] [CrossRef]
- Ossa-Molina, O.; Duque-Giraldo, J.; Reyes-Vera, E. Strain Sensor Based on Rectangular Microstrip Antenna: Numerical Methodologies and Experimental Validation. IEEE Sens. J. 2021, 21, 22908–22917. [Google Scholar] [CrossRef]
- Herbko, M.; Lopato, P. Microstrip Patch Strain Sensor Miniaturization Using Sierpinski Curve Fractal Geometry. Sensors 2019, 19, 3989. [Google Scholar] [CrossRef] [PubMed]
- Azam, S.A.; Fragoso, A. Experimental and Numerical Simulation Study of the Vibration Properties of Thin Copper Films Bonded to FR4 Composite. Appl. Sci. 2020, 10, 5197. [Google Scholar] [CrossRef]
- Sharma, S.; Tripathi, C.C.; Rishi, R. Impedance Matching Techniques for Microstrip Patch Antenna. Indian J. Sci. Technol. 2017, 10, 1–16. [Google Scholar] [CrossRef]


| Parameters | Description | Dimensions (mm) |
|---|---|---|
| Ls | Substrate length | 60 |
| Ws | Substrate width | 30 |
| h | Substrate thickness | 0.8 |
| Lp | Length of metallic patch | 13.43 |
| Wp | Width of metallic patch | 17.7 |
| Lf | Length of feedline | 13.31 |
| Wf | Width of feedline | 1.52 |
| QL | Length of quarter-wave transformer | 8.43 |
| QW | Width of quarter-wave transformer | 0.34 |
| Dielectric constant | εr | 4.4 |
| Modulus of elasticity (GPa) | E | 20.4 |
| Poisson’s ratio | υ (LW) | 0.12 |
| Length of metallic patch | Lp | 13.43 |
| Loss tangent | tan δ | 0.02 |
| Cross sectional area (mm2) | A (mm2) | 24 |
| Sl No | Ref | Frequency of Operation (GHz) | Structure | Substrate | Type of Loading | Sensitivity | Bidirectional Strain Sensing Capability | Range |
|---|---|---|---|---|---|---|---|---|
| 1 | [17] | 14.9/19.6 | Rectangular patch | Flexible polyimide film (Kapton HN) | Bending | −16.4 kHz/µε | Yes | 0 to 0.5% |
| 2 | [18] | 2.45 | Rectangular | Cotton fabric as a dielectric and conductors made of flexible copper sheets | Tensile | 2.38 MHz/µε | No | - |
| 3 | [24] | 2.45 | Rectangular patch with short circuited vias | RT-5880 | Tensile | −1.730 kHz/µε | Yes (0.640 kHz/µε) | 0 to1.6% |
| 4 | [27] | 2.45 | Rectangular microstrip | FR4 | Tensile | −2.847 kHz/µε | No | 0 to 0.4% |
| 5 | Our work | 5 | Rectangular microstrip | FR4 | Tensile | −4.99 kHz/με | Yes (1.262 kHz/με) | 0.2% to 1.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praveen, A.P.; Babu, J.S.; Menon, S.K.; Hariprasad, M.P. Sensitivity Analysis of an Edge-Fed Microstrip Patch Antenna Strain Sensor to Detect Surface Strains. Eng. Proc. 2025, 93, 8. https://doi.org/10.3390/engproc2025093008
Praveen AP, Babu JS, Menon SK, Hariprasad MP. Sensitivity Analysis of an Edge-Fed Microstrip Patch Antenna Strain Sensor to Detect Surface Strains. Engineering Proceedings. 2025; 93(1):8. https://doi.org/10.3390/engproc2025093008
Chicago/Turabian StylePraveen, A. P., Jeetu S. Babu, Sreedevi K. Menon, and M. P. Hariprasad. 2025. "Sensitivity Analysis of an Edge-Fed Microstrip Patch Antenna Strain Sensor to Detect Surface Strains" Engineering Proceedings 93, no. 1: 8. https://doi.org/10.3390/engproc2025093008
APA StylePraveen, A. P., Babu, J. S., Menon, S. K., & Hariprasad, M. P. (2025). Sensitivity Analysis of an Edge-Fed Microstrip Patch Antenna Strain Sensor to Detect Surface Strains. Engineering Proceedings, 93(1), 8. https://doi.org/10.3390/engproc2025093008







