Wing Design for Class I Mini Unmanned Aerial Vehicles—Special Considerations for Foldable Wing Configuration at Low Reynolds Numbers ^†

Abstract

Foldable wing designs are becoming increasingly popular due to their advantages in the rapid deployment and compact packaging of fixed-wing UAVs, particularly when compared to horizontal take-off and VTOL counterparts. However, selecting an appropriate wing design requires the careful consideration of aerodynamic performance and volume storage constraints. As a result, a trade-off between performance and practicality must be addressed during the conceptual design phase. The primary objective of this study is to identify the optimal wing configuration for a tube-launched foldable wing design. To achieve this, the analysis combine an in-house design tool developed in Excel and XFLR5 v7.01 software.

1. Introduction

Foldable-wing-design UAVs, such as loitering munitions [1], are becoming increasingly popular due to their ease of transportation, compatibility, and minimal operator training required during critical flight phases like take-off. However, specific design considerations must be addressed, particularly regarding the frame’s surfaces, such as the main wing, which must fit within or attach to the fuselage. Additionally, aerodynamic factors like the Reynolds number (below 300,000), which relates to fluid viscosity, play a critical role. In this study, a two-stage analysis is conducted for a given mission profile and selected weight during the conceptual design phase. First, the weight is expressed as a ratio with power (W/P) and surface area (W/S), ensuring that the designed platform meets all performance requirements for key flight attitudes, including stall, cruise, maneuvering, rate of climb, and climb gradient. This stage identifies the acceptable wing area which the designer uses as the basis for the second phase: wing analysis. The airfoil selection stage is streamlined to allow a wide range of Reynolds numbers, enabling the testing of various airfoils using XFLR5 software. The final wing design is selected to meet the desired lift characteristics and achieve an elliptical lift distribution. Lifting-Line Theory (LLT) is applied and compared with LLT and panel methods in XFLR5 for validation. To support rapid and efficient decision-making, the entire design process is automated in Excel using a flow-diagram-like approach inspired by D.P. Raymer [2]. This study represents a key step in the preliminary design of a foldable-wing electric UAV.

2. Concept of Operations—Mission Profile

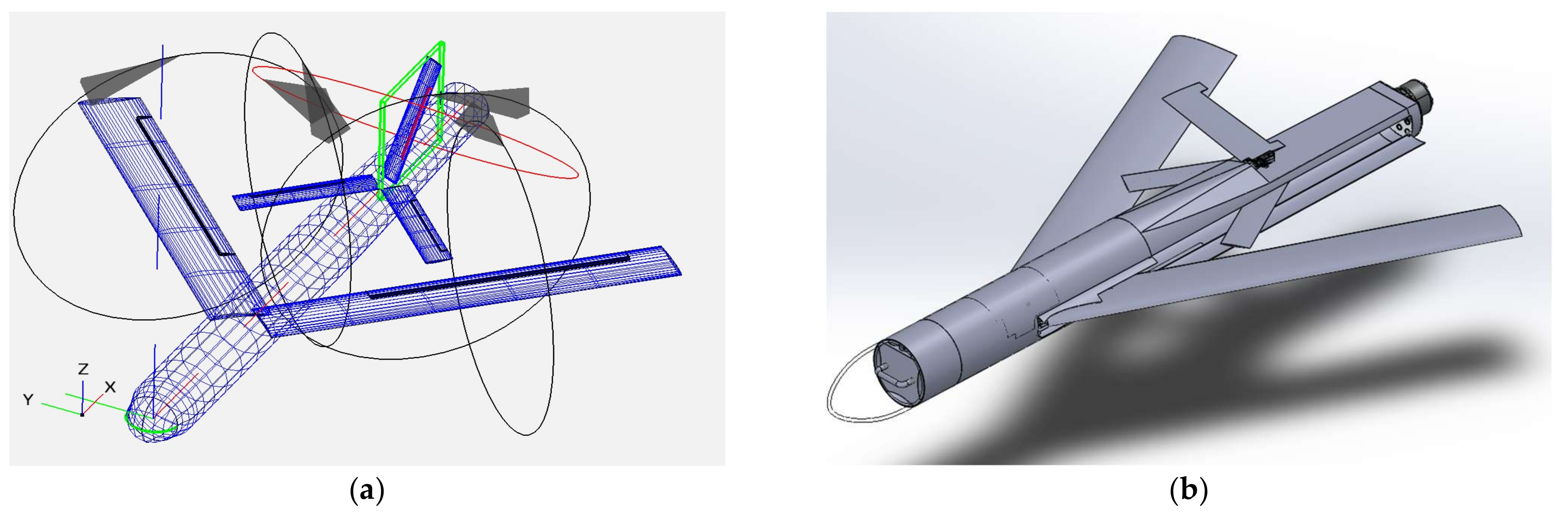
The presented analysis was conducted with the objective of defining the specific requirements for an electric Class I UAV [3] designed for intelligence, reconnaissance, and surveillance (ISR) missions, as depicted in Figure 1. The primary characteristics of the design are flexibility and compatibility, enabling operation by a small team of one or two personnel.

The tube-based design was developed to ensure convenient storage and rapid deployment to the area of interest. A foldable mid-wing configuration, designed to fit inside the fuselage, allows the use of a cylindrical tube barrel. This design choice reduces aerodynamic form drag while maximizing surface area. Additionally, cylindrical barrels are commonly employed in small launchers, particularly in defense applications, offering significant advantages over square cross-section fuselages. These advantages extend to both low and high foldable wing methods, such as those used in the Hero series and Switchblade UAS.

Considering the preceding analysis, the wing design can be distilled into four principal considerations (Figure 2):

• A wing with a tip C_t and root chord C_r lower than the diameter D_f of the fuselage must be used.
• The usage of any form of twist a_t (aerodynamic and geometric) should be reduced. Thus, more space for the vital subsystems will be saved.
• Non-parallel wing folding is applicable for maximum surface area S with different pivot points for each semi-span.
• The total wing semi-span b/2 must be less than 1 m.

The following set of requirements were selected following the methodology that is used at [4], as presented to

Table 1. Weights and lift-to-drag ratio of the proposed high-aspect-ratio UAV.

Symbol	Description	Value
$\mathrm{W}$	MTOM weight (kg)	7.3 (equals ${\mathrm{W}}_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}$)
${\mathrm{W}}_{\mathrm{e}}$ or ${\mathrm{m}}_{\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{t}\mathrm{y}}$	Empty weight (kg)	6.016994205
${\mathrm{W}}_{\mathrm{p}\mathrm{l}}$ or ${\mathrm{m}}_{\mathrm{p}\mathrm{a}\mathrm{y}\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$	Payload weight (kg)	1
${\mathrm{W}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{y}}$ or ${\mathrm{m}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{y}}$	Battery weight (kg)	0.283005795
$\mathrm{L}/{\mathrm{D}}_{\mathrm{M}\mathrm{A}\mathrm{X}}$	Max lift-to-drag ratio	30.17

.

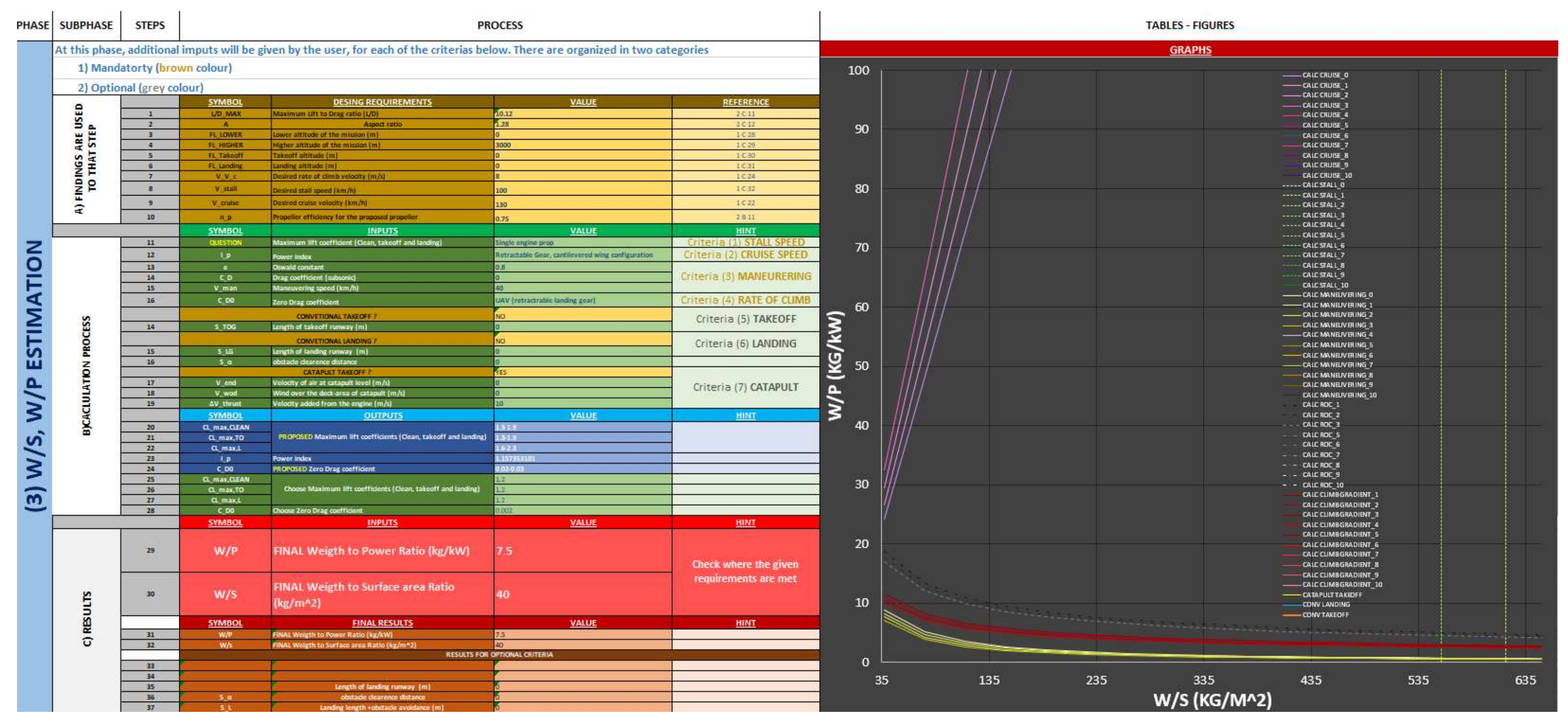
Furthermore, the entire process was developed within an Excel program specifically tailored for electric fixed-wing unmanned aerial systems with propellers. This enables the design team to receive prompt and detailed feedback and, if necessary, revisit and refine the entire design process.

The design program is organized into five distinct categories, separated by a clear upper white line: phase, subphase, step, process, and tables and figures associated with each phase. This structured approach is inspired by project management monitoring methods, such as the Gantt chart. Each logical or numerical value is assigned a unique identifier to ensure clarity and traceability. Phases are numbered from 1 to 1000, subphases are designated with a capital letter (A to Z), and steps are assigned a number between 1 and 1000, each linked to a specific process.

Finally, a color-coding system is implemented to visually distinguish between logical commands, inputs, outputs, and results, as illustrated in Figure 3.

3. W/S vs. W/P Analysis

The weight of the UAV is directly influenced by the surface area and the power required (W/S and W/P matching). The objective is to identify the optimal combination of W/S and W/P by examining five different flight phases: take-off, cruise, and stall speeds; maneuvering; rate of climb; and climb gradient. In [5,6,7], the mathematical proofs of equations are presented and used with a slightly different approach. Moreover, for the purposes of the design, the acceptable load factors adhere to the STANAG airworthiness requirements, as presented in [8], and data for zero drag coefficient are sourced from [9]. Finally, data for international standard conditions (ISA) are used.

The cruise speed criteria are expressed as:

$$(\mathrm{W}/\mathrm{S})/(\mathrm{W}/\mathrm{P})={\mathrm{I}}_{\mathrm{P}}^3\mathsf{\sigma },$$

(1)

where

${\mathrm{I}}_{\mathrm{p}}:$ Index ratio;

$\mathsf{\sigma }$: Ratio between flight leave and sea level.

Similarly, the stall criteria are as follows:

$${\displaystyle \frac{\mathrm{W}}{\mathrm{S}}}={\displaystyle \frac{1}{2}}{\mathsf{\rho }}_{\infty }{\mathrm{V}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{l}}^2{\mathrm{C}}_{{\mathrm{L}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left({\displaystyle \frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^2}}\right),$$

(2)

where

$\mathsf{\rho }:$ Density of air (${\displaystyle \frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^3}}$).

Maneuvering criteria strongly depend on the load factor and subsequently on the adequate thrust-to-weight ratio:

$$\left({\displaystyle \frac{\mathrm{W}}{\mathrm{P}}}\right)={\displaystyle \frac{1}{\frac{\left(\frac{\mathrm{T}}{\mathrm{W}}\right)}{550\times \frac{0.6}{66}}}}0.608277388\mathrm{}({\displaystyle \frac{\mathrm{k}\mathrm{g}}{\mathrm{k}\mathrm{W}}}),\mathrm{}$$

(3)

where

e: Oswald constant.

The rate of climb and climb gradient directly depend on the vertical speed; thus, the zero drag coefficient must be as low as possible:

$$\left({\displaystyle \frac{\mathrm{W}}{\mathrm{P}}}\right)=\mathrm{}{\displaystyle \frac{0.608277388·{\mathrm{n}}_{\mathrm{p}}}{\left(\mathrm{R}\mathrm{C}\mathrm{P}+\frac{\sqrt{\left(\frac{\mathrm{W}}{\mathrm{S}}\right)}}{19·\left((1.345·{\left(\mathrm{A}·\mathrm{e}\right)}^{\frac{3}{4}})/({\mathrm{C}}_{\mathrm{D}\mathrm{o}}^{\frac{1}{4}})\right)·{\mathsf{\sigma }}^{0.5}}\right)}}\left({\displaystyle \frac{\mathrm{k}\mathrm{g}}{\mathrm{k}\mathrm{W}}}\right),$$

(4)

$$\left({\displaystyle \frac{\mathrm{W}}{\mathrm{P}}}\right)0.608277388{\displaystyle \frac{18.97·{\mathrm{n}}_{\mathrm{p}}·{\mathsf{\sigma }}^{0.5}\mathrm{}}{\frac{\left(\mathrm{C}\mathrm{G}\mathrm{R}+{\left(\frac{\mathrm{L}}{\mathrm{D}}\right)}^{-1}\mathrm{}\right)}{{\mathrm{C}}_{\mathrm{L}}^{0.5}}·{\left(\frac{\mathrm{W}}{\mathrm{S}}\right)}^{0.5}}}\left({\displaystyle \frac{\mathrm{k}\mathrm{g}}{\mathrm{k}\mathrm{W}}}\right),$$

(5)

The relevant bibliography defines the optimal area of W/S and W/P as the one that is upright to the diagram. However, to fulfill the special considerations, lower values in the designated area must be used. A high-aspect-ratio design presents a feasible solution. After trial and error, ceilings up to 3000 m with 1000 m pace are examined, and the initial values are $\mathrm{W}/\mathrm{P}\cong 11 \mathrm{k}\mathrm{g}/\mathrm{k}\mathrm{W}$ and $\mathrm{W}/\mathrm{S}\cong 50 \mathrm{k}\mathrm{g}/{\mathrm{m}}^2$ (Figure 4). Thus, this is the design option that will be further examined in the wing design phase. In the next Section, these values are examined in detail.

4. Wing Analysis

Wing selection represents a pivotal and intricate stage of the design process, encompassing a multitude of intricate steps. These can be broadly classified into three principal subphases: airfoil selection, which determines the wing’s aerodynamic characteristics; geometry, which defines the final shape and performance of the wing; and lift distribution analysis, which ensures the structure’s rigidity during flight. Therefore, XFLR5 will be employed to obtain precise results.

4.1. Airfoil Selection

For an efficient wing design, an adequate airfoil both for max and ideal lift coefficient must be selected. For a level cruise flight, these must be

$${\mathrm{C}}_{{\mathrm{L}}_{\mathrm{C}}}={\displaystyle \frac{2\mathrm{W}\mathrm{g}}{\mathsf{\rho }\mathrm{S}{\mathrm{V}}_{\mathrm{c}\mathrm{r}}^2}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{U}\mathrm{A}\mathrm{V};$$

(6)

$${\mathrm{C}}_{{\mathrm{L}}_{{\mathrm{C}}_{\mathrm{W}}}}={\displaystyle \frac{{\mathrm{C}}_{{\mathrm{L}}_{\mathrm{C}}}}{0.95}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g};$$

(7)

$${\mathrm{C}}_{{\mathrm{l}}_{\mathrm{i}}}={\displaystyle \frac{{\mathrm{C}}_{{\mathrm{L}}_{{\mathrm{C}}_{\mathrm{W}}}}}{0.9}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{i}\mathrm{l}.$$

(8)

The maximum lift is achieved near the stall speed. Thus:

$${\mathrm{C}}_{{\mathrm{L}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}={\displaystyle \frac{2\mathrm{W}\mathrm{g}}{\mathsf{\rho }\mathrm{S}{\mathrm{V}}_{\mathrm{c}\mathrm{r}}^2}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{U}\mathrm{A}\mathrm{V},$$

(9)

$${\mathrm{C}}_{{\mathrm{L}}_{{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{w}}}}={\displaystyle \frac{{\mathrm{C}}_{{\mathrm{L}}_{\mathrm{C}}}}{0.95}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g},$$

(10)

$${\mathrm{C}}_{\mathrm{l}\_\max \_\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}}={\displaystyle \frac{{\mathrm{C}}_{{\mathrm{L}}_{{\mathrm{C}}_{\mathrm{W}}}}}{0.9}} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{i}\mathrm{l},$$

(11)

Also, the Reynolds number is given by the following equation:

$$\mathrm{R}\mathrm{e}=\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\rho }{\mathrm{V}}_{\mathrm{c}\mathrm{r}}\overline{\mathrm{C}}}{\mathsf{\mu }}}, \mathrm{a}\mathrm{t} \mathrm{c}\mathrm{r}\mathrm{u}\mathrm{i}\mathrm{s}\mathrm{e} \mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\\ {\displaystyle \frac{\mathsf{\rho }{\mathrm{V}}_{\mathrm{s}}\overline{\mathrm{C}}}{\mathsf{\mu }}}, \mathrm{a}\mathrm{t} \mathrm{s}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{l} \mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\end{array}\right.,$$

(12)

where

$\mathsf{\mu }:$ The dynamic viscosity of the fluid (${\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{s}}}$).

$\mathsf{\sigma }$: The surface area (${\mathrm{m}}^2$).

$\overline{\mathrm{C}}$: The mean aerodynamic chord ($\mathrm{m}$).

Finally, the surface area, wingspan, and mean aerodynamic chord are expressed as follows:

$$\mathrm{S}={\displaystyle \frac{\mathrm{W}}{\frac{\mathrm{W}}{\mathrm{S}}}}\mathrm{}({\mathrm{m}}^2),$$

(13)

$$\mathrm{b}=\sqrt{\mathrm{A}·\mathrm{S}}<1 \mathrm{m},$$

(14)

$$\overline{\mathrm{C}}={\displaystyle \frac{\mathrm{b}}{\mathrm{A}}}<0.1 \mathrm{m},$$

(15)

The precise determination of W/S and W/P will be made in accordance with ${\mathrm{C}}_{{\mathrm{l}}_{\mathrm{i}}}$ and ${\mathrm{C}}_{{\mathrm{l}}_{\mathrm{m}\mathrm{a}\mathrm{x}\_\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}}}$ at the desired cruise altitude, which is 1000 m.

Table 2. Lift coefficients for different power and surface loadings.

$\frac{\mathbf{W}}{\mathbf{P}}\left(\frac{\mathbf{k}\mathbf{g}}{\mathbf{k}\mathbf{W}}\right)$	$\frac{\mathbf{W}}{\mathbf{S}}\left(\frac{\mathbf{k}\mathbf{g}}{{\mathbf{m}}^2}\right)$	$\mathbf{b}\left(\mathbf{m}\right)$	$\overline{\mathbf{C}}\left(\mathbf{m}\right)$	${\mathbf{C}}_{{\mathbf{l}}_{\mathbf{i}}}$ (at 1000 m)	Re (Cruise)	${\mathbf{C}}_{\mathbf{l}\_\mathbf{max} \_\mathbf{g}\mathbf{r}\mathbf{o}\mathbf{s}\mathbf{s}}$ (at 1000 m)	Re (Stall)
13.7	49	1.502	0.099	0.775	226,131.9	1.309	173,947.7
13.5	50	1.487	0.098	0.790	223,847.8	1.336	172,190.6
13.4	51	1.473	0.097	0.806	221,563.6	1.363	170,433.6
13.3	52	1.458	0.096	0.822	219,279.5	1.389	168,676.5
13.2	53	1.445	0.095	0.838	216,995.3	1.417	166,919.5
13	54	1.431	0.094	0.854	214,711.2	1.443	165,162.4

presents a more comprehensive analysis of the selected values from Figure 2. A series of trials was conducted with a variety of NACA, GOE, ELLPER and FX series airfoils, utilizing XFLR5 software, with the objective of identifying the optimal option for an Re range of 215,000 to 226,000. Of the two candidates, NACA 5508 and GOE 173, the latter presents superior characteristics, offering enhanced longitudinal control and endurance due to its high moment coefficient and lift-to-drag ratio. Based on these considerations, the latter option will be selected (Figure 5). Moreover, GOE 173 is a thin, highly cambered airfoil that can be folded into the fuselage, and it is also ideal for use in lightweight construction. The resulting unmanned aircraft will be more controllable and agile, allowing the operator to efficiently recon the desired area.

4.2. Wing Configuration Selection

For the purpose of the analysis, six different wing geometry configurations are examined, two untapered, two tapered with no sweep in the middle of the chord (symmetrically tapered), and two tapered with sweep in the middle of the chord (swept tapered wing). The characteristics of each wing option are given by the following set of equations:

$$\lambda =\left\{\begin{array}{l}\mathsf{\lambda }=1, \mathrm{u}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\\ \mathsf{\lambda }<1, \mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\end{array}\right.$$

(16)

$$\mathsf{\Lambda }=\left\{\begin{array}{c}{\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}={\mathsf{\Lambda }}_{\mathrm{C}/4 }={\mathsf{\Lambda }}_{\mathrm{C}/2 }=0 \left(\mathrm{d}\mathrm{e}\mathrm{g}\right), \mathrm{u}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\\ {\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}<0,{\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}>0, {\mathsf{\Lambda }}_{\mathrm{C}/4 }<>0 \mathrm{and} {\mathsf{\Lambda }}_{\mathrm{C}/2 }=0, \mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y} \mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\hspace{1em}\\ {\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}<0,{\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}>0, {\mathsf{\Lambda }}_{\mathrm{C}/4 }<>0 \mathrm{and} {\mathsf{\Lambda }}_{\mathrm{C}/2 }<>0 \mathrm{s}\mathrm{w}\mathrm{e}\mathrm{p}\mathrm{t} \mathrm{t}\mathrm{a}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\end{array}\right.$$

(17)

$${\mathrm{C}}_{\mathrm{r}}=\left\{\begin{array}{c}{\mathrm{C}}_{\mathrm{r}}=\overline{\mathrm{C}}={\displaystyle \frac{\mathrm{b}}{\mathrm{A}}}, \mathrm{u}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\\ {\mathrm{C}}_{\mathrm{r}}={\displaystyle \frac{3}{2}}\left({\displaystyle \frac{\overline{\mathrm{C}}\left(1+\mathsf{\lambda }\right)}{1+\mathsf{\lambda }+{\mathsf{\lambda }}^2}}\right),\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{s}\mathrm{w}\mathrm{e}\mathrm{p}\mathrm{t} \mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\end{array}\right.$$

(18)

$${\mathrm{C}}_{\mathrm{t}}=\left\{\begin{array}{c}{\mathrm{C}}_{\mathrm{t}}=\overline{\mathrm{C}}={\displaystyle \frac{\mathrm{b}}{\mathrm{A}}}, \mathrm{u}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\\ {\mathrm{C}}_{\mathsf{\tau }}=\mathsf{\lambda }·{\mathrm{C}}_{\mathrm{r}},\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{y} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{s}\mathrm{w}\mathrm{e}\mathrm{p}\mathrm{t} \mathrm{t}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{g}\end{array}\right.$$

(19)

where

$\mathsf{\lambda }:$ Taper ratio;

${\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}$: Sweep of the wing at the leading edge (deg);

${\mathsf{\Lambda }}_{\mathrm{c}/4}$: Sweep of the wing at the quarter chord (deg);

${\mathsf{\Lambda }}_{\mathrm{c}/2}$: Sweep of the wing at the half chord (deg);

${\mathrm{C}}_{\mathrm{r}}$: Root chord (deg);

${\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}$: Sweep of the wing at the leading edge (deg);

${\mathsf{\Lambda }}_{\mathrm{L}\mathrm{E}}$: Sweep of the wing at the leading edge (deg).

4.3. Lift Distribution Analysis

In addition to geometric characteristics, the distribution of lift is the primary criterion for wing selection. Lifting-Line Theory, as presented in [8] (pp. 242–246), is employed to evaluate and compare the six selected wing designs.

Table 3. Wing options for the UAV.

Option	$\mathit{\Gamma }$	${\mathit{i}}_{\mathit{w}}$ (Deg)	${\mathit{\alpha }}_{\mathit{t}}$ (Deg)	$\mathsf{\lambda }$	${\mathsf{\Lambda }}_{\mathit{c}/2}$ (Deg)	${\mathit{C}}_{\mathit{l}}$ (Calculated)	${\mathit{C}}_{\mathit{L}}$ (Calculated)
1	0	4.45	0	1	0	0.834776	83.36302
2	0	4.8	−0.4	1	0	0.834728	83.35823
3	0	4.66	0	0.91	0	0.837885	83.67355
4	0	5.02	−1	0.91	0	0.837725	83.65752
5	0	4.66	0	0.91	5	0.837533	83.63839
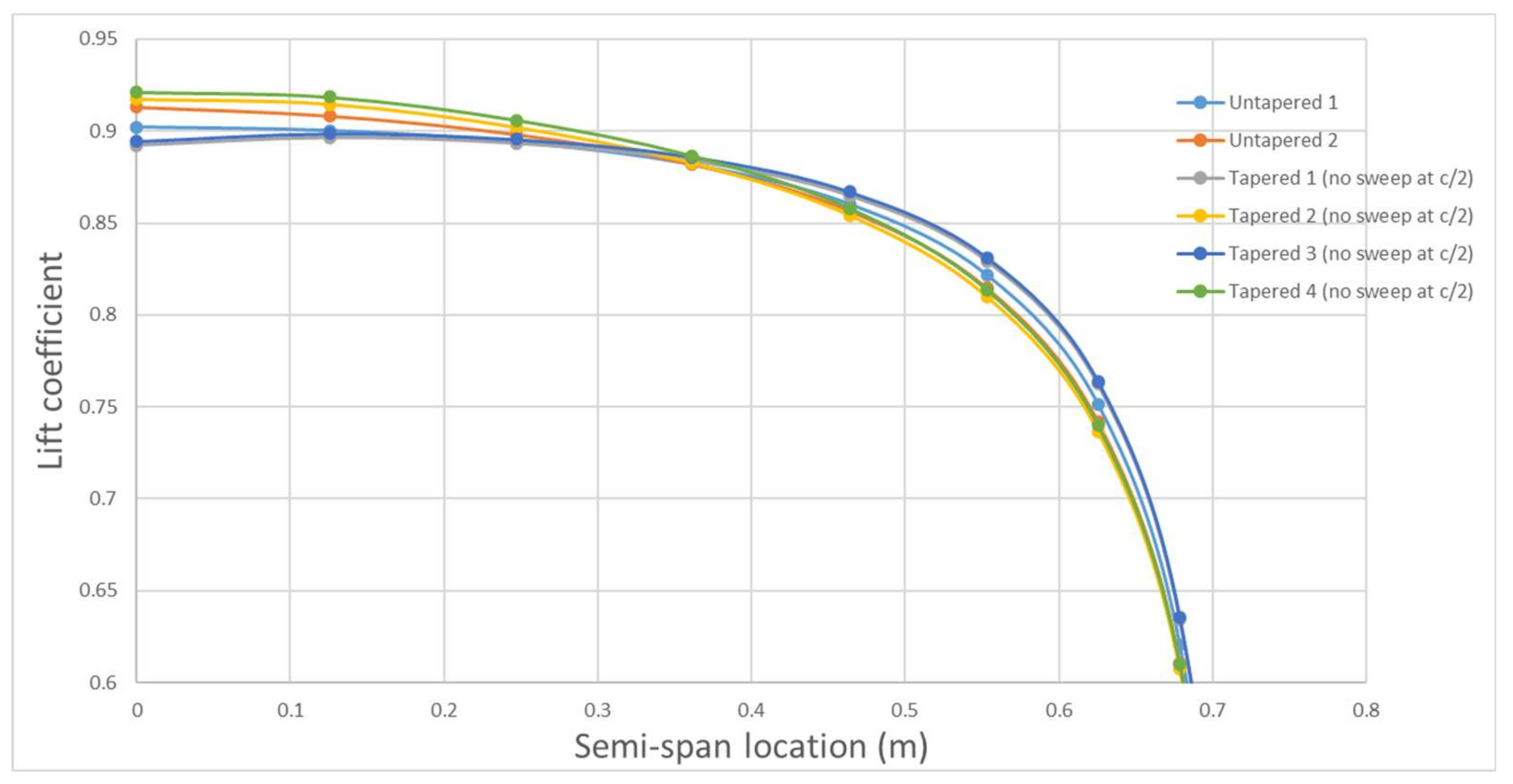
6	0	4.9	−1	0.91	5	0.838209	83.70591

provides the total calculated lift for each wing, while Figure 4 illustrates the lift distribution along the semi-span.

The maximum feasible taper ratio for the design is determined to be λ = 0.91, based on the design requirements and the maximum acceptable chord root value (${\mathrm{C}}_{\mathrm{r}}$ = 0.0998). The incidence angle has a dynamic relationship with the twist angle (α_t). Incorporating twist improves stall characteristics and results in a more elliptical lift distribution; however, it directly increases the incidence angle, particularly in tapered wing designs. As a result, a trade-off must be made, and an inevitable increase in the incidence angle is selected, which also minimizes the volume occupied within the fuselage.

Furthermore, incorporating sweep without applying a twist angle negatively impacts the lift distribution. Based on these findings, Option 2 appears to be the most suitable for the design requirements, offering an optimal balance between minimal twist usage and superior lift distribution compared to the other options (Figure 6).

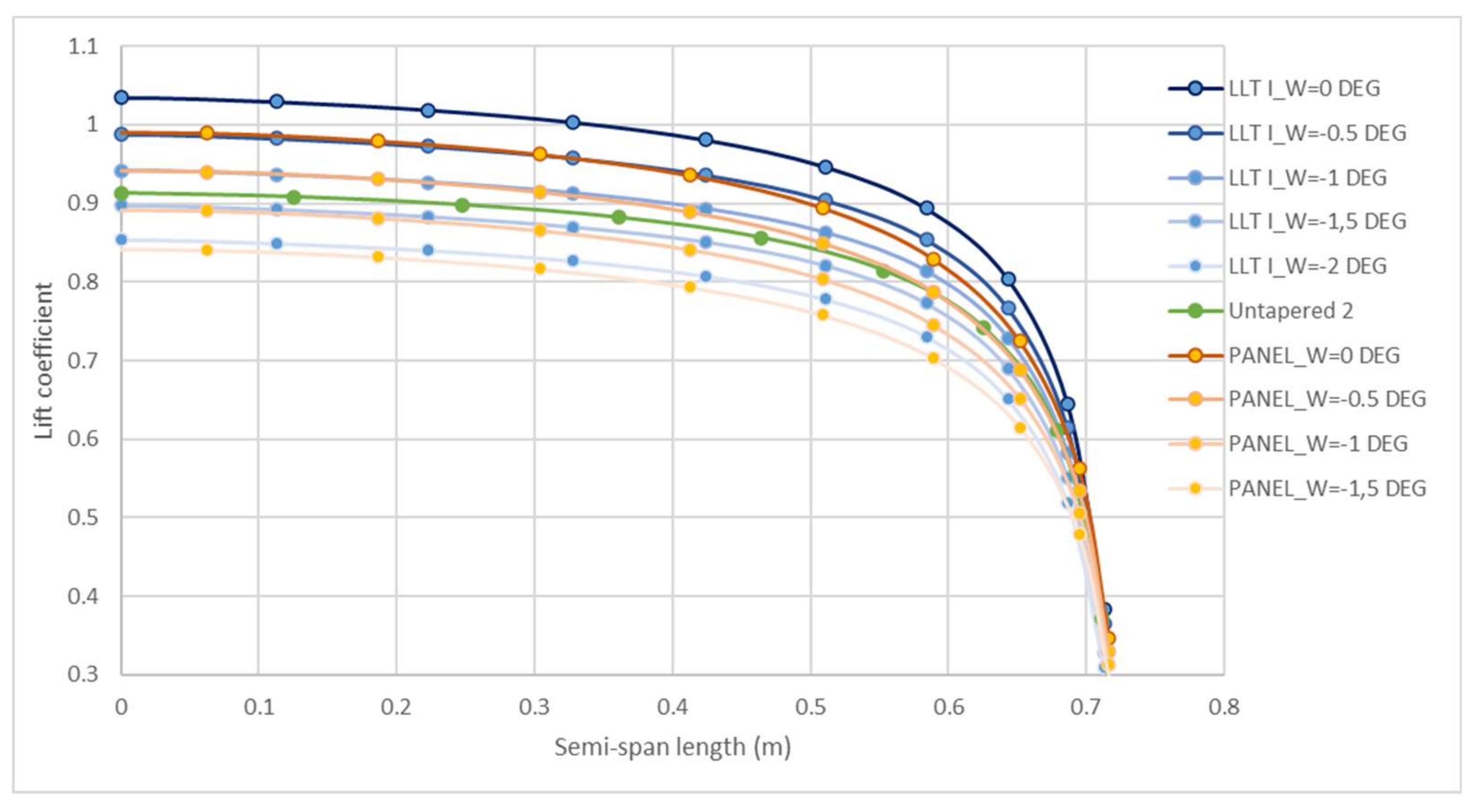
5. Comparison of Different Lifting Distribution Calculus

The chosen method for calculating wing design provides designers with an initial estimate of the desired design. While the values may be overestimated, they still offer a preliminary approximation of the real values. XFLR5 can be used to gain insight into these differences. When running an analysis in this program for the same selected wing (Option 2), using Lifting Line-Theory (LLT) and Panel, and comparing the results with the presented method, it is evident that smaller incidence angles are required to achieve the ideal lift coefficient. As shown in the lift distribution plot in Figure 7, the first method indicates an angle of attack ranging from −2 to −1.5 degrees (approximately 2.8 to 3.3 degrees of incidence), while the latter indicates an angle of −1.5 to −1 degrees (approximately 3.3 to 3.8 degrees of incidence). The accuracy of our calculation is confirmed by the elliptical form in all theories.

6. Conclusions

The trade-off between optimal performance and functionality in folding wing design is challenging. However, the presented method can be used as a first step in this direction. In addition, the Excel program provides a quick decision-making platform for designers. A way forward is to analyze more airfoils, such as [10], and different fuselage cross-sections (i.e., square) to compare results with real flight tests.