Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance †
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Methodology
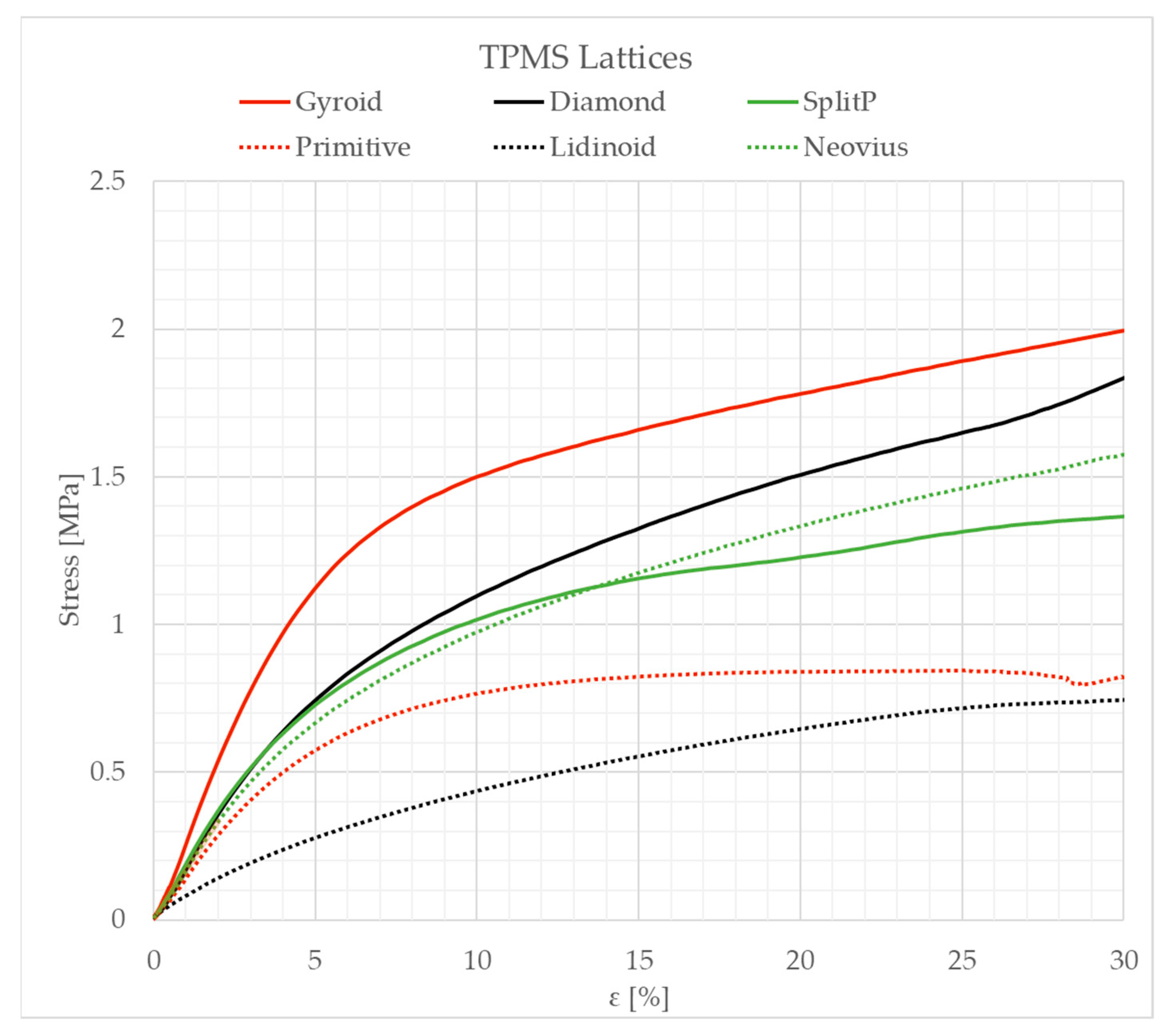
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fisher, J.W.; Miller, S.W.; Bartolai, J.; Simpson, T.W.; Yukish, M.A. Catalog of triply periodic minimal surfaces, equation-based lattice structures, and their homogenized property data. Data Brief 2023, 49, 109311. [Google Scholar] [CrossRef] [PubMed]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, X.; Yang, Y.; Yang, X.; Yi, Y. Mechanical behavior of TPMS-based scaffolds: A comparison between minimal surfaces and their lattice structures. SN Appl. Sci. 2019, 1, 1145. [Google Scholar] [CrossRef]
- Benedetti, M.; Plessis, A.D.; Ritchie, R.O.; Dallago, M.; Razavi, S.M.J.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Gado, M.G.; Al-Ketan, O.; Aziz, M.; Al-Rub, R.A.; Ookawara, S. Triply Periodic Minimal Surface Structures: Design, Fabrication, 3D Printing Techniques, State-of-the-Art Studies, and Prospective Thermal Applications for Efficient Energy Utilization. Energy Technol. 2024, 12, 2301287. [Google Scholar] [CrossRef]
- Pugliese, R.; Graziosi, S. Biomimetic scaffolds using triply periodic minimal surface-based porous structures for biomedical applications. SLAS Technol. 2023, 28, 165–182. [Google Scholar] [CrossRef]
- Hyde, S.; Blum, Z.; Landh, T.; Lidin, S.; Ninham, B.W.; Andersson, S.; Larsson, K. The Language of Shape: The Role of Curvature in Condensed Matter: Physics, Chemistry and Biology; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Lodhi, S.K.; Gill, A.Y.; Hussain, I. 3D Printing Techniques: Transforming Manufacturing with Precision and Sustainability. Int. J. Multidiscip. Sci. Arts 2024, 3, 129–138. [Google Scholar] [CrossRef]
- Jin, M.; Feng, Q.; Fan, X.; Luo, Z.; Tang, Q.; Song, J.; Ma, S.; Nie, Y.; Jin, P.; Zhao, M. Investigation on the mechanical properties of TPMS porous structures fabricated by laser powder bed fusion. J. Manuf. Process 2022, 76, 559–574. [Google Scholar] [CrossRef]
- Miralbes, R.; Ranz, D.; Pascual, F.; Zouzias, D.; Maza, M. Characterization of additively manufactured triply periodic minimal surface structures under compressive loading. Mech. Adv. Mater. Struct. 2020, 29, 1841–1855. [Google Scholar] [CrossRef]
- Karimipour-Fard, P.; Behravesh, A.H.; Jones-Taggart, H.; Pop-Iliev, R.; Rizvi, G. Effects of design, porosity and biodegradation on mechanical and morphological properties of additive-manufactured triply periodic minimal surface scaffolds. J. Mech. Behav. Biomed. Mater. 2020, 112, 104064. [Google Scholar] [CrossRef]
- Sauermoser-Yri, M.; Veldurthi, N.; Wölfle, C.H.; Svartvatn, P.J.; Hoem, S.O.F.; Lid, M.J.; Bock, R.; Palko, J.W.; Torgersen, J. On the porosity-dependent permeability and conductivity of triply periodic minimal surface based porous media. J. Mater. Res. Technol. 2023, 27, 585–599. [Google Scholar] [CrossRef]
- Song, K.; Wang, Z.; Lan, J.; Ma, S. Porous structure design and mechanical behavior analysis based on TPMS for customized root analogue implant. J. Mech. Behav. Biomed. Mater. 2021, 115, 104222. [Google Scholar] [CrossRef] [PubMed]
- Qiu, N.; Wan, Y.; Shen, Y.; Fang, J. Experimental and numerical studies on mechanical properties of TPMS structures. Int. J. Mech. Sci. 2024, 261, 108657. [Google Scholar] [CrossRef]
- Khanna, P.; Sood, S.; Mishra, P.; Bharadwaj, V.; Aggarwal, A.; Singh, S.J. Analysis of compression and energy absorption behaviour of SLM printed AlSi10Mg triply periodic minimal surface lattice structures. Structures 2024, 64, 106580. [Google Scholar] [CrossRef]
- Sun, Q.; Sun, J.; Guo, K.; Wang, L. Compressive mechanical properties and energy absorption characteristics of SLM fabricated Ti6Al4V triply periodic minimal surface cellular structures. Mech. Mater. 2022, 166, 104241. [Google Scholar] [CrossRef]
- Daynes, S. Isotropic cellular structure design strategies based on triply periodic minimal surfaces. Addit. Manuf. 2024, 81, 104010. [Google Scholar] [CrossRef]
- Mishra, A.K.; Chavan, H.; Kumar, A. Effect of material variation on the uniaxial compression behavior of FDM manufactured polymeric TPMS lattice materials. Mater. Today Proc. 2021, 46, 7752–7759. [Google Scholar] [CrossRef]
- Saleh, M.; Anwar, S.; Al-Ahmari, A.M.; Alfaify, A. Compression Performance and Failure Analysis of 3D-Printed Carbon Fiber/PLA Composite TPMS Lattice Structures. Polymers 2022, 14, 4595. [Google Scholar] [CrossRef]
- Mishra, A.K.; Kumar, A. Compression Behavior of Triply Periodic Minimal Surface Polymer Lattice Structures. Exp. Mech. 2023, 63, 609–620. [Google Scholar] [CrossRef]
- Cao, Y.; Lai, S.; Wu, W.; Sang, L.; Lin, Y.; Liu, T.; Liang, C.; Liu, W.; Zhao, Y. Design and mechanical evaluation of additively-manufactured graded TPMS lattices with biodegradable polymer composites. J. Mater. Res. Technol. 2023, 23, 2868–2880. [Google Scholar] [CrossRef]
- Guttridge, C.; Shannon, A.; O’Sullivan, A.; O’Sullivan, K.J.; O’Sullivan, L.W. Effects of post-curing duration on the mechanical properties of complex 3D printed geometrical parts. J. Mech. Behav. Biomed. Mater. 2024, 156, 106585. [Google Scholar] [CrossRef] [PubMed]
- ASTM D695; Standard Test Method for Compressive Properties of Rigid Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2023.


| TPMS Geometry | Wall Thickness (mm) |
|---|---|
| Neovius | 0.31 |
| Lidinoid | 1.17 |
| Primitive | 1.31 |
| SplitP | 1.33 |
| Diamond | 1.94 |
| Gyroid | 2.32 |
| Pattern Name | Pattern | |
|---|---|---|
| Gyroid |  | |
| Primitive |  | |
| Diamond |  | |
| Lidinoid |  | |
| SplitP |  | |
| Neovius’ surface |  | 3 |
| Structure | Wall Thickness [mm] | Young’s Modulus [MPa] | Standard Deviation [MPa] | Energy Absorption at 30% Strain [MPa] |
|---|---|---|---|---|
| Gyroid | 2.32 | 25.44 | 0.049 | 0.453 |
| Diamond | 1.94 | 17.61 | 0.041 | 0.365 |
| SplitP | 1.33 | 18.78 | 0.022 | 0.310 |
| Primitive | 1.31 | 14.35 | 0.041 | 0.216 |
| Lidinoid | 1.17 | 7.65 | 0.039 | 0.152 |
| Neovius | 0.31 | 16.70 | 0.037 | 0.323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavafaki, S.; Maliaris, G. Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance. Eng. Proc. 2025, 87, 46. https://doi.org/10.3390/engproc2025087046
Kavafaki S, Maliaris G. Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance. Engineering Proceedings. 2025; 87(1):46. https://doi.org/10.3390/engproc2025087046
Chicago/Turabian StyleKavafaki, Sofia, and Georgios Maliaris. 2025. "Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance" Engineering Proceedings 87, no. 1: 46. https://doi.org/10.3390/engproc2025087046
APA StyleKavafaki, S., & Maliaris, G. (2025). Mechanical Characterization of Triply Periodic Minimal Surface Structures Fabricated via SLA 3D Printing Using Tough Resin: Influence of Geometry on Performance. Engineering Proceedings, 87(1), 46. https://doi.org/10.3390/engproc2025087046







