Psychophysiological Analysis of Correction Calculation for as Turbine Engine Gas Turbine Engine Noise Tonality ^†

Abstract

In this paper, we duct a psychophysiological and methodological analysis of the calculation of tonality correction during bench tests of aircraft gas turbine engines for compliance with environmental noise requirements. It is proven that the noise characteristics of a signal are influenced by the modulation law of its tonal components. It is shown that the application of the spectral analysis method for gas turbine engine acoustic signals, for which the stationarity parameters are not determined, leads to an uncertain systematic error. The calculation of the tonality parameter value, which determines the correction of deterioration of the environmental impact assessment of the engine, is not substantiated and has a random character. This paper presents a methodology for the psychophysiological ranking of gas turbine engine noise signals, which offers an intelligent algorithm for signal processing that corresponds with that corresponds with the speech zones of the human central nervous system.

1. Problem Statement

When developing and modifying aircraft gas turbine engines (GTEs), importance is increasingly attached to the task of meeting the requirements of ICAO, an international organization, and ACARE, the Advisory Council for Aeronautical Research in Europe, aimed at reducing harmful emissions into the environment, including noise [1,2]. The requirement of limiting engine noise affects both the overall design of the engine’s own systems and their interaction with aircraft systems.

The purpose of this paper is to give an objective account of GTE noise levels at the stage of bench tests, which will allow us to assess the expected noise level as part of the aircraft building process.

The work is performed to evaluate the results of research in the field of reducing aircraft noise in accordance with Task No. 3 SRIA ACARE [2,3] on environmental protection and energy supply, as well as to achieve the ACARE Flightpath 2050 goal [4]—to reduce aircraft noise by 65% (−52EPNdB) by 2050 by 2050 compared to 2000.

In applicable standard methodological documents [1], there is a classification of noise according to time and frequency characteristics. The classification is based on a set of noise signal parameters and ranks noise according its level of negative effects on human’s physiological state. At the same time, the frequency components of GTE noise in the normalized frequency range are divided into deterministic and pseudorandom ones, which are classified as tonal components. The variability value of tonality amplitude determines the correction of deterioration of environmental impact assessments of GTEs, whose values range 3 to 7 dB, which, in most cases, is sufficient to essentially change the result of noise examination or state the inefficiency of the implemented modifications of the engine.

The noise signal parameters that determine the tonality effect are determined in one-third octave spectral bands and assume a difference in adjacent bands from 3 dB to 10 dB, depending on the methodology of the standard used. Unfortunately, the currently used definitions and criteria for the technical noise of tonal components do not always correlate with each other, which results in results in incomplete determination of the processes of the impact of the tonal components of noise on its environmental assessment.

Therefore, the rationale for applying tonality correction deserves careful consideration from the perspectives of both psychophysiological assessment of impact of noise signal parameters and the methods for its processing.

2. Response of Auditory System to Acoustic Signals

Acoustic signals perceived by a human can be divided into three groups according to their effect on the body’s state: neutral signals—have no effect; favorable signals—improve the state and unfavorable signals—aggravate the state. The first group is not included in the scope of the analysis in this work. The second group includes the sounds of speech, nature and musical signals; the third group is represented by all signals defined as the noise of vehicles and machinery in standard documents [1] for noise examination.

It is proven that industrial noise, characterized by a sound pressure of 70 dB, causes disorders of the endocrine and nervous systems. However, the pressure of symphonic orchestra acoustic signals is estimated to be 75–80 dB, and its sound is classified as having a favorable effect. In order to explain this contradiction, we will conduct a brief analysis of the function of the human auditory system when receiving favorable acoustic signals, namely speech or musical signals.

Studies of the human auditory system are based on the spectral model of speech signals in a tonal frequency band (150–7100 Hz), which covers the frequencies of the first three formants and antiformants. The model is adequate for investigating natural processes as a first approximation, in which the volumetric acoustic parameters of speech signals are analyzed, in particular, the pressure and material density of the communication acoustic channel. The variation in the acoustic pressure energy ${\mathrm{E}}_{\mathrm{s}}(\mathrm{t})$ in the communication channel material over time defines the information $\mathrm{I}(\mathrm{t})=\mathrm{f}\left[{\mathrm{E}}_{\mathrm{s}}(\mathrm{t})\right]$ of the speech or musical signal $\mathrm{s}(\mathrm{t})$. The speech process [5] can be presented as a mathematical model of carrier signal ${\mathrm{s}}_{\mathrm{g}}(\mathrm{t})$ modulation by modulating function $\mathrm{I}(\mathrm{t})$:

$$\begin{array}{l}\mathrm{s}(\mathrm{t})=\mathrm{M}\mathrm{d}\left[\mathrm{I}(\mathrm{t}),{\mathrm{s}}_{\mathrm{g}}(\mathrm{t})\right],\\ {\mathrm{s}}_{\mathrm{g}}(\mathrm{t})=\mathrm{f}(\mathrm{t},{\mathrm{a}}_{\mathrm{i}}),\mathrm{i}\in 1\dots \mathrm{n},\end{array}$$

(1)

where $\mathrm{M}\mathrm{d}[\dots ]$ is the modulation operator, and ${\mathrm{a}}_{\mathrm{i}}$ is the parameter determining the carrier signal shape.

Models of the auditory system [6] consider the process of receiving acoustic signals based on the concepts of classical aerodynamics, i.e., they analyze the average of a certain volume $\mathrm{V}$ of the communication channel material parameters of velocity $\overrightarrow{\mathrm{v}}(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{t})$, pressure $\overrightarrow{\mathrm{p}}(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{t})$ and density $\overrightarrow{\mathsf{\rho }}(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{t})$ gradients. Considering that these parameters are related to each other through the Laplace formula for sound velocity, and acoustic–electrical amplifiers are sensitive to pressure gradient variation, expression (1) can be presented as $\mathrm{s}(\mathrm{t})=\mathrm{M}\mathrm{d}\left[\mathrm{I}(\mathrm{t}),\overrightarrow{\mathrm{p}}(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{t})\right]$. Thus, a continuous model (2) of acoustically favorable sound ${\mathrm{s}}_{\mathrm{m}}(\mathrm{t})$ can be presented as the following expression [5]:

$$\begin{array}{l}\mathrm{k}(\mathrm{t})={\displaystyle \sum _{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}(\mathrm{t})\cos [{\mathsf{\omega }}_{\mathrm{ki}}\mathrm{t}+{\mathsf{\Psi }}_{\mathrm{i}}(\mathrm{t})}]=\mathrm{f}[\mathrm{I}(\mathrm{t})],\\ {\mathrm{s}}_{\mathrm{m}}(\mathrm{t})=\mathrm{M}{\mathrm{d}}_{\mathsf{\Psi }}\left[\mathrm{k}(\mathrm{t}),{\displaystyle \sum _{\mathrm{j}}{\mathrm{s}}_{\mathrm{f}\mathrm{o}{\mathrm{r}}_{\mathrm{j}}}({\mathsf{\omega }}_{\mathrm{f}\mathrm{o}{\mathrm{r}}_{\mathrm{j}}},\mathrm{t})}\right],\\ \mathrm{t}\in (\mathrm{T}\mathrm{p}],\end{array}$$

(2)

where ${\mathsf{\Psi }}_{\mathrm{i}}(\mathrm{t})$ and ${\mathsf{\omega }}_{{\mathrm{k}}_{\mathrm{i}}}$ represent the phase angle and angular frequency of $\mathrm{i}$—the kineme; $\mathrm{g}({\mathsf{\omega }}_{\mathrm{f}\mathrm{o}{\mathrm{r}}_{\mathrm{i}}},\mathrm{t})$ is the carrier signal of $\mathrm{j}$—the formant; and $\mathrm{T}\mathrm{p}$ is the stationarity interval. Signal ${\mathrm{s}}_{\mathrm{m}}(\mathrm{t})$ belongs to the Hilbert space with finite power ${\mathrm{N}}_{\mathrm{m}}({\mathsf{\omega }}_{\mathrm{g}},\mathrm{t}),\mathrm{t}\in (\mathrm{T}\mathrm{p}]$ within the time interval $\mathrm{T}\mathrm{p}$. Its spectral function in the frequency band does not contain delta functions or discontinuities.

An example of an information-modulated signal is shown in Figure 1 as a time function of acoustic pressure when pronouncing the word “akula” (shark, ukr.) in Ukrainian.

The auditory system is a receiver of information, i.e., the form and information content of acoustic signals. The most accessible and best studied [7] aspects are the physiological organs and signal processing processes in the peripheral part of the auditory system, which, according to modern theories, performs the function of an amplitude-adaptive acoustic–mechanical amplifier (middle ear). This amplifier, under the control of the central nervous system (CNS), non-linearly changes the complex transmission coefficient of the psychophysiological analyzer of signal parameters and the mechanical–electrical converter (inner ear receptor—labyrinth). The labyrinth, in turn, identifies the informational signs of the signal and transforms them into discrete binary electrical impulses that arrive via nerve fibers in the Wernicke area of the CNS.

In the Wernicke area, the received signal is compared with previously accumulated information signals. If the received signal coincides with the one from the accumulated database, an otoacoustic emission signal [8] is generated, which arrives at the inner ear receptor. It controls the outer hair cells of the main membrane of the inner ear and is an internal image (for the receptor—CNS) of the identified signal. This process can be represented as the optimal (correlation) reception of the time function of the acoustic signal. Particular attention should be paid to semicircular canals, which are sensors of balance and the body’s position in space. The canals are hydraulically connected to the cavity of the inner ear by the perilymph substance. This connection explains the loss of balance and orientation of a human in space when exposed to high-level pulsed sounds. It is important to point out that the otoacoustic emission signal compensates for oscillations of the main membrane of the cochlea such that there is no movement of the tympanic membrane and perilymph circulation in the area of semicircular canals.

Musical acoustic signals, like speech ones, can be described by model (2). They consist of a finite number of note signals with different carrier frequencies, whose amplitude does not change, or changes slightly in accordance with the attenuation decrement of musical instruments.

For the case of an aircraft being in the phase of takeoff or landing, it is also necessary to take into account the Doppler effect both for the aircraft speed and the wind speed. The wind speed component is random and summed vectorially with the aircraft speed. The model of this signal describes a process with random parameters, so model (2) can be represented by the following Formula (3):

$$\begin{array}{l}\mathrm{s}(\mathrm{t})=\mathrm{M}{\mathrm{d}}_{\mathsf{\Psi }}\left[{\mathrm{k}}_{\mathrm{n}}(\mathrm{t}),{\displaystyle \sum _{\mathrm{j}}{\mathrm{s}}_{\mathrm{t}\mathrm{o}{\mathrm{n}}_{\mathrm{j}}}({\mathsf{\omega }}_{\mathrm{t}\mathrm{o}{\mathrm{n}}_{\mathrm{j}}},{\mathrm{v}}_{\mathrm{o}},{\mathsf{\nu }}_{\mathrm{v}},\mathrm{t})}\right],\\ \mathrm{t}\in (\mathrm{T}\mathrm{p}],\end{array}$$

(3)

where ${\mathrm{k}}_{\mathrm{n}}(\mathrm{t})$ is the variation function of airframe parameters, which affects its resonant frequencies and modulates the tone signal ${\mathrm{s}}_{\mathrm{t}\mathrm{o}{\mathrm{n}}_{\mathrm{j}}}{(}^{*})$; ${\mathrm{v}}_{\mathrm{o}}$ is the aircraft speed; and ${\mathrm{v}}_{\mathrm{v}}$ is the wind speed.

Signals of industrial noise, including aircraft noise, do not belong to the space described by the models of favorable signals (1, 2) and are not identified in the Wernicke area of the central nervous system. As a result, the otoacoustic emission signal does not compensate for vibrations of the main membrane of the inner ear, and psychophysiological identification processes occur continuously, which causes premature fatigue and destructive changes in the physiological organs of hearing. Constant circulation of perilymph in the cochlea of the inner ear affects the function of semicircular canal receptors, which disrupts the coordination of human’s movements and their sense of balance.

The noise properties of a signal are affected by the modulation law (2) of its tonal (frequency) components. Tone signals of constant frequency with unit index of amplitude modulation are identified by the CNS as a pure tone and cannot be detected as unfavorable. Such signals, during the bench testing of GTEs, include all tone components of signals of the engine components rotating with constant circular frequency.

3. Error Analysis of Method for Assessing Tone Components

To assess errors in the method proposed by the ICAO (1), let us analyze the adequacy of its application [9] when assessing the presence of tone components in noise signals.

The ICAO methodology uses the most common and intuitive method of spectral analysis. Considering the requirements and limitations affecting the [10] the function $\mathrm{s}(\mathrm{t})$ of spectral methods, we conduct we conduct a theoretical analysis of the correspondence of the characteristics and parameters of a GTEs noise signal.

To apply the spectral method in [1], model (3) was simplified to a spectral model by excluding the functional relation of the noise signal components and dynamic parameters of the aircraft and introducing random changes in the value and direction of its speed vector (4):

$$\begin{array}{l}\mathrm{s}(\mathsf{\omega },\mathrm{t})={\displaystyle \sum _{\mathrm{j}}{\mathrm{A}}_{\mathrm{j}}(\mathrm{t})\exp (-\mathrm{j}{\mathsf{\omega }}_{\mathrm{j}}\mathrm{t})},\\ \mathrm{t}\in [\mathrm{T}\mathrm{p}],\\ \mathsf{\omega }\in [\Delta \mathsf{\Omega }],\Delta \mathsf{\Omega }=(100–\mathrm{10,000})\mathrm{H}\mathrm{z}\end{array}$$

(4)

Therefore, it is assumed that if the hypothesis about the local constancy of tone signal parameters is accepted at the time interval $\mathrm{T}\mathrm{p}$ of the analysis, the probability density distribution function of the noise signal amplitudes $\mathrm{A}(\mathrm{t})$ is deterministic and follows the normal law of distribution. In the ICAO methodology [1], there are no requirements for determining the “quasi-stationarity” of model signals (4), so the application of the spectral analysis method is not strictly substantiated.

The spectral mathematical model is based on the method of reversible signal transformations $\mathrm{s}(\mathrm{t})$ using a system of orthogonal functions. The main advantage of such transformations is that they allow the noise signal to be represented as a finite sum $\mathrm{j}$ of independent deterministic components $\mathrm{s}(\mathrm{t})={\displaystyle \sum _{\mathrm{j}}{\mathrm{a}}_{\mathrm{j}}{\mathsf{\psi }}_{\mathrm{j}}(\mathrm{t})}$.

The modern spectral approach contains two main ideas: the synthesis and analysis of information and identification components of noise (relatively to an engine component). Spectral signal synthesis is understood to be to be the process of information generation by engine parts of deterministic orthogonal components ${\mathrm{a}}_{\mathrm{j}}{\mathsf{\psi }}_{\mathrm{j}}(\mathrm{t})$ with their spatial summation in the far diffusion field. A number $\mathrm{j}$ of orthogonal components and the values of their weighting coefficients ${\mathrm{a}}_{\mathrm{j}}$ authenticate information and identification components. Spectral analysis, accordingly, refers to the process of information decomposition of a signal $\mathrm{s}(\mathrm{t})$ into orthogonal components ${\mathrm{a}}_{\mathrm{j}}{\mathsf{\psi }}_{\mathrm{j}}(\mathrm{t})$ with their subsequent information processing.

The system of complex exponential functions is most widely used in spectral analysis. With known expressions of basis functions ${\mathsf{\psi }}_{\mathrm{j}}(\mathrm{t})=\exp (-\mathrm{j}{\mathsf{\omega }}_{\mathrm{j}}\mathrm{t})$, the signal $\mathrm{s}(\mathrm{t})$ is uniquely determined by a set of coefficients ${\mathrm{a}}_{\mathrm{j}}$ and can be restored from these coefficients with any ($\mathrm{j}\to \infty$) degree of accuracy. Thus, any stationary function of a Hilbert space can be represented as a complex Fourier series, which is fundamental for spectral models (4). In practice, a Fourier series is limited to a definite number of $\mathrm{j}$ terms. Limiting the number of terms in the series means the approximation of an infinite-dimensional signal by the $\mathrm{j}$-dimensional system of basis functions of the signal spectrum with a certain methodological error depending on the actual spectrum of the signal.

Limiting the summation of interval $\mathrm{t}\in [\mathrm{T}\mathrm{p}]$ through the quasi-stationarity time of parameters leads to additional errors (in line with the above), which affect information adequacy. In addition, trigonometric (and related complex potential) functions are eigenfunctions (deterministic on the integration interval $\mathrm{T}\mathrm{p}$) and are therefore suitable for studying the information characteristics and parameters of signals, for which there are no changes in parameters over time ($\mathrm{A}(\mathrm{t})=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$ and $\mathsf{\omega }(\mathrm{t})=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$ (4), i.e., deterministic).

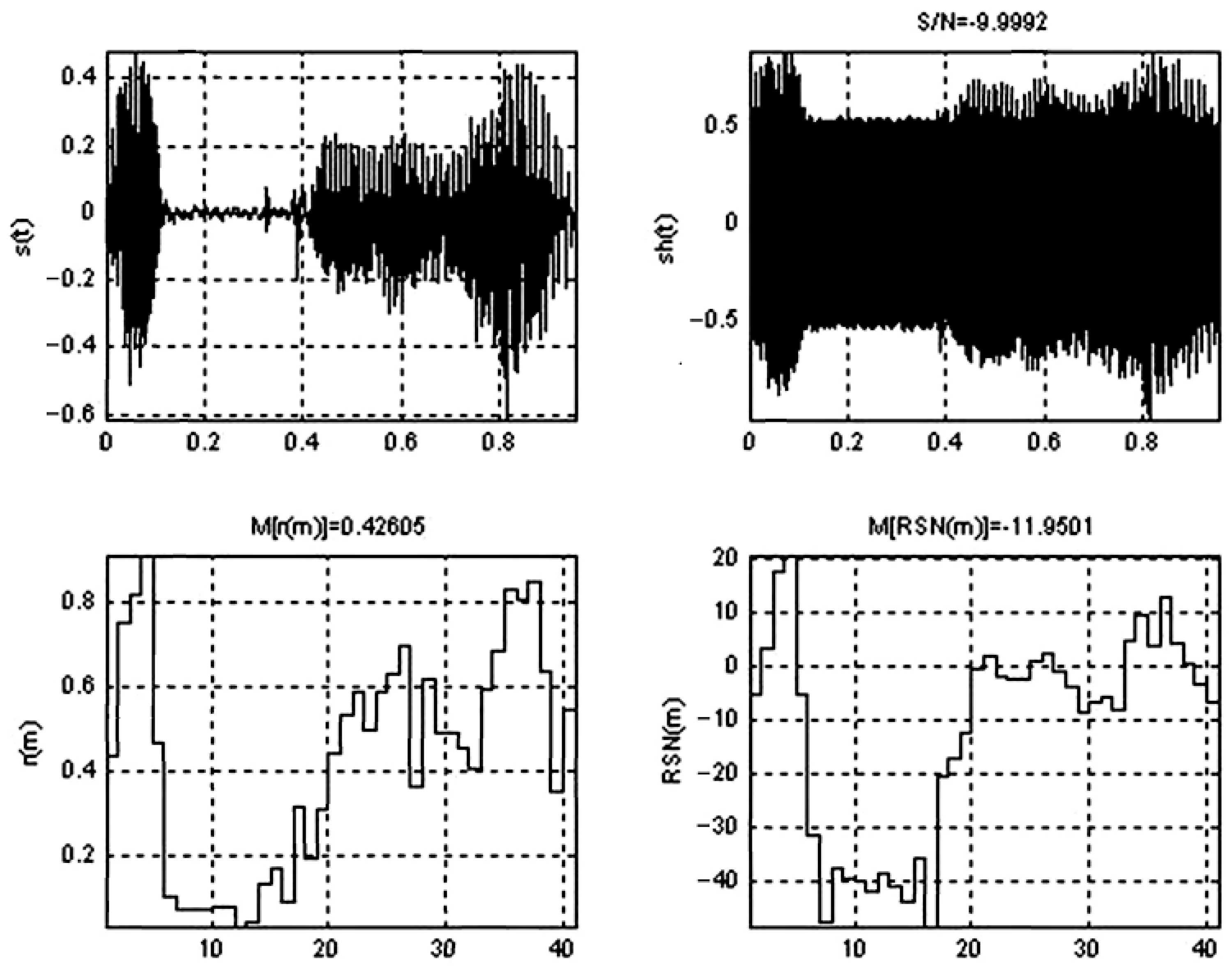
Figure 2 shows a fragment of a graph of the sound pressure of the noise signal recorded in the interval of analysis time in the front hemisphere of a D-18T (Figure 3) turbojet bypass engine at the bench testing stage. The engine was developed by Ivchenko-Progress SE and used for the heavy transport aircraft An-124 and An-225. Visual assessment of the deviation of amplitudes $\mathrm{A}(\mathrm{t})$ in the analysis time interval $\mathrm{T}\mathrm{p}=55\mathrm{s}$ shows a discrepancy in the signal parameters and the stationarity criteria.

The resolution of localizing amplitudes and frequencies using the using the spectral method is determined by the Heisenberg uncertainty principle. This means that it is impossible to obtain an arbitrarily accurate time–frequency representation of the signal, i.e., it is impossible to determine, for any point in time, which spectral components are present in the signal. The smaller the $\mathrm{T}\mathrm{p}$ analysis window, the better the time resolution and the worse frequency resolution, and vice versa. In addition, the smaller the window, the more rigorous our assumptions about the stationarity of the signal within the window become.

Through a prism of analyzing the signal (Figure 2) in the frequency domain and accurately restoring it after transformations, we can note the disadvantages of decomposing signals into Fourier series; we emphasize the main ones below [11]:

-

There is limited information on the analysis of non-stationary time intervals and an almost complete absence of possibilities for analyzing the parameters of signal features (singularities), because in the frequency domain, “blurring” of signal features (breaks, steps, peaks, etc.) occurs both across the analysis window and across the entire frequency range of the spectrum.

-

Deterministic trigonometric eigenbasis functions of the expansion ${\mathsf{\psi }}_{\mathrm{j}}(\mathrm{t})=\exp (-\mathrm{j}{\mathsf{\omega }}_{\mathrm{j}}\mathrm{t})$ are not capable of representing signal differences with an infinite slope of parameter change, because this requires an infinitely large number of terms of the series. When the number of terms of the Fourier series is limited, oscillations arise in the vicinity of jumps and there are discontinuities in the reconstructed signal (Gibbs effect).

Thus, the use of the spectral analysis method for GTE noise signals, for which the stationarity parameters in the diffusion far field are not determined, leads to an uncertain systematic error, which is not taken into account in the ICAO methodology [1]. Determining the tonality value, which determines the correction of deterioration of the engine noise assessment, is not rigorously substantiated and is random in nature.

In accordance with the above analysis, in our opinion, it is necessary to adjust the traditional methods of the environmental certification of aircraft in terms of noise level. The methodology should involve the identification of neutral (the total parameter is not adjusted), unfavorable (the total parameter is adjusted towards worsening) and favorable (the overall parameter is adjusted towards improvement) signals. The ranking algorithm can be intelligent and function identically Wernicke center of the human central nervous system [12]. It can be implemented by calculating the cross-correlation function or the correlation coefficient of the aircraft noise signal with the signals from the database of “favorable” or “unfavorable” signals.

4. Conclusions

A psychophysiological analysis of the methodology for applying tonality correction during bench tests of gas turbine engines for compliance with ICAO noise requirements was carried out [1]. Based on the results of the analysis, the following conclusions can be drawn.

• The environmental properties of the signal are influenced by the modulation law (2) of its tonal components. Tone signals of constant frequency with a unit amplitude modulation index are identified by the central nervous system as a pure tone and cannot be defined as unfavorable. Such signals during bench tests of gas turbine engines include all tone components of signals from engine parts rotating at a constant circular frequency.
• The use of the spectral analysis model (4) for signals, for which the stationarity parameters in the diffusion far field are not determined, leads to an uncertain systematic error, which is not taken into account in the ICAO method [1]. Determining the tonality value, which determines the correction of deterioration of the engine noise assessment, is not rigorously substantiated and is random in nature.

Ivchenko-Progress SE proposed a method for the psychophysiological ranking of GTE noise signals, which assumes an intellectual algorithm of signal processing corresponding to the function of the speech zones of the human central nervous system.

Taking into account additional studies of different demographic groups of the population, the proposed method will allow for a more objective analysis of the impact of aircraft noise on the environment and the physiological human state.