PSO-Based PID Tuning for PMSM-Quadrotor UAV System ^†

Abstract

This paper presents the simulation and controller optimization of a quadrotor Unmanned Aerial Vehicle (UAV) system. The quadrotor model is derived adopting the Newton-Euler approach, and is intended to be constituted by four three-phase Permanent Magnet Synchronous Motors (PMSM) controlled with a velocity control loop-based Field Oriented Control (FOC) technique. The Particle Swarm Optimization (PSO) algorithm is used to tune the parameters of the PID controllers of quadrotor height, quadrotor attitude angles, and PMSMs’ rotational speeds, which represent the eight critical parameters of the PMSM-quadrotor UAV system. The PSO algorithm is designed to optimize eight Square Error (SE) cost functions which quantify the error dynamics of the controlled variables. For each stabilization task, the PID tuning is divided in two phases. Firstly, the PSO optimizes the error dynamics of altitude and attitude angles of the quadrotor UAV. Secondly, the desired steady-state rotational speeds of the PMSMs are derived, and the PSO is used to optimize the motors’ dynamics. Finally, the complete PMSM-Quadrotor UAV system is simulated for stabilization during the target task. The study is carried out by means of simulations in MATLAB/Simulink^®.

1. Introduction

Urban Air Mobility (UAM) represents a promising innovation in the field of urban transportation, and nowadays is seen as a potential revolution in the context of smart cities. In particular, Unmanned Aerial Vehicles (UAVs), as a key element of UAM, are suitable for a variety of applications and missions spanning from surveillance to passenger transportation [1]. For instance, in the delivery sector, UAVs can reduce delivery times and costs while minimizing the environmental impact with respect to the traditional truck-based delivery [2,3,4,5,6,7].

Quadrotors are widely recognized as the most promising configuration among all the types of UAVs, mainly for their maneuverability, relatively low cost, and capability to perform almost any type of task [8]. Quadrotor UAVs are flying mechatronic systems equipped with propellers, motors, electronic speed controllers, and different kinds of payloads (sensors, battery, CPU, etc.) integrated into their cross-shaped structure. Among brushless motors, Permanent Magnet Synchronous Motors (PMSMs) are remarkably dependable and efficient. Without compromising the torque generation capability, PMSMs can help reduce the size of the platform thanks to their power-to-size ratio [9]. PMSMs enhance UAV control by generating high thrust, thus improving maneuverability.

This paper investigates the performance of a quadrotor equipped with four PMSMs, focusing on its dynamics during hovering and maneuvering. Controlling UAVs with PMSMs involves controlling the motors’ speed to control the drone’s direction, this is typically achieved with a series of decentralized Proportional-Integral-Derivative (PID) controllers. To further optimize the performance of the closed-loop system, a Particle Swarm Optimization (PSO) algorithm is designed to tune the parameters of each PID controller. Several works can be found in the literature about the tuning of PID controllers of quadrotors with PSO algorithms for attitude control and trajectory tracking [10,11,12,13,14,15], but the inclusion of the motor dynamics in the loop is unseen (a part from simplifications with first order motor’s dynamics) even though it is crucial for the development of the drone digital twin [16]. By exploiting the PSO algorithm for the optimal tuning of all the PID controllers of the system, it is possible to comprehensively simulate the PMSM-Quadrotor UAV system and optimize the performances.

2. Methodology

This section presents the methodology adopted for the development of this work, which is composed by (i) the model of the quadrotor UAV based on the Newton-Euler formalism, (ii) the model of the PMSMs, (iii) the control model of the PMSM-Quadrotor UAV system by means of PID control, and (iv) the PSO algorithm for the optimal tuning of the PID parameters. The simulation settings are also presented for the sake of repeatability of the results.

2.1. System Model

Figure 1 shows a schematic representation of the two systems simulated in this work, i.e., the quadrotor platform and the PMSM.

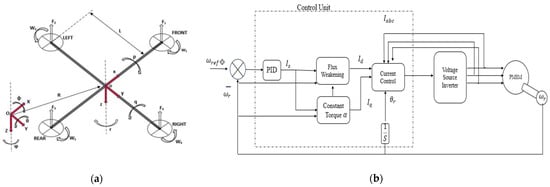
Figure 1. (a) Schematic representation of the quadrotor platform, taken from [17]. (b)Schematic representation of the PMSM system and its control unit.

2.1.1. Quadrotor UAV Model

The nonlinear dynamical model of the quadrotor UAV adopted in this work is based on the Newton-Euler formalism. Such model, as reported in Equation (1), is the same model developed in one of our previous works [17]. Refer to [17] for the complete terminology as well as the assumptions.

$$\begin{array}{c}Zˋ̀=g-{\displaystyle \frac{1}{m}}{K}_d^{L}Z`-{\displaystyle \frac{1}{m}}{c}_{\theta }{c}_{\varphi }{U}_1\\ p`={\displaystyle \frac{I_Y-I_z}{I_x}}qr-{\displaystyle \frac{I_R}{I_x}}qf\left(\mathit{u}\right)-{\displaystyle \frac{1}{I_x}}{K}_d^{R}p+{\displaystyle \frac{1}{I_x}}L{U}_2\\ q`={\displaystyle \frac{I_z-I_x}{I_y}}pr-{\displaystyle \frac{I_R}{I_y}}pf\left(\mathit{u}\right)-{\displaystyle \frac{1}{I_y}}{K}_d^{R}q+{\displaystyle \frac{1}{I_y}}L{U}_3\\ r`={\displaystyle \frac{I_x-I_y}{I_z}}pq-{\displaystyle \frac{1}{I_z}}{K}_d^{R}r+{\displaystyle \frac{1}{I_z}}{U}_4\\ \varphi `=p+s_{\varphi }{s}_{\theta }{c}_{\theta }^{-1}q+c_{\varphi }{s}_{\theta }{c}_{\theta }^{-1}r\\ \theta `=c_{\varphi }q-s_{\varphi }r\\ \psi `=s_{\varphi }{c}_{\theta }^{-1}q+c_{\theta }^{-1}{c}_{\varphi }r\\ f\left(\mathit{u}\right)={\sum }_{i=1}^4{\left(-1\right)}^{i+1}\sqrt{\left|{(M_{bd}}^{-1}{\mathit{u})}_i\right|}=w_1+w_3-w_2-w_4\\ \mathit{u}=\left(\begin{array}{c}{U}_1\\ U_2\\ U_3\\ U_4\end{array}\right)=M_{bd}{\mathit{w}}^2=\left(\begin{array}{cccc}b& b& b& b\\ 0& b& 0& -b\\ b& 0& -b& 0\\ d& -d& d& -d\end{array}\right)\left(\begin{array}{c}{w}_1^2\\ w_2^2\\ w_3^2\\ w_4^2\end{array}\right)\end{array}$$

(1)

2.1.2. PMSM Model

A Permanent Magnet Synchronous Motor (PMSM) operates with a rotor made of permanent magnets and a stator with three-phase windings, synchronizing its speed with the AC power frequency. A Voltage Source Inverter (VSI) provides the necessary AC power, while a control unit adjusts the motor’s stator currents for optimal performance. The motor operates in constant torque mode up to its rated speed, and switches to flux weakening mode for higher speeds by reducing the d-axis current, allowing for extended speed ranges while maintaining efficiency. The d-q model is developed in the rotor reference frame, where at any time $t$, the rotor d-axis (rotating at the same speed of the rotor) forms an angle ${\theta }_r$ with the fixed stator phase axis. The voltage equations are reported in Equation (2).

$$\begin{array}{c}{V}_q=R_s{i}_q+{\omega }_r(L_d{i}_d+{\lambda }_f)+\rho \left(L_q{i}_q\right)\\ V_d=R_s{i}_d-{\omega }_r{L}_q{i}_q+\rho (L_d{i}_d+{\lambda }_f)\end{array}$$

(2)

$R_s$ is the stator resistance, ${\omega }_r$ is rotor angular velocity, $L_d$and $L_q$ are dq-axes inductances, ${\lambda }_f$ is flux linkage, $I_d$ and $I_q$ are d-axis and q-axis currents, respectively, and ρ is the derivative operator. The mechanical torque is defined follows:

$$T_e=T_L+B{\omega }_m+J\rho \left({\omega }_m\right)$$

(3)

with $T_e$ being the developed torque, $T_L$ the load torque, $B$ the viscous friction coefficient, $J$ the rotor inertia. The rotor mechanical speed is reported in Equation (4).

$${\omega }_m={\omega }_r\left({\displaystyle \frac{2}{P}}\right)$$

(4)

where ${\omega }_r$ is the rotor electrical speed, ${\omega }_m$ is the rotor mechanical speed, and $P$ is the number of poles.

The dynamic d-q modeling technique is utilized to analyze motors under transient and steady-state conditions by transforming three-phase voltages and currents into dq0 variables using the Park transformation. This conversion of $i_{abc}$ to $i_{dq0}$ in the rotor reference frame is expressed by the following equation:

$$⌈\begin{array}{c}{i}_d\\ i_q\\ i_0\end{array}⌉={\displaystyle \frac{2}{3}}\left[\begin{array}{ccc}{cos\theta }_r& {cos(\theta }_r-120°)& {cos(\theta }_r+120°)\\ {sin\theta }_r& {sin(\theta }_r-120°)& {sin(\theta }_r+120°)\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\end{array}\right]⌈\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}⌉$$

(5)

The control of PMSMs mirrors the one of DC motors through Field-Oriented Control (FOC), also known as vector control. This technique decouples torque and flux components of current by modulating the stator excitation. The vector control strategy is derived from the dynamic model of PMSM, utilizing currents as inputs to evaluate the three-phase currents as reported in Equation (6).

$$⌈\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}⌉=\left[\begin{array}{c}cos\left({\omega }_{r}t+\alpha \right)\\ cos\left({\omega }_{r}t+\alpha -{\displaystyle \frac{2\pi }{3}}\right)\\ cos\left({\omega }_{r}t+\alpha +{\displaystyle \frac{2\pi }{3}}\right)\end{array}\right]I_m$$

(6)

where $\alpha$ is the angle between the rotor field and stator current phasor, and $I_m$ is the magnitude of the supply current in d-q reference frame. Stator currents are converted to the rotor reference frame using the Park transformation at rotor speed ${\omega }_r$. In this frame, q- and d- axes currents are constant for a given load torque and considering the angle ${\theta }_r$. The q-axis current acts like the armature current in a DC machine, while the d-axis current represents the field current, partially supplied by the permanent magnet field. Thus, the q-axis current is the torque-producing component, and the d-axis current is the flux-producing component. Manipulation of Equation (6) and Equation (5) yields to:

$$\left[\begin{array}{c}{i}_q\\ i_d\end{array}\right]=I_m\left[\begin{array}{c}Sin\alpha \\ Cos\alpha \end{array}\right]$$

(7)

Finally, the electromagnetic torque $T_e$ is expressed as follows:

$$T_e={\displaystyle \frac{2}{3}}{\displaystyle \frac{P}{2}}\left[{\displaystyle \frac{1}{2}}\left(L_d-L_q\right)I_m^{2}sin2\alpha +{\lambda }_f{I}_{m}sin\alpha \right]$$

(8)

2.2. System Control Model

2.2.1. Quadrotor UAV Control Model

The PID controllers of quadrotor attitude and altitude are defined as:

$$U_i\left(t\right)=K_P^i{e}_i\left(t\right)+K_I^i\int e_i\left(t\right)dt+K_D^i{\displaystyle \frac{d{e}_i\left(t\right)}{dt}}$$

(9)

with $e_i(t)=x_i^{ref}(t)-x_i(t),i=1,\dots ,4$, and ${\left[K_P,K_I,K_D\right]}^i$ to be optimized by the PSO algorithm. In particular, $x=[Z,\varphi ,\theta ,\psi ]$ and $x^{ref}={\left[Z,\varphi ,\theta ,\psi \right]}^{ref}$.

2.2.2. PMSM Control Model

The classical formulation of PID control reported in (9) is applied also to the PMSM speed control system, with the controller being inserted in the speed control loop and computing the reference torque $T_e$ (thus, the reference current) for the motor, as follows:

$$T_e^o\left(t\right)=K_P^o{e}_o\left(t\right)+K_I^o\int e_o\left(t\right)dt+K_D^o{\displaystyle \frac{d{e}_o\left(t\right)}{dt}}$$

(10)

with $e_o(t)=w_o^{ref}(t)-w_o(t),o=1,\dots ,4$. $w$ denotes the motor angular velocity, $w^{ref}$ denotes the reference angular velocity, and ${\left[K_P,K_I,K_D\right]}^o$ is meant to be optimized by the PSO algorithm.

2.3. PSO Algorithm

The Particle Swarm Optimization (PSO) algorithm is based on a swarm of particles learning from each other’s best performances, emphasizing cooperation and competition [18]. Analogous to birds searching for food, each particle adjusts its direction and velocity based on its position and collective insights, iteratively refining their movement until the optimal solution is found.

A swarm consists of multiple particles, each representing a potential solution $x_i$ to an optimization problem. For $D$ parameters, a particle’s position is $x_i=\left(x_{i1},x_{i2},\dots ,x_{iD}\right),$ and the swarm of $N$ particles is $X=(x_1,x_2,\dots ,x_N)$. Each particle updates its position $x_i$ and velocity $v_i$ iteratively. The velocity update equation is defined as follows:

$$v_i^{t+1}=\omega v_i^t+2R_1\left(p_i-x_i^t\right)+2R_2(g-x_i^t)$$

(11)

where $\omega$ is the inertia weight, $R_1$ is the cognitive weight, $R_2$ is the social weight, $p_i$ is the best position of particle $i$ (cognitive component), and $g$ is global best position of the swarm (social component). Therefore, the new position is defined as follows:

$$x_i^{t+1}=x_i^t+v_i^{t+1}$$

(12)

This process continues until convergence, balancing exploration (searching new areas of the search space) and exploitation (refining known good areas). The inertia, cognitive, and social components ensure diverse search behavior, with $R_1=R_2=w$ typically used to balance their influence. The fundamentals of the PSO algorithm and how it is applied to the decoupled systems considered in this work are shown in Figure 2.

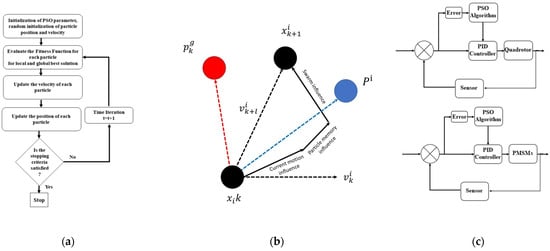
Figure 2. (a) Flow chart of the PSO algorithm based on [19]; (b) Process of searching for a new position in the PSO methodology; (c) Schematic representation of how the PSO framework is used for optimizing the PID parameters of both quadrotor and PMSMs’ controllers.

2.4. Implementing the PSO Approach

The PSO algorithm is utilized to derive the optimal values of the parameters of the PID controller, with the objective of minimizing the discrepancy between desired and simulated dynamics derived from MATLAB/Simulink simulations. The algorithm’s parameters values are specified in Table 1. Leveraging the swarm initialization and the predefined parameter ranges outlined in Table 1, the fitness function is computed to evaluate the performance of each particle. As depicted in Figure 2a, the PSO process starts with the initialization of PSO parameters, including random initialization of particle positions and velocities. Subsequently, the error between the desired and simulated results is evaluated (process represented in Figure 2c. The particles’ velocities and positions are then updated based on Equations (11) and (12). Figure 2b provides a schematic representation of how particles adjust their positions according to individual and global best values. This iterative process of fitness evaluation, velocity adjustment, and position update continues for a predefined number of iterations or until a convergence criteria are met, such as achieving minimal changes in the global best value $g$. As shown in Figure 2c, this process ensures the determination of optimal parameters for both quadrotor and PMSMs’ PID controllers.

Table 1. Initial parameter for PSO algorithm.

Optimization Algorithm	Parameter	Value
PSO	Number of Variables	16
	Limitation of Border	[0.1, 1000]
	Maximum Number of Iterations	5
	Population Size	8
	Inertia Coefficient	1
	Damping Ratio of Inner Coefficient	0.99

2.5. Simulation Settings

Both the PMSM-Quadrotor UAV system and the PSO algorithm are implemented in MATLAB/Simulink. The parameters of the quadrotor model are the same as the ones reported in our previous work in [17]. The characteristics of the PMSM model are defined in Table 2.

Table 2. Characteristics of the PMSM model.

PMSM Parameter	Value/Type
Phase Number	3
Back EMF Waveform	Sinusoidal
Rotor Type	Round
Mechanical Input	Torque
Stator Phase Resistance	$2.875\mathsf{\Omega }$
Armature Inductance	$0.00153\mathrm{H}$
Flux Linkage	$0.175\mathrm{W}\mathrm{b}$
Rotor Inertia	$8\times {10}^{-4}\mathrm{k}\mathrm{g}·{\mathrm{m}}^2$

3. Simulation Results

In this section the simulation results are presented. The optimization of the PID parameters’ values is decoupled in two stages: (i) the quadrotor altitude and attitude PID controllers are optimized for a stabilization task with the aim to minimize the SE cost function of the error signals’ dynamics, (ii) the reference steady-state rotational speed of each PMSM $i$ ($i=1,\dots ,4$) is computed for that task by means of ${\left(-1\right)}^{i+1}\sqrt{\left|{(M_{bd}}^{-1}{\mathit{u})}_i\right|}$, as in Equation (1), and the PSO is used to optimize the PID speed controllers with the aim to minimize the motors’ error dynamics. The complete PMSM-Quadrotor UAV system is then simulated during hovering and maneuvering tasks, with all the eight PID controllers being optimized by the PSO approach. Figure 3 shows the comparison of the system’s dynamics during stabilization for 2 tasks: hovering and maneuvering, with different random initial conditions. The PMSM-Quadrotor UAV is simulated with the PID controllers of the motor being optimized by the PSO, and the PID controllers of the quadrotor being both optimized (Figure 3a,c) and non-optimized (Figure 3b,d). Reduction of oscillations and superior fastness of response in the attitude and altitude signals are observed for the optimized system.

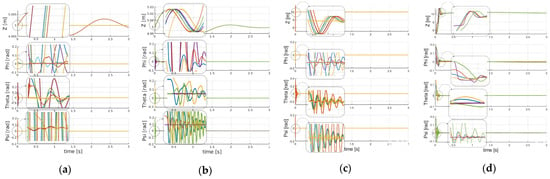
Figure 3. Comparing (a) optimized and (b) non-optimized PMSM-Quadrotor UAV system’s performances for a hovering stabilization task. Comparing (c) optimized and (d) non-optimized PMSM-Quadrotor UAV system’s performances for a maneuvering stabilization task. Simulations performed with a set of random initial conditions.

In Table 3 the cost function values, computed in the simulations shown in Figure 3, referring to the sum of the attitude angles’ SE cost function ($S{E}_{\varphi ,\theta ,\phi }$) are presented, highlighting the significant reduction of the SE when the PID controllers are tuned by the PSO algorithm.

Table 3. Comparison of the SE cost function values ($S{E}_{\varphi ,\theta ,\phi }$) with optimized and non-optimized PID parameters. Simulations performed with 5 random initial conditions for both Hovering (H) and Maneuvering (M) stabilization tasks.

$\mathbf{Squared}\mathbf{Error}\mathbf{Cos}\mathbf{t}\mathbf{Function}\mathbf{Values}\mathbf{of}\mathbf{PMSM-}\mathbf{Quadrotor}\mathbf{UAV}\text{’}\mathbf{s}\mathbf{Attitude}\mathbf{Signals}\left(\mathit{S}{\mathit{E}}_{\mathit{\varphi },\mathit{\theta },\mathit{\phi }}\right)$
Optimized H	Non-Optimized H	Optimized M	Non-Optimized M
$1.487\times 10^{-3}$	$3.369\times 10^{-3}$	$0.054$	$0.0819$
$5.431\times 10^{-4}$	$1.701\times 10^{-3}$	$0.0286$	$0.0687$
$1.298\times 10^{-3}$	$5.015\times 10^{-3}$	$0.0461$	$0.109$
$7.167\times 10^{-4}$	$1.115\times 10^{-3}$	$1.675\times 10^{-3}$	$5.055\times 10^{-3}$
$2.705\times 10^{-3}$	$7.851\times 10^{-3}$	$0.0986$	$0.129$

Figure 4a,b show the optimized dynamics of one motor during one of the maneuvering stabilization tasks of Figure 3. Figure 4c,d show the comparison of the performance of one motor for different reference velocity signals in case of optimized and non-optimized controller. Again, faster dynamics and oscillations reduction are observed due to the PSO optimization of the speed controllers.

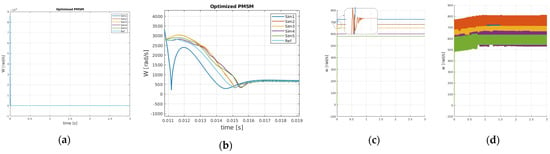
Figure 4. (a,b) Optimized dynamics of one motor during the maneuvering stabilization tasks, simulations refer to the same set of Figure 3c. Comparing (c) optimized and (d) non-optimized dynamics of one motor for different reference velocities (i.e., different maneuvers).

4. Conclusions

This paper presents a simulative study of a PMSM-Quadrotor UAV system with decentralized PID controllers of quadrotor attitude and altitude, and motors’ rotational speed. A PSO algorithm is implemented to optimize the performances in terms of squared error cost functions of the controlled variables’ error dynamics. Simulation results with different initial conditions for both hovering and maneuvering stabilization tasks corroborate the validity of the approach. This work shows how to develop the set of system engineering tools for further advancing the drone digital twins. Future works will be focused on the comparison of the performances obtained by implementing other optimization approaches for tuning the controllers as well as the development of comprehensive simulative studies with different types of quadrotors and motors.