Winglet Design for Class I Mini UAV—Aerodynamic and Performance Optimization †
Abstract
1. Introduction
- Winglets influence the wetted area, thereby impacting viscous drag.
- They alter the wingtip vortex, similarly to the effects of increasing aspect ratio.
- They adjust the spanwise pressure distribution and can be designed to delay the onset of wave drag.
2. Materials and Methods
2.1. Original Aircraft’s Characteristics
2.2. Winglet Design Methodology
2.3. Winglet Configurations
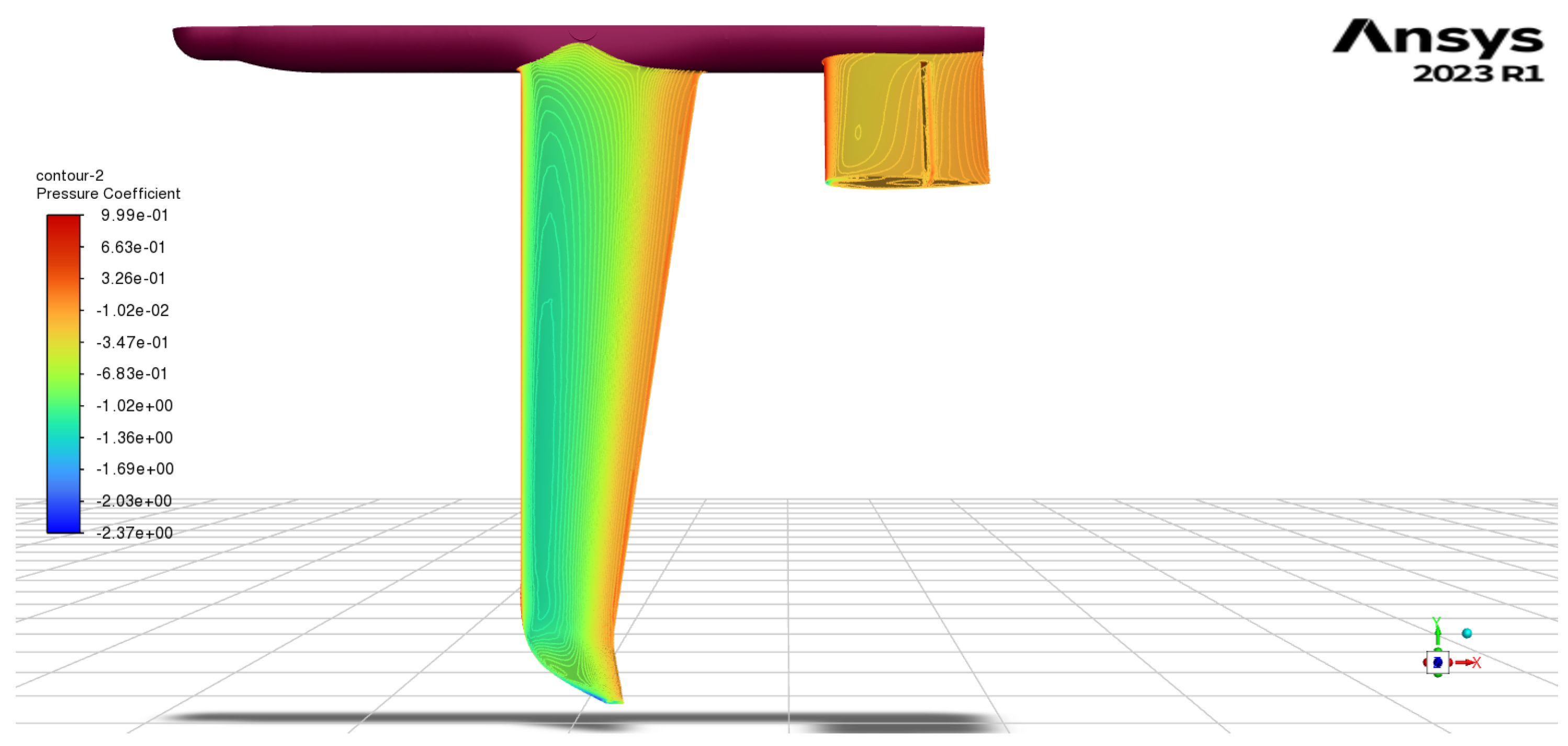
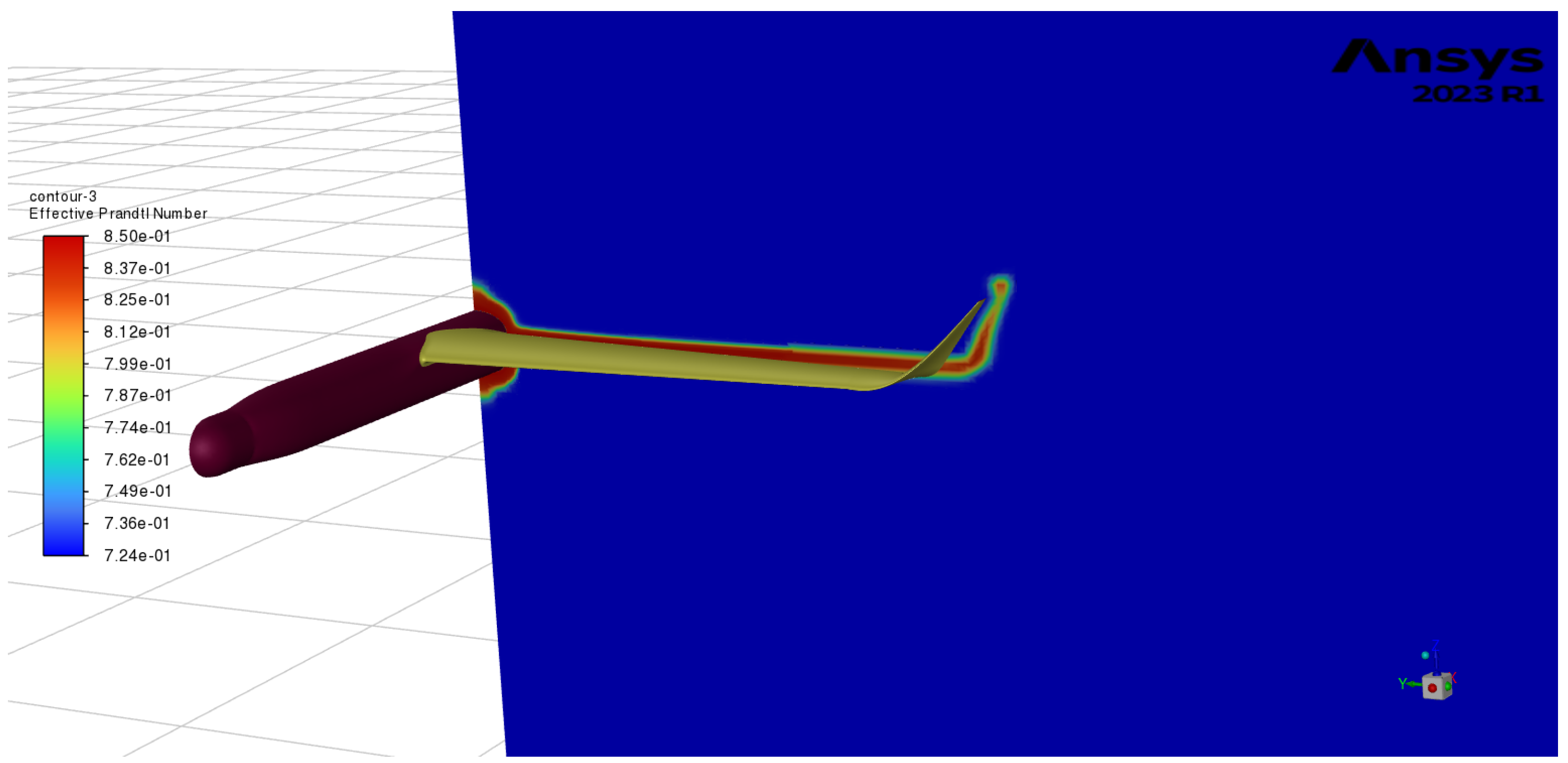
2.4. Computational Fluid Dynamics (CFD)
3. Results
3.1. Aerodynamic Results and Comparison
3.2. Performance Evaluation
3.3. Optimal Configuration
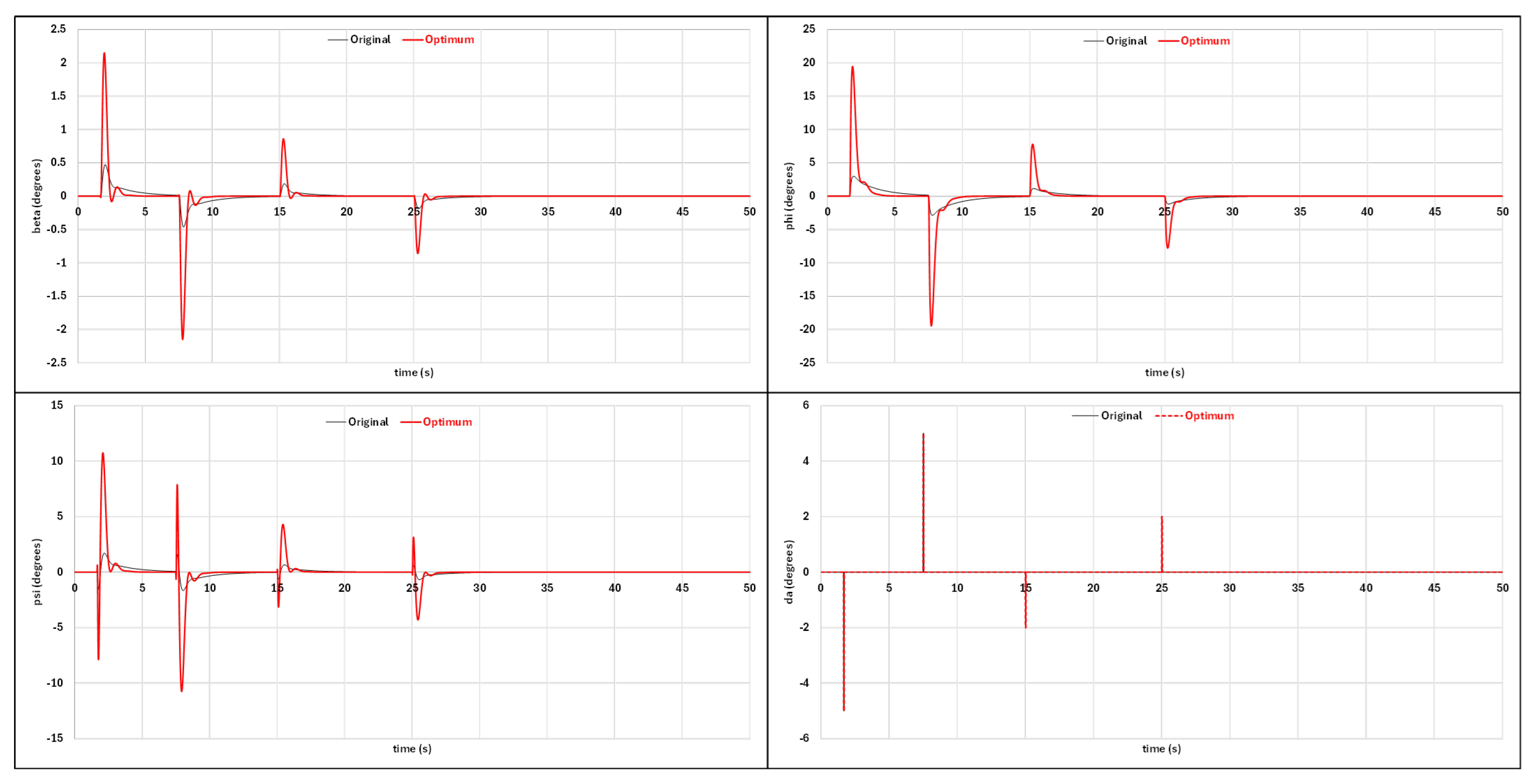
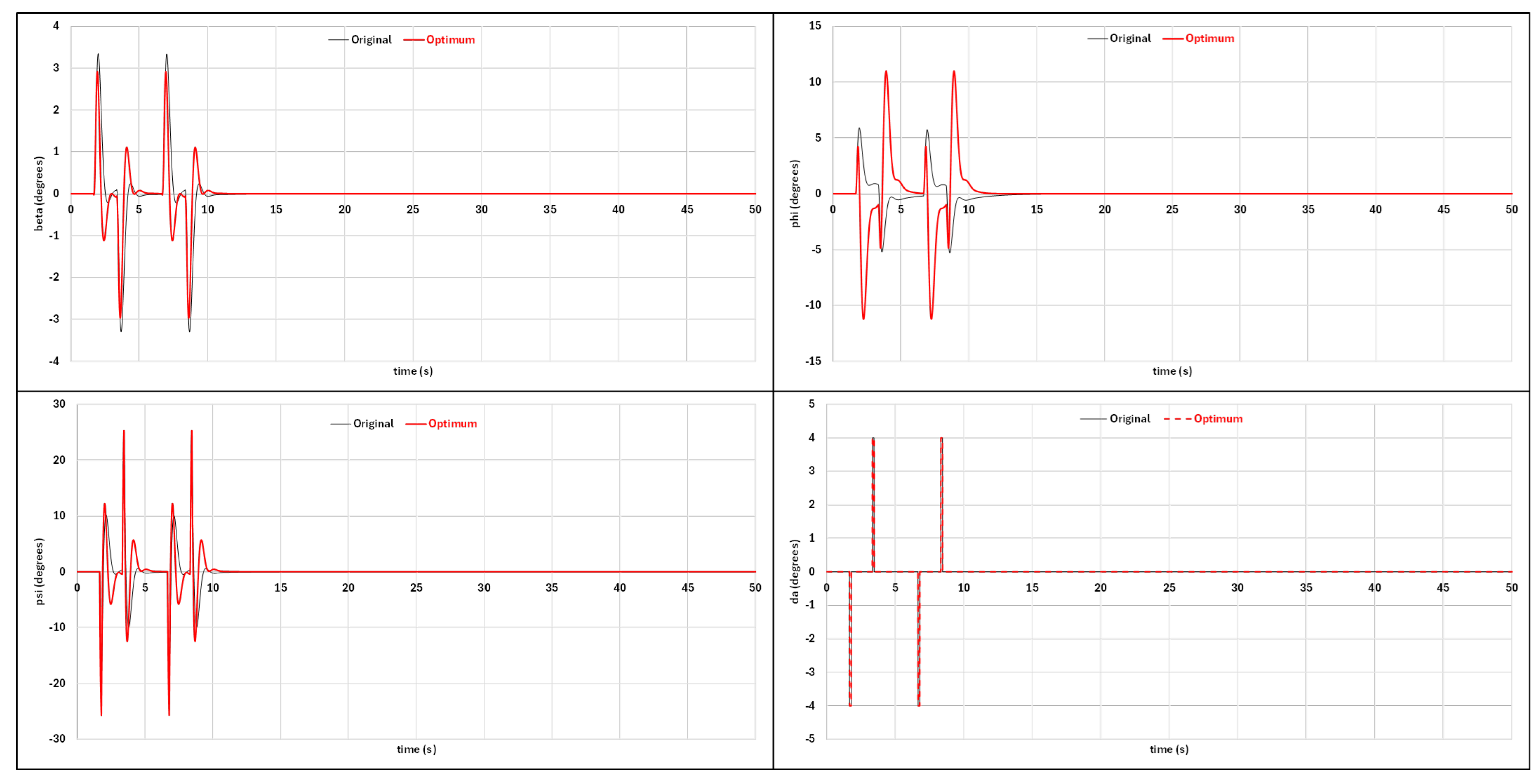
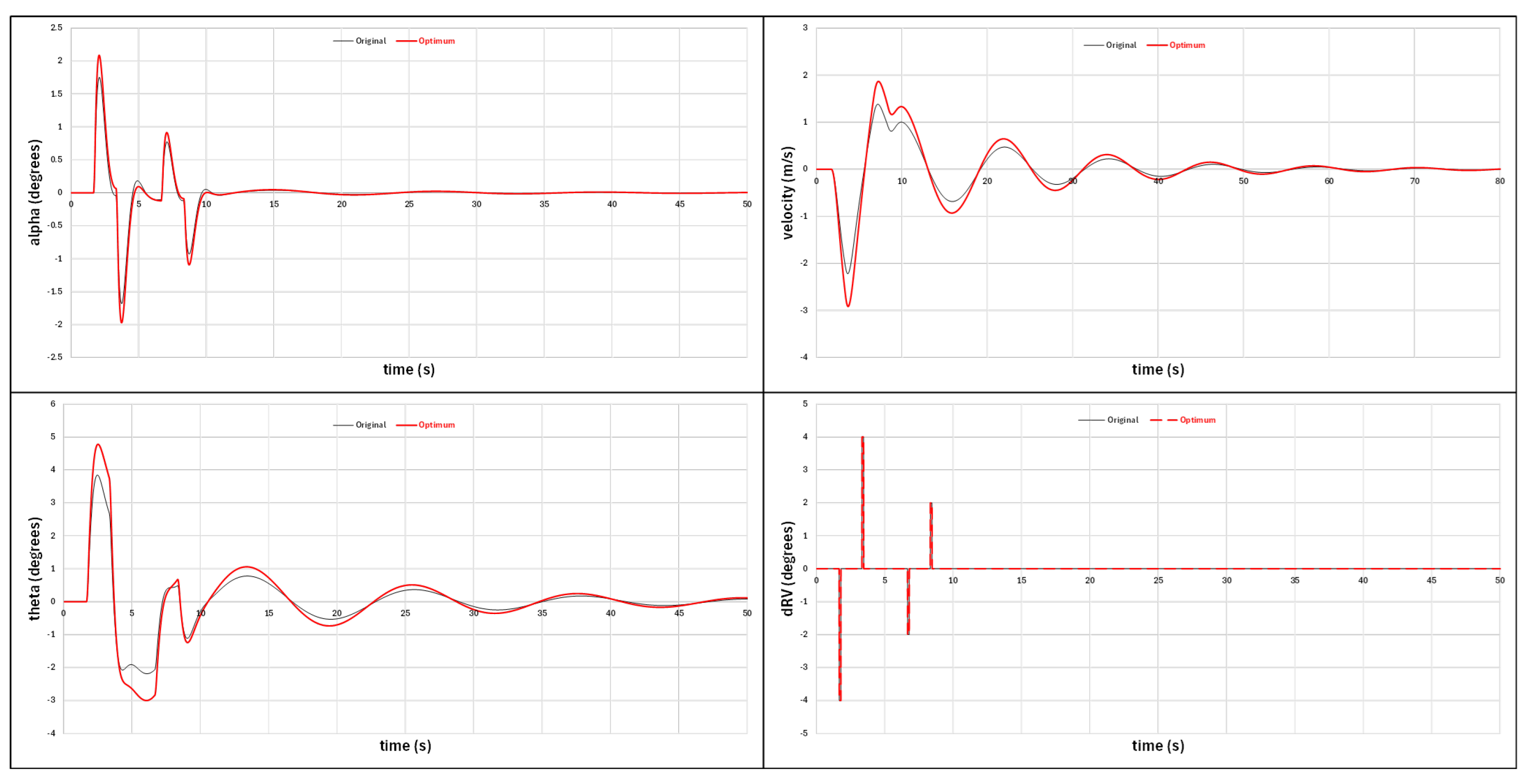
3.4. Stability and Control Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gudmundsson, S. General Aviation Aircraft Design: Applied Methods and Procedures; Butterworth-Heinemann: Oxford, UK, 2021. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 6th ed.; AIAA Education Series; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Whitcomb, R.T. A Design Approach and Selected Wind-Tunnel Results at High Subsonic Speeds for Wing-Tip Mounted Winglets. Technical Report, National Aeronautics and Space Administration. 1976. Available online: https://ntrs.nasa.gov/citations/19760019075 (accessed on 1 March 2025).
- Gratzer, L.B. Blended Winglet. United States Patent No. 5348253, 20 September 1994. [Google Scholar]
- Panagiotou, P.; Kaparos, P.; Yakinthos, K. Winglet design and optimization for a MALE UAV using CFD. Aerosp. Sci. Technol. 2014, 39, 190–205. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, D.; Yang, M.; Wang, S. Optimization and analysis of winglet configuration for solar aircraft. Chin. J. Aeronaut. 2020, 33, 3238–3252. [Google Scholar] [CrossRef]
- Eguea, J.P.; Bravo-Mosquera, P.D.; Catalano, F.M. Camber morphing winglet influence on aircraft drag breakdown and tip vortex structure. Aerosp. Sci. Technol. 2021, 119, 107148. [Google Scholar] [CrossRef]
- Utomo, M.T.S.; Yohana, E.; Mahendra, C.; Utama, I.Y. Analysis of blended winglet parameters on the aerodynamic characteristics of NXXX aircraft using Computational Fluid Dynamics (CFD). Results Eng. 2024, 24, 102901. [Google Scholar] [CrossRef]
- Roskam, J.; Lan, C. Airplane Aerodynamics and Performance; Airplane design and analysis, Roskam Aviation and Engineering; Darcorporation: Lawrence, KS, USA, 1997. [Google Scholar]

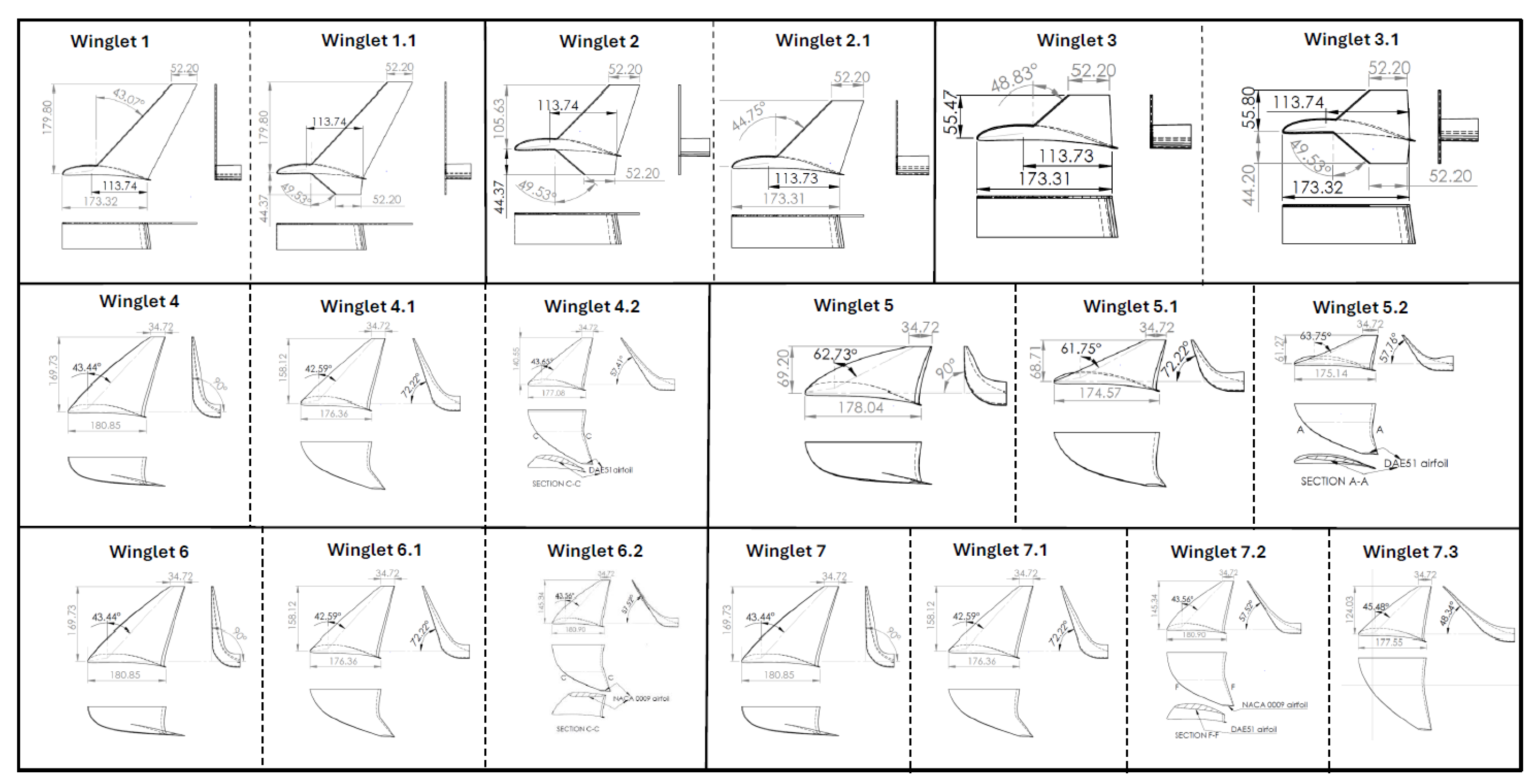
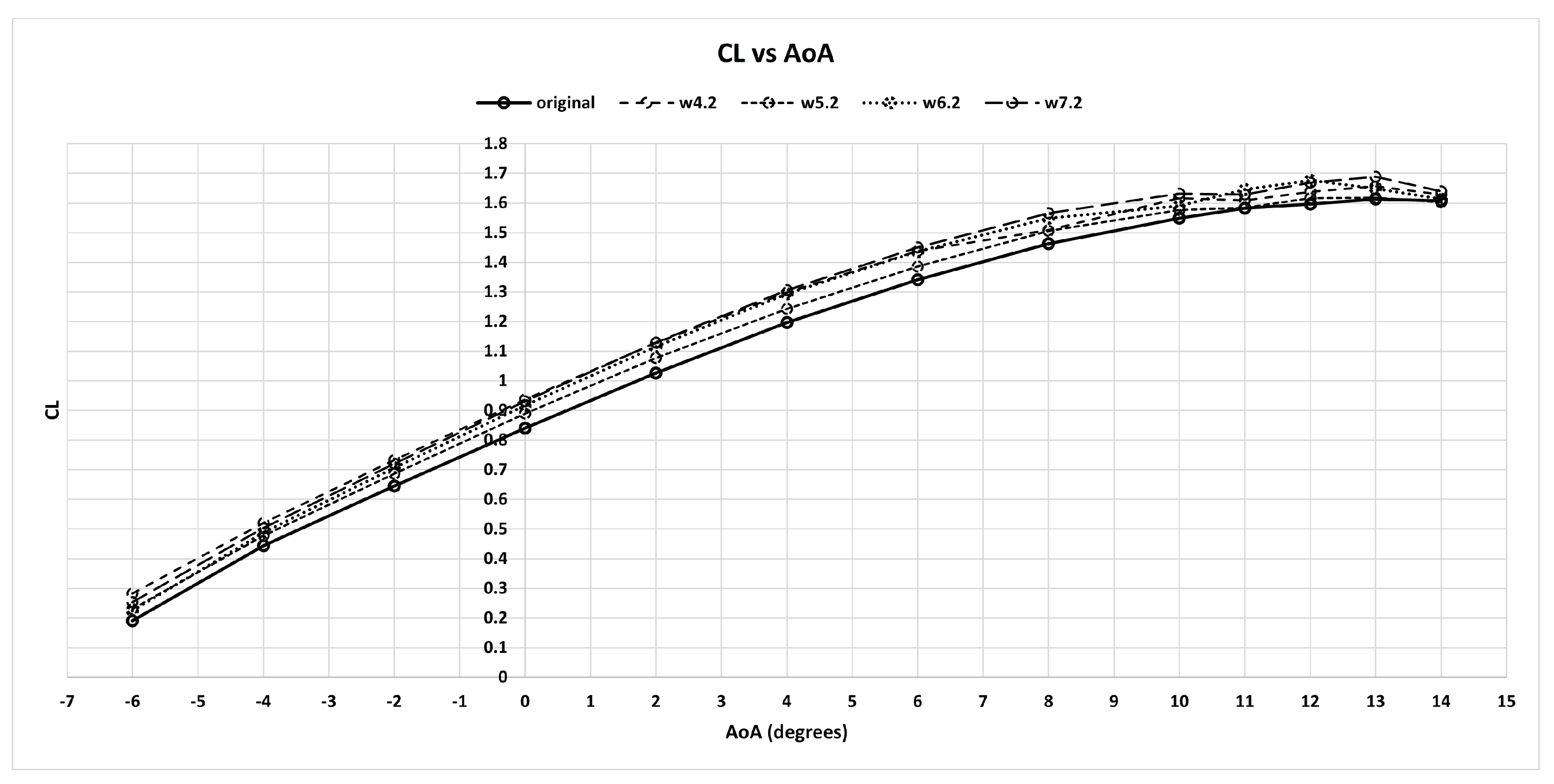
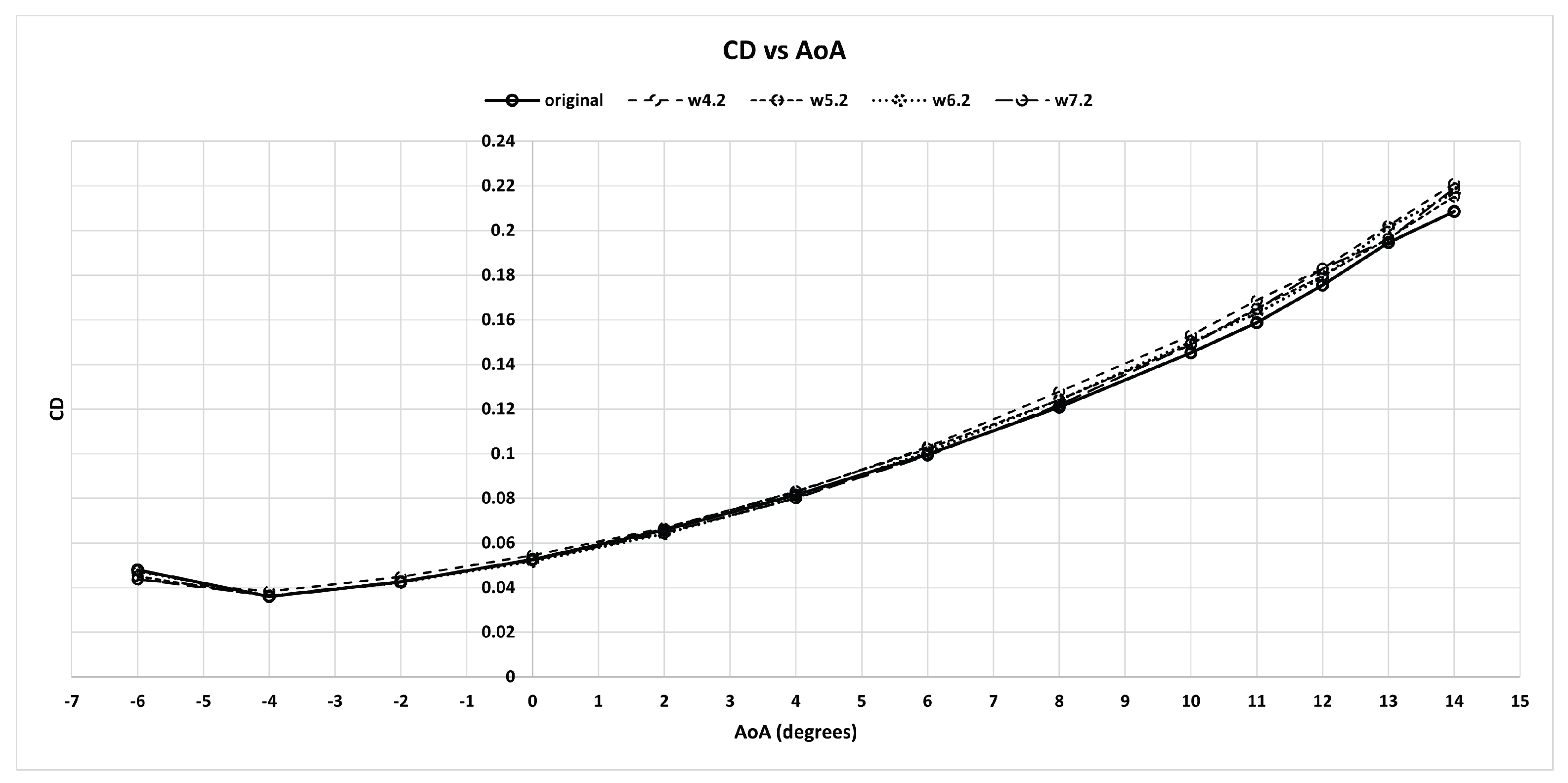

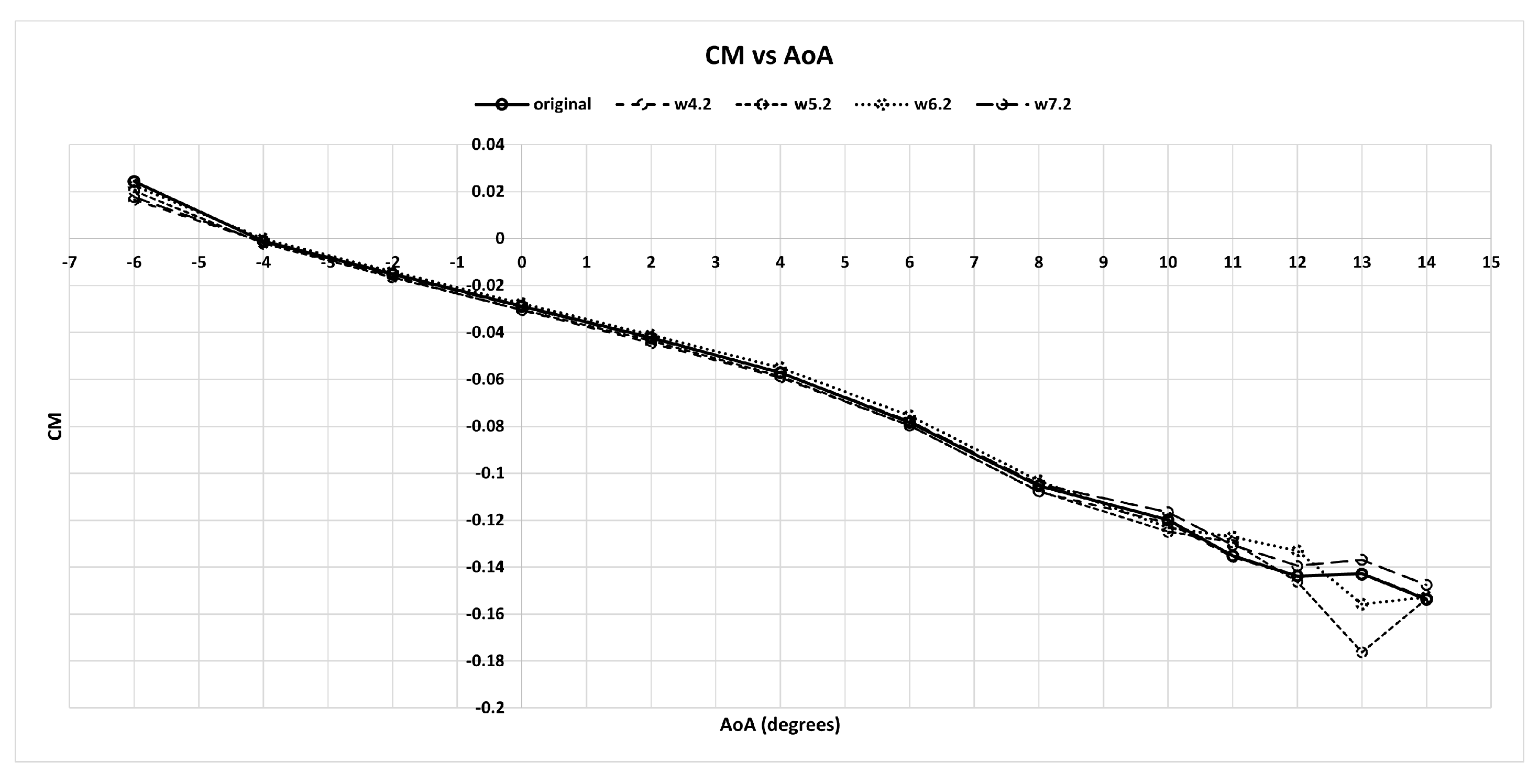




| Characteristic | Symbol | Value |
|---|---|---|
| Take-off weight (kg) | 14.3 | |
| Wing Area (m2) | 0.6 | |
| Wingspan (m) | 2.3 | |
| UAV length (m) | l | 1.6 |
| Wing Aspect Ratio | AR | 8.8 |
| Wing Taper Ratio | 0.5 | |
| Wing root chord (m) | 0.375 | |
| Battery mass (kg) | 2.6 | |
| Battery Spec. Energy (kW/kg) | 145 | |
| Total system efficiency (battery to motor output shaft) | 0.9114 | |
| Propeller efficiency | 0.785 |
| A/A | Config. | ||||||
|---|---|---|---|---|---|---|---|
| 1 | Original | 1.6133 | 0.0360 | 15.9440 | - | - | - |
| 2 | W1 | 1.6190 | 0.0369 | 16.1521 | 0.35% | 2.46% | 1.29% |
| 3 | W1.1 | 1.6198 | 0.0369 | 16.2560 | 0.40% | 2.54% | 1.92% |
| 4 | W2 | 1.6122 | 0.0366 | 16.1189 | -0.07% | 1.68% | 1.09% |
| 5 | W2.1 | 1.6212 | 0.0366 | 16.2272 | 0.49% | 1.70% | 1.75% |
| 6 | W3 | 1.6250 | 0.0363 | 16.1950 | 0.72% | 0.80% | 1.55% |
| 7 | W3.1 | 1.6268 | 0.0364 | 16.2294 | 0.83% | 0.99% | 1.76% |
| 8 | W4 | 1.6608 | 0.0384 | 16.7789 | 2.86% | 6.37% | 4.98% |
| 9 | W4.1 | 1.6567 | 0.0384 | 17.2158 | 2.62% | 6.21% | 7.39% |
| 10 | W4.2 | 1.6575 | 0.0375 | 17.7137 | 2.67% | 4.14% | 9.99% |
| 11 | W5 | 1.6457 | 0.0376 | 16.1637 | 1.97% | 4.34% | 1.36% |
| 12 | W5.1 | 1.6482 | 0.0368 | 16.6184 | 2.12% | 2.07% | 4.06% |
| 13 | W5.2 | 1.6175 | 0.0360 | 16.8157 | 0.26% | 0.14% | 5.18% |
| 14 | W6 | 1.6385 | 0.0363 | 17.1893 | 1.54% | 0.82% | 7.24% |
| 15 | W6.1 | 1.6664 | 0.0363 | 17.4419 | 3.19% | 0.89% | 8.59% |
| 16 | w6.2 | 1.6753 | 0.0363 | 17.6782 | 3.70% | 0.83% | 9.81% |
| 17 | W7 | 1.6562 | 0.0372 | 17.0314 | 2.59% | 3.22% | 6.38% |
| 18 | W7.1 | 1.6553 | 0.0368 | 17.4824 | 2.54% | 2.23% | 8.80% |
| 19 | W7.2 | 1.6889 | 0.0365 | 17.8179 | 4.48% | 1.29% | 10.52% |
| 20 | W7.3 | 1.6487 | 0.0368 | 17.7184 | 2.15% | 2.26% | 10.01% |
| A/A | Config. | Range (km) | Endurance (hr) | Range Div. | Endurance Div. |
|---|---|---|---|---|---|
| 1 | Original | 110.37 | 1.34 | - | - |
| 2 | W1 | 111.81 | 1.38 | 1.29% | 3.06% |
| 3 | W1.1 | 112.53 | 1.39 | 1.92% | 3.80% |
| 4 | W2 | 111.58 | 1.37 | 1.09% | 2.52% |
| 5 | W2.1 | 112.33 | 1.38 | 1.75% | 3.30% |
| 6 | W3 | 112.11 | 1.37 | 1.55% | 2.64% |
| 7 | W3.1 | 112.35 | 1.38 | 1.76% | 2.9% |
| 8 | W4 | 116.15 | 1.46 | 4.98% | 8.64% |
| 9 | W4.1 | 119.18 | 1.52 | 7.39% | 12.24% |
| 10 | W4.2 | 122.62 | 1.58 | 9.99% | 15.33% |
| 11 | W5 | 111.89 | 1.39 | 1.36% | 3.79% |
| 12 | W5.1 | 115.04 | 1.43 | 4.06% | 6.50% |
| 13 | W5.2 | 116.41 | 1.45 | 5.18% | 7.79% |
| 14 | W6 | 118.99 | 1.49 | 7.24% | 10.02% |
| 15 | W6.1 | 120.74 | 1.52 | 8.59% | 11.97% |
| 16 | W6.2 | 122.38 | 1.55 | 9.81% | 13.63% |
| 17 | W7 | 117.90 | 1.48 | 6.38% | 9.60% |
| 18 | W7.1 | 121.02 | 1.53 | 8.80% | 12.78% |
| 19 | W7.2 | 123.34 | 1.57 | 10.52% | 14.94% |
| 20 | W7.3 | 122.65 | 1.58 | 10.01% | 15.20% |
| A/A | Config. | |||||
|---|---|---|---|---|---|---|
| 1 | Original | 0.841 | 0.0527 | 22.93 | - | - |
| 2 | W1 | 0.872 | 0.0540 | 22.51 | 3.56% | 2.30% |
| 3 | W1.1 | 0.874 | 0.0538 | 22.49 | 3.79% | 1.91% |
| 4 | W2 | 0.866 | 0.0537 | 22.59 | 2.87% | 1.81% |
| 5 | W2.1 | 0.868 | 0.0535 | 22.56 | 3.14% | 1.42% |
| 6 | W3 | 0.860 | 0.0531 | 22.67 | 2.21% | 0.67% |
| 7 | W3.1 | 0.861 | 0.0531 | 22.66 | 2.35% | 0.60% |
| 8 | W4 | 0.910 | 0.0542 | 22.04 | 7.57% | 2.73% |
| 9 | W4.1 | 0.936 | 0.0544 | 21.72 | 10.21% | 3.05% |
| 10 | W4.2 | 0.950 | 0.0536 | 21.57 | 11.51% | 1.69% |
| 11 | W5 | 0.884 | 0.0547 | 22.36 | 4.86% | 3.55% |
| 12 | W5.1 | 0.885 | 0.0533 | 22.34 | 5.03% | 1.02% |
| 13 | W5.2 | 0.889 | 0.0529 | 22.30 | 5.42% | 0.25% |
| 14 | W6 | 0.893 | 0.0520 | 22.24 | 5.89% | −1.46% |
| 15 | W6.1 | 0.907 | 0.0520 | 22.08 | 7.27% | −1.44% |
| 16 | W6.2 | 0.917 | 0.0519 | 21.96 | 8.28% | −1.69% |
| 17 | W7 | 0.902 | 0.0529 | 22.14 | 6.76% | 0.40% |
| 18 | W7.1 | 0.919 | 0.0526 | 21.92 | 8.55% | −0.28% |
| 19 | W7.2 | 0.930 | 0.0522 | 21.79 | 9.63% | −0.99% |
| 20 | W7.3 | 0.947 | 0.0534 | 21.61 | 11.19% | 1.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolaou, E.; Karatzas, E.; Kilimtzidis, S.; Kostopoulos, V. Winglet Design for Class I Mini UAV—Aerodynamic and Performance Optimization. Eng. Proc. 2025, 90, 111. https://doi.org/10.3390/engproc2025090111
Nikolaou E, Karatzas E, Kilimtzidis S, Kostopoulos V. Winglet Design for Class I Mini UAV—Aerodynamic and Performance Optimization. Engineering Proceedings. 2025; 90(1):111. https://doi.org/10.3390/engproc2025090111
Chicago/Turabian StyleNikolaou, Eleftherios, Eleftherios Karatzas, Spyridon Kilimtzidis, and Vassilis Kostopoulos. 2025. "Winglet Design for Class I Mini UAV—Aerodynamic and Performance Optimization" Engineering Proceedings 90, no. 1: 111. https://doi.org/10.3390/engproc2025090111
APA StyleNikolaou, E., Karatzas, E., Kilimtzidis, S., & Kostopoulos, V. (2025). Winglet Design for Class I Mini UAV—Aerodynamic and Performance Optimization. Engineering Proceedings, 90(1), 111. https://doi.org/10.3390/engproc2025090111








