Abstract
Naor and Shamir introduced the fundamental concept of visual cryptography (VC) in 1994. In that model, the secret image is split into two meaningless shares, allowing the secret to be revealed and recognized by the human eye just by superimposing the two shares. Since then, many scholars have studied the VC problem. To improve the efficiency of transmitting secrets, multi-secret visual cryptography has been proposed to encrypt multiple secret images at the same time. On the other hand, with the reduction in hardware costs, research on XOR-based VC has become popular to address the issue of poor image quality in the recovered image of OR-based visual cryptography, though it requires computing equipment. Scholars also have developed VC schemes utilizing OR-based decryption (equivalent to traditional VC) and XOR-based decryption. These schemes recover secrets without additional hardware (using OR-based decryption) and provide higher-quality images when extra hardware is available (using XOR-based decryption). We propose a visual multi-secret sharing scheme (VMSSS) to encrypt multiple secret images into n (>1) shares. When all shares are collected, all original secret images are decrypted by using the OR or XOR operation.
1. Introduction
Visual Cryptographic Scheme (VCS) is a method designed for securely sharing secret images. In 1994, Naor and Shamir introduced the widely recognized (t, n)-threshold VCS model, commonly referred to as (t, n) VCS [1]. This scheme encodes a binary secret image into n individual shares, each printed on a transparent sheet. The original image remains completely unrecoverable if fewer than t shares are combined. The decryption process is straightforward—when any t or more shares are overlaid using the ‘OR’ operation, the hidden image becomes visible to the human eye without requiring computational processing. Since no additional calculations or equipment are required for decryption, visual cryptography has many applications in life, such as lottery activities. Recently, many studies on merging with QR codes have been proposed.
Early implementations of VCS relied on pixel expansion, where each pixel in the secret image was mapped to multiple pixels in the generated shares. This approach inevitably led to distortion and an increase in image size upon reconstruction. This means that as more and more shares are formed, pixel expansion will make this approach practically infeasible (it could scale up a hundred or even a thousand times). To address this issue, Kafri and Keren proposed a secret-sharing technique based on the Random Grid (RG) method, which allows for black-and-white image encryption without pixel expansion [2]. Since their contribution, visual cryptography has continued to evolve, with researchers exploring new techniques to enhance efficiency and visual quality.
A visual multi-secret sharing scheme (VMSSS) differs from the previously mentioned VCS, as it simultaneously encrypts more than one secret into the same shares [3]. It reduces extra costs and enhances the efficiency of encryption. Many researchers have studied VMSSS in the past few years, focusing on limitations regarding the number and shape of secret images. At first, scholars designed a method to restore multiple images by rotating one of the shares, but this would limit the shape of the image (it must be a square) and the number of images (a maximum of four). Chang et al. [4] proposed a novel random grid-based VMSSS in 2018, which divides each secret image into several parts and then encrypts them into corresponding shares. By shifting one share by different pixels and superimposing it on the other share, the different secret image can be reconstructed separately.
In the context of visual shared secret schemes, contrast serves as the key metric for assessing the quality of the reconstructed image. It represents the distinction between the white and black regions of the secret image as observed in the restored version. Numerous definitions of contrast exist, with the most commonly used being presented in [5]. For any black and white image, the contrast value ranges from −1 to 1. In traditional VCS, the stacking operation is the OR operation, and the contrast of the reconstructed image reaches a maximum of 0.5. This low contrast limits many potential developments. To solve the above problems, XOR-based VCS was proposed [6]. The image reconstructed using the XOR operation can theoretically achieve a contrast value of 1, significantly enhancing its visual quality. However, it requires appropriate hardware equipment. Therefore, scholars have developed VC schemes using OR-based decryption and XOR-based decryption at the same time [7,8]. These schemes can recover secrets without additional hardware (using OR-based decryption) and provide higher-quality recovered images when light hardware is available (using XOR-based decryption).
VMSSS was previously designed as a method to encrypt multiple secret images into two shares, i.e., (2, 2) VCS, e.g., [4]. However, there is still a need for an (n, n) VCS that can encrypt multiple secret images simultaneously and recover the secret image by using OR or XOR operations without pixel expansion. This is useful in situations where more than two parties want to share multiple secrets. This allows for the recovery of secrets without extra hardware via OR-based decryption and offers higher-quality recovered images when additional hardware is used through XOR-based decryption. Huang et al. proposed an (n, n) XOR-based visual multi-secrets sharing scheme [9]. This method addressed the limitation in Chang et al.’s approach [4], which only encrypts the secret images into two shares, i.e., (2, 2) VMSSS, allowing for more than two participants. Although Huang et al.’s scheme secures the capability of XOR decryption, the OR operation can also be used in the decryption phase simultaneously, although the result is relatively poor. However, when n > 3, even the reconstruction result of the XOR operation is not satisfactory [9]. Therefore, we designed an improved method to solve this problem.
2. Preliminaries
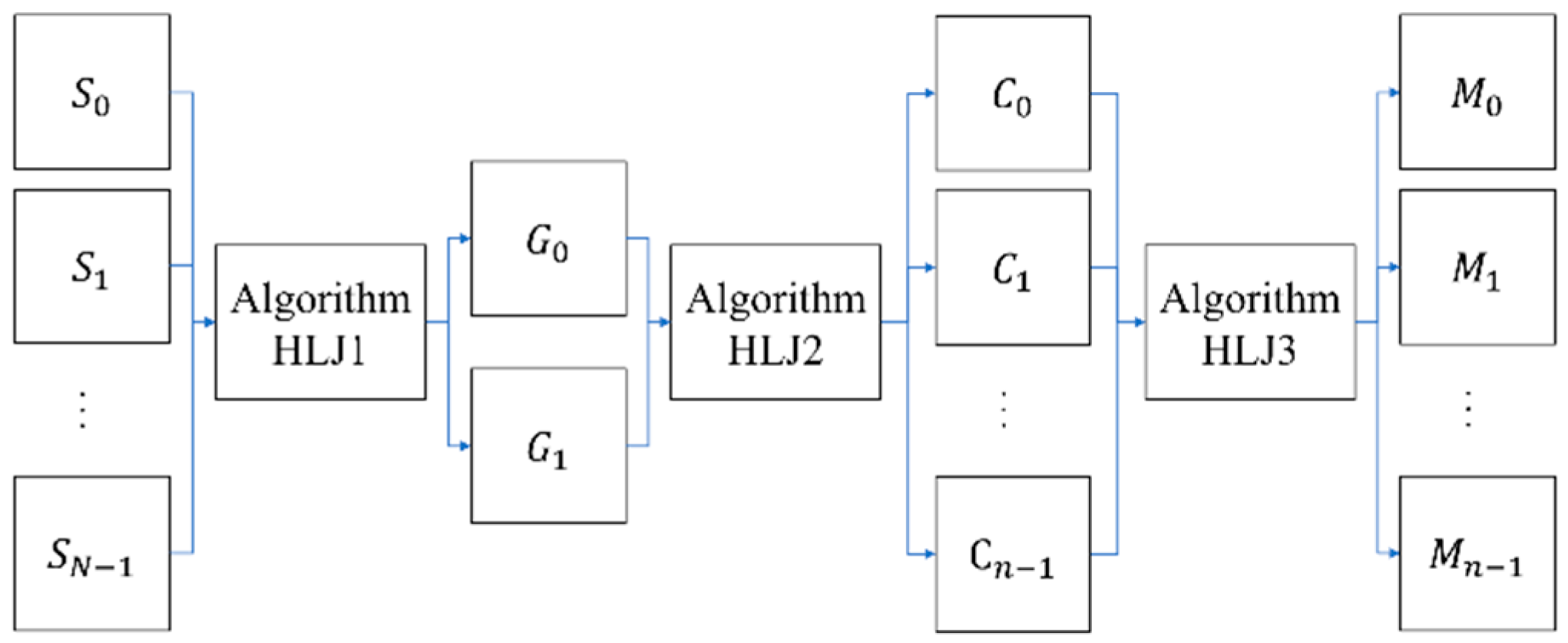
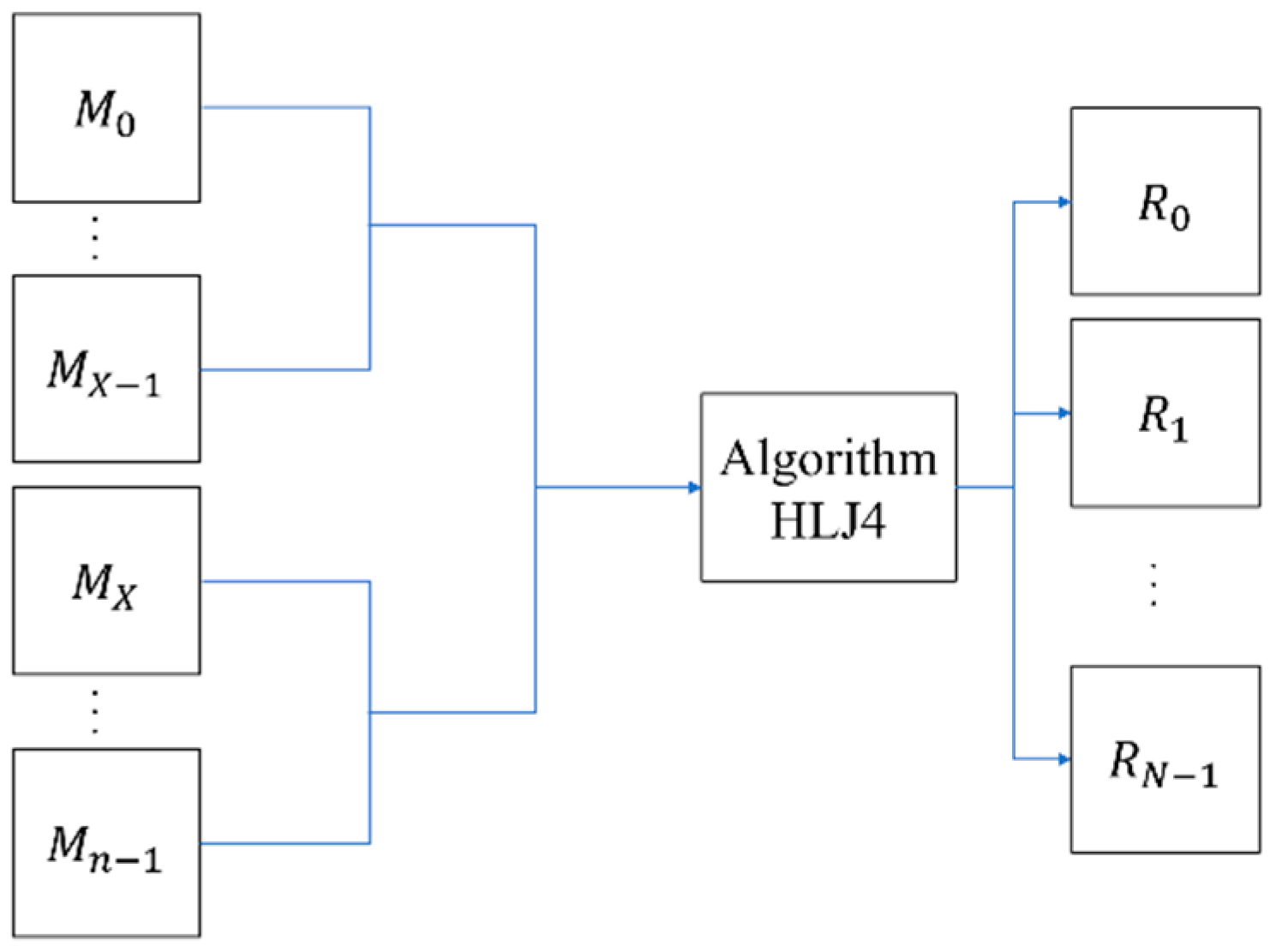
Huang et al. proposed an (n, n) XOR-based visual multi-secret scheme with meaningful shares [9]. Their approach incorporates three algorithms within the encryption process, whereas the decryption process consists of only a single algorithm. The encryption and decryption process are illustrated in Figure 1 and Figure 2, respectively.
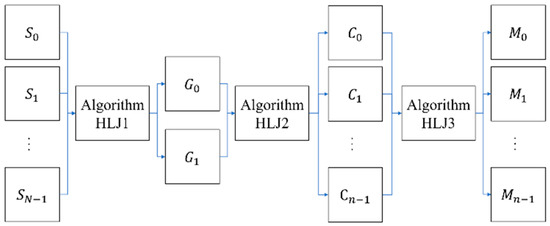
Figure 1.
The encryption process model of Huang et al.’s scheme [9].
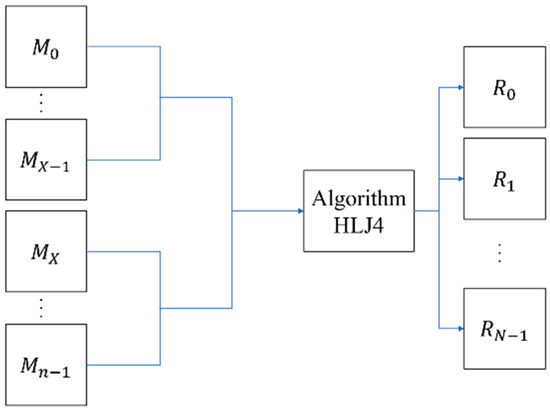
Figure 2.
The decryption process model of Huang et al.’s scheme [9].
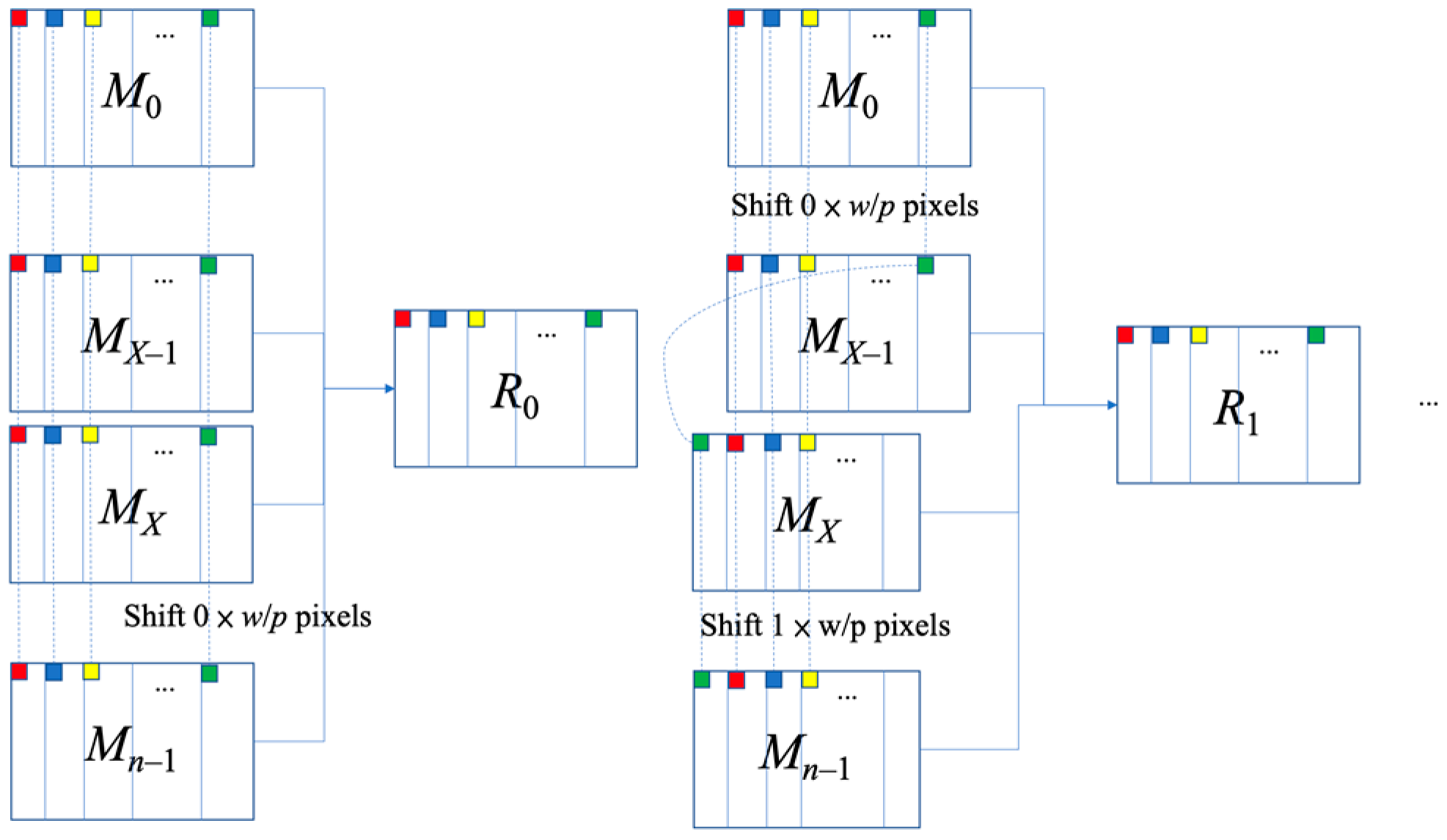
Reference [9] used Algorithm HLJ1 to enable all secret images to be restored using two shares, then expands these two shares into n shares (Algorithm HLJ2), and finally adds the camouflage algorithm (Algorithm HLJ3). When restoring with this scheme, n shares are stacked by using the XOR operation to restore—after shifting the last N−X shares by (i−1)w/p pixels (Figure 3). All the shares are superimposed to perform the XOR operation and obtain the restored image i. Where N represents the number of secret images, X = ⌈n/2⌉, w is the width of the image, and p is a parameter that can be selected by the user.
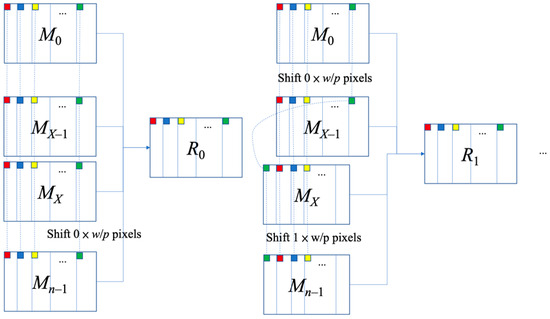
Figure 3.
The illustrative diagram of Algorithm HLJ4 [9] (areas with small squares of the same color will be stacked in the same position).
Huang et al.’s scheme uses the parameter to control the proportion of camouflage in the shares. A higher value makes the shares more similar to the camouflage images. However, when other parameters remain constant, the restoration quality decreases as increases. If no camouflage is used (γ = 0), the restoration quality of the restored image becomes the highest. In addition, this scheme also can restore the secret image by using the OR operations, but the restoration quality becomes poor. Figure 4 presents the experimental results of Huang et al.’s scheme when γ = 0 with . Even though Huang et al.’s scheme performs well, its distortion increases, especially when N is larger. This is because it first uses the Chang et al.’s scheme [4] to encrypt all secret images into two shares, and then expand them into n shares. This process will cause great distortion, because only two shares can obtain information related to the original secrets, resulting in the fact that most of the pixels of those secret images cannot be accessed. That is, they are not encrypted into the share. Therefore, this paper develops a new scheme with similar goals to the scheme of Huang et al., but because it uses a direct encryption of all secret images into n shares, it can access most of the pixels of those secret images, which will greatly reduce the distortion and achieve better results.

Figure 4.
Experimental results by Huang et al.’s scheme with (a–d) Secret images S0, …, and S3; (e–h) shares M0, …, and M3; (i–l) OR-restored images R0, R1, R2, and R3; and (m–p) XOR-restored images XR0, XR1, XR2 and XR3.
3. Main Results
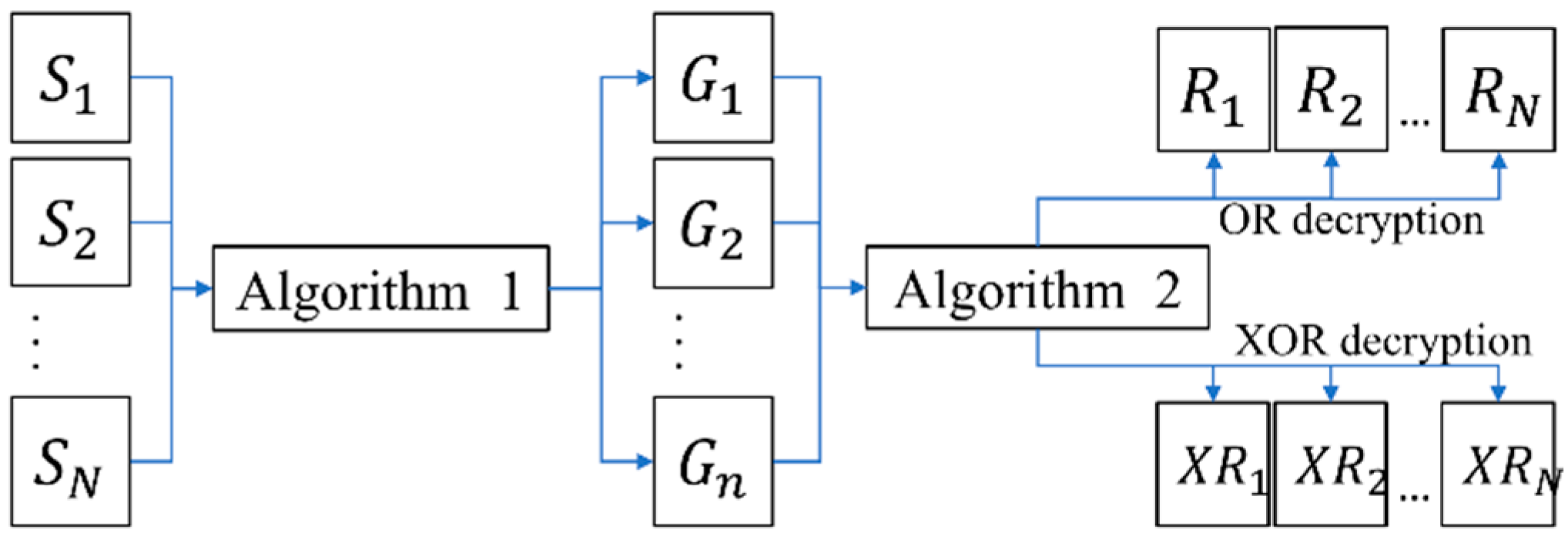
The proposed VMSSS simultaneously encrypts N secret images and distributes n shares to n participants. After collecting the shares of all participants, these N secret images are decrypted using OR or XOR operations simultaneously. Figure 5 illustrates the model of the proposed encryption and decryption process. From the figure, we can clearly see that the proposed scheme directly uses Algorithm 1 to complete the encryption stage, which is relatively simple compared to the method in [9]. The decryption process is just to shift all the collected shares according to the rules separately and then stack them up.
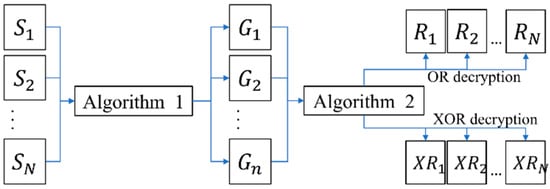
Figure 5.
The model of the proposed scheme.
To simplify the expression, some notations and parameters are listed in Table 1. For the ease of comparison, we mostly use the same symbols and definitions as in [9]. This is also adopted by most of the literature.

Table 1.
Some notations and parameters used in this work.
3.1. Encryption Algorithm
Due to space limitations, this paper only discusses the case where N = n. Algorithm 1 encrypts N secret images (of the same size) on N = n shares. In this way, any N participants can individually obtain their shares. During recovery, if any of them do not hand over the shares they have kept, then any secret image is not recovered. The main idea of Algorithm 1 is to learn from [4] and first design a method to move n shares when restoring the secret images. Then, for a group of pixels, a secret is randomly selected to be encrypted in order. That is, once a secret image and location are selected, the secret image and a whole set of pixels corresponding to the location will be encrypted into the shares at once.
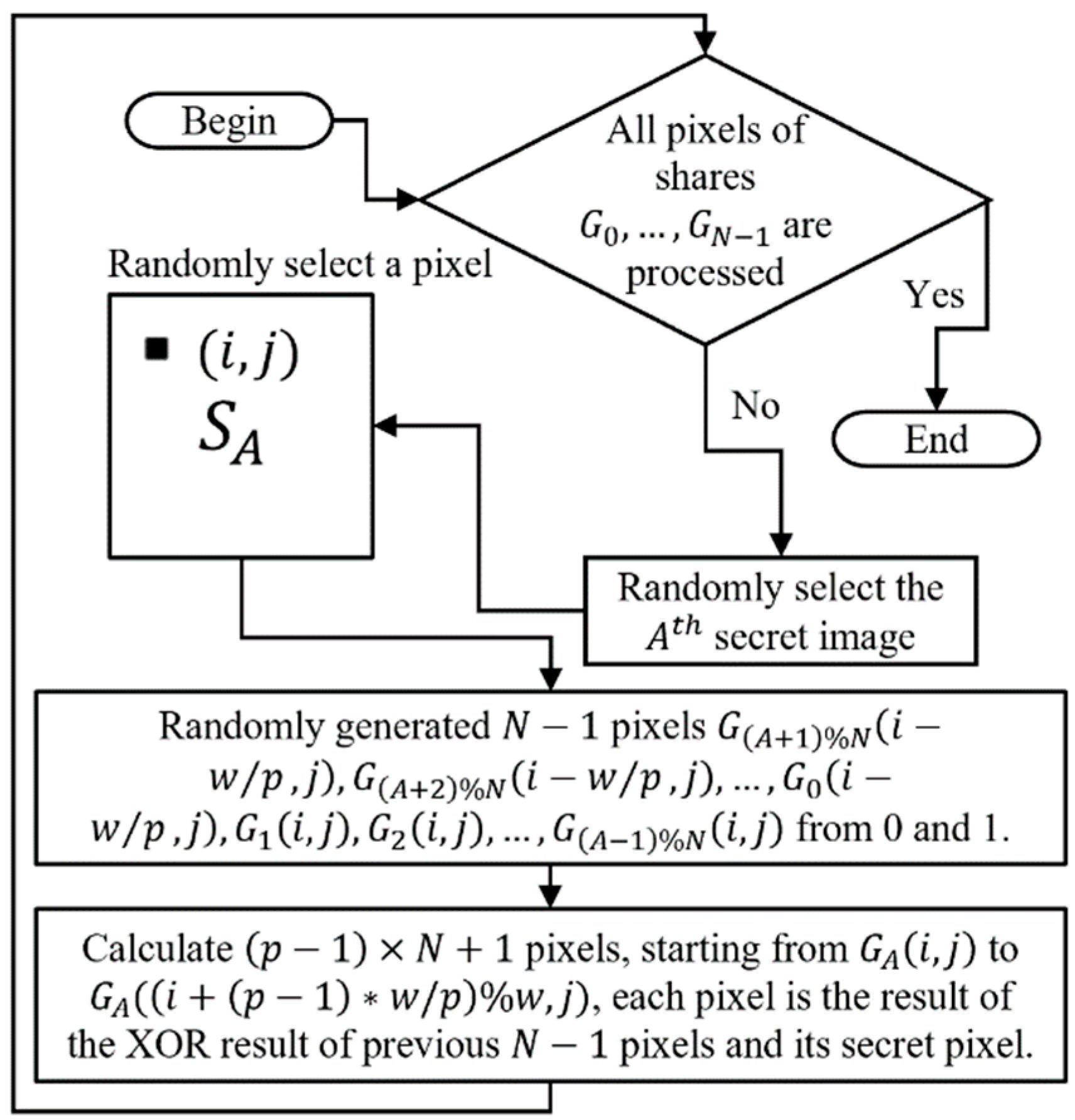
To provide a clear understanding of Algorithm 1, the flowchart is shown in Figure 6. In Algorithm 1, Step 4 calculates the pixel selected at the beginning, which is the (i, j) position of the A-th share, and its result is the XOR result of the corresponding secret image pixel and all randomly generated pixels in Step 3. We divide each share into p equal parts, with the k-th part of the second share () to the k-th part of the N-th share () and the (k + 1)-th part of the first share () to form a group. Before processing the entire group, we complete the calculations for the redundant parts in Step 5 to fully process groups in Step 6, which amounts to pixels. In Step 7, we calculate the remaining pixels (ranging from A to N, depending on the chosen A). The required calculations are finished once A, i, and j are selected. In other words, selecting A, i, and j generates randomly produced pixels and calculated pixels.
| Algorithm 1. (N, N) Visual N Secret Sharing Scheme |
Input: N secret images of size pixels, and a divisor of : p (which must coprime to ). Output: shares of size .
|
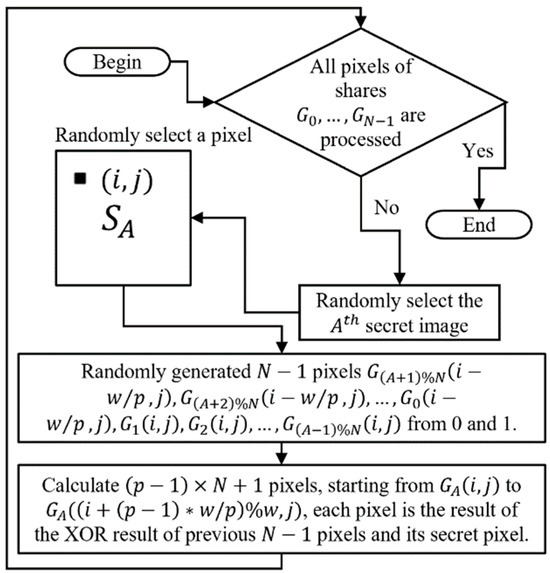
Figure 6.
A flow chart of Algorithm 1.
3.2. Decryption Algorithm
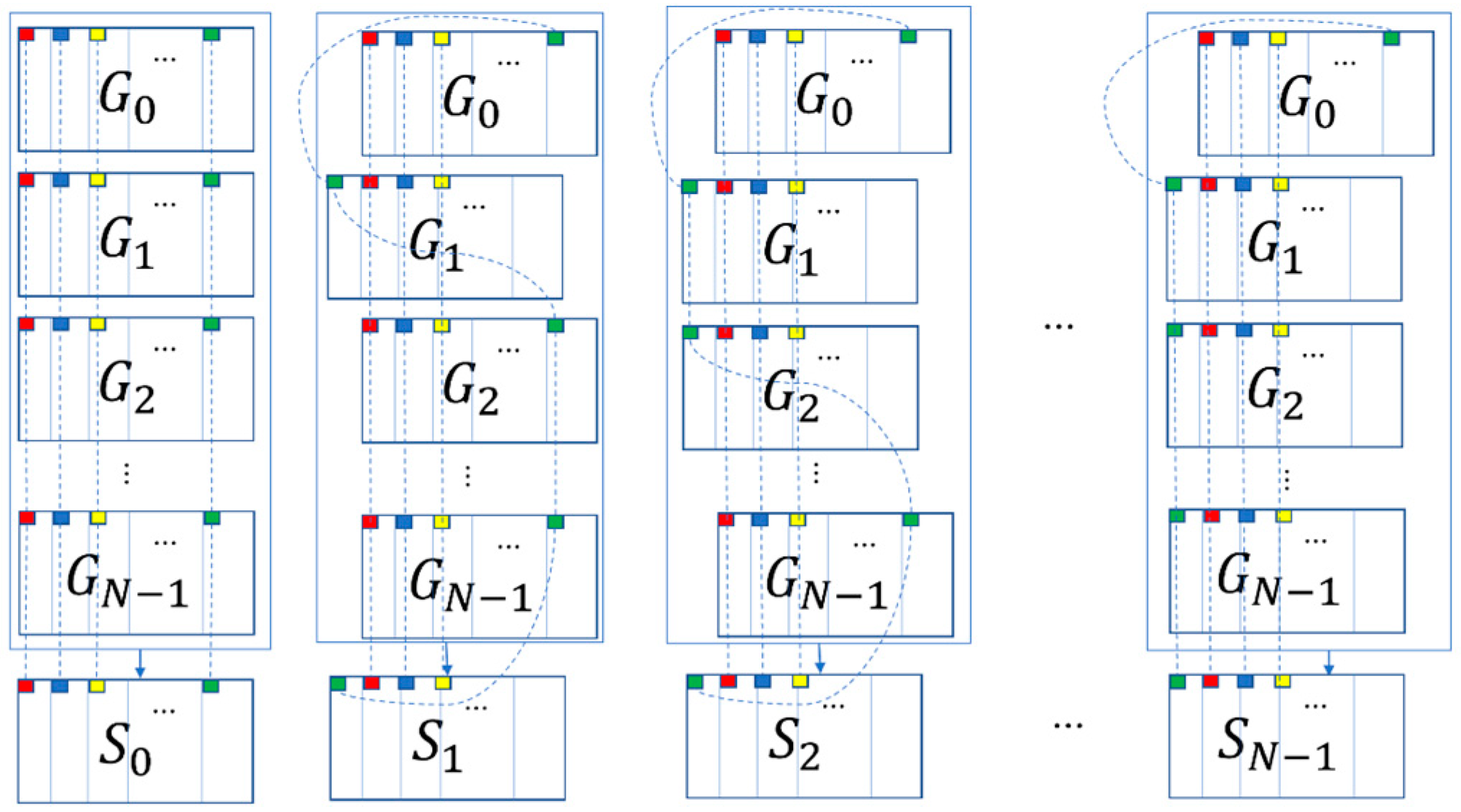
Algorithm 2 decrypts to reconstruct the image. To restore any secret image, all shares must be collected and all secret images can be restored at the same time. In Algorithm 2, to reconstruct the initial secret image (), all the shares are directly overlaid. To restore the second secret image (), the second share () must be shifted cyclically pixels to the left. This means that the leftmost pixels of the second share must be moved and connected to the rightmost and stacked together with the other shares. Similarly, to reconstruct the third secret image (), both the second and third shares () need to be shifted cyclically pixels to the left. In general, to restore the t-th secret image, the second to the t-th shares must be shifted cyclically pixels to the left (). The pixels moved to the left are added to the rightmost part of the share, where is the width of the secret image (=the width of any share), and p is a parameter that is a divisor of the chosen by the user. The schematic illustrating this process is shown in Figure 7.
| Algorithm 2. Decryption Algorithm |
Input: shares of size , a divisor of : p. Output: reconstructed images by OR operation and reconstructed images by XOR operation of size .
|
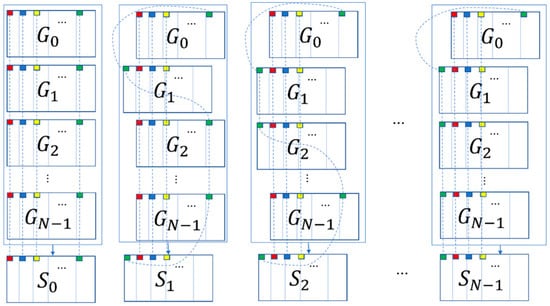
Figure 7.
The schematic diagram of Algorithm 2 (areas with small squares of the same color will be stacked in the same position).
3.3. Experimental Results
This subsection provides two experiments for a subsequent comparison with the method proposed in [9]. In the initial experiment, we encrypted three secret images, whereas in the subsequent experiment, four secret images were encrypted. All images measure 500 × 500 pixels in size, with the parameter p consistently set to 20 across both experiments. The three secret images utilized in the initial experiment are depicted in Figure 8a–c, whereas the quartet of secret images employed in the subsequent experiment correspond to those illustrated in Figure 4a–d. Figure 9 shows the first experiment result by the proposed (n, n) VMSSS. Where the OR-reconstructed image refers to the image reconstructed through the OR operation, the XOR-reconstructed image refers to the image reconstructed through the XOR operation.
Figure 8.
(a–c) Secret images S0, S1, and S2 for the first experiment.

Figure 9.
The first experiment results from the proposed (3, 3) VMSSS. (a–c) Shares G0, G1, and G2; (d–f) OR-reconstructed images R0, R1, and R2; and (g–i) XOR-reconstructed images XR0, XR1, and XR2.
Figure 10 displays the results of the second experiment using the proposed (n, n) VMSSS. Since we used the same secret images for encryption, the experimental results can be directly compared with the results of [9] (Figure 4). The results demonstrate that the proposed scheme encrypts N secret images into N meaningless shares, ensuring that no visual information can be discerned from any individual share. However, when OR or XOR operations are applied, the original secret images can be clearly restored with high visibility. This confirms that the proposed method is an (n, n)-threshold visual multi-secret sharing scheme capable of concealing information completely during encryption while enabling a clear reconstruction during decryption.

Figure 10.
The second experiment results by the proposed (4, 4) VMSSS. (a–d) Shares G0, G1, G2, and G3; (e–h) OR-reconstructed images R0, R1, R2, and R3; and (i–l) XOR-reconstructed images XR0, XR1, XR2, and XR3.
3.4. Analysis
The effectiveness of a visual secret sharing scheme is often assessed by analyzing the quality of the reconstructed image. A key metric is often used to define the quality of reconstructed images. Contrast, often labeled , with higher contrast values indicates a reconstructed image of a better quality [4]. The contrast value ranges between −1 and 1, with a contrast value of 1 indicating a perfect reconstruction, and 0 signifying that the reconstructed image is meaningless in relation to the original image.
Similar to [9], to articulate the concept of contrast, the average light transmittance T(R) is employed, representing the ratio of white pixels to the total pixel count in image R. The notations (and (, respectively) refers to the average transmittance of the area of image R that corresponds to the white (transparent) regions (and black (opaque) regions, respectively) of image S. This concept applies to both the secret image S and the reconstructed image R. Once the definition is understood, the average light transmittance for the proposed scheme is subsequently computed.
The average light transmittance formulas of this scheme based on the OR and XOR decryptions are (1) to (4). After calculating the average light transmittance, the theoretical average contrast value is determined according to the contrast equation as in (5) and (6).
Since both and are greater than 0 (p is a positive integer), the correctness of the proposed scheme is also verified. In the following, we present a numerical analysis of the results from experiments one and two. The theoretical values and experimental data are listed in Table 2. The experimental data represent the average values from all reconstructed images. Compared with the previous result [9], the reconstructed image both by the OR and XOR operations of the proposed scheme has a higher contrast overall. The highest contrast of the restored image by the OR operation is (4p—2)/(2NNp + (N—2)p + 1), and that by the XOR operation of is (4p—2)/(3Np—2p + 1) in [9]. When the above two formulas are compared with (5) and (6), the proposed scheme demonstrates a better performance than the one in Ref. [9] in both decryption methods. At the same N and p values, the proposed scheme performs satisfactorily, and the restored image using the XOR operation is almost completely restored as displayed in Table 2 (the value close to 1).

Table 2.
The theoretical and average experimental contrasts of the restored images generated by experiment 1 and 2.
4. Conclusions
In this paper, a novel (n, n) visual multi-secret sharing scheme with OR and XOR decryption capabilities is developed. The proposed scheme is to directly encrypt N secret images into n shares, so the recovered images are of a high quality. Especially when using XOR decryption, it is almost completely restored. In addition, the parameter p in the proposed VMSSS is determined by the user, enhancing the flexibility of the proposed scheme. Users can adjust the parameters according to their specific needs. The introduced VMSSS is both secure and efficient, boasting several key characteristics:
- An absence of pixel expansion;
- High visual quality in the reconstructed images;
- A flexible adjustability of the parameter ;
- The capability to encrypt multiple secrets at the same time;
- The secret image can be restored by employing either an OR operation or an XOR operation.
The comparison of the proposed VMSSS against prior research findings is shown in Table 3. Among them, [1,2,8] are schemes that can only encrypt a single secret image, while [4] supports decryption solely through the OR operation. Only [9] offers the same functionality as our proposed scheme; however, as discussed in the previous section, our reconstruction results are superior. Although this paper only shows the results when the quantity of secret images N is equal to the quantity of shares n (), the other two (n, n) VMSSSs have also been designed when (for and ). This means that there can be no limit between the quantity of images and the quantity of participants, and the proposed (n, n) VMSSS can decrypt high-quality recovered images using the OR or XOR operations. The proposed scheme has many development possibilities, including the transformation of nonsensical shares into meaningful ones, and using grayscale and color images for the encryption process. In addition, designing an MVSSS that can achieve a higher quality when using OR operation restoration is also an interesting topic that can be studied in the future.

Table 3.
A comparative analysis of the proposed VMSSS against related works.
Author Contributions
Conceptualization, J.S.-T.J. and A.-H.L.; methodology, J.S.-T.J. and A.-H.L.; software, A.-H.L.; validation, J.S.-T.J.; formal analysis, J.S.-T.J. and A.-H.L.; investigation, A.-H.L.; data curation, A.-H.L.; writing—original draft preparation, A.-H.L.; writing—review and editing, J.S.-T.J.; visualization, A.-H.L.; supervision, J.S.-T.J.; project administration, J.S.-T.J.; funding acquisition, J.S.-T.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Science and Technology Council, R.O.C. under grant NSTC 112-2115-M-260-001-MY2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Naor, M.; Shamir, A. Visual Cryptography. In Advances in Cryptology—EUROCRYPT′94: Workshop on the Theory and Application of Cryptographic Techniques Perugia, Italy, 9–12 May 1994; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kafri, O.; Keren, E. Encryption of pictures and shapes by random grids. Opt. Lett. 1987, 12, 377–379. [Google Scholar] [PubMed]
- Lin, K.S.; Lin, C.H.; Chen, T.H. Distortionless visual multi-secret sharing based on random grid. Inf. Sci. 2014, 288, 330–346. [Google Scholar] [CrossRef]
- Chang, J.J.-Y.; Huang, B.-Y.; Juan, J.S.-T. A New Visual Multi-Secrets Sharing Scheme by Random Grids. Cryptography 2018, 2, 24. [Google Scholar] [CrossRef]
- Eisen, P.A.; Stinson, D.R. Threshold visual cryptography schemes with specified whiteness levels of reconstructed pixels. Des. Codes Cryptogr. 2002, 25, 15–61. [Google Scholar] [CrossRef]
- Tuyls, P.; Hollmann, H.D.; Lint, J.V.; Tolhuizen, L.M.G.M. XOR-based visual cryptography schemes. Des. Codes Cryptogr. 2005, 37, 169–186. [Google Scholar]
- Wu, X.; Sun, W. Random grid-based visual secret sharing with abilities of OR and XOR decryptions. J. Vis. Commun. Image Represent. 2013, 24, 48–62. [Google Scholar]
- Lin, Y.-R.; Juan, J.S.-T. RG-Based (k, n)-Threshold Visual Cryptography with Abilities of OR and XOR Decryption. Eng. Proc. 2023, 55, 65. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Lo, A.-H.; Juan, J.S.-T. (n, n) XOR-based Visual Multi-secrets Sharing Scheme with Meaningful Shares. In Proceedings of the 2022 IEEE 5th International Conference on Knowledge Innovation and Invention (ICKII), Hualien, Taiwan; 2022; pp. 69–74. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).