Reinforcement Learning for UAV Path Planning Under Complicated Constraints with GNSS Quality Awareness †
Abstract
1. Introduction
2. Methodology
2.1. Rewards/Penalties Formulation
- Distance Reward
- Arrival Reward
- Dilution of Precision
- No-Fly Zone
- Obstacle Avoidance
- Altitude Restriction
- Timeout Penalty
- Out-of-Bounds Restriction
2.2. Observation Methods
- Raycast3D sensor
- Reading data from the environment’s physics engine.
- DoP predictor
3. Experiments and Results
3.1. DoP Representation and Grading
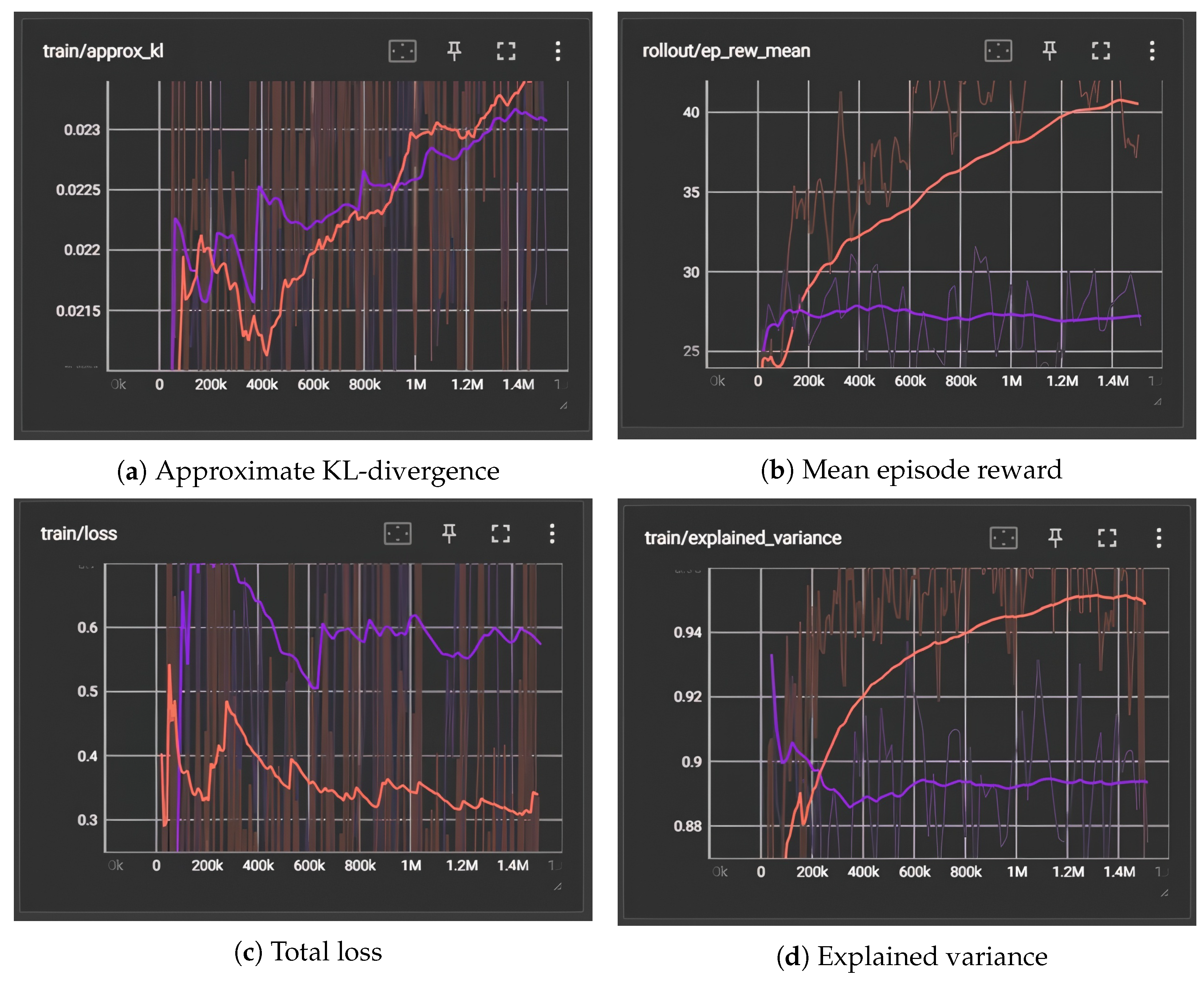
3.2. Training Performance Analysis
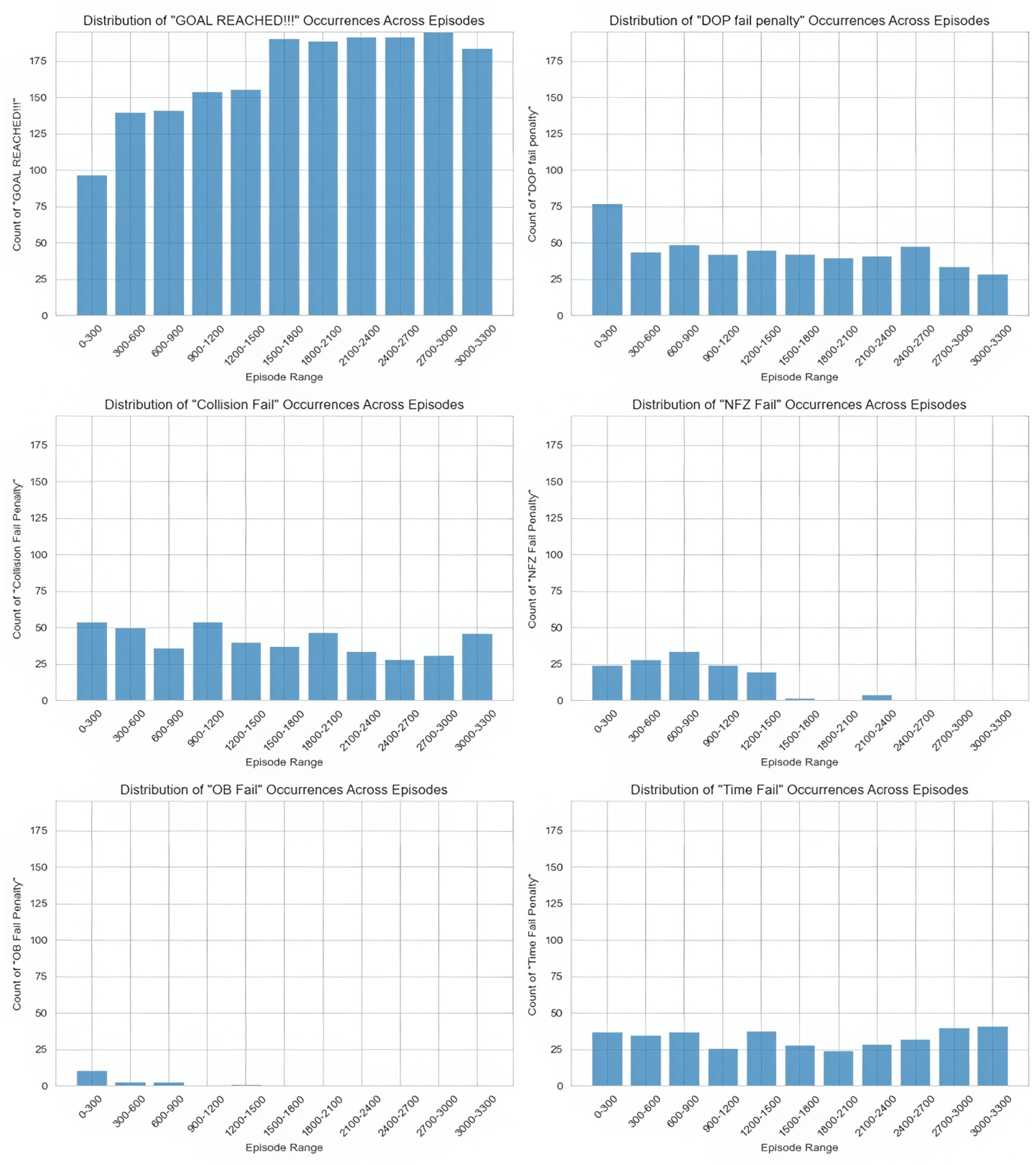
3.3. Success Rate Analysis
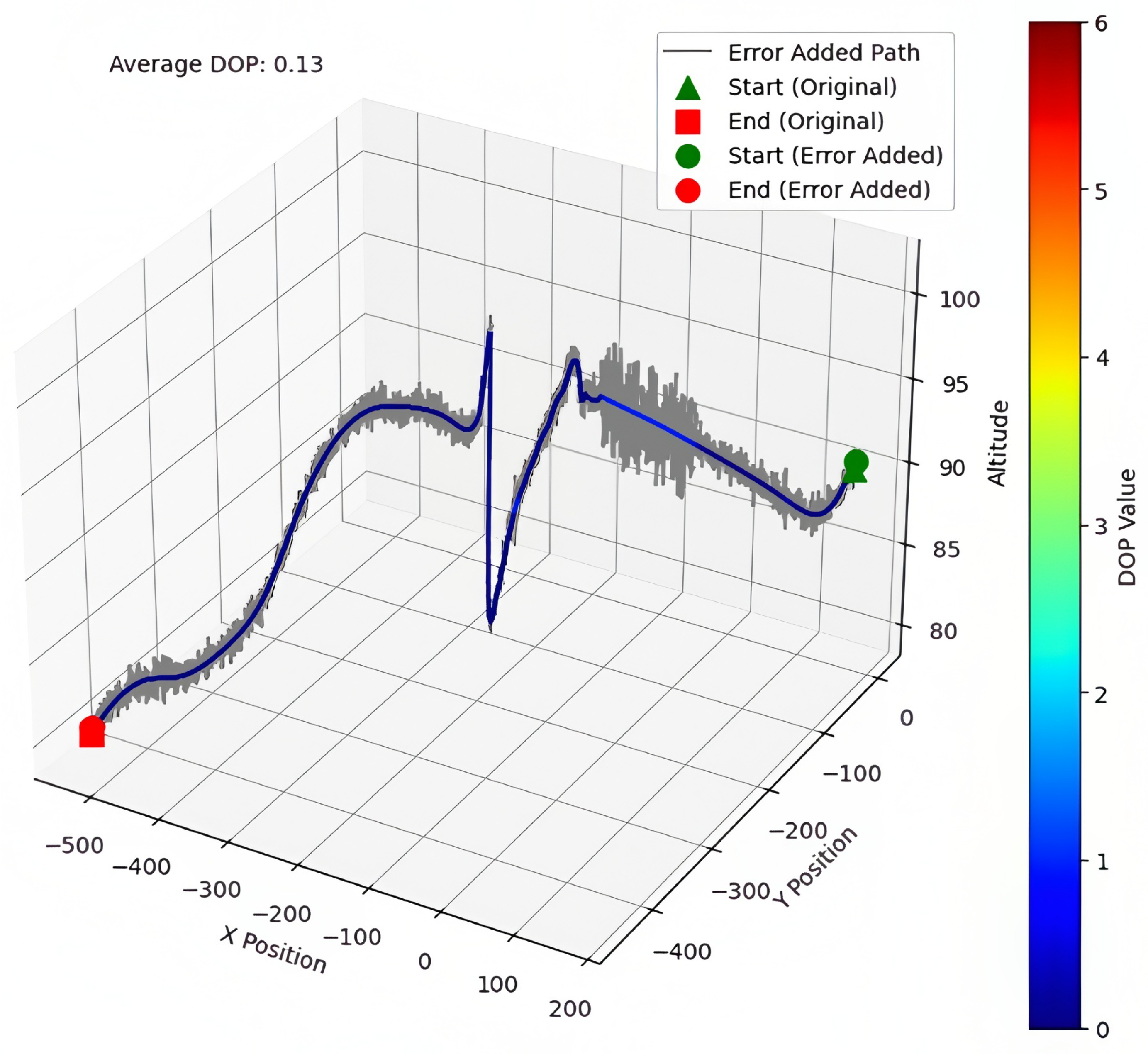
3.4. Position Error Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tabassum, T.E.; Xu, Z.; Petrunin, I.; Rana, Z.A. Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments. Aerospace 2023, 10, 923. [Google Scholar] [CrossRef]
- Yang, Y.; Khalife, J.; Morales, J.J.; Kassas, Z.M. UAV waypoint opportunistic navigation in GNSS-denied environments. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 663–678. [Google Scholar] [CrossRef]
- Karimi, H.A.; Asavasuthirakul, D. A novel optimal routing for navigation systems/services based on global navigation satellite system quality of service. J. Intell. Transp. Syst. 2014, 18, 286–298. [Google Scholar] [CrossRef]
- Ragothaman, S.; Maaref, M.; Kassas, Z.M. Autonomous ground vehicle path planning in urban environments using GNSS and cellular signals reliability maps: Simulation and experimental results. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2575–2586. [Google Scholar] [CrossRef]
- Zhang, G.; Hsu, L.T. A new path planning algorithm using a GNSS localization error map for UAVs in an urban area. J. Intell. Robot. Syst. 2019, 94, 219–235. [Google Scholar] [CrossRef]
- Shetty, A.; Gao, G.X. Predicting state uncertainty for GNSS-based UAV path planning using stochastic reachability. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 131–139. [Google Scholar]
- Ru, J.; Yu, H.; Liu, H.; Liu, J.; Zhang, X.; Xu, H. A Bounded Near-Bottom Cruise Trajectory Planning Algorithm for Underwater Vehicles. J. Mar. Sci. Eng. 2022, 11, 7. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Xue, L.; Li, X.; Guo, W.; Yu, S.; Ru, J.; Xu, H. Multi-objective Collaborative Optimization Algorithm for Heterogeneous Cooperative Tasks Based on Conflict Resolution. In Proceedings of the International Conference on Autonomous Unmanned Systems; Springer: Singapore, 2021; pp. 2548–2557. [Google Scholar]
- Zhu, A.; Li, J.; Lu, C. Pseudo View Representation Learning for Monocular RGB-D Human Pose and Shape Estimation. IEEE Signal Process. Lett. 2022, 29, 712–716. [Google Scholar] [CrossRef]
- Zhu, A.; Li, K.; Wu, T.; Zhao, P.; Hong, B. Cross-Task Multi-Branch Vision Transformer for Facial Expression and Mask Wearing Classification. J. Comput. Technol. Appl. Math. 2024, 1, 46–53. [Google Scholar]
- Anyaegbu, E.; Hansen, P. GNSS Performance Evaluation for Deep Urban Environments using GNSS Foresight. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 1127–1136. [Google Scholar]
- Anyaegbu, E.; Hansen, P.; Peng, B. Performance Improvement Provided by Global Navigation Satellite System Foresight Geospatial Augmentation in Deep Urban Environments. Eng. Proc. 2023, 54, 58. [Google Scholar]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable Reinforcement Learning Implementations. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Harriman, D.A.; Wilde, J.; Ober, P. EUROCONTROL’s predictive RAIM tool for en-route aircraft navigation. In Proceedings of the 1999 IEEE Aerospace Conference. Proceedings (Cat. No. 99TH8403), Snowmass, CO, USA, 7 March 1999; Volume 2, pp. 385–393. [Google Scholar]

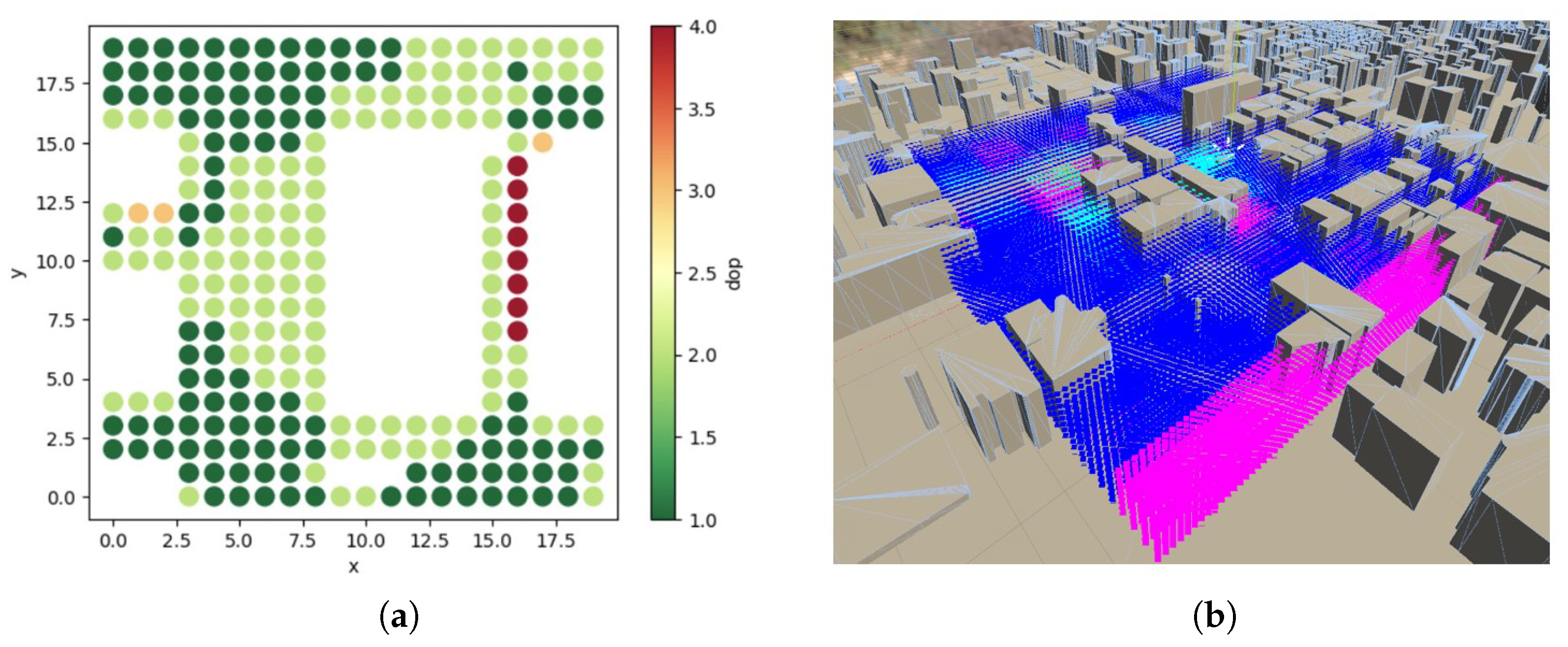
| PDoP Value Range | DoP Representation | DoP Numerical Representation | Position Error/m |
|---|---|---|---|
| 0–1 | Ideal | 0 | 0.5 |
| 1–2 | Excellent | 1 | 1.5 |
| 2–5 | Good | 2 | 3.5 |
| 5–10 | Moderate | 3 | 7.5 |
| 10–20 | Fair | 4 | 15 |
| 20+ | Poor | 5 | 30 |
| No DoP | No DoP | 6 | 30 |
| Conf. 1 | Arrival Reward | Dist. Reward | DoP Penalty | Obstacle Penalty | Altitude Penalty | NFZ Penalty |
| 20 | 0.05 | −10 | −10 | −10 | −10 | |
| Bounds Penalty | Timestep Penalty | Per Frame Penalty | Dop Penalty | DoP Tensor Size | Entropy Coefficient | |
| −5 | −5 | −0.01 | −0.01 | 27 (3 m × 3 m × 3 m) | 0.0005 | |
| Conf. 2 | Arrival Reward | Dist. Reward | DoP Penalty | Obstacle Penalty | Altitude Penalty | NFZ Penalty |
| 20 | 0.05 | −7 | −10 | −8 | −8 | |
| Bounds Penalty | Timestep Penalty | Per Frame Penalty | Dop Penalty | DoP Tensor Size | Entropy Coefficient | |
| −5 | −5 | −0.05 | −0.07 | 125 (5 m × 5 m × 5 m) | 0.001 |
| Condition | DoP Tensor Volume | DoP Fail | Collision Fail | Arrival Rate |
|---|---|---|---|---|
| Model 1 | 5 m × 5 m × 5 m | 12% | 0% | 63% |
| Model 2 | 3 m × 3 m × 3 m | 32% | 0% | 27% |
| Condition | Alt Limit | Out of Bounds | Timeout | NFZ Penalty |
| Model 1 | 0% | 0% | 25% | 0% |
| Model 2 | 0% | 0% | 41% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyammahi, A.; Xu, Z.; Petrunin, I.; Peng, B.; Grech, R. Reinforcement Learning for UAV Path Planning Under Complicated Constraints with GNSS Quality Awareness. Eng. Proc. 2025, 88, 66. https://doi.org/10.3390/engproc2025088066
Alyammahi A, Xu Z, Petrunin I, Peng B, Grech R. Reinforcement Learning for UAV Path Planning Under Complicated Constraints with GNSS Quality Awareness. Engineering Proceedings. 2025; 88(1):66. https://doi.org/10.3390/engproc2025088066
Chicago/Turabian StyleAlyammahi, Abdulla, Zhengjia Xu, Ivan Petrunin, Bo Peng, and Raphael Grech. 2025. "Reinforcement Learning for UAV Path Planning Under Complicated Constraints with GNSS Quality Awareness" Engineering Proceedings 88, no. 1: 66. https://doi.org/10.3390/engproc2025088066
APA StyleAlyammahi, A., Xu, Z., Petrunin, I., Peng, B., & Grech, R. (2025). Reinforcement Learning for UAV Path Planning Under Complicated Constraints with GNSS Quality Awareness. Engineering Proceedings, 88(1), 66. https://doi.org/10.3390/engproc2025088066






