Abstract
Industrial progress has increased the need to improve the productivity of production systems. In this context, optimizing the problem of allocating and balancing workers on a multi-manned assembly line (MALW-a-BP) is a major challenge. This paper introduces a mathematical model for this issue, as well as a hybrid genetic algorithm (h-GA) dedicated to its solution, with a particular focus on multi-objective optimization, which includes minimizing the cycle time and the total squared workload. Experimental results show that the proposed method outperforms the classical version of the GA, thus confirming the robustness and efficiency of the h-GA.
1. Introduction
Industry evolution and changing customer demands have put pressure on productivity improvements. As a result, optimizing the Multi-manned Assembly Line Worker allocation and Balancing Problem (MALW-a-BP) is a complex manufacturing challenge [1]. In this situation, multiple workers are able to collaborate on the product at a single workstation, removing the simple ALBP constraint of one worker per workstation [2].
The work of Zheng et al. [3] established a mathematical model (MM) for balancing problems on two-sided ALs, incorporating additional constraints that take into account worker skills and line efficiency. This model aims to maximize line efficiency while minimizing costs associated with workers and the smoothing index as a multi-objective (MO) problem. This study demonstrates the importance of an integrated heuristic method for solving the problem. Furthermore, a study by Moreira et al. [4] addressed the integration of workers in the production process, and proposed regularity and cycle time criteria as metrics to assess worker integration and productivity. This approach highlights the need to optimize not only task allocation but also the interaction between workers to maintain high levels of productivity. In addition, the researchers present a MM and develop heuristics to address this issue. Furthermore, the study by Yilmaz and Yilmaz [5] on the MALW-a-BP, considering assignment constraints, highlights the importance of minimizing the number of workers for a given . In addition, the tabu search method is developed as a metaheuristic to solve the test problems.
In addition, the literature has recently seen notable methodological advancements. For instance, Hashemi-Petroodi et al. [6] proposed an advanced method for task assignment in mixed-model MALs (MiM-MALs), focusing on the complexity and variability inherent in modern production environments. To address large instances, they used two heuristic approaches. In a recent work of the same authors [7], an innovative approach based on Markov decision processes was developed to model the interactions between tasks and workers dynamically. This approach addresses the task assignment problem in MALs, which include MiM and walking workers.
Numerous reviews and studies in the literature recommend using hybrid approaches to address MO-ALBPs [8,9,10,11]. Consequently, this paper introduces a new MM for the MO-MALW-a-BP and proposes a hybrid genetic algorithm (h-GA) dedicated to its solution. The goals of the MM are the minimization of and workload imbalance. The rest of this article is divided into three sections. Section 2 presents the formulation of the MO-MALW-a-BP. Section 3 contains the proposed h-GA and the computational results of the problem. Section 4 summarizes the conclusions.
2. Mathematical Model of MO-MALW-a-BP
In this study, the authors propose a multi-objective mathematical model for the MALW-a-BP in a hybrid parallel–serial AL to manufacture a single product. The goal is to optimize two objectives simultaneously: cycle time minimization and workload imbalance minimization. Azizoğlu and İmat [12] demonstrated that, in order to obtain a smoothed workload, it is equivalent to minimizing the sum of workloads squared. The notations employed in this work to analyze the problem are listed below.
2.1. Notation
| Task index, where is the number of tasks. | |
| Workstation index, where is the number of workstations. | |
| Worker index, where is the number of regular workers, is the auxiliary worker, and is the number of stations. | |
| Regular worker index. | |
| Time of task when performed by the worker. | |
| Time of task when performed by the auxiliary worker. | |
| Lower bound of . | |
| Set of predecessors of the task. | |
| Sum of workloads squared. | |
| Idle time. | |
| Start time of the task allocated to worker at workstation . | |
| End time of the task allocated to worker at workstation s. | |
| Set of tasks assigned to a regular worker during the performance of task by the auxiliary worker at workstation , taking into account the fact that both workers are working simultaneously at the same workstation. | |
| Set of tasks assigned to the worker. | |
2.2. Mathematical Model
The aim of this study is to reduce (1) and (2) simultaneously. Constraint (3) guarantees that each task is allocated to a single worker at a single workstation . Constraint (4) ensures that only one regular worker can be assigned to workstation . Constraint (5) ensures that the auxiliary worker is assigned to exactly one workstation. Constraint (6) represents the cycle time constraint. Constraint (7) guarantees the priority relations between the set of tasks . Constraint (8) guarantees that the auxiliary worker can only be allocated to workstation if a regular worker is also assigned to that workstation. Constraint (9) ensures that, in a multi-manned workstation, the total processing time of tasks allocated to the auxiliary worker is less than or equal to the total processing time of tasks assigned to the regular worker, who is working at the same workstation. Constraints (10), (11), and (12) define the completion time for the whole group of tasks allocated to a multi-manned workstation. Constraint (13) represents the domain of the variables.
3. Proposed h-GA and Computational Results
As MO-MALW-a-BP is an NP-hard problem, metaheuristic approaches are required [13]. For this reason, h-GAs have been developed to find the best solution. The general structure of the proposed h-GA is based on the following three fundamental stages:
- 1.
- Representation scheme and creation of initial population:A genetic representation, based on random keys inspired by Bean [14], is used at this stage to construct a set of solutions representing the initial population . Each chromosome is made up of genes representing tasks, where each assigned value determines the order in which they are processed. This technique guarantees that the predecessors of the tasks are respected.
- 2.
- Fitness evaluation and selection:The proposed method is divided into two distinct stages to optimize task allocation and workload distribution in manned workstations.In the first stage, once has been generated, the algorithm allocates tasks by prioritizing the workstation with the largest number of available workers (). In this stage, an additional heuristic based on “shortest processing time ” is applied to select the regular worker with the minimum sum of processing times, who will then be assigned to . To ensure that the constraints of multi-manned workstations are respected, the algorithm determines the start and end times of each assigned task. When the workstation reaches its , the process opens the next workstation.To improve the quality of the generated assignments, a dynamic optimization phase has been integrated into the algorithm at the second stage. This phase is based on an innovative mechanism for reorganizing tasks between workstations, designed to maximize the efficiency of the algorithm while respecting the constraints imposed. The mechanism is based on the following steps:
- Transfer search: A systematic analysis is performed to identify tasks assigned to the largest workstation that could be transferred to the smallest workstation while respecting priority constraints.
- Comparative evaluation: Once the candidate transfers have been identified, a comparative evaluation is performed to determine if the new configuration offers significant improvements over the previous one. If the new reorganization reduces and , the previous configuration is replaced by the new one, which is then stored in memory.
Furthermore, the algorithm applies the “fixed weights approach” [15], ensuring that the normalization constraint is respected. Consequently, the fitness function is defined as follows:Thereafter, to produce a new population, an elite preservation technique [16] is applied to ensure that the best individuals are passed on to the next generation. - 3.
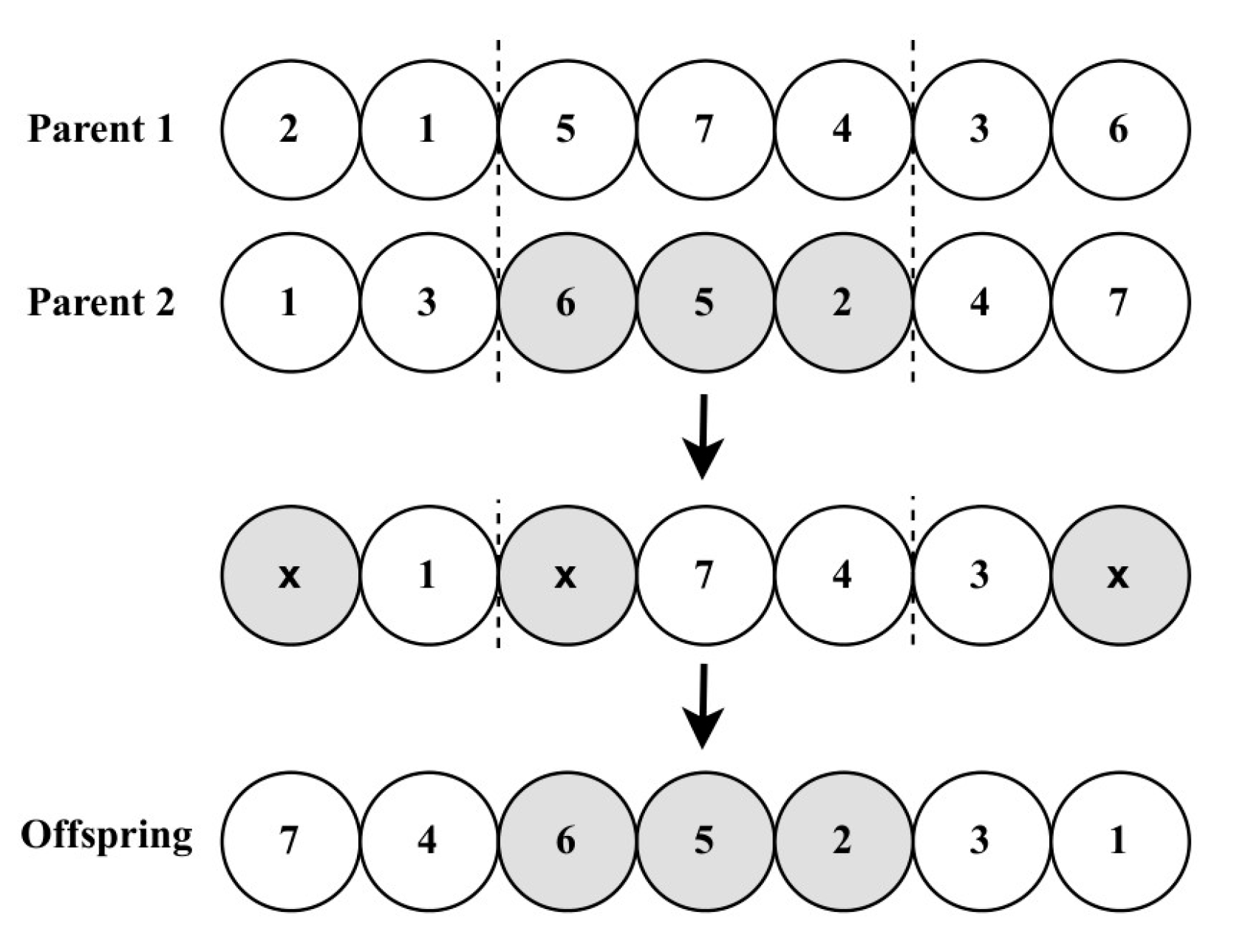
- Crossover and Mutation:To improve the quality of the new population, the cycle crossover (CX) that was originally presented by Oliver et al. [17] is utilized, as shown in Figure 1.
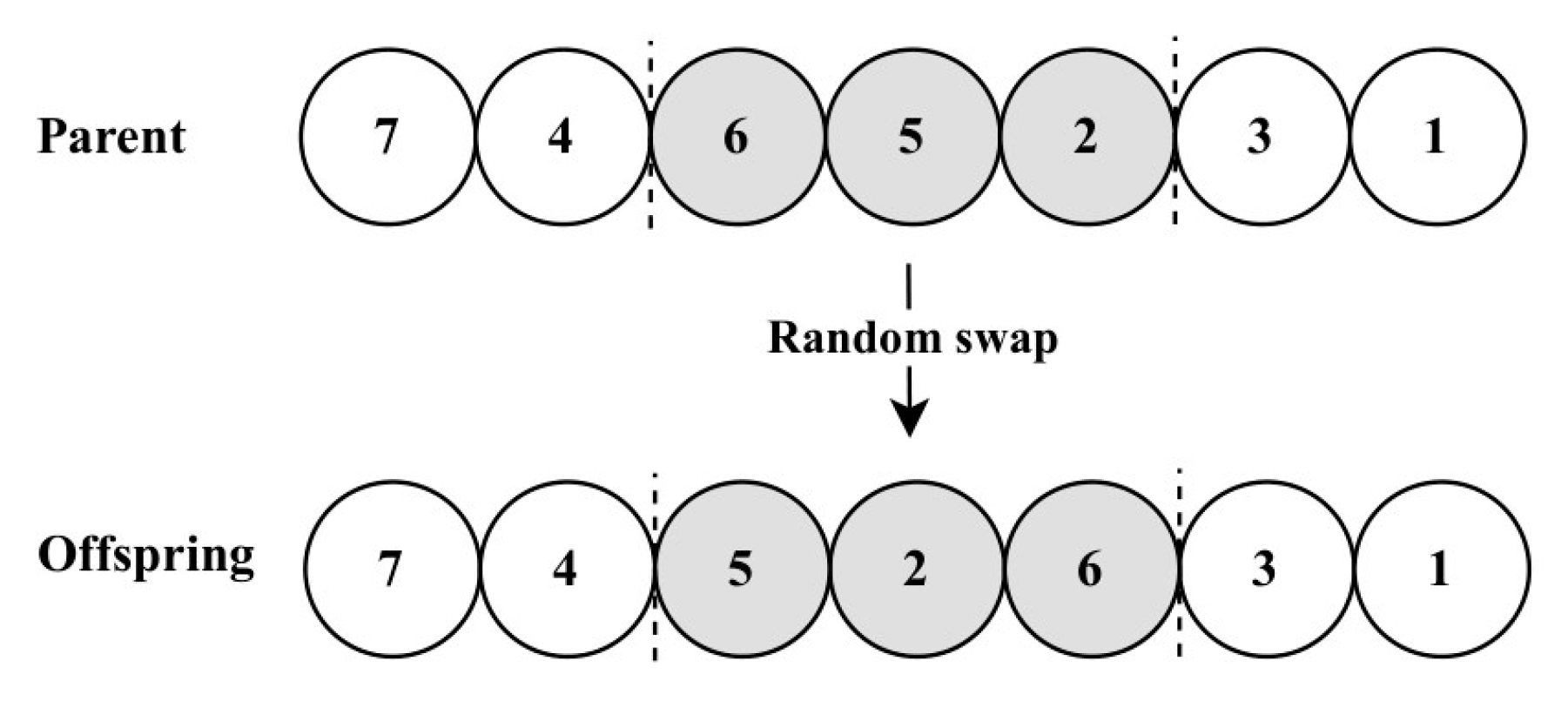
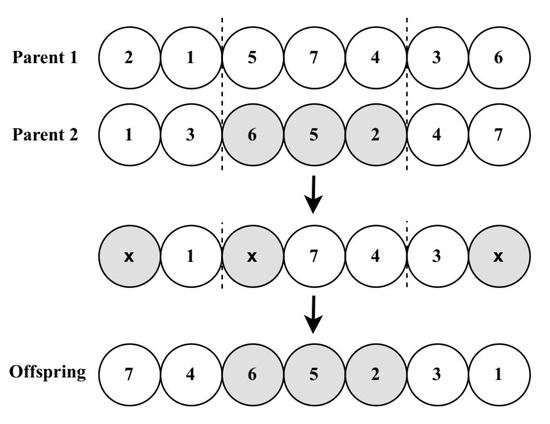 Figure 1. Example of CX.Afterwards, the scramble mutation (SM) is employed, as illustrated in Figure 2, as it was first presented in the context of ALBP by Leu et al. [18]. Following this, the algorithm checks the precedence constraints of the final population to apply Equation (14) and identify the best solution.
Figure 1. Example of CX.Afterwards, the scramble mutation (SM) is employed, as illustrated in Figure 2, as it was first presented in the context of ALBP by Leu et al. [18]. Following this, the algorithm checks the precedence constraints of the final population to apply Equation (14) and identify the best solution.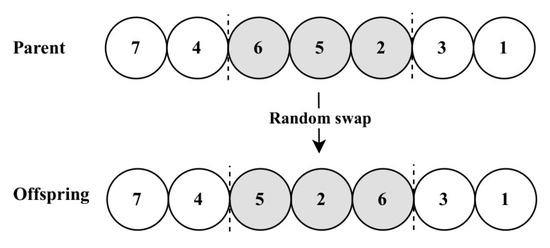 Figure 2. Example of SM.
Figure 2. Example of SM.
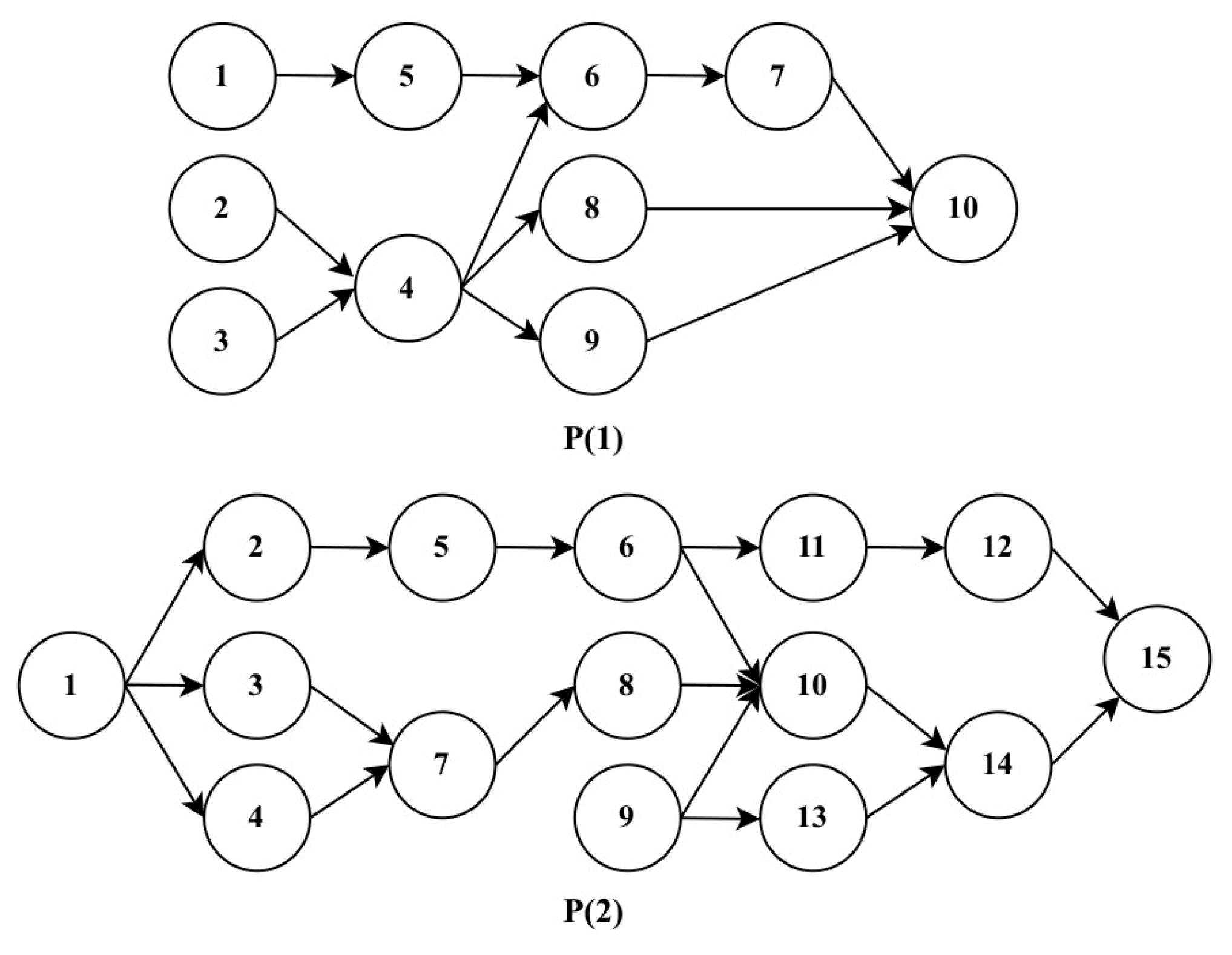
The proposed h-GA is developed in Python 3.13 on a PC with 16 GB RAM. Its effectiveness is evaluated using two numerical examples with . The case study data are illustrated in Table 1 and Figure 3, and the results are compared with those obtained with GA, considering that the algorithm creates a random and calculates using the following Equation (15) [19,20].

Table 1.
Problems data.
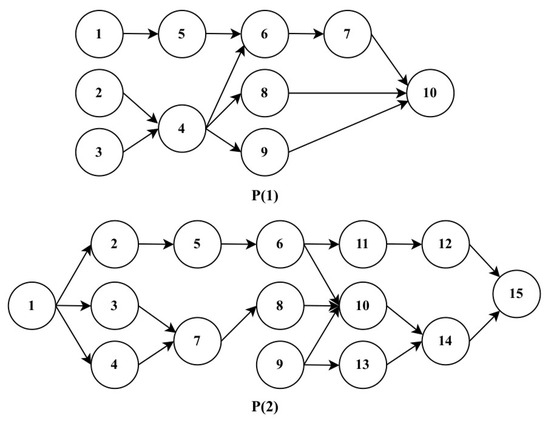
Figure 3.
Precedence graphs for P(1) and P(2).
After obtaining a sequence of tasks respecting the precedence relationships, the GA assigns tasks to workstations until the duration of a workstation exceeds . The parameters used for both algorithms are presented in Table 2.

Table 2.
GA and proposed h-GA parameters.
The previous table (Table 3) shows that both algorithms produce solutions that respect the MO-MALW-a-BP constraints presented in Section 2. However, the proposed method shows a higher efficiency compared to the classical version of GA. For the first problem (P1), which is small, the h-GA produced an optimal solution with compared to for the GA, indicating a perfectly balanced distribution of tasks and optimal utilization of workers. For the second problem (P2), the differences between the two approaches are even more marked. The proposed approach achieves the best solution with , , and , while the classical version of the GA obtains its best solution with , , and .

Table 3.
Results of the proposed h-GA and the GA for P1 and P2.
A comparison of the two approaches clearly demonstrates that the h-GA exhibits higher performance in terms of optimal solutions and stability for scheduling and assigning tasks to manned workstations. This improvement can be attributed to two primary processes integrated into the hybrid approach: (1) task and worker selection heuristics; (2) a dynamic task reorganization mechanism. These combined heuristics promote balanced workload distribution while satisfying multiple objectives. As a result, the proposed h-GA is robust to problems of different sizes and is an effective solution to complex industrial constraints, while ensuring a significant improvement in the productivity of production systems.
4. Conclusions
In this study, the authors proposed a mathematical model to address the MO-MALW-a-BP and demonstrate the effectiveness of the proposed h-GA with two goals: minimizing the cycle time and minimizing the total squared workload. The results show that the proposed approach outperforms the classical version of the GA. The robustness of this approach is based on the integration of heuristics that facilitate the exploration of the search space and the optimal assignment of tasks to workstations.
In future works, the proposed h-GA can be utilized to solve U-shaped issues for MO-MALW-a-BP, taking into account several supplementary constraints.
Author Contributions
Conceptualization, S.E.M. and M.H.; methodology, S.E.M., M.H. and J.E.A.; software, S.E.M. and M.H.; validation, M.H. and J.E.A.; formal analysis, S.E.M.; investigation, J.E.A.; resources, S.E.M.; data analysis, S.E.M.; writing—original draft preparation, S.E.M.; writing—review and editing, M.H.; visualization, S.E.M. and M.H.; supervision, M.H. and J.E.A.; project administration, S.E.M., M.H. and J.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors express their gratitude to the Moroccan Minister of Higher Education, Scientific Research and Innovation, for funding the MENFPESRS/DESRS bilateral R&D project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Batista, L.D.S.; Magatão, L. Multi-manned Assembly Line Balancing Problem in a Diesel Engine Manufacturing Company: A Real-World Case Study. In Intelligent and Transformative Production in Pandemic Times; Huang, C.-Y., Dekkers, R., Chiu, S.F., Popescu, D., Quezada, L., Eds.; Springer: Cham, Switzerland, 2023; pp. 535–543. [Google Scholar]
- Zhang, Z.; Chica, M.; Tang, Q.; Li, Z.; Zhang, L. A multi-objective co-evolutionary algorithm for energy and cost-oriented mixed-model assembly line balancing with multi-skilled workers. Expert Syst. Appl. 2024, 236, 121221. [Google Scholar] [CrossRef]
- Zheng, X.; Ning, S.; Sun, H.; Zhong, J.; Tong, X. Solving multi-objective two-sided assembly line balancing problems by harmony search algorithm based on pareto entropy. IEEE Access 2021, 9, 121728–121742. [Google Scholar] [CrossRef]
- Moreira, M.C.O.; Pastor, R.; Costa, A.M.; Miralles, C. The multi-objective assembly line worker integration and balancing problem of type-2. Comput. Oper. Res. 2017, 82, 114–125. [Google Scholar] [CrossRef]
- Yilmaz, H.; Yilmaz, M. A mathematical model and tabu search algorithm for multi-manned assembly line balancing problems with assignment restrictions. Eng. Optim. 2020, 52, 856–874. [Google Scholar] [CrossRef]
- Hashemi-Petroodi, S.E.; Thevenin, S.; Kovalev, S.; Dolgui, A. Model-dependent task assignment in multi-manned mixed-model assembly lines with walking workers. Omega 2022, 113, 102688. [Google Scholar] [CrossRef]
- Hashemi-Petroodi, S.E.; Thevenin, S.; Kovalev, S.; Dolgui, A. Markov decision process for multi-manned mixed-model assembly lines with walking workers. Int. J. Prod. Econ. 2023, 255, 108661. [Google Scholar] [CrossRef]
- El Machouti, S.; Hlyal, M.; Babay, A.; El Alami, J. Analysis of balancing solutions for simple assembly lines. J. Ind. Eng. Manag. 2024, 17, 828–852. [Google Scholar] [CrossRef]
- Kellegöz, T. Balancing Lexicographic Multi-Objective Assembly Lines with Multi-Manned Stations. Math. Probl. Eng. 2016, 2016, 9315024. [Google Scholar] [CrossRef]
- Tkitek, Z.; Triki, H.; Moalla, H.F. Social sustainability in manufacturing system: Case of multi-manned assembly line. In Proceedings of the 2024 IEEE International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 27–29 April 2024; pp. 1–6. [Google Scholar]
- El Machouti, S.; Hlyal, M.; Babay, A.; El Alami, J. Optimisation of Simple Assembly Line Balancing Problem Type E: A Systematic Literature Review. Manag. Syst. Prod. Eng. 2024, 32, 162–173. [Google Scholar] [CrossRef]
- Azizoğlu, M.; İmat, S. Workload smoothing in simple assembly line balancing. Comput. Oper. Res. 2018, 89, 51–57. [Google Scholar] [CrossRef]
- Belassiria, I.; Mazouzi, M.; ELfezazi, S.; Cherrafi, A.; ELMaskaoui, Z. An integrated model for assembly line re-balancing problem. Int. J. Prod. Res. 2018, 56, 5324–5344. [Google Scholar] [CrossRef]
- Bean, J.C. Genetic Algorithms and Random Keys for Sequencing and Optimization. ORSA J. Comput. 1994, 6, 154–160. [Google Scholar] [CrossRef]
- dos Santos Coelho, L. Multi-Objective Swarm Intelligent Systems: Theory & Experiences; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhang, H.; Yan, Q.; Liu, Y.; Jiang, Z. An integer-coded differential evolution algorithm for simple assembly line balancing problem of type 2. Assem. Autom. 2016, 36, 246–261. [Google Scholar] [CrossRef]
- Oliver, I.M.; Smith, D.J.; Holland, J.R. A study of permutation crossover operators on the traveling salesman problem. In Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and Their Application, Cambridge, MA, USA, 28–31 July 1987; pp. 224–230. [Google Scholar]
- Leu, Y.-Y.; Matheson, L.A.; Rees, L.P. Assembly Line Balancing Using Genetic Algorithms with Heuristic-Generated Initial Populations and Multiple Evaluation Criteria. Decis. Sci. 1994, 25, 581–605. [Google Scholar] [CrossRef]
- El Machouti, S.; Hlyal, M.; El Alami, J. A Hybrid Reactive GRASP approach for the balancing of a mixed-model assembly line of type E with worker allocation. Sci. Afr. 2024, 26, e02378. [Google Scholar] [CrossRef]
- Nourmohammadi, A.; Fathi, M.; Ng, A.H.C. Balancing and scheduling assembly lines with human-robot collaboration tasks. Comput. Oper. Res. 2022, 140, 105674. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).