Definition of Optimal Ephemeris Parameters for LEO-PNT †
Abstract
1. Introduction
2. Analysis of LEO Orbital Elements
3. Ephemeris Computation
3.1. Ephemeris Fitting Algorithm
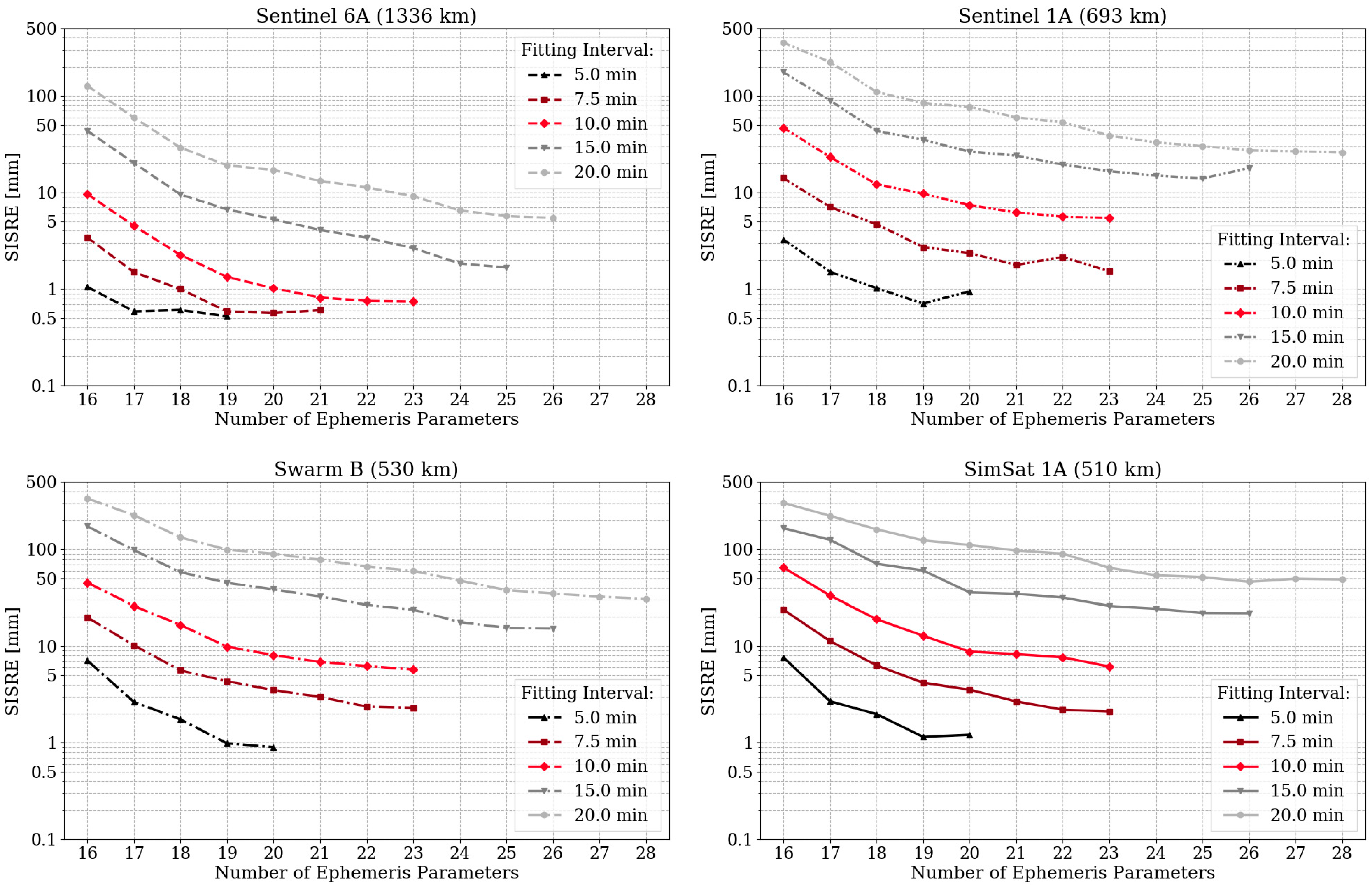
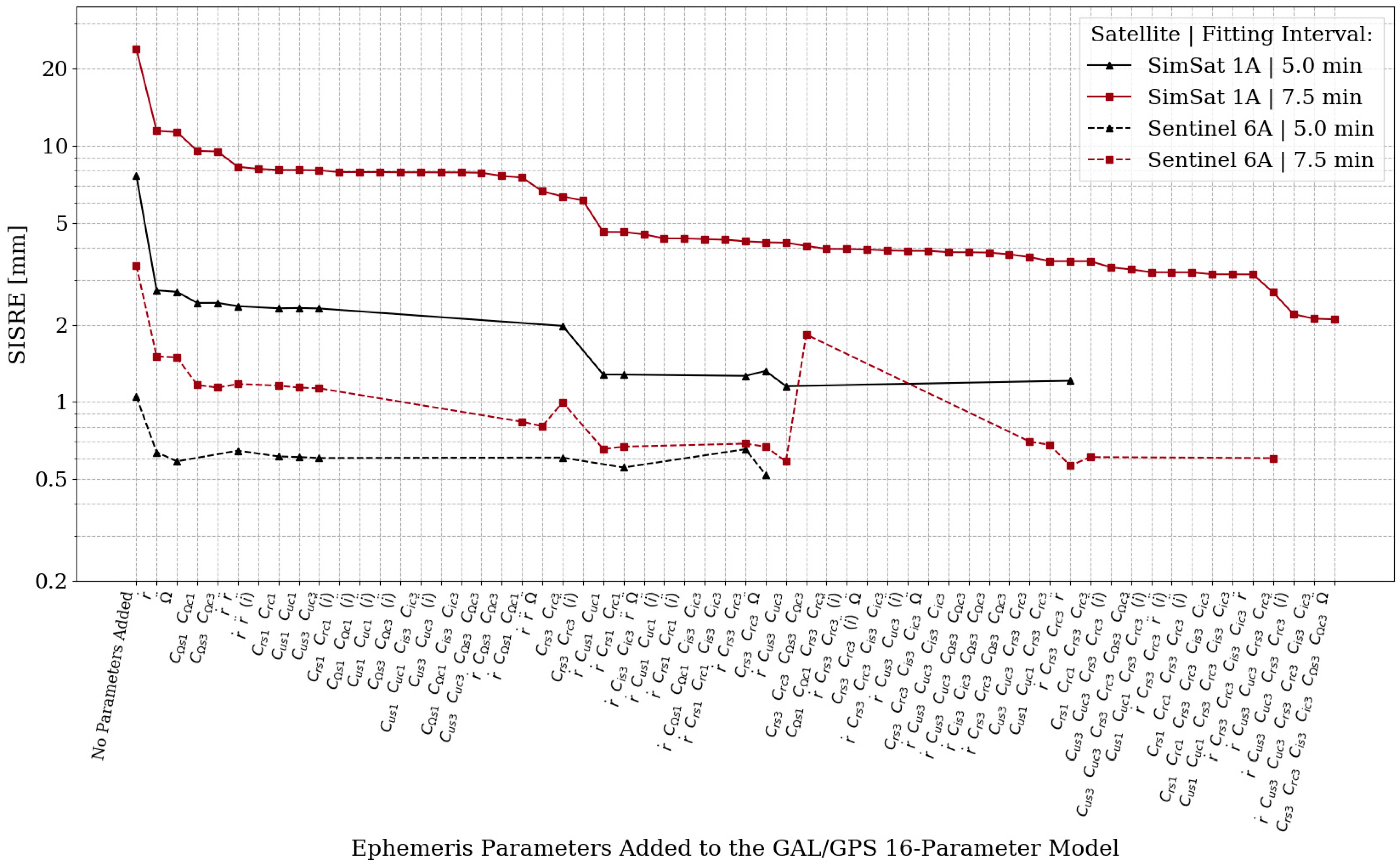
3.2. Results of LEO Optimization Analyses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; Geng, T.; Zhao, Q.; Liu, X.; Zhang, Q.; Liu, J. Design and validation of broadcast ephemeris for low Earth orbit satellites. GPS Solutions 2018, 22, 54. [Google Scholar] [CrossRef]
- Guo, X.; Wang, L.; Fu, W.; Sou, Y.; Chen, R.; Sun, H. An optimal design of the broadcast ephemeris for LEO navigation augmentation systems. Geo-Spat. Inf. Sci. 2022, 25, 1–13. [Google Scholar] [CrossRef]
- NAVSTAR Global Positioning System. NAVSTAR GPS Space Segment/Navigation User Segment Interfaces–Rev. N.; National Coordination Office of the United States: Washington, DC, USA, 2022.
- European GNSS Agency. Galileo Open Service—Signal-in-Space Interface Control Document (OS SIS ICD)—Issue 2.1; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- Fernández, J.; Fernández, C.; Berzosa, J. MAORI—A new Flight Dynamics and Geodesy library. In Proceedings of the 29th International Symposium on Space Flight Dynamics, ESOC, Darmstadt, Germany, 22–26 April 2024. [Google Scholar]
- Gómez, C.; Auz, A.; Monreal, A.; Muñoz, A.; Catalán, C.; Juez, A. Comparison of Different Parametrizations to Minimize the Ephemeris Fitting Error for LEO Satellites. In Proceedings of the 37th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2024), Baltimore, MD, USA, 16–20 September 2024; pp. 867–886. [Google Scholar]
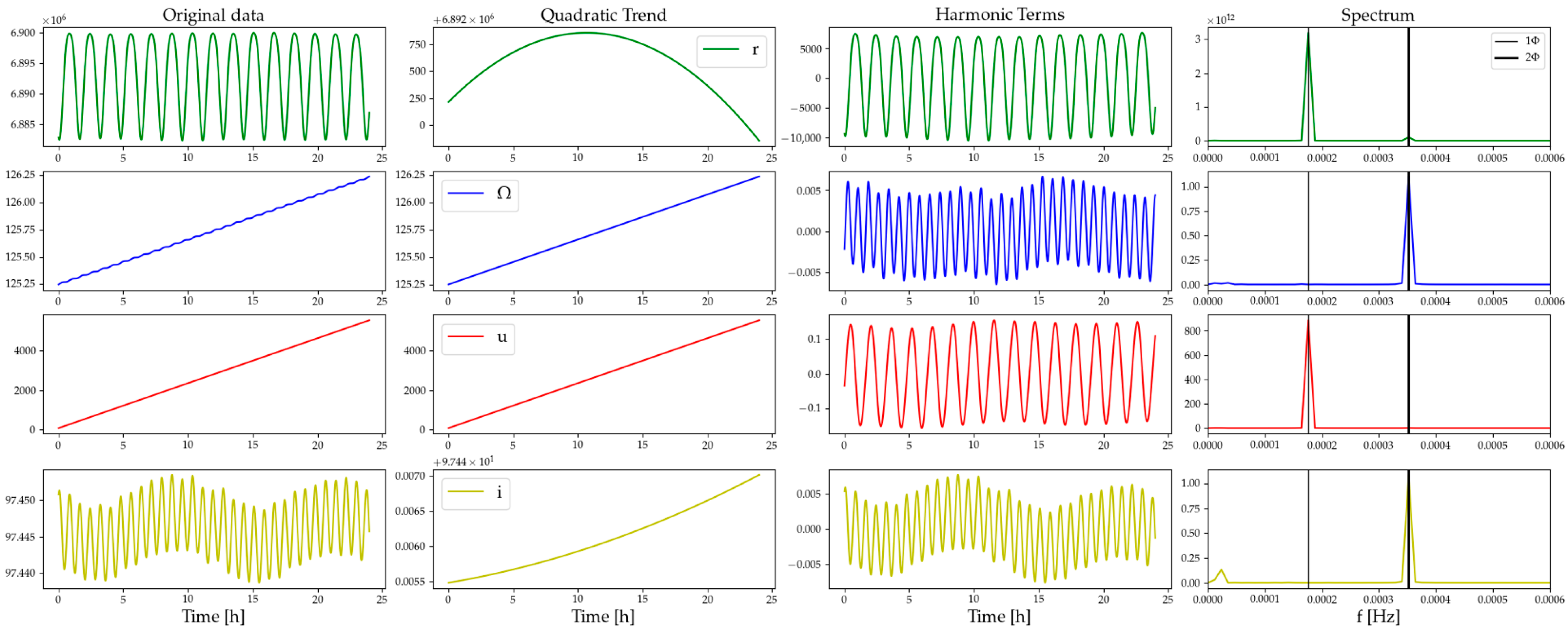
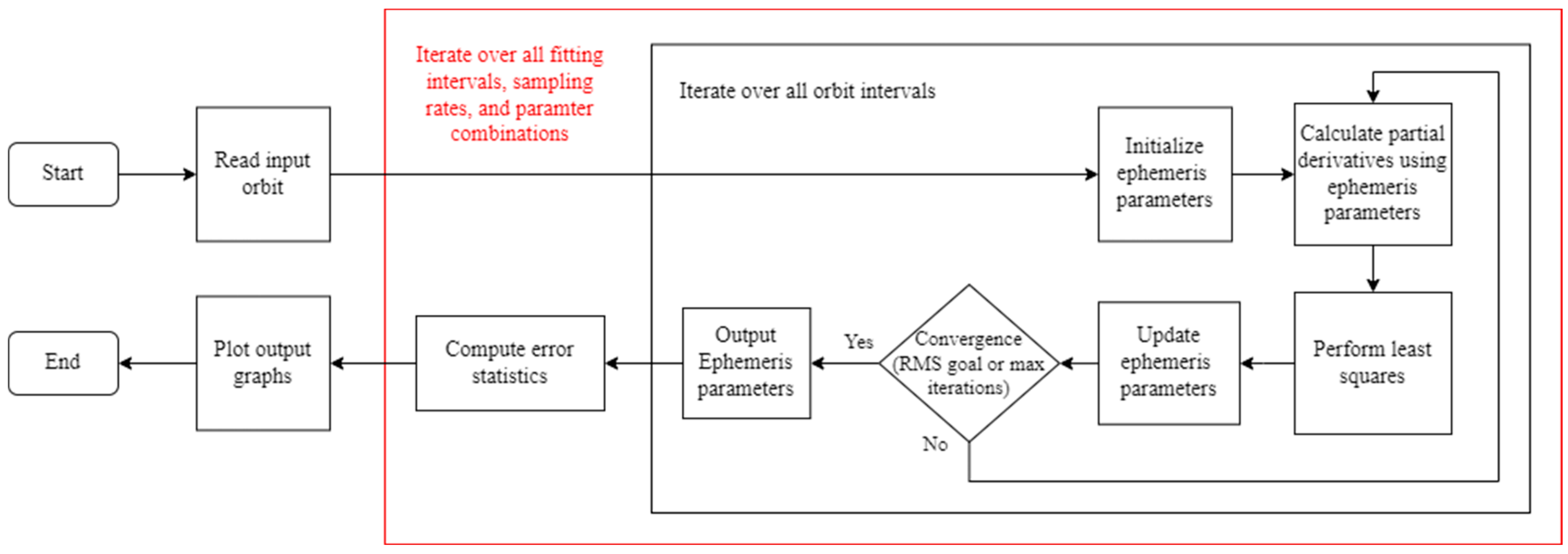
| Parameter | Definition | Parameter | Definition |
|---|---|---|---|
| Square root of the semi-major axis | Eccentricity x-component | ||
| Eccentricity y-component | Mean argument of latitude | ||
| Inclination angle | Right ascension of the ascending node | ||
| Right ascension first-order rate | Inclination first-order rate | ||
| Mean motion difference from computed value | Amplitudes of the 2nd sine and cosine harmonic corrections to the orbital radius * | ||
| Amplitudes of the 2nd sine and cosine harmonic corrections to the argument of latitude * | Amplitudes of the 2nd sine and cosine harmonic corrections to the inclination angle * | ||
| Ephemeris reference time |
| Parameter | Definition | Parameter | Definition |
|---|---|---|---|
| Orbital radius first-order rate | Argument of latitude first-order rate | ||
| Amplitudes of the 1st sine and cosine harmonic corrections to the orbital radius * | Amplitudes of the 1st sine and cosine harmonic corrections to the argument of latitude * | ||
| Amplitudes of the 1st sine and cosine harmonic corrections to the inclination angle * | Amplitudes of the 1st sine and cosine harmonic corrections to the RAAN * | ||
| Amplitudes of the 2nd sine and cosine harmonic corrections to the RAAN | Amplitudes of the 3rd sine and cosine harmonic corrections to the orbital radius ** | ||
| Amplitudes of the 3rd sine and cosine harmonic corrections to the argument of latitude ** | Amplitudes of the 3rd sine and cosine harmonic corrections to the inclination angle ** | ||
| Amplitudes of the 3rd sine and cosine harmonic corrections to the RAAN ** | Orbital radius second-order rate | ||
| Argument of latitude second-order rate | Inclination second-order rate | ||
| Right ascension second-order rate |
| Force Model | Value | Force Model | Value |
|---|---|---|---|
| Gravity field | EIGEN.GRGS.RL04 TVG (100 × 100), drift/annual/semi-annual linear terms up to 90 × 90. | Ocean tides | FES2014 (100 × 100, 100 tidal constituents) |
| Solid Earth tides | IERS 2010 | Earth and ocean pole tides | IERS 2010 |
| Relativity | IERS 2010 | Third bodies | Sun, moon, planets DE-421 |
| Atmospheric density model | msise00 | Drag coefficient | Fixed to 2.0 |
| Fitting Interval | No. of Param. | Parameter Combination Added | SISRE [mm] | No. of Param. | Parameter Combination Added | SISRE [mm] |
|---|---|---|---|---|---|---|
| Sentinel 6A | Sentinel 1A | |||||
| 5 min | 19 | 0.52 | 19 | 0.70 | ||
| 7.5 min | 20 | 0.56 | 23 | 1.52 | ||
| 10 min | 23 | 0.74 | 23 | 5.41 | ||
| 15 min | 25 | 1.67 | 25 | 13.95 | ||
| 20 min | 26 | 5.43 | 28 | 25.50 | ||
| Swarm B | SimSat 1A | |||||
| 5 min | 20 | 0.90 | 19 | 1.15 | ||
| 7.5 min | 23 | 2.30 | 23 | 2.19 | ||
| 10 min | 23 | 5.73 | 23 | 5.77 | ||
| 15 min | 26 | 15.26 | 26 | 21.06 | ||
| 20 min | 28 | 30.73 | 26 | 47.18 | ||
| Fitting Interval Length | Parameter Combination | Approximate SISRE at WUL | |
|---|---|---|---|
| Sentinel 6A | SimSat 1A | ||
| 20 min | 5 mm | 50 mm | |
| 15 min | 2 mm | 20 mm | |
| 10 min | 0.7 mm | 7 mm | |
| 7.5 min | 0.6 mm | 3.5 mm | |
| 5 min | 0.5 mm | 1.3 mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navajas, C.G.; Gómez, A.A.; Muñoz, A.M.; Catalán, C.C.; Muñoz, A.J. Definition of Optimal Ephemeris Parameters for LEO-PNT. Eng. Proc. 2025, 88, 64. https://doi.org/10.3390/engproc2025088064
Navajas CG, Gómez AA, Muñoz AM, Catalán CC, Muñoz AJ. Definition of Optimal Ephemeris Parameters for LEO-PNT. Engineering Proceedings. 2025; 88(1):64. https://doi.org/10.3390/engproc2025088064
Chicago/Turabian StyleNavajas, Carlos Gómez, Aitor Auz Gómez, Alejandro Muñoz Muñoz, Carlos Catalán Catalán, and Andrés Juez Muñoz. 2025. "Definition of Optimal Ephemeris Parameters for LEO-PNT" Engineering Proceedings 88, no. 1: 64. https://doi.org/10.3390/engproc2025088064
APA StyleNavajas, C. G., Gómez, A. A., Muñoz, A. M., Catalán, C. C., & Muñoz, A. J. (2025). Definition of Optimal Ephemeris Parameters for LEO-PNT. Engineering Proceedings, 88(1), 64. https://doi.org/10.3390/engproc2025088064






