Optimised Signal Selection Algorithm for Acquisition and Re-Acquisition in Multi-Constellation, Multi-Frequency GNSS Receivers ^†

Abstract

Acquiring and tracking multiple frequencies across many GNSS satellites introduces computation complexity, resulting in higher power consumption. A relatively small but optimal list of signals and satellites may result in better performance without adding additional complexity load and unnecessary power loss. This research intended to generate an optimal list of satellites and signals and to prioritise them to be tracked by the receiver, minimising unnecessary processing. To achieve this, an optimal geometry is generated using a bootstrapping algorithm, which also introduces an innovative index to determine what to add to the satellites/signals list to prioritise acquisition and tracking.

1. Introduction

The combination of GPS, GALILEO, GLONASS and BEIDOU constellations can provide superior satellite geometry for a GNSS receiver. Taking 12 satellites into consideration from each constellation, a total of 48 satellites can be visible in an ideal RF propagation situation. Furthermore, each satellite may broadcast across multi-frequency bands, which enables precise navigation solutions. For optimal performance, as a rule of thumb, it is not an ideal approach to discard or to stop using the visible set of satellite measurements, if the receiver supports all of them. But when it comes to minimizing system complexity and managing a power budget, there is an obvious challenge to balance performance and power management, as it may not be possible or even necessary to acquire and track everything visible to the GNSS receiver. Therefore, optimised satellite and signal selection is useful not only in obtaining a reliable PVT (position, velocity and time) solution, but also in optimising the power consumption.

Multiple approaches exist, mainly to select or reject measurements from a set of visible satellites that are either not healthy or have large propagation errors. This means selecting M number of satellites from a set N number of visible satellites. This is achieved by using elevation masking to avoid newly-risen satellite(s), and the tightest integrity bound using ARAIM/RAIM ([advanced] receiver autonomous integrity monitoring).

In traditional receivers, the aforementioned methods are employed to select and/or reject measurements obtained after the tracking and data demodulation stage in the GNSS receiver. But in order to obtain redundant measurements, a significantly large number of tracking channels are required, which increases the processing load. Position accuracy is mainly influenced by DOP (dilution of precision) and UERE (user equivalent range rrror), and hence these two parameters should be used in selecting the best subset of satellites from visible satellites [1,2]. Aimlessly tracking all satellite/signals may provide good PVT performance but at the cost of computation complexity and power consumption. The approach described in this paper is to develop an optimised satellite and signal selection algorithm that works in partnership with acquisition and re-acquisition, and still maintains a good PNT performance. Before discussing the research in detail, some of the key approaches are discussed to cover their advantages and disadvantages. Then in an experimental data campaign to verify and validate the proposed algorithm, GNSS signals were collected at baseband in a dense, complex and highly dynamic multipath environment, as discussed in Section 3.

1.1. Elevation Dependent Selection Approach

Elevation dependent satellite selection is the simplest approach. It is very useful, if the receiver manufacturer introduces a significantly high number of tracking channels. The combination of a simpler algorithm and significantly large number of processing trackers can be useful for applications that require significant horizontal position accuracy. In [3], GPS, GLONASS, GALILEO, BDS-2 and BDS-3 constellations were selected to achieve good visibility of satellites for kinematic PPP (precise point positioning). According to the work presented in [3], elevation masks below 25⁰ have very little effect on horizontal position accuracy. However, the vertical accuracies were marginally effective during a long-run test. Furthermore, TTFF (time to first fix) improved when elevation masking above 20⁰ was applied with quick fixing of integer ambiguities. This approach seems ideal for kinematic PPP but not for high integrity applications. The work in [3] discussed the importance of having measurements using lower elevation satellites. If the elevation angle is used as a discriminator approach, then it is recommended to use the almanac to find the approximate satellite location. Along with a rough position estimate, elevation can then be estimated. The receiver can then make the decision to avoid tracking satellites whose elevation angle decreases below the desired elevation masking. The next section discusses an SBAS-based approach for satellite selection that reduces the number of tracking channels to achieve a decent navigation solution.

1.2. SBAS Based Satellite Selection for Multi-Contellation

The work in [4] emphasizes the selection of signals/satellites rather than relying on a large number of tracking channels. SBAS (space based augmentation system) signals are potentially good candidates to identify the most important satellites to track and to recommend to a multi-constellation receiver [4]. The work in [4] also presented how an SBAS-based selection approach can help in achieving greater availability, with greater flexibility in receiver design. This can help the receiver manufacturer make decisions to select a more reliable algorithm or to add more tracking channels with a simpler algorithm. The SBAS-based algorithm also found key weaknesses in elevation-weighted or elevation masking based approaches. Masking lower elevation satellites is not always reliable for applications that require tight vertical integrity. VPL (vertical protection level) is severely affected by worst case VDOP when relying only on high elevation satellites [4].

1.3. Optimal DOP Selection Approach

In late 1980, there were a few proposed approaches for satellite selection using GDOP (geometric dilution of precision). The objective was to improve the PVT accuracy using a minimal number of satellites, also known as the optimal subset of satellites. The concept of an optimal GDOP approach involves obtaining the minimum GDOP using a subset of satellites selected from the set of all visible satellites. It is found that there is high correlation between GDOP and the volume of tetrahedrons, as given in equation [5].

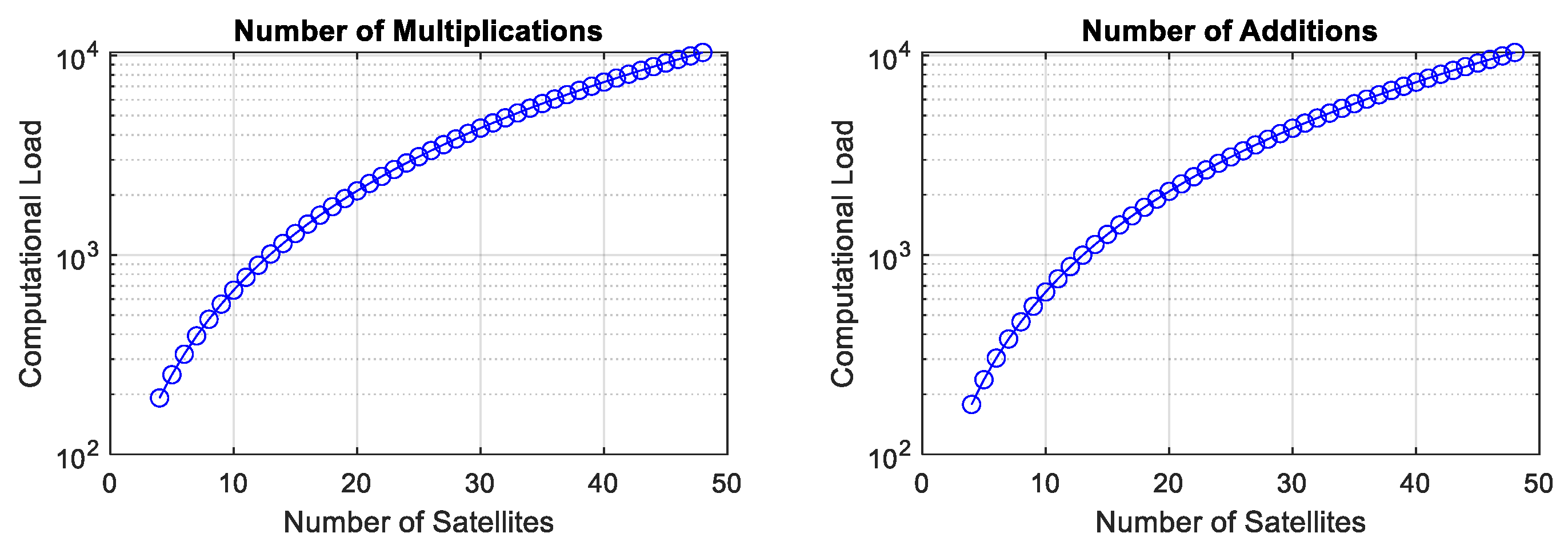
Figure 1 shows the number of additions and multiplications required to estimate a position solution as a function of the number of satellites. It can be clearly seen that computational complexity increases with the number of satellites in the navigation model for a single frequency. This can be even more complex if we select a multi-frequency navigation model. Therefore, reducing the number of satellites to an optimal number is required, which improves not only the computation load, but also the power consumption associated with the computational load. The above illustration is for the navigation solution. The computations required for signal acquisition and tracking are not included, as they depend upon the digital signal processing architecture in the receiver. However, it is conclusive enough to say that the number of satellites adds computational complexities not only to the navigation model but also to the digital signal processing.

In [6,7], a quasi-optimal satellite geometry from a combination of GNSS and/or space- or ground-based augmentation systems was presented. In this method, there is a dependency on the augmentation system. The proposed study does not require any augmentation system. In [8], elevation and azimuth angle constraints are formulated using GEO and IGSO-based navigation constellations with numerical simulation presented using NavIC (Navigation Indian Constellation). The algorithm is based on unsupervised learning-based satellite selection. In [9], machine learning based on signal classification and weighting factors was introduced. Elements of weighting factors include standard deviation of pseudorange, C/No and elevation and azimuth angle. The proposed research also classified LOS (line-of-sight) and NLOS (non line-of-sight) signals to distinguish the signals degraded due to multipaths.

The above literature review covers a wide range of algorithms, selecting either a simpler algorithm with a high-end receiver or a complicated algorithm with a simple receiver. Some of the algorithms, as discussed in [8,9], are complex. This includes machine-learning approaches, which are beneficial, but practical implementation in a receiver is very challenging and can end up in draining a lot of power, which is not suitable for many applications. Considering the hardware challenges, and maintaining a good balance between performance and power consumption, an optimised signal/satellite selection algorithm for acquisition and re-acquisition in a MCMF frequency GNSS receiver is proposed. The proposed algorithm is discussed in detail in Section 2.

2. Optimised Signal/Satellite Selection Algorithm for Acquisition and Re-Acquisition in MCMF Frequency GNSS Receiver

QinetiQ’s Q40 receiver is a multi-constellation, multi-frequency small form factor GNSS receiver based on ASIC (application-specific integrated circuit) technology. Like any traditional receivers, prior to achieving a navigation solution, the receiver is required to acquire and track MCMF GNSS signals, in order to generate measurements for the PVT engine. With multi-constellation and multi-frequency capability in Q40, the obvious challenge is to track power consumption, as it may not be possible or even necessary to acquire and track everything. Therefore, signal/satellite selection and prioritisation is required. A simple data flow diagram showing how satellites/signals can be generated is shown in Figure 2. IDM (interference detection and mitigation) and AS (anti-spoofing) blocks are required to deal with interference and spoofing threats and mitigation. Due to sensitivity issues, the details of IDM and AS are out of the scope of the proposed algorithm. Figure 2 illustrates the data flow from a host user to the main software. The impact of signal/satellite selection can be seen at various processing stages of the receiver, which is discussed later in this section.

The processing stages of the receiver in the time domain can be classed as: COLD_START; WARM_START; HOT_START; and IDEAL. Receiver processing in the COLD/WARM/HOT start state happens once, before the receiver is running ideally. However, the receiver may lose its lock on the SVs. If this happens, then the receiver enters into the re-acquisition mode. The initialised list of signal/satellite is updated at various stages to make sure we obtain an optimised list of signals and satellites. It contains modules to detect whether a signal is under threat due to interference or spoofing. It is very important to achieve an optimal list of satellites based on optimal satellite geometry, which can be derived based on prior information obtained from either ephemeris or the almanac. The proposed concept is not possible for a receiver in COLD_START operation. For the estimation of optimal satellite geometry, we use some of the concepts proposed in [6], modified to improve the feasibility of practical implementation in hardware and software. The following steps are required to get an optimal list of satellites, noting that this is limited to GPS and GALILEO for this explanation:

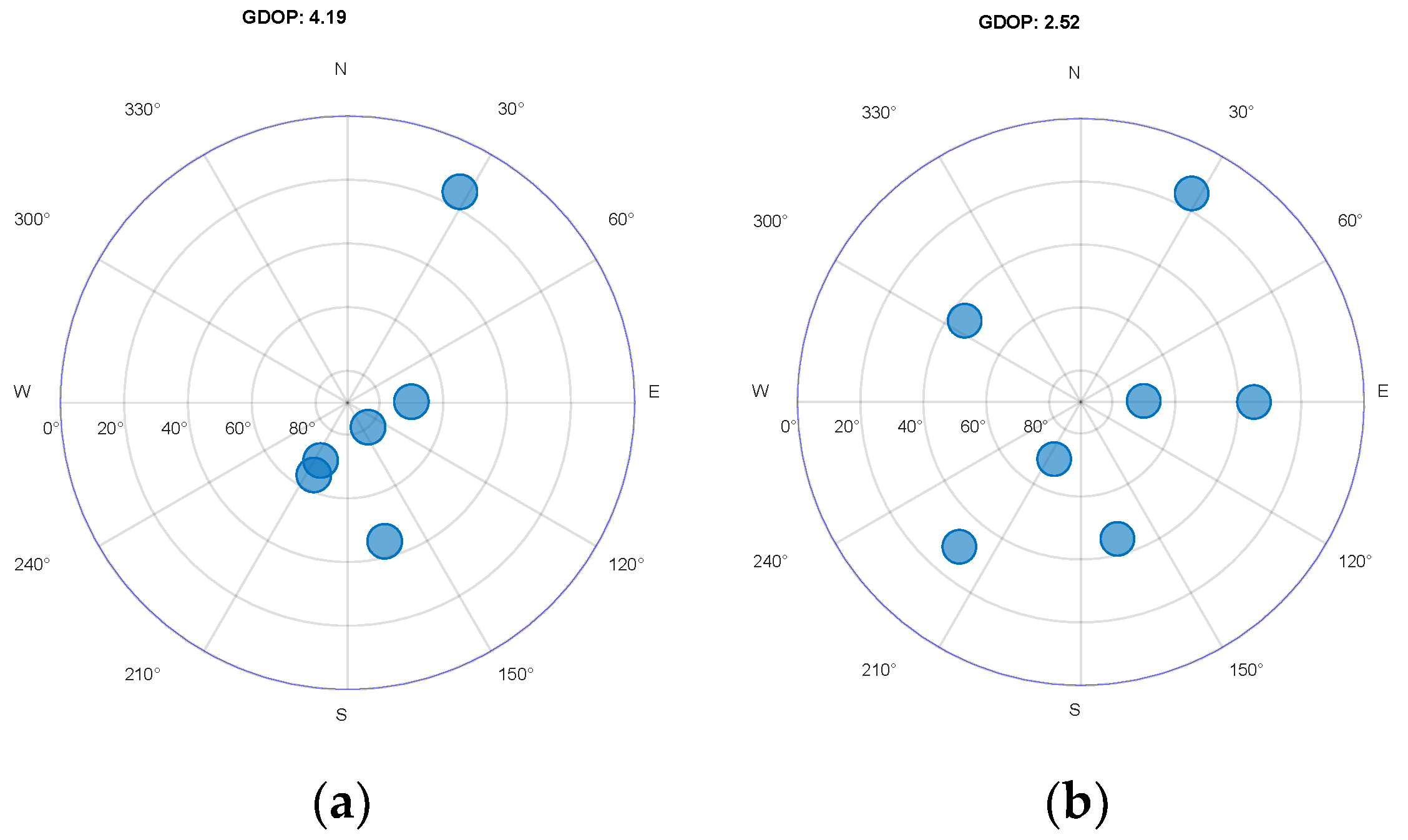
• Using ephemeris/almanac and a rough receiver’s position (precise accuracy not required) derived at time (t_i − 1), compute SVs elevation and azimuth angles. In [10], the number of satellites at zenith is estimated using a lookup table for optimal GDOP. Based on the simulation results in Figure 3, the optimal GDOP does not vary much, even when there are multiple satellites present in the zenith area of the circle. We set the elevation to 60° to represent satellites in the zenith circle, dividing azimuth into multiple sectors and selecting the set of satellites in each sector with a Euclidian distance of more than the threshold. Figure 3a shows the Venn diagram of the zenith circle excluded satellite, which is within the threshold and ignored. Figure 3b shows 12 satellites in view and the zenith circle contain five satellites, which is selected down to three sets of satellites. The combination of non-zenith satellites is achieved using [6]. The GDOP seems very close using just eight satellites, compared to 12 satellites.
• Sort satellites with their elevations in descending order.$S=[S_1, S_2,\dots ,S_N]$ is $N\times 1$ vector. N is the number of SVs. If elevation masking is applied, then the S vector reduces to a new dimension $\left(N-noRejectedSatellite\right)\times 1$.
• Decide the number of satellites at zenith, $S=[S_1, S_r,S_{r+1}\dots ,S_N]$. The blue color font represents zenith satellites (condition defined in step 1). Then re-arrange S to indicate zenith and non-zenith satellites.
• The zenith set of satellites are S₁ and S_r, but if S₁ and S_r have similar azimuth and elevation angles, then only one is selected out of [S₁, S_r]. Otherwise we are left with $S^{\prime }$ as given below:

  $$S^{\prime }={\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{S}_{r+1} \\ ⋮\\ S_{N-1}\end{array}\end{array}\\ S_N\end{array}\right]}_{(N-r)\times 1}$$

  (1)
• Group the other satellites according to their azimuths. Define $t$ as the grouping threshold.
• Estimate the difference between azimuths of the ith satellite and zenith threshold i.e., 60 degrees. Test the condition to generate the kth group of satellites, $\left|\mathsf{\Delta }{a}_i-k\left({\displaystyle \frac{360}{n-r}}\right)\right|\le t\times 2;\Rightarrow S_i ϵ k.$ If the condition is met, then the ith satellite belongs to the kth group, t = 120° is fixed as in [6]. The varying t does not contribute much, and based on simulation results, it is fixed to 120°.
• Select one satellite from every group and combine it with the satellites selected in the 9th step, and then form a subset.
• Down-select the subset(s) with GDOP < 3. In cases where the down-selected list is more than one, then the set with minimum GDOP is selected. GDOP < 3 is considered to be a very good rating, which can help in obtaining high precision and reliable solutions for en route navigation.
• In case of loss of lock, the process of re-acquisition continues until the receiver works in an ideal state. The re-acquisition process requires selection of both satellite and signals for quicker acquisition times. This is achieved by initialising the following potential band of signals: L1 band (includes GPS and GALILEO); L5 band (includes GPS and GALILEO); L2 band (GPS only); L1 band (GPS only); and L1 band (GALILEO only). Estimate the potential acquisition time of the above band of signals for the selected optimal list of satellites.
• Using the acquisition time of all the potential band of signals, estimate an optimised weighting factor, which includes time of acquisition and DOP. A set with the minimum weighting factor is considered to be the final list of signals and satellites to be acquired and tracked.
• The acquisition control settings can be used to estimate how long it will take to acquire all of the signals of a specific type. Assuming that there are 32 PRNs to be acquired, the total time required will be approximately $T=32\times N_F\times N_T\times t_p$; where $N_F$ is the number of frequency passes; $N_T$ is the number of time passes; $t_p$ is the total time required per pass; and $t_p=t_c+N_I\times t_I$.
• Where $t_c$ is the coherent correlation time, $N_I$ is the maximum number of incoherent iterations; $t_I$ is the time between incoherent iterations. Therefore assume that the total time required is calculated as: $T=32\times N_F\times N_T\times \left(t_c+N_I\times t_I\right)$
• The total time required for acquisition would be shorter than if acquisition attempts were terminated early because a strong signal had been found, but would be longer if passes had to be repeated because large peaks were detected.
• However, the above process for an optimal set will be triggered only if there are more than 10 SVs.

3. Experimental Setup and Data Campaigning

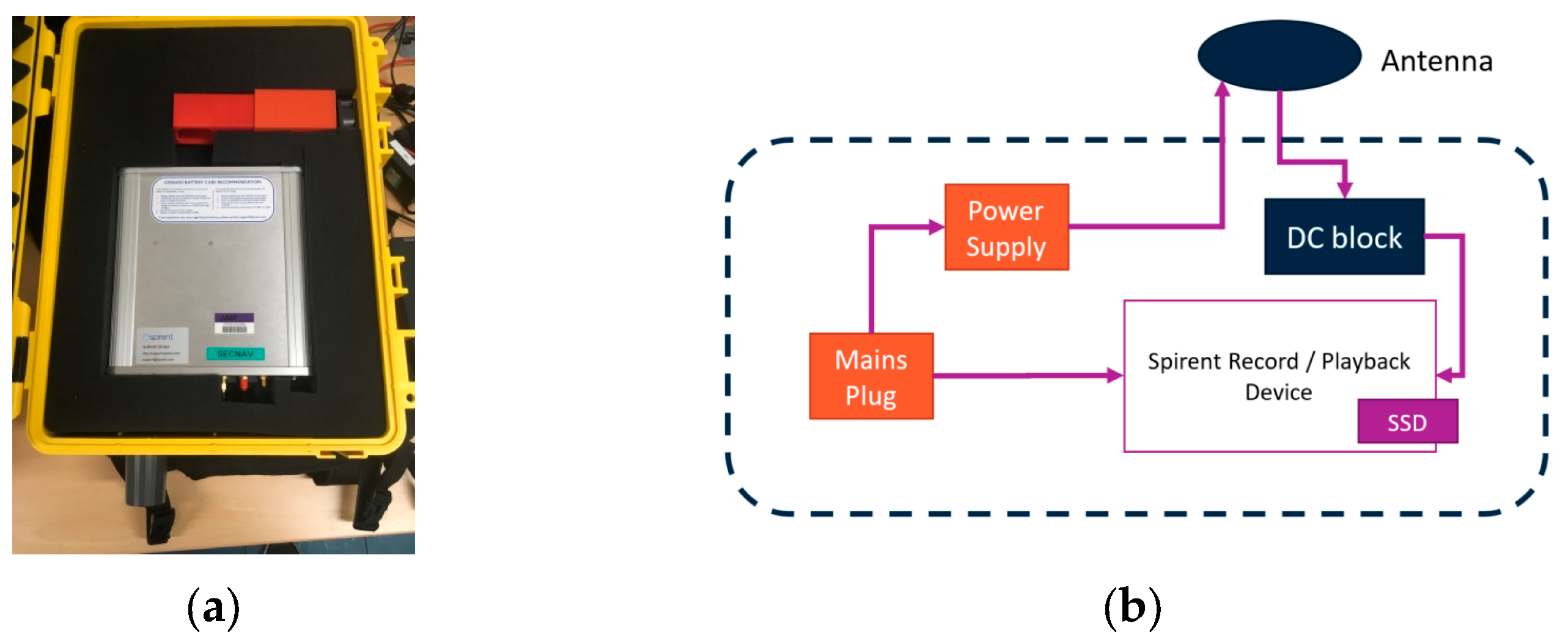
The RF record/playback device is a Spirent model GSS6450, as shown in Figure 4a. The test setup plan (as shown in Figure 4b) is in a van for a dynamic test data campaign. The GSS6450 is able to capture GNSS and other RF signals within the same frequency range from live-sky transmissions. Recorded RF data can be saved as I/Q data to either an internal SSD (solid state drive) or a removable, external SSD. Up to four different GNSS signal bands can be recorded simultaneously, and once captured they can be replayed at any time, allowing for repeatable tests to be performed on GNSS receivers within the lab. The Spirent is able to record and play back up to four GNSS frequency bands (each of which may include multiple GNSS signals from different constellations at similar frequencies) at once. These recordings have a maximum bit-depth of 16 bits and a bandwidth of up to 80 megahertz (MHz). The list of signal bands on the record/playback device are: BEIB1-GLOL1; GPS: L2+GLOL2; Gal: E5+Bei; and B2. The bandwidth used is 50 MHz with bit depth of 8, and low gain selected.

For the dynamic test data campaign, a route was strategically planned to cover short-range tunnels, multiple flyovers, and high-rise buildings causing signal blockages, leading to the degradation of the navigation solution and even complete loss of lock. The data was processed using the innovative approach, the results of which were the prompt re-acquisition of services and notable reduction in re-acquisition time. A route along the M4 motorway approaching Heathrow Airport has been laid out to record GNSS signals received by vehicles travelling on it at higher speeds (70 mph).

4. Results and Discussion

Using GNSS IQ RF collected during the data test campaign, as discussed in Section 3, Skyviews were generated using a Fast Satellite Selection algorithm [6] and the proposed algorithm for comparison. Figure 5a shows the generated Skyview as an optimal generation using a lookup table (in [6]) for optimal GDOP geometries out of 12 SVs. Figure 5b shows the Skyview of a selected set of satellites, where satellites in the zenith circle were not decided by the lookup table, but rather by focusing on the selection of the zenith set of satellites where they are uniformly distributed and estimated using Euclidian distance. The GDOP obtained using the proposed algorithm has improved significantly. The satellite geometry obtained using the proposed algorithm was further used to generate a list of signals to acquire and track right after the loss of lock, using the approach discussed in Section 2. The potential list of satellites yielding good GDOP not only makes acquisition and tracking quicker, but also reduces the usage of tracker channels.

Figure 6a shows a Google satellite street view with the navigation solution, and Figure 6b shows a three dimensional position with the number of locked satellites for cases where a vehicle enters into the tunnel and after the tunnel near Heathrow Airport. After coming out of the tunnel, the navigation solution was retrieved within 0.67 s after clear LOS signals were available by using the optimal satellite/signal selection list rather than asking the tracker to track all SVs and frequencies. In the re-acquisition case, the primary objective was to regain PVT, which then can be improved either using all-view sky satellites if high performance is selected, or otherwise continuing with the same set of optimal satellites/signals if a low-power consumption mode is required. 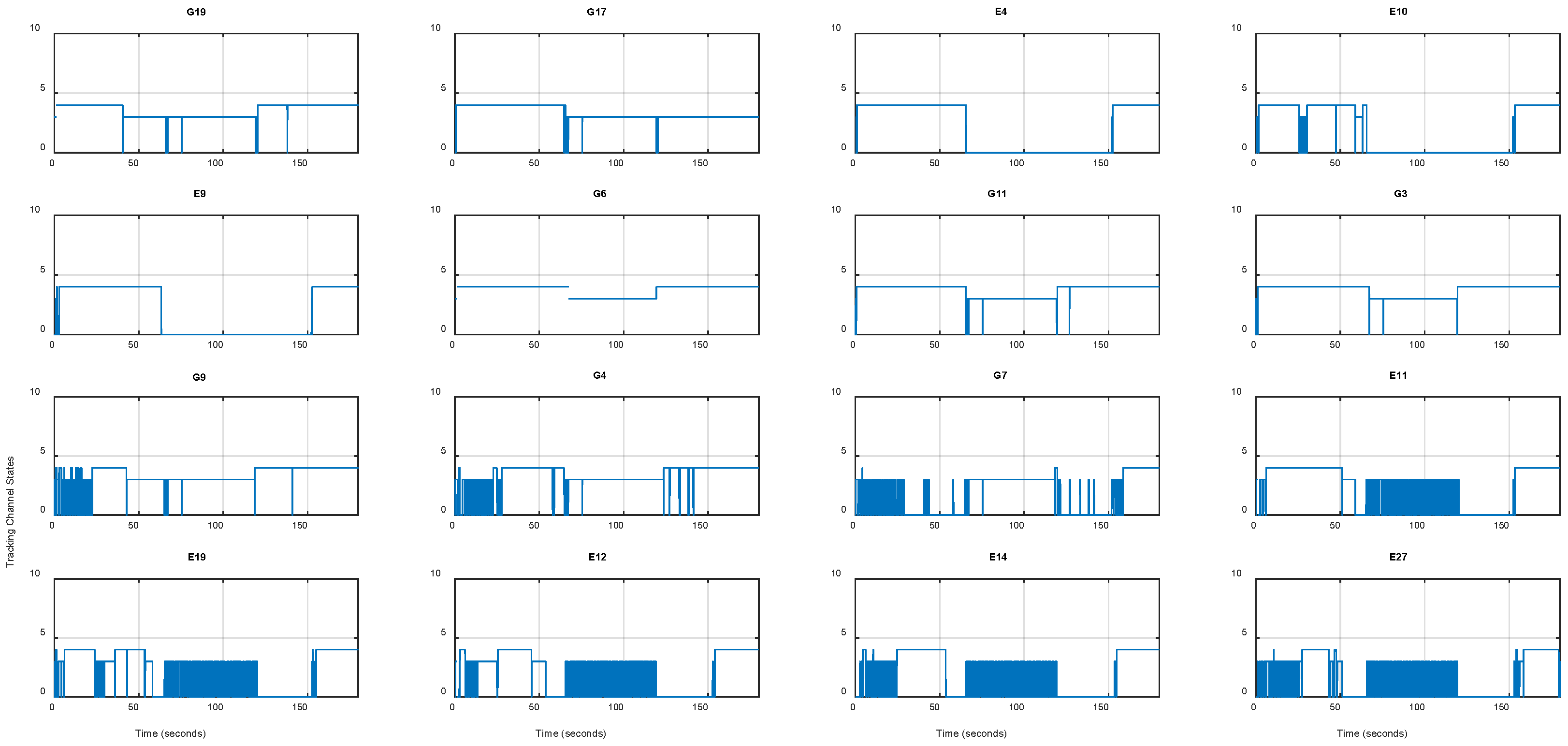Figure 7 shows the tracker status of the receiver. Zeroes indicate that the tracker lost the signal.

5. Conclusions

An optimal satellite/signal list helps in selecting an optimal number of trackers, which helps not only in easing power consumption but also in improving availability. The proposed optimised signal selection algorithm for acquisition and re-acquisition in a MCMF GNSS receiver senses an interference and spoofing threat, and updates if the threat cannot be mitigated, which is achieved prior to generating any optimal list of signals/satellites. This is mainly to avoid any untrusted signals/satellites feeding into the optimal list. The proposed algorithm does not require any look up table to generate a number of zenith and non-zenith satellites, but rather a uniformly distributed list of satellites in a zenith circle are planned first, and then other non-zenith satellites are added to form an optimal satellite geometry. The results show better satellite geometry and quicker re-acquisition of satellites/signals using the optimal list of satellites and signals.