Abstract
In this study, we introduce a decentralized architecture aimed at enhancing the efficiency of precise point positioning real-time kinematics (PPP-RTK) in large-scale networks with a common pivot station. Initially, we partition the extensive network into multiple smaller subnetworks (SNs), each with a common pivot station. The augmentation parameters for each SN are then computed using the precise orbit corrections and ionosphere-weighted constraints. However, directly applying the estimated augmentation parameters to users across subnetworks poses challenges due to inter-subnetwork discontinuities. These discontinuities arise from variations in the network configurations and the time correlation of the Kalman filters, despite the use of the same pivot station. To address this, common augmentation parameters, such as the satellite clocks and phase biases from each SN, are integrated into a unified set of parameters and broadcast to users. The aligned common augmentation parameters are then fed back into each SN, and the Kalman filter is re-updated to mitigate the inter-subnetwork discontinuities. The proposed architecture offers a reduced computational burden compared to the centralized PPP-RTK architecture, which handles a full-scale network simultaneously. Unlike previous research on decentralized PPP-RTK, the use of a common pivot station ensures a consistent basis for the common augmentation parameters. This approach enables seamless user positioning during transitions between SNs, eliminating the need to reset the user navigation filter during handover operations and simplifying the integration process. To evaluate the effectiveness of our proposed architecture, we gather dual-frequency global positioning system (GPS) observation data from over 40 continuously observed reference stations (CORSs) in Korea. These data are then partitioned into four SNs, each sharing a common pivot station. Subsequently, we compare the static positioning error and processing time of our proposed architecture with those of the centralized architecture. Additionally, the mitigation performance of the inter-network discontinuities is shown.
1. Introduction
A navigation system relying on code observations from the global navigation satellite system (GNSS) can provide users with worldwide positioning accuracies within several meters [1]. While this level of accuracy satisfies the requirements for many typical applications, it may not suffice for the navigation performance demands of autonomous driving platforms [2]. To obtain sufficient accuracy for such applications, carrier-observation-based positioning methods are recommended owing to their advantageous characteristics, including their shorter wavelengths and lower noise levels.
Two widely used methods for achieving high-precision positioning are precise point positioning (PPP) and real-time kinematics (RTK) [3,4,5,6]. PPP provides users with the satellite clock, phase, and code biases, providing coverage spanning thousands of kilometers and accuracies within tens of centimeters. However, it typically requires a lengthy convergence time, often extending to tens of minutes [3,4]. However, RTK can achieve positioning accuracies of a few centimeters with rapid convergence times by mitigating most errors in code and phase observations through differencing the base and rover stations. Nonetheless, it faces challenges such as high communication loads and limited coverage within a 50 km radius, as it requires full observation data from a reference station [5,6].
In this context, precise point positioning real-time kinematics (PPP-RTK) emerges as a promising integration of PPP and RTK, attracting significant attention [7,8]. PPP-RTK shares similarities with PPP but introduces ambiguity resolution. This enhancement enables the provision of ionospheric and tropospheric delays at specific grid points or reference stations to multiple users. Consequently, PPP-RTK achieves shorter convergence times than PPP and offers broader coverage compared to RTK. Unlike RTK, the augmentation parameters in PPP-RTK are generated in a state-space representation (SSR) format, significantly reducing the communication loads. However, to provide precise parameters, a service provider must process a large number of reference stations, resulting in a substantial computational load [9,10].
The considerable computational load can cause significant latency and degrade the positioning performance [11]. To address this issue, Hou et al. developed a decentralized approach for PPP-RTK [12]. This divides the entire reference station network into several smaller subnetworks (SNs) and independently processes the augmentation parameters within each SN. Subsequently, the common augmentation parameters among the SNs, including the satellite clocks, phase biases, and code biases, are integrated and re-updated within each SN. Decentralized PPP-RTK has demonstrated improved processing times compared to conventional centralized PPP-RTK while maintaining positioning accuracy. However, users must re-initialize the navigation filter to estimate the phase bias and differential code bias (DCB) during inter-network operations. This requirement arises from the absorption of the pivot station’s DCB in each SN by user ionospheric delays, DCBs, and phase biases.
In our approach, we implement a process similar to conventional decentralized PPP-RTK, with each SN utilizing a common pivot station. Since the pivot station remains consistent across all the SNs, the basis for the common augmentation parameters, including those related to the pivot station, is identical. This assumption enables a simpler integration process for the common augmentation parameters by removing the necessity of estimating the inter-network pivot station offset terms, such as the receiver clock biases, phase biases, and code biases. Subsequently, the integrated common augmentation parameters are updated for each SN to eliminate inter-network discontinuities. Additionally, users can maintain continuous positioning performance during inter-network operations without the need for navigation filter re-initialization.
This paper is structured as follows. Section 2 introduces the architecture of the proposed decentralized PPP-RTK and its steps, and Section 3 compares the positioning performance, processing time, and integrated augmentation parameters between the decentralized and centralized architectures, and it also presents the mitigation of the inter-network discontinuities. Finally, Section 4 presents the conclusions drawn from this study.
2. Proposed Decentralized PPP-RTK with Common Pivot Station
The proposed algorithm is illustrated in Figure 1. The algorithm commences with data acquisition and preprocessing. During data acquisition, dual-frequency (C1 and P2) global positioning system (GPS) observations from continuously observed reference stations (CORSs), along with precise orbit and DCB data, are obtained from the international GNSS service (IGS). Preprocessing involves initial state and covariance computation, alongside cycle slip detection and screening. The primary process of the decentralized algorithm is partitioned into three segments: processing the augmentation parameters for each SN, integrating the common augmentation parameters, and re-updating the SN. These processes are detailed in the subsequent subsections.
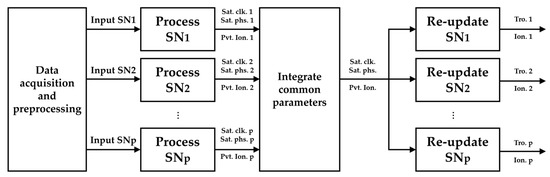
Figure 1.
Architecture of the proposed decentralized PPP-RTK with a common pivot station, where the subscript indicates the index of the subnetwork from 1 to p.
2.1. Processing Augmentation Parameters for Each Subnetworks
The model and methodology for processing the augmentation parameters in each network remains consistent for both the decentralized and centralized PPP-RTK. The estimable parameters of the ionosphere-weighted undifferenced uncombined (IW-UDUC) observation model and the ionospheric constraints are provided by Equations (1)–(3) [12,13].
where and represent the UDUC observed-minus-computed pseudo-range and carrier phase, respectively. denotes an ionospheric pseudo-observation to constrain the difference between pivot stations, ensuring it remains small within a regional network of approximately 200 km. The superscript ‘s’ denotes the satellite index, while the subscript ‘r’, ‘j’ indicate the receiver and frequency indices, and ‘p’ is the index for SN. and represent the zenith wet delay and its global mapping function, respectively, which are used to convert the zenith wet delay into the slant wet delay. and indicate the satellite and receiver clock bias, respectively. is the slant ionospheric delay with respect to the first frequency, and is the ionospheric constant of the jth frequency, defined as . and indicate the satellite and receiver code bias at the jth frequency, respectively, which are estimable only for j > 2. Then, denotes the DCB between the L1 and L2 frequencies. Similarly, and indicate the satellite and receiver phase bias at the jth frequency, respectively. Here, and denote the integer ambiguity and the wavelength of the jth frequency (m), respectively. The detailed notations for the estimable parameters are summarized in Table 1 [12,13]. Notably, as our approach implements dual-frequency observations, the receiver and satellite code biases cannot be estimated.

Table 1.
Estimable parameters for subnetwork processing.
2.2. Integrating Common Augmentation Parameters
Although the pivot stations across the SNs remain consistent, the common augmentation parameters—such as the satellite clocks, phase biases, and ionospheric delay at the pivot station—should be identical, as the terms induced by the pivot receiver are the same. However, the common augmentation parameters between the SNs may contain offsets due to differences in the network configuration and time correlation inherent in the Kalman filters between the SNs. Consequently, an additional process to integrate the common parameters from different networks is required to eliminate the inter-network discontinuities between the SNs. Since the pivot stations are common across the SNs, the basis for the common parameters—such as the pivot receiver clock, DCB, phase delay, and integer ambiguities—remains identical. Then, new estimable parameters for integrating these common parameters can be defined, as illustrated in Table 2.

Table 2.
Re-parameterized estimable parameters for common parameter integration.
The integrated augmentation parameters are denoted as , and can be obtained using weighted least squares that incorporate the common augmentation parameters from each SN.
where represents the design matrix for the integration process, constructed by concatenating the identity matrices corresponding to the dimensions of the pseudo-observation vector across multiple SNs. Meanwhile, denotes the covariance of a pseudo-observation vector, formulated as a block diagonal matrix comprising the state covariance matrices of each SN.
2.3. Re-Updating Subnetwork
After the integration process, the common augmentation parameters are aligned across the SNs. However, the atmospheric delay products, such as tropospheric and ionospheric delays, remain unaligned because the integration process is performed independently of the Kalman filter used in each SN. To align the tropospheric delay within each SN to the integrated common parameters, the Kalman filter of each SN must be re-updated by applying a conditional adjustment using the least squares method, as follows:
where , represent the integrated common augmentation parameters and their covariances, respectively. , and denote the re-updated uncommon terms of the augmentation parameters and their covariance at the SN index of ‘p’, and represents the covariance between the common and uncommon augmentation parameters.
2.4. User Model for the Proposed PPP-RTK
The model for the proposed PPP-RTK user is as follows:
where the subscript ‘u’ represents the index of the user receiver, and ‘intp’ denotes the interpolated parameter. The user’s model is nearly identical to the PPP-RTK server model, but it specifically estimates the user’s position differential vector and the line-of-sight vector from the user to the satellite, . The user first subtracts the integrated satellite clock and phase bias from its UDUC observation and applies the precise orbit data from the server to its broadcasted satellite orbit solution. Next, the ionospheric and tropospheric delays from the server, relative to the reference station or grid point, are interpolated to the user’s position and applied accordingly.
In the original decentralized PPP-RTK, it has been shown that users are required to reset their receiver’s DCB and phase biases when switching ionospheric corrections from one network to another [13]. This issue arises due to differences in the pivot stations used by each network, as the estimable parameter of the ionospheric delay absorbs the DCB specific to the pivot station of the respective network. In contrast, within our proposed architecture, the pivot stations across the SNs are identical, and the common augmentation parameters, including the ionospheric delay at the common pivot station, are integrated and re-updated within the Kalman filter of each SN. As a result, users of the proposed decentralized PPP-RTK do not need to reset their receiver phase bias or DCB during inter-network operations, which ensures continuous positioning performance.
3. Results
To evaluate the performance of the proposed architecture, we collected dual-frequency GPS observation data on DOY207, 2023. The observational data were obtained in receiver independent exchange format (RINEX), with a 1 Hz sampling rate, from various operators, including the National Maritime Positioning, Navigation and Timing (NMPNT) Office’s reference station, the Precise Positioning and Integrity Monitoring (POINT) project’s reference station, and the National Geographic Information Institute (NGII) reference station in South Korea.
Figure 2 shows the 28 CORSs selected for augmentation parameter generation and the 12 test sites. In the decentralized architecture, these 28 CORSs were divided into four SNs, with MOOJ serving as the common pivot station. The coverage for each SN is depicted as a white area in Figure 2. Additionally, the distance from the pivot station (MOOJ) is represented by red dashed lines at 100 km intervals. Then, the CORS configurations for the SNs and test sites are detailed in Table 3. In Table 3, subscript ‘T’ indicates a reference station equipped with a Trimble NetR9 receiver (Trimble Inc., Westminster, CO, USA) with a Trimble TRM59800.00 antenna and SCIS dome. Otherwise, ‘L1’ indicates a reference station equipped with a Leica GR50 receiver (Leica Microsystems, Inc., Wetzlar, Germany) with a Leica LEIAR20 antenna and LEIM dome. In the case of ‘L2’, the reference station is equipped with a Leica GR50 or GR25 receiver with a Leica LEIAR25.R4 antenna and LEIT dome.
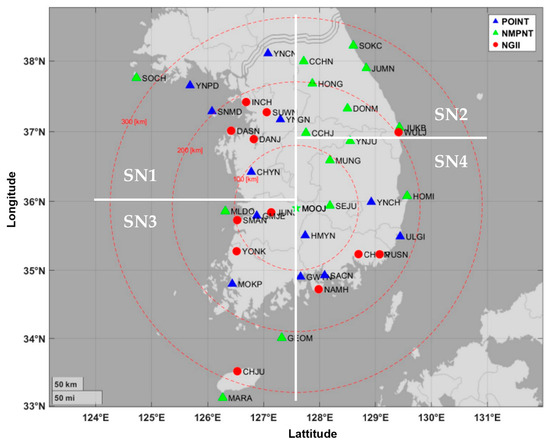
Figure 2.
Location of the 28 CORSs for the SNs (triangle) and 12 test sites (circle).

Table 3.
CORS configurations for each SN and test site.
To process the augmentation parameters, we implement the ambiguity float solution and an ionosphere-weighted model. For both the server and user sides, a satellite elevation cutoff angle of 10 degrees is applied. The time correlation of the individual Kalman filters for the SNs is neglected in this work, and the augmentation parameters are assumed to be provided to the user without latency at a 1 Hz resolution. On the user side, partial ambiguity resolution (PAR) is employed using the least squares ambiguity decorrelation adjustment (LAMBDA) method to resolve integer ambiguities, and the positioning result resolution is 1 Hz. Additionally, the uncertainty of the augmentation parameters on the user side is neglected. Atmospheric augmentation parameters, including the ionospheric and tropospheric delays, are provided to the user relative to the location of the reference station where the augmentation parameters are generated. The user then interpolates these atmospheric augmentation parameters to their approximate position using an inverse distance weighting (IDW) method. The precise positions of the CORSs used for processing the augmentation parameters and evaluating the positioning performance are determined using AUSPOS [14]. The augmentation parameters and user positioning solutions are processed on a computer equipped with an Intel® Core™ I7-13700k CPU (Intel, Santa Clara, CA, USA), 64GB RAM, and MATLAB 2023a.
Figure 3 shows the processing time for both the centralized and decentralized architecture. The mean processing time is highlighted with red dashed line, centralized PPP-RTK is 121.29 ms per epoch, while the decentralized spends 8.19 ms per epoch in each SN. And for the integration, the update sequence took 0.34 ms and 0.15 ms each.
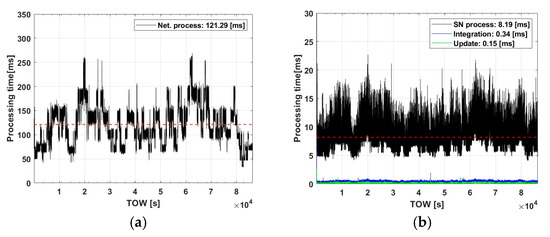
Figure 3.
Processing time: (a) centralized processing and (b) decentralized processing.
Figure 4 shows the difference between the augmentation parameters generated by the centralized and decentralized architectures, which are broadcast to users. Owing to the frequent loss of lock issue of the satellites at a low elevation angle, we plot the satellite with a continuous view over 10 min. Then, Figure 5 compares the horizontal and vertical positioning error of the centralized and decentralized architectures for the DANJ, WULJ station.
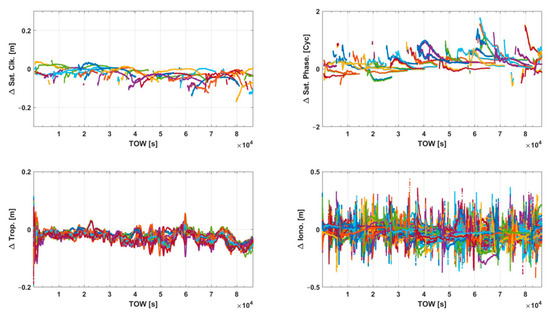
Figure 4.
Differenced augmentation parameters between the centralized and decentralized architectures.
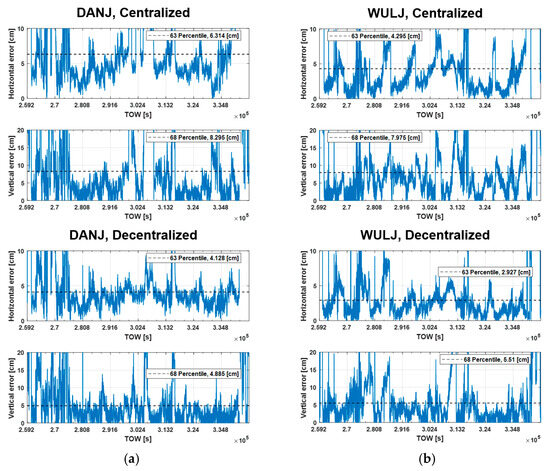
Figure 5.
Positioning result in the time series of the (a) DANJ and (b) WULJ.
Table 4 shows the statistics for the daily horizontal and vertical positioning errors at the test sites for each architecture. The percentage in the decentralized results indicates the reduction in the positioning error compared to the centralized architecture.

Table 4.
Horizontal (63%) and vertical (68%) positioning error for the central and decentralized architectures.
Additionally, we evaluate the mitigation performance of the inter-network discontinuities of the proposed architecture. As shown in Figure 6, the common augmentation parameters between SN1 and the integrated solution are compared with the presence of the re-updating process.
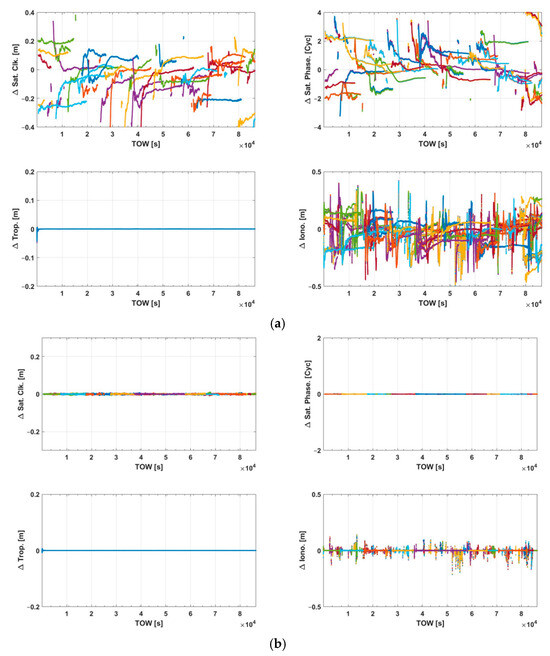
Figure 6.
Differenced augmentation parameters between SN1 and the integrated solution (a) without re-update and (b) with re-update.
4. Conclusions
In this paper, we presented a decentralized PPP-RTK architecture with common pivot stations and compared its results with the conventional centralized PPP-RTK. The proposed architecture has shown a reduction in the processing time per epoch in each network by less than 10% compared to the conventional PPP-RTK. The total processing time of the proposed architecture can be further improved by implementing parallel computation for each SN. Moreover, the static positioning results from 12 CORSs show improved precision with our proposed architecture. However, the difference in the augmentation parameters between the proposed and centralized architectures exhibited non-zero behavior. Although this difference was less than 10 cm for the non-phase terms and approximately less than one cycle for the phase terms, it could be reduced further by applying an ambiguity resolution method, such as LAMBDA, to the augmentation parameter generation. Alternatively, implementing a Kalman filter in the integration process could reduce the noise in the integrated parameters. These issues will be investigated further in our future work.
Author Contributions
Conceptualization, S.P. (Sulgee Park) and S.P. (Sanghyun Park); methodology, C.L.; software, C.L.; validation, C.L.; formal analysis, C.L.; investigation, C.L.; resources, S.P. (Sulgee Park) and C.L.; data curation, C.L.; writing—original draft preparation, C.L.; writing—review and editing, S.P. (Sulgee Park); supervision, S.P. (Sanghyun Park); project administration, S.P. (Sulgee Park); funding acquisition, S.P. (Sanghyun Park). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from the National R&D Project ‘Development of ground-based centimeter-level maritime precise PNT technologies’ funded by the Ministry of Oceans and Fisheries (RS-2020-KS201371).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Angrisano, A.; Gaglione, S.; Gioia, C. Performance assessment of GPS/GLONASS single point positioning in an urban environment. Acta Geod. Geoph. 2013, 48, 149–161. [Google Scholar] [CrossRef]
- Reid, T.G.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization requirements for autonomous vehicles. SAE Intl. J. CAV 2019, 2, 173–190. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current State of Precise Point Positioning and Future Prospects and Limitations. In Observing Our Changing Earth. International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Odolinski, R. Multi-GNSS Integer Ambiguity Resolution Enabled Precise Positioning. Doctoral Dissertation, Curtin University, Perth, Australia, 2015. Available online: https://core.ac.uk/download/pdf/195632004.pdf (accessed on 17 April 2025).
- Odolinski, R.; Teunissen, P.J. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: A low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Hou, P.; Zha, J.; Liu, T.; Zhang, B. Recent advances and perspectives in GNSS PPP-RTK. Meas. Sci. Technol. 2023, 34, 051002. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Shen, Z.; Han, J.; Li, L.; Wang, B. Review of PPP–RTK: Achievements, challenges, and opportunities. Sat. Navig. 2022, 3, 28. [Google Scholar] [CrossRef]
- Hu, J.; Cui, B.; Li, P.; Bisnath, S.; Zheng, K. Exploring the role of PPP–RTK network configuration: A balance of server budget and user performance. GPS Sol. 2023, 27, 184. [Google Scholar] [CrossRef]
- Psychas, D.; Khodabandeh, A.; Teunissen, P.J. Impact and mitigation of neglecting PPP-RTK correctional uncertainty. GPS Sol. 2022, 26, 33. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B. Decentralized GNSS PPP-RTK. J. Geod. 2023, 97, 72. [Google Scholar] [CrossRef]
- Zha, J.; Zhang, B.; Liu, T.; Hou, P. Ionosphere-weighted undifferenced and uncombined PPP-RTK: Theoretical models and experimental results. GPS Sol. 2021, 25, 135. [Google Scholar] [CrossRef]
- Janssen, V.; McElroy, S. A Practical Guide to AUSPOS. In Proceedings of the Association of Public Authority Surveyors Conference, Leura, Australia, 21–23 March 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).