Advanced Receiver Autonomous Integrity Monitoring and Local Effect Models for Rail, Maritime, and Unmanned Aerial Vehicles Sectors †
Abstract
:1. Introduction
2. Architecture
2.1. Rail
2.2. Maritime
2.3. UAVs
3. Methodology
3.1. Rail and Maritime
- Development of the error level monitoring function;
- Development of an FDE;
- Derivation of the multipath models for each error level.
3.2. UAVs
4. Data
4.1. Rail and Maritime
4.2. Data Campaign
- The reference track is created by post-processing a kinematic solution (PPK) and fusing it together with IMU data. The precise orbit and clock files are obtained from NASA’s Archive of Space Geodesy Data through the IGS Multi-GNSS Experiment (MGEX). The PPK is obtained by combining a forward and backward processed solution. The sensor fusion is performed based on a UAV model, which is tuned for high dynamic operations based on a tightly coupled extended Kalman filter. The initial attitude is corrected by means of the dual-antenna GNSS heading obtained directly from the receiver.
- The second set used a reference track created using a private total station with a known position to trace the UAV position throughout each flight. The total station consists of a Leica MS60 multistation which uses a Leica prism reflector mounted on the UAV to determine its position.
5. Results
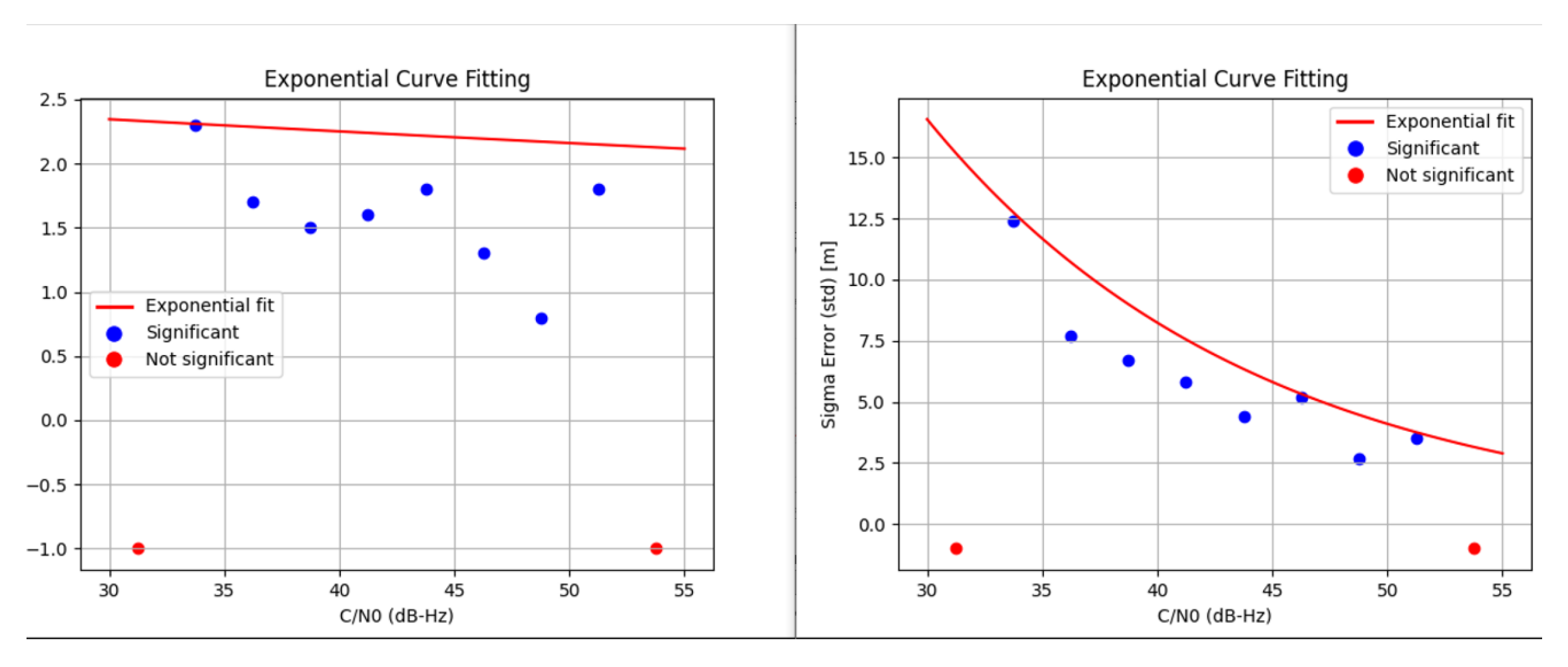
5.1. Rail
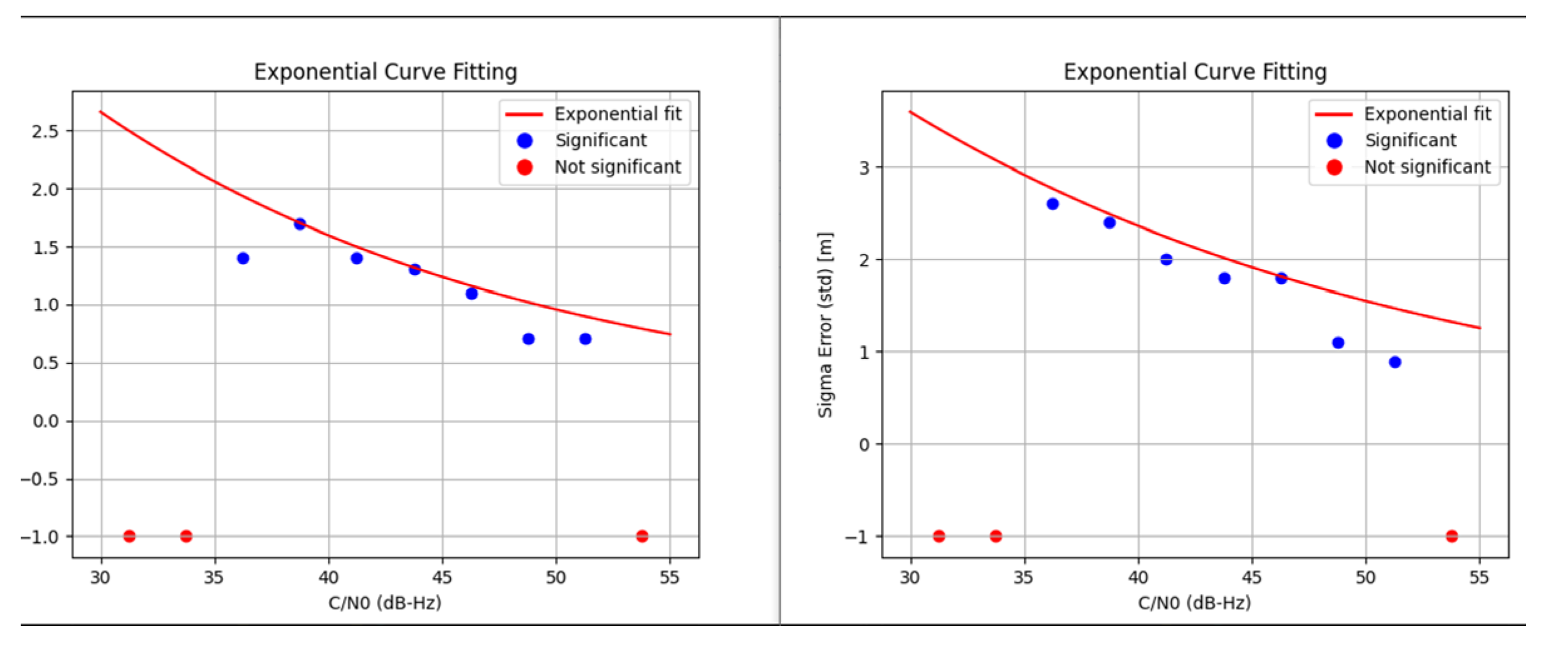
5.2. Maritime
5.3. UAVs
6. Discussions
- For Error Level 1 model in rail, each sigma value is greater than that in maritime due to the deep-urban epochs used in rail that are not present in maritime;
- Best-case models are presented as the data used is insufficient for making safety-of-life models and are the ones closest to those that will be obtained through an extensive data campaign;
- With an extensive data campaign, at least three models must be derived and Error Level 1 samples will be divided into Error Level 1 and Error Level 2.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline Advanced RAIM User Algorithm and Possible Improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Wallner, S.; Fernandez, F.; Dellago, R.; Ioannides, R.; Pervan, B.; Hernandez, I.; Belabbas, B.; et al. Critical elements for a multi-constellation advanced RAIM. Navig. J. Inst. Navig. 2013, 60, 53–69. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P. Framework for analyzing ARAIM architectures. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS), Nashville, TN, USA, 17–21 September 2012; pp. 2850–2857. [Google Scholar]
- RTCA. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment (RTCA DO-229D); RTCA: Washington, DC, USA, 2006. [Google Scholar]
- Fidalgo, J.; Domínguez, E.; Moreno, G.; Buendía, F.; Duque, J.P.; Martínez, J.; Snijders, M.; Engwerda, H.; Burdash, O.; Luciano, A.; et al. ARAIM for Applications Beyond Aviation. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 725–751. [CrossRef]
- Advanced RAIM Reference Airborne Algorithm Description Document (ARAIM ADD), Version 4.1 Draft. Available online: https://web.stanford.edu/group/scpnt/gpslab/website_files/maast/ARAIM_TSG_Reference_ADD_v3.1.pdf (accessed on 31 May 2023).
- Jahn, A.; Bischl, H.; Heib, G. Channel Characterization for Spread Spectrum Satellite Communication. In Proceedings of the IEEE 4th International Symposium on Spread Spectrum, Mainz, Germany, 25 September 1996. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification. Department of Computer Science, National Taiwan University: Taipei, Taiwan, 19 May 2016; Available online: http://www.csie.ntu.edu.tw/~cjlin (accessed on 31 May 2023).
- Wang, Y.; Liu, P.; Liu, Q.; Adeel, M.; Qian, J.; Jin, X.; Ying, R. Urban environment recognition based on the GNSS signal characteristics. Navigation 2019, 66, 211–225. [Google Scholar] [CrossRef]
- Feriol, F.; Watanabe, Y.; Vivet, D. GNSS-based environmental context detection for navigation. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 888–894. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Jozdani, S.E.; Johnson, B.A.; Chen, D. Comparing deep neural networks, ensemble classifiers, and support vector machine algorithms for object-based urban land use/land cover classification. Remote Sens. 2019, 11, 1713. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, G.; Cezón, A.; Moreno, G.; Grant, A.; Shaw, G.; Callewaert, K.; Tavares, T.; Porfili, S.; Ostolaza, J.; Aarmo, K.A. Study of EGNOS V3 Maritime Safety Service. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 1817–1831. [Google Scholar] [CrossRef]
- Natural Resources Canada (NRCan). Online Precise Point Positioning (PPP) Tool. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php (accessed on 14 June 2023).
| Error Level | Output | Pseudorange Error Parameter |
|---|---|---|
| Error 0 | 0 | [0.0, 1.5] m |
| Error 1 | 1 | >1.5 m |
| Precision | Recall | F1-Score | |
|---|---|---|---|
| Error 0 | 0.91 | 0.98 | 0.94 |
| Error 1 | 0.93 | 0.72 | 0.81 |
| Accuracy | - | - | 0.91 |
| Macro Avg. | 0.92 | 0.85 | 0.88 |
| Weighted Avg. | 0.91 | 0.91 | 0.91 |
| Multipath Model Coefficients | |
|---|---|
| Error 0 | ; |
| Error 1 |
| Precision | Recall | F1-Score (95%) | |
|---|---|---|---|
| Error 0 | 0.94 | 1.00 | 0.97 |
| Error 1 | 0.80 | 0.24 | 0.37 |
| Accuracy | - | - | 0.94 |
| Macro Avg. | 0.87 | 0.62 | 0.67 |
| Weighted Avg. | 0.93 | 0.94 | 0.93 |
| Multipath Model Coefficients | |
|---|---|
| Error 0 | ; |
| Error 1 |
| Environment | Min. Multipath (95%) | Max. Multipath (95%) |
|---|---|---|
| Open Sky | 1.5 m | 14 m |
| Semi-Urban | 4.8 m | 23.5 m |
| Urban | 12.6 m | 51.2 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Toro, J.; Sanz, C.; Labrador, E.; Clopot, R.; Mistrapau, F.; Fidalgo, J.; Domínguez, E.; Moreno, G.; Buendía, F.; Cezón, A.; et al. Advanced Receiver Autonomous Integrity Monitoring and Local Effect Models for Rail, Maritime, and Unmanned Aerial Vehicles Sectors. Eng. Proc. 2025, 88, 27. https://doi.org/10.3390/engproc2025088027
de Toro J, Sanz C, Labrador E, Clopot R, Mistrapau F, Fidalgo J, Domínguez E, Moreno G, Buendía F, Cezón A, et al. Advanced Receiver Autonomous Integrity Monitoring and Local Effect Models for Rail, Maritime, and Unmanned Aerial Vehicles Sectors. Engineering Proceedings. 2025; 88(1):27. https://doi.org/10.3390/engproc2025088027
Chicago/Turabian Stylede Toro, Javier, Carlos Sanz, Elena Labrador, Roxana Clopot, Florin Mistrapau, Javier Fidalgo, Enrique Domínguez, Ginés Moreno, Fulgencio Buendía, Ana Cezón, and et al. 2025. "Advanced Receiver Autonomous Integrity Monitoring and Local Effect Models for Rail, Maritime, and Unmanned Aerial Vehicles Sectors" Engineering Proceedings 88, no. 1: 27. https://doi.org/10.3390/engproc2025088027
APA Stylede Toro, J., Sanz, C., Labrador, E., Clopot, R., Mistrapau, F., Fidalgo, J., Domínguez, E., Moreno, G., Buendía, F., Cezón, A., Snijders, M., Engwerda, H., Casals, J., Damy, S., Sgammini, M., & Boyero, J. P. (2025). Advanced Receiver Autonomous Integrity Monitoring and Local Effect Models for Rail, Maritime, and Unmanned Aerial Vehicles Sectors. Engineering Proceedings, 88(1), 27. https://doi.org/10.3390/engproc2025088027






