GNSS Accuracy Under White Gaussian Noise Jamming ^†

Abstract

The jamming of Global Navigation Satellite Systems (GNSSs) is now a major threat for GNSS-based Position, Navigation, and Timing (PNT) users. A jammed receiver will lose its fix at a certain distance and will not be able to provide PNT information. At greater distances, there will be a fix, so this PNT information can be obtained; however, the information will be less accurate, as the carrier-to-noise ($C/N_0$) ratios of the received signals will be suppressed by the jammer. In this paper, the pseudo-range accuracy of a GNSS receiver under jamming conditions is investigated in order to provide more insight into the effects of a jammer on the accuracy of a GNSS receiver. The theory available in the literature will be reviewed, after which this theory will be evaluated by comparing the theoretical results with actual measurements using a high-end GNSS signal simulator and a software-defined GNSS receiver.

1. Introduction

In recent years, there has been a great increase in the occurrence of Global Navigation Satellite System (GNSS) jamming. In conflict areas, GNSS jamming is widely deployed to hamper the operations of the opposing force. A good overview of where jamming occurs in the world is provided by the website “GPSJam.org”. The idea behind GNSS jamming is simple; by causing interference, the jammer increases the noise received at a receiver until the receiver can no longer track the desired signals. As the received GNSS signals are extremely weak, in the order of −155 dBW, a low-power interference source can impact a large area. A jammer with a power of just 20 mW might cause GNSS disruptions in an area with a radius of more than one kilometer, which is a surface area of more than 3 square kilometers. This makes GNSS jamming relatively easy to perform and cheap, and it can have a large impact, as many systems rely on GNSS not only for positioning but even more often because of the accurate timing it provides. For this reason, GNSS jamming is becoming increasingly popular among the military and other state actors, in addition to criminals and other actors. The reasons for the use of a jammer range from privacy protection for individuals to protection from GNSS-guided (cruise) missiles.

The presence of an interference source, such as a jammer, will impact the carrier-to-noise ratio ($C/N_0$). The carrier-to-noise ratio is the ratio between the power of the carrier of the desired signal $C$ to the power spectral density of the (thermal) noise $N_0$. If the $C/N_0$ is suppressed enough, the receiver can no longer track the signals and will lose its lock on these signals. Usually, for Binary Phase Shift Keying (BPSK) signals, such as the Global Positioning System (GPS) C/A code or P(Y) code signals, the threshold where the receiver will lose its lock is around 25 dB-Hz [1]. However, before the lock is lost, the accuracy of the receiver will deteriorate. This is shown in [2] through a practical experiment and some basic calculations made to predict the impact on GPS C/A. Also, in [3], the effect on accuracy is shown in an experimental setup where the accuracy of commercial GPS receivers is assessed under different jamming-to-signal ratios. In the current paper, we delve deeper into the theory behind the impact of a jammer on position accuracy. The focus is on the impact of a Gaussian white-noise jammer with different bandwidths on the GPS C/A code and Galileo E1 signals. As both types of signals are sent using different modulation techniques, with GPS C/A being a BPSK signal and Galileo E1 being a Composite Binary Offset Carrier (CBOC) signal, the effects of jamming are expected to be different.

Theory from the literature will be reviewed, after which this theory will be evaluated by comparing the theoretical results with actual measurements using a high-end GNSS signal simulator and a software-defined GNSS receiver [4].

1.1. Goal of This Paper

The main goal of this paper is to provide insight into the effects of jamming on the accuracy of GNSS receivers. The main message is that the effective range of a jammer is not equal to the range at which the receiver loses its lock; this range is potentially much larger, depending on the required accuracy of the position solution. This paper focuses on the pseudo-range accuracy under additive white Gaussian noise (AWGN) jamming conditions. Biases are not considered. If the accuracy can be predicted well, this prediction can be used to determine the expected effective range of a jammer, in this case, for an AWGN jammer, for applications where accuracy is critical.

1.2. Layout of This Paper

This paper is organized in the following way. First, the theoretical background on which the prediction of the pseudo-range accuracy is based is given. This theoretical background includes the effect of a jammer on the $C/N_0$ and the tracking error of the DLL. Next, the experimental setup is explained, after which the results are provided. Finally, the paper is drawn to a close in the Conclusions.

2. The Impact of a Jammer on DLL Noise

Pseudo-range errors are a result of the tracking error of the delay lock loop (DLL), so this is our starting point. The tracking error for a non-coherent DLL discriminator is given by the general expression [5,6,7]

$${\sigma }_{\tau }^2={\displaystyle \frac{B_L{\int }_{-B_r/2}^{B_r/2}{S}_s\left(f\right){\sin }^2\left(\pi fd{T}_c\right)\mathrm{d}f}{{\left(2\pi \right)}^2\frac{C}{N_0}{T}_c^2{\left({\int }_{-B_r/2}^{B_r/2}f{S}_s\left(f\right)\sin \left(\pi fd{T}_c\right)\mathrm{d}f\right)}^2}}\left[1+{\displaystyle \frac{{\int }_{-B_r/2}^{B_r/2}{S}_s\left(f\right){\cos }^2\left(\pi fd{T}_c\right)\mathrm{d}f}{T\frac{C}{N_0}{\left({\int }_{-B_r/2}^{B_r/2}{S}_s\left(f\right)\cos \left(\pi fd{T}_c\right)\mathrm{d}f\right)}^2}}\right],$$

(1)

where $S_s\left(f\right)$ is the normalized power spectral density of the signal used, $d$ is the correlator spacing, $T_c$ is the duration of a code chip, $T$ is the coherent integration time, $B_L$ is the DLL tracking bandwidth, and $B_r$ is the receiver’s front-end bandwidth. In (1), the noise and interference are assumed to be white Gaussian noise.

In [1], a simplified version of (1), specifically for BPSK signals, is given:

$${\sigma }_{\tau }^2={\displaystyle \frac{B_{L}d{T}_c^2}{2\frac{C}{N_0}}}\left(1+{\displaystyle \frac{2}{T\frac{C}{N_0}}}\right).$$

(2)

As we see in these equations, the accuracy is dependent on the $C/N_0$, amongst other parameters. The $C/N_0$, however, is the only parameter that can be influenced by an interference source, such as a jammer. So, if we can determine the impact of a jammer on the $C/N_0$, we will be able to predict the accuracy of the GNSS receiver while under attack from a jammer.

In the literature, the following expression for the impact of interference with a received power $J$ on the effective $C/N_0$ can be found [7]:

$${\left(C/N_0\right)}_{eff}={\displaystyle \frac{P_{B_r}}{\frac{N_0}{C}+\frac{T_c}{Q}\frac{J}{C}}},$$

(3)

where $P_{B_r}$ is the normalized received power of the desired signal within the bandwidth of the front end of the receiver, and $Q$ is a jamming resistance quality factor. This jamming resistance quality factor can be calculated as follows:

$$Q={\displaystyle \frac{T_c{P}_{B_r}}{{\int }_{-B_r/2}^{B_r/2}{S}_i\left(f\right)S_s\left(f\right)df}},$$

(4)

where $S_i\left(f\right)$ is the normalized power spectral density of the interference; for an AWGN jammer,

$$S_i\left(f\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{B_i}}& \mathrm{f}\mathrm{o}\mathrm{r}-{\displaystyle \frac{B_i}{2}}\le f\le {\displaystyle \frac{B_i}{2}}\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\end{array}\right.,$$

where $B_i$ is the bandwidth of the jammer. Further, the received power, $P_{B_r}$, of the signal is expressed as

$$P_{B_r}=\underset{-B_r/2}{\overset{B_r/2}{\int }}{S}_s\left(f\right)df.$$

The normalized power spectral densities for BPSK and CBOC are expressed as

$$S_{BPSK}\left(f\right)=T_c\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{c}}^2\left(\mathsf{\pi }f{T}_c\right),$$

(5)

and

$$S_{CBOC}\left(f\right)=T_c\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{c}}^2\left(\mathsf{\pi }f{T}_c\right)\left[{\displaystyle \frac{10}{11}}{\tan }^2\left({\displaystyle \frac{1}{2}}\mathsf{\pi }f{T}_c\right)+{\displaystyle \frac{1}{11}}{\tan }^2\left({\displaystyle \frac{1}{12}}\mathsf{\pi }f{T}_c\right)\right].$$

(6)

Finally, the received power of the jammer for the receiver at a distance $R$ can be calculated by using the well-known Friis law, expressed as

$$J=J_0{G}_t{G}_r{\left({\displaystyle \frac{\lambda }{4\pi R}}\right)}^2,$$

where $J_0$ is the transmitted jammer power; $G_t$ and $G_r$ are the antenna gains for the jammer and receiver, respectively; and $\lambda$ is the wavelength.

Upon inspecting (3), it becomes clear that both the duration of a chip, $T_c$, and the jamming resistance quality factor, $Q$, influence the impact of a jammer. A smaller $T_c$ (a larger chiprate) will reduce the impact of a jammer, so the P(Y) code with a chiprate of 10.23 MHz will be less affected by a jammer than a C/A code with a chiprate of 1.023 MHz. This is, of course, exactly as expected. Similarly, a larger $Q$ will also reduce the impact of the jammer. 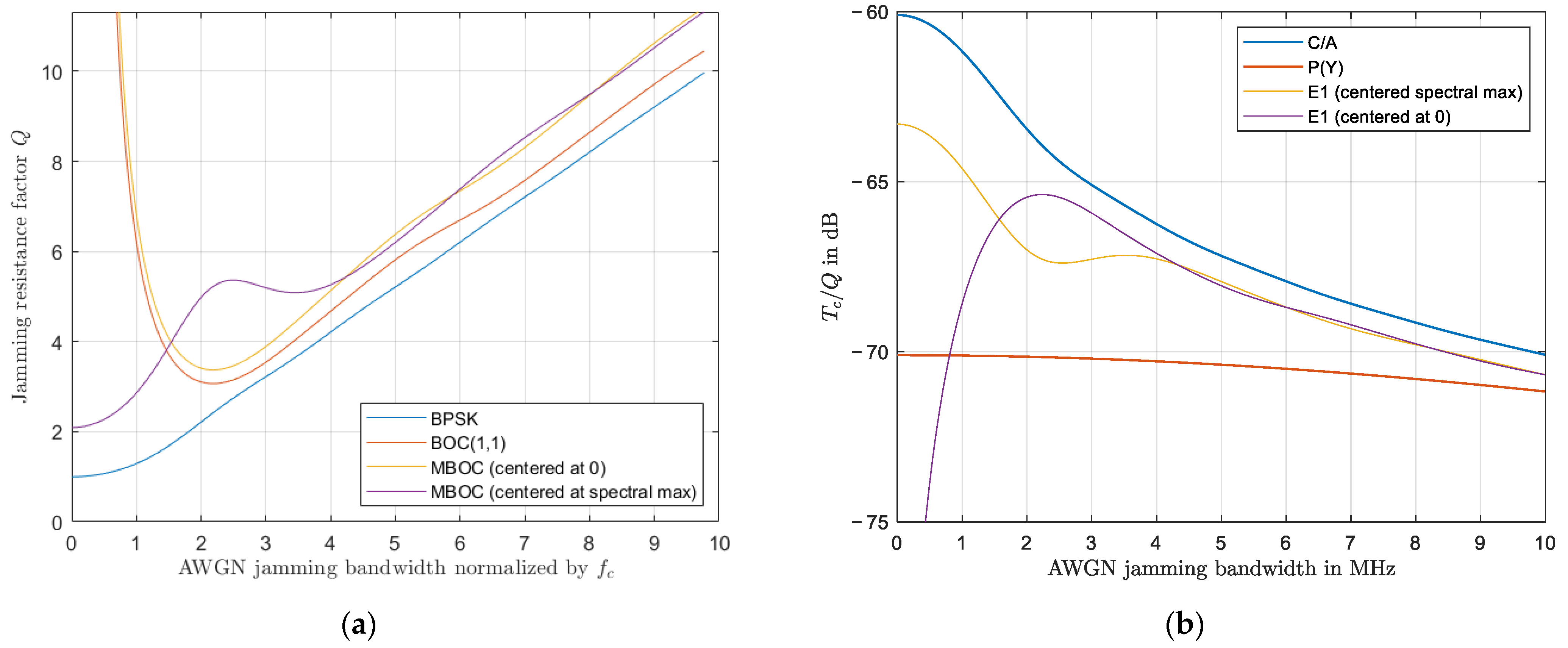In Figure 1a, the value of $Q$ is given for different GNSS signal modulations and a white noise interference source as a function of the normalized (by the chiprate $f_s)$ bandwidth of the interference. From this figure, it is clear that the $Q$ for the CBOC modulation is always higher than the $Q$ for the BPSK signals. Note, however, that $Q$ in this figure is independent of $T_c$, so the fact that $Q$ is always higher does not indicate that all CBOC GNSS signals are less affected by jamming than BPSK signals, as the $T_c$ might be different. This is clearly visible in Figure 1b, where the $T_c/Q$, as it appears in (3), is given for the GPS C/A, GPS P(Y), and Galileo E1-OS signals versus the bandwidth of an AWGN jammer. In this figure, a higher $T_c/Q$ indicates a greater impact of the jammer.

Clearly, the C/A code is most affected by the jammer, while the P(Y) code, although a BPSK signal, performs best because of the 10-times higher chip rate (smaller $T_c$).

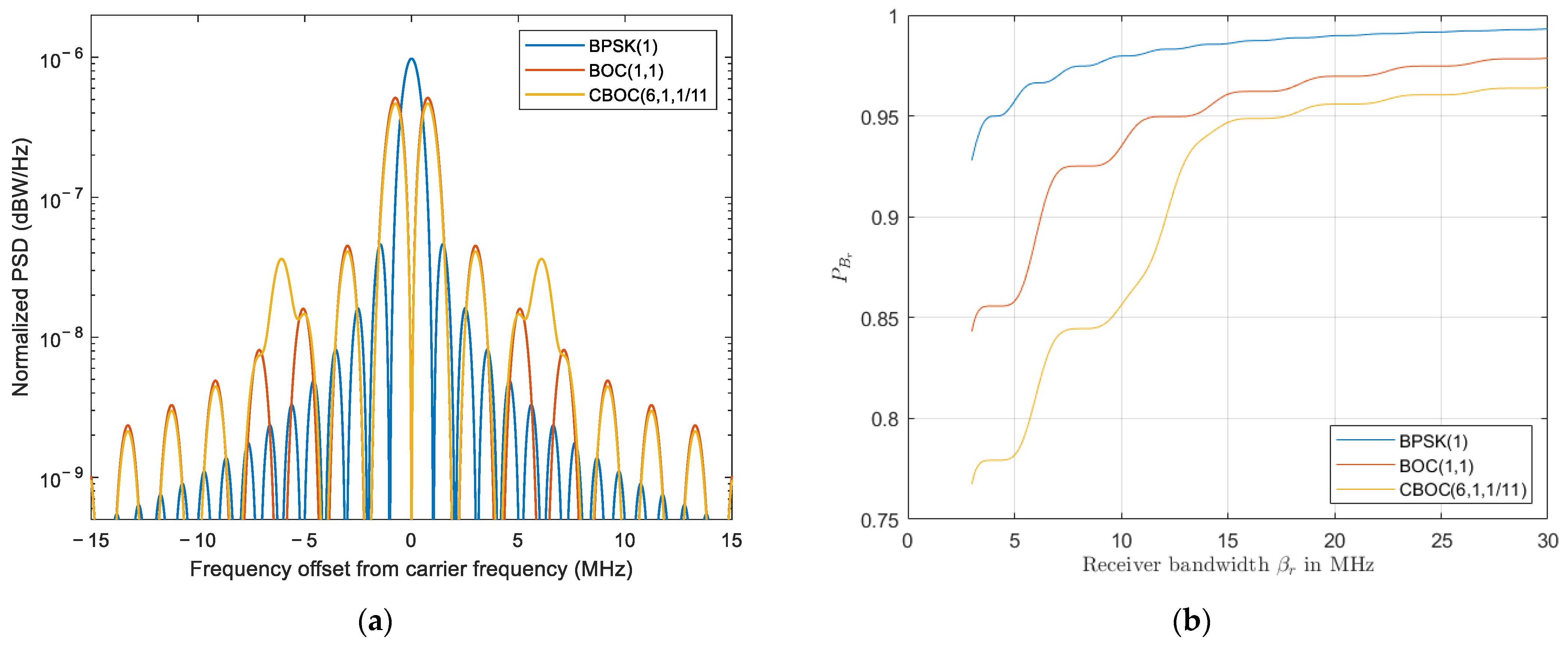
Upon observing Figure 1a, it also becomes clear that the CBOC modulation performs differently compared to the binary offset carrier (BOC) modulation, despite the fact that the spectra of both signals are quite similar (see Figure 2a). The difference in performance can be explained by the slight difference in the distribution of the power over the spectrum. The power of the CBOC modulation is spread out over a larger bandwidth, which is visible by the additional power at a frequency offset of around 6 MHz. As long as the power of the received signal within the bandwidth of the jammer is smaller for the CBOC signal, the signal will be less affected by the interference. The difference in bandwidth is also visible in Figure 2b, where the normalized received power of the signal is given as a function of the receiver’s front end bandwidth. At a bandwidth of 10 MHz, the received power of a CBOC signal is slightly over 85%, while the received power of a BOC(1, 1) signal is around 93%. Even at a bandwidth of over 30 MHz, the difference is still around 1.5%.

Finally, when looking at Figure 1a, it is notable that the impact of a jammer is maximized by minimizing the bandwidth of the jammer while transmitting at the frequency of the spectral maximum of the target signal. Further, for the (C)BOC signals, the impact of a jammer at the central frequency with a relatively small bandwidth (<0.5 MHz) is, in comparison to the other signals, small. This can be explained by the absence of signal power around the central frequency (see Figure 1a). If the same jammer is transmitting at the frequency of the spectral maximum, the impact is greater, though not as great as for the BPSK signals. Most jammers, however, do not transmit at a narrow bandwidth, as this may be filtered out by, for example, a notch filter.

Once the impact of the jammer on the $C/N_0$ is known, the impact on the accuracy of the DLL can be calculated using (1) and/or ($2$).

3. GNSS Jamming Experiment

The equations provided in the previous Section were compared to actual measurements. These measurements were obtained with a software-defined receiver. As over-the-air jamming in the GNSS frequency bands is strictly prohibited, a high-fidelity GNSS receiver was used to generate the satellite signals along with a GNSS jammer signal.

3.1. GNSS Simulator

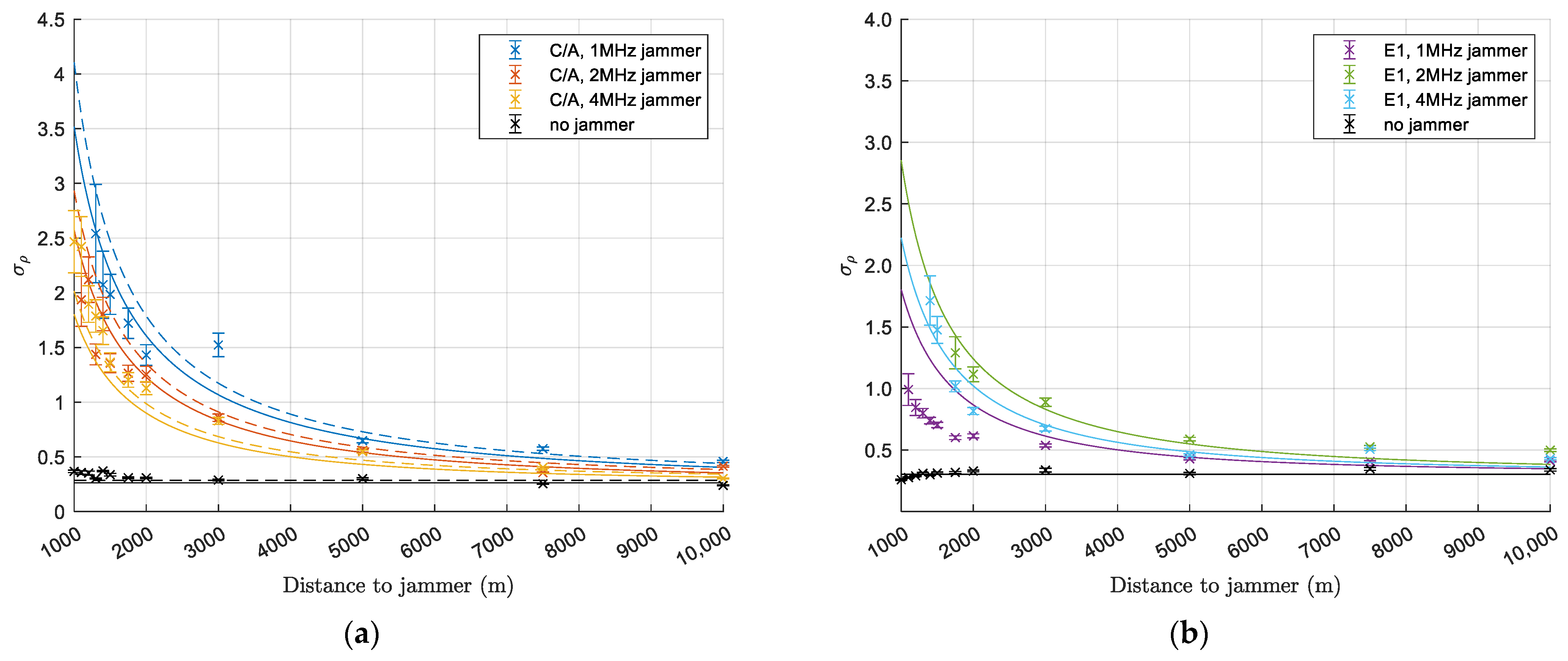
The GNSS simulator used in the experiments was the Orolia Broadsim, which runs the Skydel simulator software. This simulator replicates the GNSS signals, in our case, GPS C/A and Galileo E1, at a chosen position and time. The simulator allows one to place a jammer with user-defined characteristics, like the signal modulation, bandwidth, center frequency, etc., at a certain fixed location or on a moving trajectory. In the experiment, the jammer was set as an AWGN jammer with a transmission power of 20 mW and with different bandwidths of 1, 2, and 4 MHz. The distance from jammer to receiver was varied between 1000 m and 10 km. All simulated experiments were performed 30 m above a flat terrain, with no obstructions of any kind present. The receiver antenna was set to be isotropic in the simulation.

3.2. Software-Defined GNSS Receiver

The receiver used in the experiments was the open-source software-defined GNSS receiver GNSS-SDR [4]. A software-defined receiver was chosen because it allows one to exactly define the tracking parameters that do influence the accuracy of the receiver. With commercially available receivers, the user usually has no control over these parameters, which complicates the theoretical prediction of their accuracy. The signals were captured using a USRP B210 front end, which was directly connected to the simulator output using a coax cable, so no signals were transmitted over the air. The signals were captured at a sample frequency of 16 MHz as 16-bit IQ data at a central frequency of 1575.42 MHz.

For GPS C/A code tracking, an early-minus-late discriminator was used, with an early-late spacing of 0.4 chips, a DLL loop bandwidth of 0.25 Hz, and an integration time of 10 ms. For Galileo E1 tracking, the GNSS-SDR very-early-minus-very-late discriminator was used, with an early-late spacing of 0.2 chips. The very-early-late spacing was set to be equal to the early–late spacing such that the very-early-minus-very-late discriminator effectively became an early-minus-late discriminator. This setup might result in ambiguity problems due to the additional correlation peaks of the CBOC modulation. This problem, however, was not observed in these experiments. The loop bandwidth for E1 was set to 0.25 Hz, and the integration time was set to 8 ms. The output of the receiver was configured as RINEX files, which contain the pseudo-range, carrier phase, and $C/N_0$ measurements of the tracked satellites, with a rate of 10 measurements per second.

3.3. Experimental Setup

The experiments were performed in the following way: The first 1.5 min were measured without the jammer being active to allow the receiver to obtain a fix, usually within 25 s, and establish a baseline for performance without jamming. After 1.5 min, the jammer was turned on, and after 3 min, measurement ceased. This process was repeated for distances between the jammer and receiver from 1000 m up to 10 km and for the different jammer bandwidths of 1, 2, and 4 MHz.

The duration of the captured signals was limited by the hardware used to log the USRP-B210 output. Due to the hardware limitations, the maximum file size of the log files was 12 Gb, which led to a maximum duration of only 3 min.

4. Comparison of Theoretical and Measured Results

In this Section, the results of the comparison of the theory versus the measurements are provided. First, the measured impact of the jammer on the $C/N_0$ is compared to the predicted impact based on Equation (3). Next, the impact on the DLL tracking accuracy is compared to the measured standard deviations of the detrended pseudo-range measurements.

4.1. Carrier-to-Noise Ratio

In Figure 3, the measured versus theoretically expected decreases in the $C/N_0$ and $\mathsf{\Delta }C/N_0$ are shown for a jammer with 1, 2, and 4 MHz bandwidths. The solid line is the expected $\mathsf{\Delta }C/N_0$ based on the theory, the cross is the average of the measured $\mathsf{\Delta }C/N_0$, and the error bar indicates the standard deviation of the measurements. The more negative the $\mathsf{\Delta }C/N_0$, the greater the impact of the jammer on the $C/N_0$. The measured average $\mathsf{\Delta }C/N_0$ was determined by subtracting the average of the $C/N_0$ measurements taken in the last minute (approx. 600 samples) by the average of the measurements taken in the last minute before the jammer was turned on.

The $C/N_0$ measurements confirm the theoretical results exceptionally well for both GPS C/A (Figure 3a) and Galileo E1 (Figure 3b). As expected, as shown in Figure 1, the impact of the jammer on the $C/N_0$ of GPS C/A increases with a decreasing jammer bandwidth. For Galileo E1, the effect is different. The impact of the 1 MHz and 4 MHz jammers is less than the impact of the 2 MHz jammer. This was expected based on Figure 1, as the $Q$ at 2 MHz is close to the theoretical minimum at a bandwidth of approximately 2.2 MHz. Also, as expected, the Galileo E1 signals are less affected by the jammer than the GPS C/A signals.

From these results, we can conclude that the impact of a jammer on the $C/N_0$ can be accurately predicted using (3) for both GPS C/A and Galileo E1 signals.

4.2. Accuracy of the Pseudo-Range Measurements

In Figure 4, the standard deviations of the pseudo-range measurements are given for GPS C/A (in Figure 4a) and Galileo E1 (in Figure 4b). These standard deviations provide a measure of the accuracy of the DLL and, with it, the pseudo-range for unbiased measurements. The solid lines indicate the predicted standard deviations calculated using (1). In Figure 4a, the standard deviations as predicted using (2) are also given (as dashed lines). These standard deviations of the measurements were determined after detrending the pseudo-range measurements using a third-order polynomial in order to remove the effect of satellite motion. The standard deviations of the measurements with the jammer active were determined in the last minute of measurements. The standard deviation of the measurements without the jammer was determined in the last minute of measurements before the jammer was turned on. Both figures show the results regarding the signals of a single satellite.

For GPS C/A (Figure 4a), the predictions match the measurements reasonably well with and without the interference of the jammer. Although both models, given by (1) and (2), provide slightly different values, both predict the accuracy well. Again, it is clear that the jammer with the narrowest bandwidth has the largest impact and that the largest jammer bandwidth has the lowest impact, as expected for a BPSK signal (see Figure 1).

For Galileo E1 (Figure 4b), the predictions for the situation without the jammer and with the 2 MHz and 4 MHz jammers do match the measurements; however, the predictions for the 1 MHz jammer overestimate the standard deviations found based on the measurements when the jammer is relatively close. Further away from the jammer, the estimations match the measurements well. This overestimation close to the jammer was persistent for all the satellites analyzed, of which only one is given in the figure. Both the predictions and the measurements show that the 1 MHz jammer has the least impact, while the 2 MHz jammer has the largest impact, exactly as expected for CBOC signals (see Figure 1).

Upon observing Figure 4, it becomes clear that the pseudo-range accuracy significantly deteriorates when closer to the jammer. If, for example, the required accuracy is twice the expected nominal accuracy, the effective range of this 20 mW jammer on a GPS C/A receiver is around 3500 m for the 4 MHz jammer to 7000 m for the 1 MHz jammer. For a Galileo E1 receiver, this range is between 3000 m for the 1 MHz jammer and 4500 m for the 2 MHz jammer. This range is significantly larger than the range in which the receiver will lose its lock on the signal; this range is between approximately 1000 and 1500 m for the receiver used, depending on the bandwidth of the jammer.

5. Conclusions

In this paper, the effect of an AWGN jammer on the pseudo-range accuracy of a GNSS receiver was investigated. First, the theoretical background was provided, after which the theory was compared to actual measurements. The major impact of a jammer on a GNSS receiver is a reduction in the $C/N_0$. The model provided to predict the impact on the $C/N_0$ showed a close match with the actual measured impact. From this, it can be concluded that Equation (3) predicts the suppression of the $C/N_0$ by a AWGN jammer very well. Next, the prediction of the standard deviation of the pseudo-range tracking error, given by Equation (1), was compared to the standard deviations of the measured pseudo-range. For GPS C/A, the prediction matches the observation reasonably well. For Galileo E1, the predictions show some differences, but the general trend and order of magnitude are similar. This shows that the standard deviation of the pseudo-range measurements can also be predicted, although not as accurately as the $C/N_0$. From this, we can conclude that the theory can be used to predict the performance of a GNSS receiver under jamming. This will allow us to determine the effective range of a jammer, in this case, an AWGN jammer, for applications where the accuracy of the position solution has certain requirements. This effective range is likely to be much larger than the range at which the receiver loses its lock on the signals.