Investigation of Static and Kinematic Surveying Performance of Handheld GNSS Receiver ^†

Abstract

In this study, the static and kinematic positioning performance of the Garmin GPSMAP 66sr handheld GNSS receiver has been tested. For the static test, GNSS data was collected for 24 h and divided into shorter sessions of 1, 2, and 4 h to assess the performance of the receiver as a function of occupation time. The whole and subgroup data were processed by the relative method for different satellite constellations using three reference stations, to form a very short (45 m), short (5.1 km), and relatively long (73.2 km) baselines. For the kinematic test, the data was collected for approximately 1 h and processed with the relative method. Additionally, the whole and subgroup static and kinematic GNSS data of the Garmin receiver were also processed with the Canadian Spatial Reference System-Precise Point Positioning (CSRS-PPP) online service. All Garmin static and kinematic solutions (both relative and PPP) were compared with those calculated by the geodetic receiver. The overall static results show that the Garmin GPSMAP 66sr handheld receiver provides accuracy in a few centimeters with the relative method when integer ambiguities were correctly fixed and in the decimeter-to-meter level using the PPP technique. For the kinematic scenario, the results were relatively poor within the level of decimeters with the relative method while the level of meters with the PPP technique.

1. Introduction

The Global Navigation Satellite Systems (GNSS) has become a widely used standard positioning tool today. It is possible to achieve different levels of accuracy depending on the method applied in satellite-based positioning systems. For example, for low accuracy requirements at the meter level, standard navigation-type receivers that can determine absolute position using code measurements are sufficient, while for centimeter-millimeter accuracy requirements, the relative method using carrier-phase measurements must be applied.

Today, the Precise Point Positioning (PPP) technique, which does not require additional reference station observation but can produce the accuracy provided by the relative method, has found use in many applications [1,2,3,4]. This technique, which combines raw data collected with a single GNSS receiver and precise satellite clock & orbit corrections, enables 3D positioning with an accuracy of a centimeter-millimeter level, depending on occupation time, used receiver and equipment, number of frequencies (single or multi-frequency), tracked satellite constellations and environmental survey conditions (multipath, etc.). However, to achieve this accuracy, a long convergence time of 15–30 min is needed [5]. This issue limits the use of the method in real-time applications. Recently, an ambiguity-fixed solution has been obtained by using satellite phase bias values during the PPP solution. With this approach, called Precise Point Positioning-Ambiguity Resolution (PPP-AR), accuracy has increased and convergence time has also been shortened [6,7]. In order to obtain a high-accuracy position with both the relative method and the PPP technique, code and phase measurements collected with geodetic-type receivers should be used. This also means using at least 2 geodetic receivers for the relative method and at least 1 for PPP. Although the prices of these receivers vary depending on manufacturer policies, they can reach quite high values (up to 20K USD or even more each).

On the other hand, as a result of the developments in hardware and informatics technologies, raw GNSS measurements (code, Doppler, carrier-phase observations, and others) can now be collected with smartphones and tablet computers. These types of devices have attracted the attention of the academic community, and the positioning performances of smartphones and tablet computers have been investigated in many academic studies [8,9,10,11]. These studies demonstrated that better accuracy can be achieved, especially when carrier phase data is collected with geodetic-type antennas. On the other hand, there are some limited studies on the usability of handheld GNSS receivers for high-accuracy positioning [12,13,14]. However, when these studies were investigated, it was seen that the collected raw data was not provided by the manufacturer with standard protocols, and it is not commercially available. Thus, the researchers collected the data with their in-house software. This situation has also restricted the widespread use of such devices in geodetic applications. In 2018, Garmin Ltd. provided the raw GNSS data commercially with the Garmin handheld receiver, which is mainly used for navigation, outdoor, marine, and sports activities, and this paved the way for using such devices in high-accuracy positioning. There are few studies conducted with this device in the literature. In one of these studies carried out by Lachapelle et al. [15], the raw data was collected using an external antenna in static and kinematic modes with both GPSMAP 66 handheld and a smartphone with an Android operating system. In the study, it was observed that differential positioning accuracy better than 1 m RMSE could be achieved with a handheld GNSS receiver in vehicular mode. In another study carried out by Wanninger et al. [16], the performance of the Garmin GPSMAP 66sr handheld GNSS device was investigated, and it was revealed that it provided positioning with centimeter accuracy in dual-frequency GPS&Galileo PPP static mode. In the study conducted by Alkan et al. [17], the static measurement performance of the Garmin GPSMAP 66sr unit was investigated, and they found that the accuracy could be achieved at the cm level with the relative method and at the meter-to-decimeter level with the PPP technique.

In this study, the usability and performance of a handheld GNSS receiver, which costs a few hundred dollars (~500–700 USD), was investigated in geodetic measurements.

2. Materials & Methods

2.1. Static Field Measurement

Static GNSS measurements were made for 24 h at a control point (CP-1) established on the roof of the Civil Engineering Faculty in Istanbul Technical University (ITU) Campus, Istanbul, Türkiye, between 08:45 on 18 September 2023 (GPS Day: 261) and 08:45 on 19 September 2023 (GPS Day: 262). In the measurements, the Garmin GPSMAP 66sr handheld receiver was used (Figure 1a,b). It was introduced in 2020 as the first dual-frequency multi-constellation handheld GNSS receiver. The receiver has a quad helix antenna, which plays a vital role in reducing the multipath effect by creating a circularly polarized hemispherical radiation pattern [16]. It has a BCM47758 chipset and can track the L1 and L5 GPS (G) signals; L1 GLONASS (R) signals; E1 and E5a Galileo (E) signals. It is also capable of tracking QZSS and IRNSS signals [18]. During static measurements, GNSS raw data was recorded in RINEX v.3.04 format at a 1-s measurement interval from all available GPS, GLONASS, and Galileo satellites. There is an issue that is worth emphasizing here since only GPS and GLONASS observations were collected at the reference stations used in the relative solution, only GPS (L1 and L5) and GLONASS (L1) satellite observations were used during the process in the static scenario. The tracked GNSS number of satellites and Position Dilution of Precision (PDOP) values are given in Figure 1c,d. Site-dependent multipath is one of the sources of GNSS errors that affect both code and carrier-phase measurements. Studies have revealed that there is a strong correlation between multipath and Signal-to-Noise Ratio (SNR) [19]. Therefore, multipath also affects the SNR of the measurements. In this context, SNR on L1 and L5 signal values, which express the quality of GNSS signals, were calculated and plotted in Figure 1e as a skyplot. In addition, multipath values affecting the measurements were also calculated and presented in Figure 1f as a skyplot. The SNR and multipath plots were generated using RTKLIB and in-house software.

2.2. Kinematic Field Measurement

In order to assess the kinematic performance of the Garmin handheld GNSS receiver, a kinematic measurement campaign was carried out in the stadium located on the ITU Campus on 29 July 2023 (GPS Day of Year: 210). At the beginning of the measurements, data was collected for approximately 30 min without movement (as static), and then measurements were continued by walking in the stadium for about 30 min. In order to get the kinematic performance of the Garmin receiver, simultaneous measurements were carried out with a geodetic-grade GNSS receiver (to obtain known coordinates of each measured epoch for use in comparison) that is connected to the same measurement pole as the Garmin receiver (Figure 2a,b). In this way, GNSS data was collected by the Garmin GPSMAP 66sr and geodetic-grade receivers under almost the same conditions, which allows for precise assessment of the Garmin receiver. In the kinematic campaign, GPS, GLONASS, and Galileo observations were collected at a 5-s sampling rate, and the GNSS raw data was logged in RINEX format into the receiver’s internal memory. The tracked number of GNSS satellites and Position Dilution of Precision (PDOP) values for the kinematic measurement campaign were given in Figure 2c,d. Signal-to-noise ratio (SNR) and site-dependent multipath plots were created with RTKLIB v.2.4.3-b34 Manual and in-house software and were given in Figure 2e,f.

3. Performance Analysis Results and Discussions

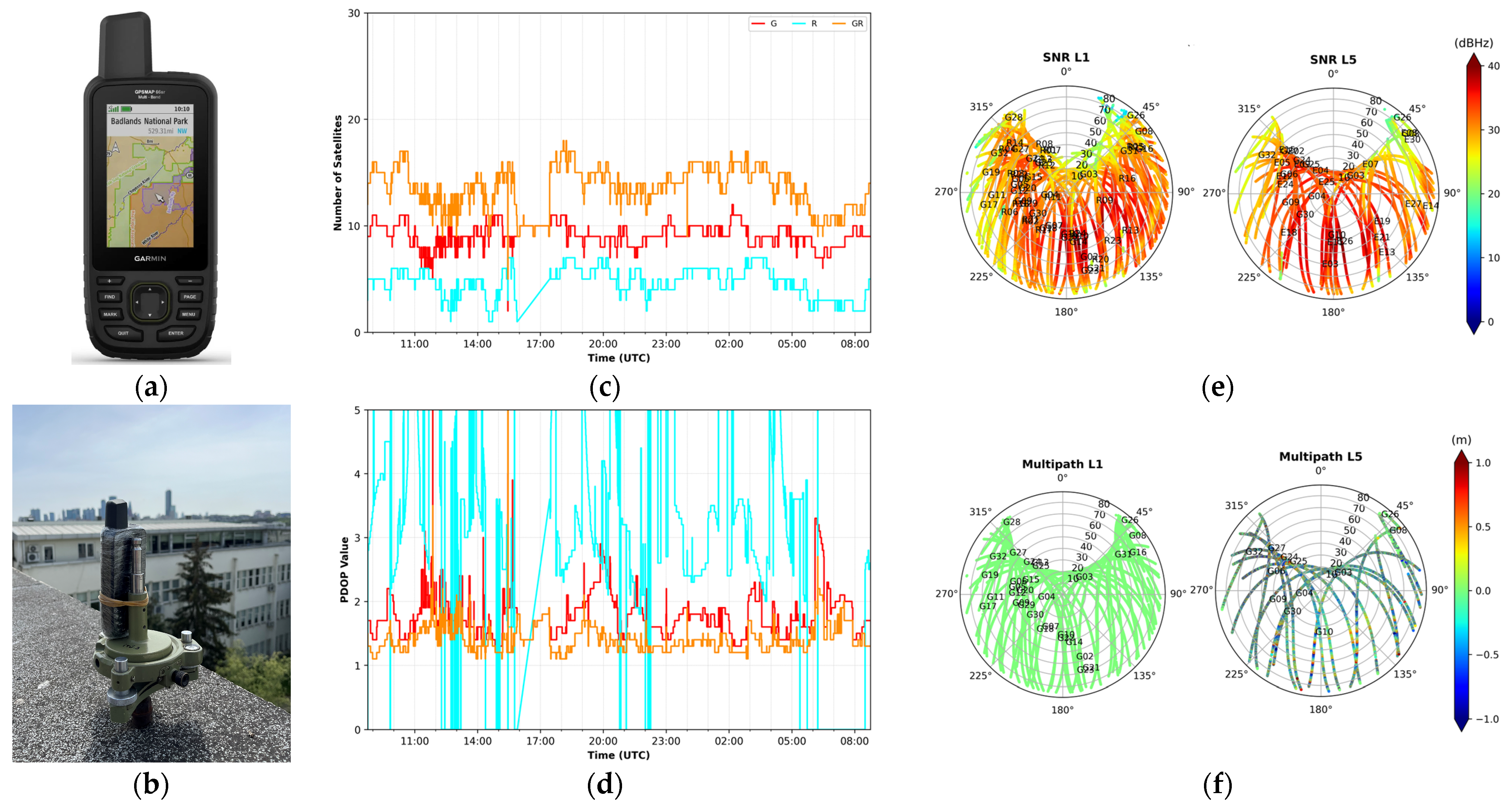
3.1. Static Scenario

Static data collected with the Garmin receiver was first processed using the relative positioning method. During the process, three GNSS reference stations located at different distances from the Garmin receiver were used to reveal the effect of baseline length on static positioning accuracy. One of the International GNSS Service (IGS) stations, ISTA, and two of the continuously operating reference stations, PALA and YALI, were used as reference control stations to form a very short, short and relatively long baselines of about 45 m, 5.1 km, and 73.2 km, respectively. In addition, the collected daily dataset was also divided into shorter sessions of 1, 2, and 4 h to assess the performance of the receiver as a function of occupation time. All these formed baselines were processed with Topcon MAGNET Tools GNSS software v.8.1 using IGS precise orbit files. Tropospheric path delay was modeled using the VMF3 grid product. In order to investigate the effect of the satellite constellation on the accuracy performance, all baselines were processed with two different satellite constellations as GPS (G-only) and GPS&GLONASS (G&R) combination. The observations on the L1 and L5 frequencies for GPS and L1 frequency for GLONASS constellations were used. The coordinates of the handheld receiver were estimated both as fixed or float ambiguity resolutions depending on the baseline length and occupation time.

The coordinates of the Garmin receiver obtained with baseline solutions were compared with the known coordinates of the point (CP-1), and the differences in 2D position and ellipsoidal height components for all solutions were given in Figure 3a,b. It should be noted that the differences in the order of meters were obtained in ambiguity float solutions; thus, only the results of ambiguity-fixed solutions were given here. The term “Float Sol.” in the graphics means that the corresponding solutions were obtained as “ambiguity-float solution”. The others indicated that the coordinates were estimated with ambiguity-fixed solution.

The same datasets were also processed with the Canadian Spatial Reference System-Precise Point Positioning (CSRS-PPP), one of the most widely used online GNSS PPP processing services. The service was launched in 2003 and estimates the accurate coordinates in PPP mode using precise satellite orbits, clock corrections, and biases. In this service, PPP coordinates are derived using the L1 and L2 frequencies of the GPS and GLONASS constellations. It is sufficient for users to send the GNSS data collected in the field in RINEX, *.zip, *.gz, *.z, *.tar, *.yyo formats via the user-friendly website of the service. CSRS-PPP produces ITRF solutions in the IGS20 reference frame, starting with GNSS measurements logged on Sunday, 27 November 2022. The most recent information on this service can be found in Banville et al. [20] and the CSRS-PPP website (https://webapp.geod.nrcan.gc.ca, accessed on 20 May 2024). Shortly after sending the data to the service, combined GPS&GLONASS PPP-derived coordinates, including many outputs containing different information, graphics, and detailed solution reports, were sent to the e-mail address that we introduced at the beginning.

The static PPP coordinates of the Garmin receiver were compared with the known coordinates, and the differences were given in Figure 4 as 2D position and height for the G&R combined solution at different occupation times. It should be noted that although the Garmin receiver dataset contains L1 and L5 frequencies, only the L1 frequency is used in the solution. Accordingly, the PPP coordinates are calculated with a single-frequency solution. The reason for this is that the CSRS-PPP service uses only L1 and L2 frequencies, while it does not use L5 data.

As a result of all these findings for static trial, the following concluding remarks could be stated:

• It was seen from Figure 1c that the number of visible satellites varied between 2 and 12 for GPS (9 on average) and between 1 and 7 (5 on average) for GLONASS. In the combination of GPS and GLONASS, the maximum number of satellites reached to 18, and the average number of satellites increased by 55% when compared to G-only and 180% compared to R-only solutions, reaching 14. As seen here, multi-constellation systems significantly increased the number of satellite observations compared to single systems.
• When examining the PDOP values given in Figure 1d, it was seen that the G-only PDOP value reached a maximum of 7 (with an average of 2), and there were large fluctuations in the R-only PDOP values. Additionally, the G&R combination did not provide a significant contribution to PDOP values compared to GPS-only solutions.
• It is seen that from Figure 1e, the majority of SNR values were above 35 dBHz, which was accepted as the limit value [21]. When we looked at the code multipath values, it was seen that the L1 multipath values were in the order of 1–2 dm, whereas the L5 signals had high values, up to the meter level.
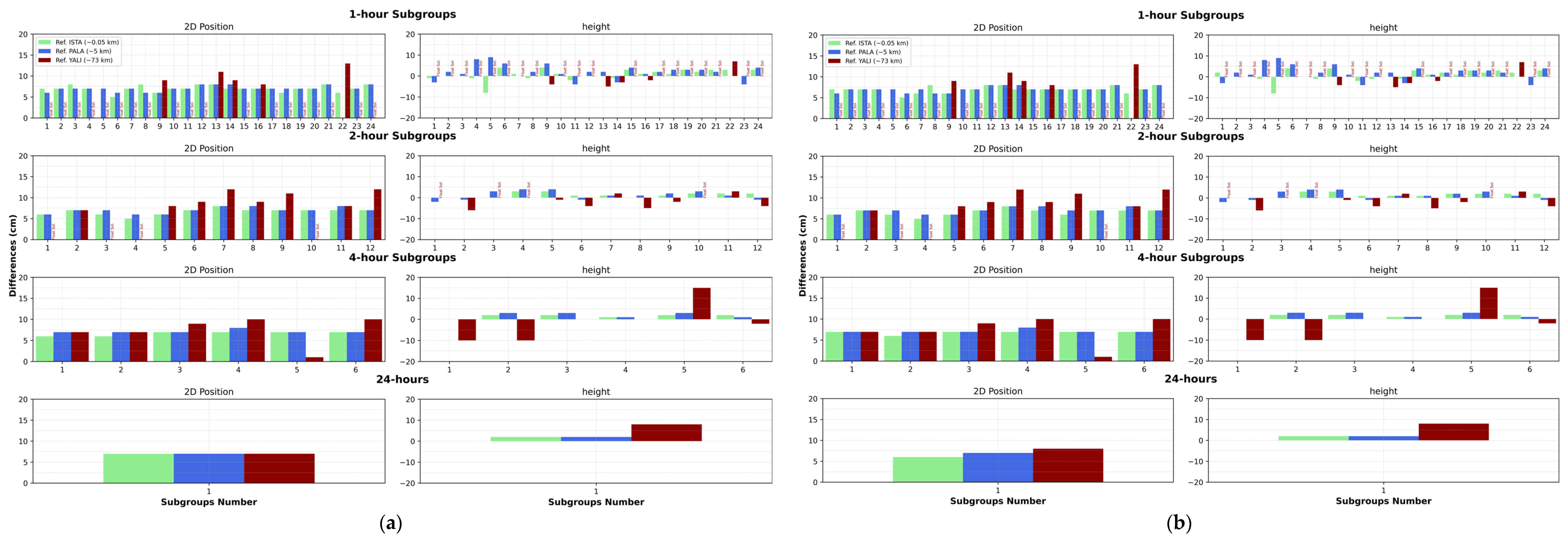
• According to Figure 3, for both G-only and G&R combinations, ambiguity-fixed solutions could be obtained in relative solutions with all occupation times of 2 h and more for a 5.1 km baseline length. This situation was similar for 1-h occupation times, with a few exceptions. The results for the 73.2 km baseline length were relatively poor, especially when the 1, 2, and 4-h sessions were used. For the 73.2 km long baseline length, a minimum of 4 h of measurement was required for the ambiguity-fixed solution. In general, it was observed that 1–2 h of occupation time can provide an ambiguity-fixed centimeter-level solution for short baselines. For a long-baseline solution, it should be made the observations at least 4 h or more occupation time for an ambiguity fixed solution. Furthermore, the G-only solutions results were found comparable to those obtained with the G&R combined solutions.
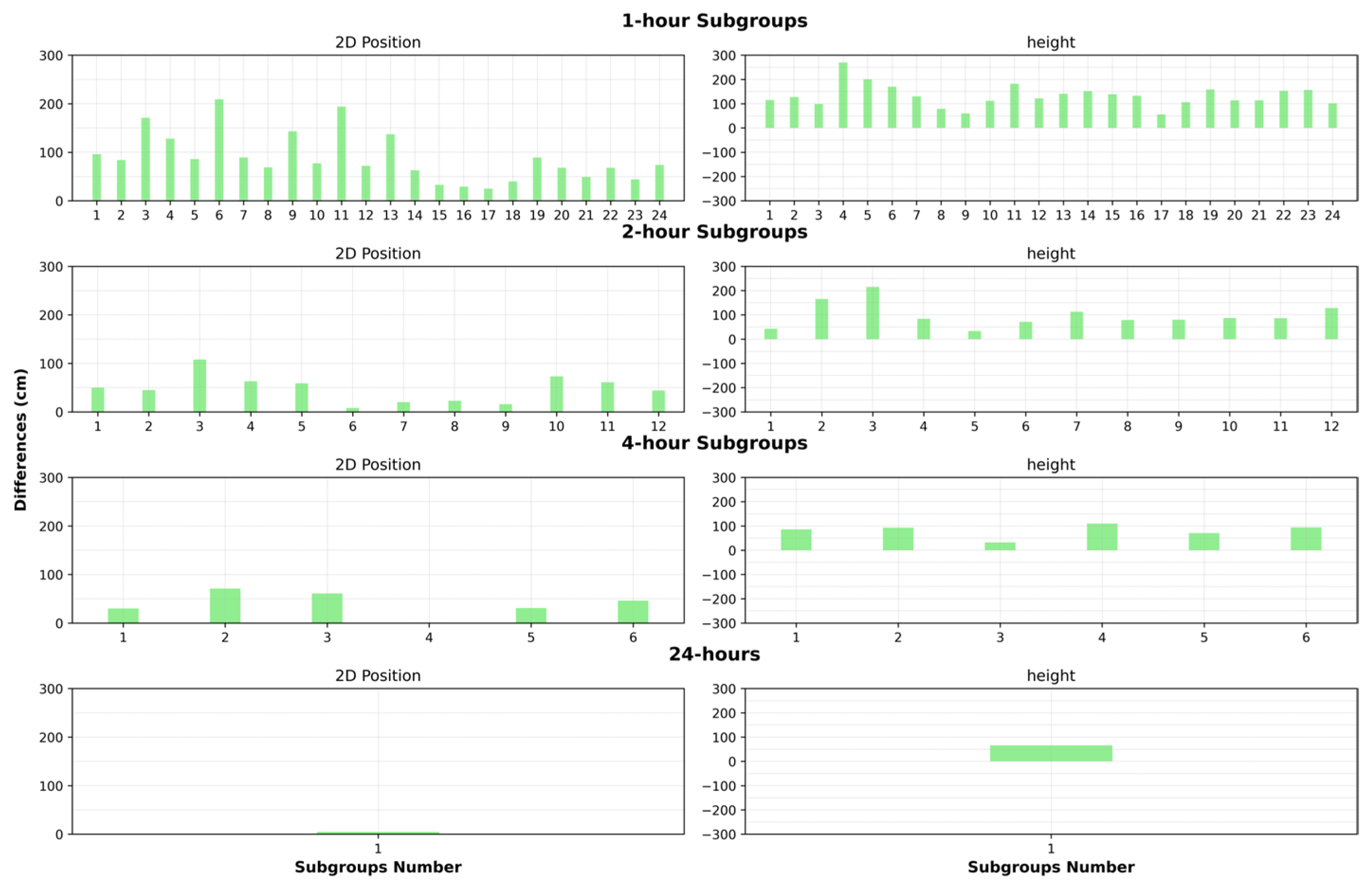
• When the static PPP solution results given in Figure 4 were investigated, it was seen that 24-h occupation time was required to achieve 2D position accuracy at the cm-level. For other subgroups (1, 2, and 4-h sessions), differences in the order of meters-to-decimeter level were obtained. The most probable reason for such poor results in the PPP solution was that although the Garmin receiver collects GPS L1&L5 and GLONASS L1 signals, the CSRS-PPP service does not use the L5 signal and provides a solution using the L1 frequency only (i.e., single frequency solutions).

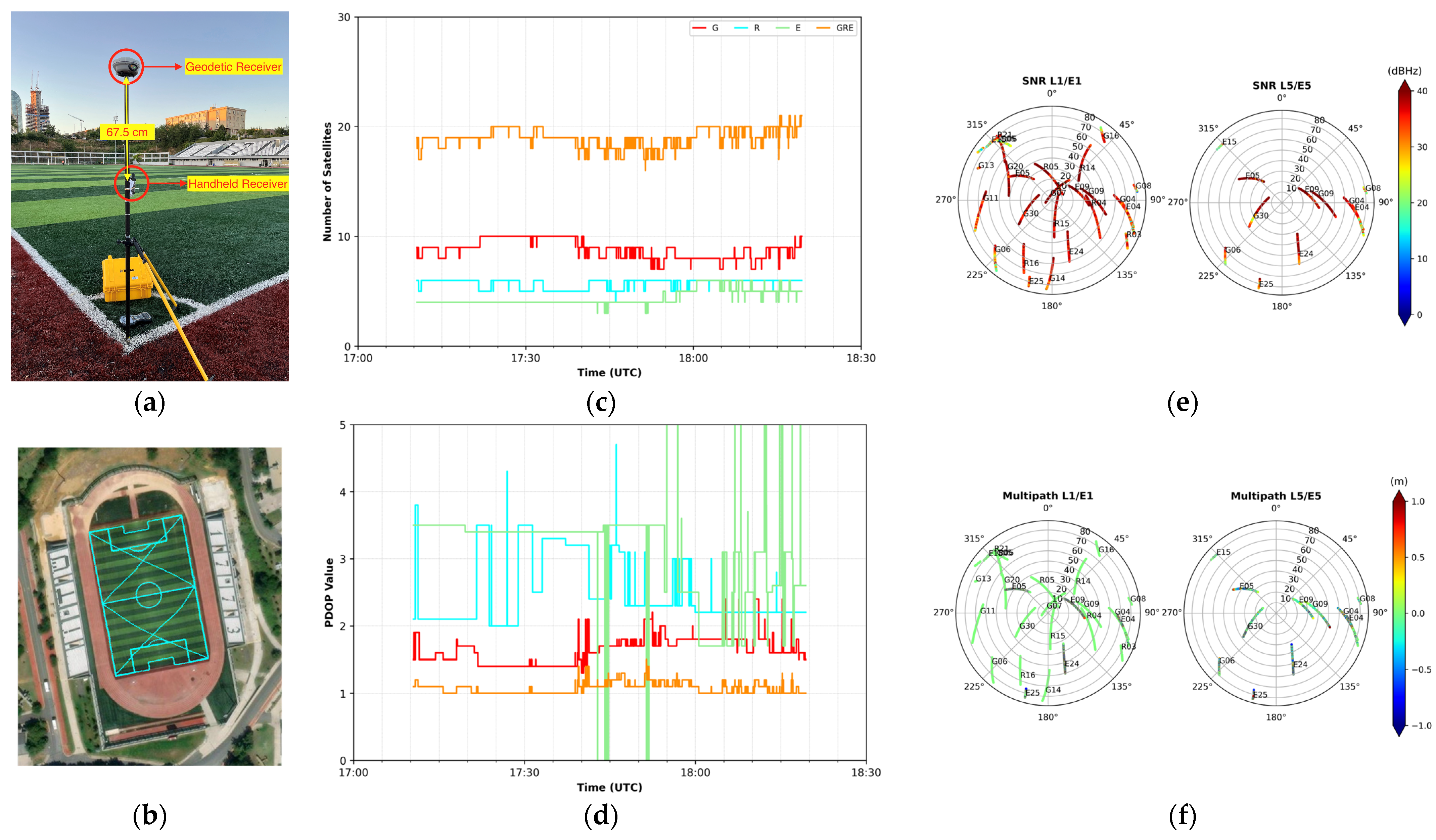
3.2. Kinematic Scenario

The collected Garmin kinematic data was first processed with the relative method. The ISTA IGS reference station, a few hundred meters away, was used as the reference station. The coordinates of each measurement epoch were calculated as an ambiguity-fixed solution using carrier phase data with Topcon MAGNET Tools GNSS software. It should be noted that the coordinates were calculated under two different satellite configurations, i.e., G-only and G&R&E combination. The observations on the L1&L5 frequencies for GPS, L1 frequency for GLONASS, and E1&E5 for Galileo constellations were used. In order to assess the attainable accuracy with the Garmin receiver, the reference trajectory should be established. In this frame, the known coordinates were calculated by processing the kinematic data collected with the geodetic receiver that was attached to the same measurement pole using the relative method. The baseline length varied from 400 to 520 m between the rover and the ISTA reference station. The differences in 2D position and height components between the Garmin receiver and known coordinates are given in Figure 5a,b as a time series.

The kinematic dataset was also processed with the CSRS-PPP online service in kinematic mode. As mentioned before, the CSRS-PPP service produces single-frequency solutions for Garmin receiver. The PPP coordinates calculated by the service were compared with known coordinates, and the differences are plotted in Figure 5c.

The result of all these findings for the kinematic test is given in Figure 2 and Figure 5, the following concluding remarks could be stated:

• When Figure 2c was examined, it was seen that the number of satellites varied between 7 and 10 for GPS (9 on average), 4 to 6 for GLONASS (6 on average), and also 3 and 6 for Galileo (4 on average). With the combination of GPS, GLONASS, and Galileo, the maximum number of satellites increased to 21, and the average number of satellites significantly increased to 14 compared to the single system. As seen here, multi-constellation observations significantly increased the number of satellites compared to single-system observations.
• When looking at the PDOP values (Figure 2d), it was seen that the maximum PDOP value reached 2, 5, and 8 for GPS, GLONASS, and Galileo satellites, respectively. Unlike static measurements, it was seen that GLONASS satellites had better PDOP values in kinematic measurements. It was also observed that there were fluctuations in Galileo PDOP values. In triple-configuration, an average PDOP value of around 1 was reached, with significant improvements compared to single systems.
• When Figure 2e,f were examined, it was seen that the majority of SNR values were above 35 dBHz. When we looked at the multipath values, it was seen that the multipath values were in the order of 1–2 dm for L1/E1 signals. On the other hand, it seemed that the multipath effect was greater for L5/E5 signals.
• Looking at the differences given in Figure 5, it can be seen that there were cm-level differences in both the 2D position (as a maximum of ~8 cm) and the height (as a maximum of ~5 cm) in the initial (static) part of the kinematic measurements for the G-only relative solution. For the kinematic chain (started after the static time period), it was seen that the differences reached to a couple of decimeters in horizontal and height components. However, it has been observed that the solution made with the GRE combination improves the solution’s performance.
• Looking at the kinematic CSRS-PPP results given in Figure 5c, it can be seen that the performance of the kinematic PPP technique is far from meeting the requirements of many geodetic applications.

4. Conclusions

In this study, the usability of the Garmin GPSMAP 66sr handheld receiver in geodetic measurements was tested, and its static and kinematic positioning performances were investigated with the relative method and PPP technique. The results of the relative static positioning method showed that as long as the ambiguities were fixed, 2D positioning and height accuracies at the few centimeter-levels can be achieved with an even shorter occupation time. When looking at the relative positioning results of the kinematic test (walking part), it was seen that a couple of decimeters of accuracy for 2D-position and height components were obtained. It has also been observed that the use of multi-GNSS and multi-frequency data in PPK solutions has a significant and positive effect on accuracy performance.

Static data processing results performed with the PPP technique showed that positioning (2D and height) at the meters-to-decimeter level was possible with the Garmin receiver. Additionally, it has been observed that Kinematic PPP results have too low accuracy to be used in geodetic applications. It should be remembered here that both static and kinematic CSRS-PPP solutions use only L1 frequency.

According to the overall results obtained from the study, it was shown that the Garmin handheld GNSS devices can replace high-cost geodetic-type GNSS receivers in certain areas and can be used in many geodetic measurement applications as low-cost and high-accuracy positioning tools. It was also understood that the promising developments in alternative positioning platforms provided a different perspective on positioning with GNSS.