Evaluation of H-ARAIM Reference Algorithm Performance Using Flight Data †
Abstract
1. Introduction
2. Flight Trials and Data Collection
3. H-ARAIM Operational Performance Analysis
- When a satellite is above an elevation angle of 5 degrees, it will be tracked. It is known, however, that aircraft banking can cause the loss of the lock of low elevation satellites;
- The multipath and ionospheric uncertainty are bounded by the elevation-dependent models specified in [15];
- The cycle slips are assumed rare enough, so that the error bound on the multipath is almost always the one provided by the bound in the carrier-smoothed code;
- Space weather conditions are considered quiet at any latitude of simulated grids excluding possible signal outages due to ionospheric disturbances;
- Baseline GPS and GALILEO constellations of 24 satellites are considered, assuming available ranging signals on both L1/E1 and L5/E5a bands for all the satellites [14].
3.1. Multipath and Ionosphere Errors Experienced During Flight Tests
3.2. Accuracy and Integrity Analysis of the Flight Data
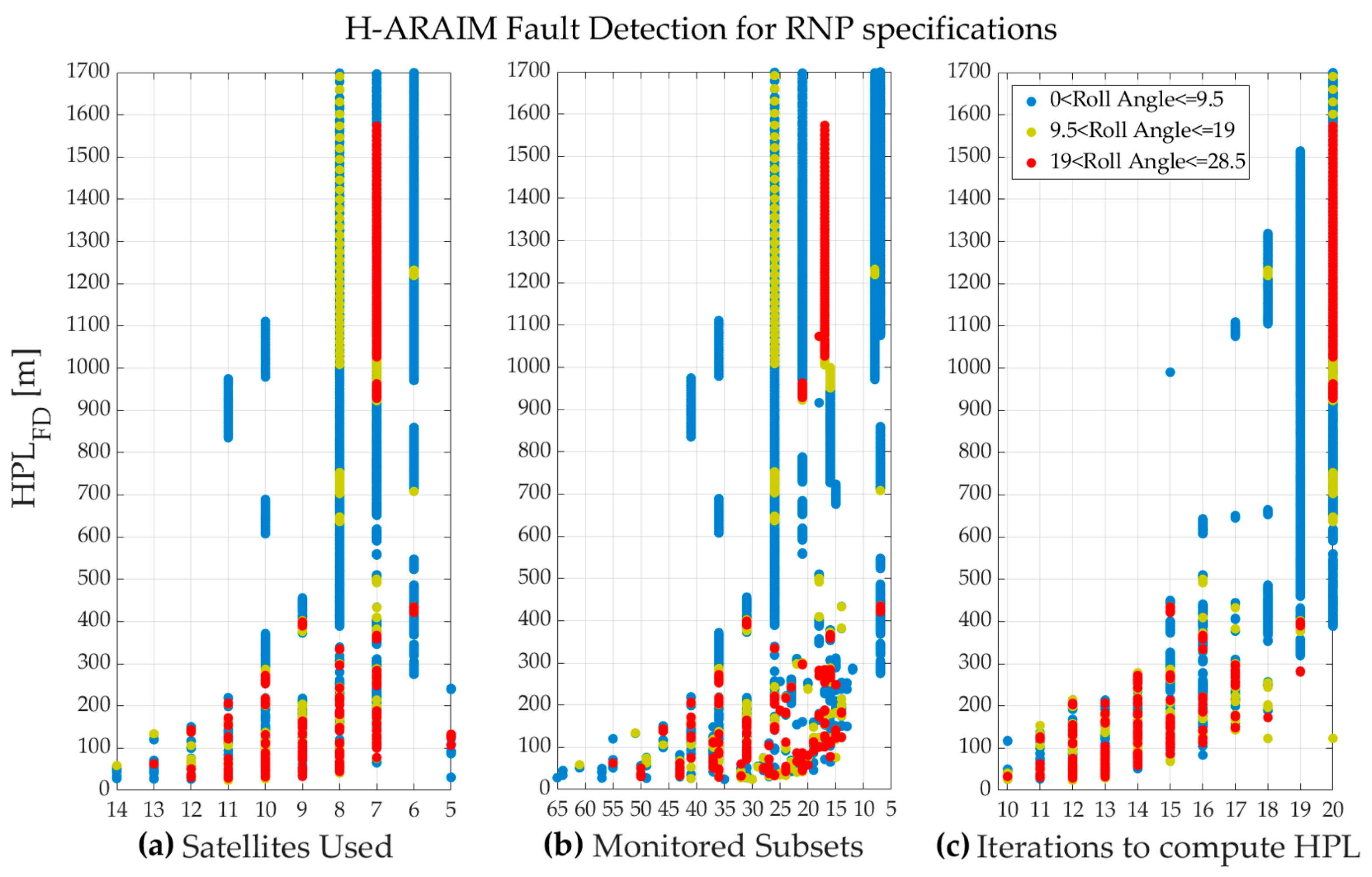
3.3. Analysis of H-ARAIM Sensitivity to Aircraft Dynamics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Working Group-Advanced RAIM Technical Subgroup (WG-C-ARAIM TSG). Advanced RAIM Reference Airborne Algorithm Description Document (ARAIM ADD). Version 4.2. 2023. [Google Scholar]
- She, J.; Misovec, K.; Blanch, J.; Caccioppoli, N.; Duchet, D.; Domínguez, T.E.; Liu, F.; Racelis, D.; Joerger, M.; Sgammini, M. Implementation of the Reference Advanced RAIM User Algorithm. In Proceedings of the ION GNSS+ 2023, Denver, CO, USA, 11–15 September 2023. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Milner, C.; Joerger, M.; Pervan, B.; Bouvet, D. Baseline Advanced RAIM User Algorithm: Proposed Updates. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 25–27 January 2022; pp. 229–251. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced RAIM user Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Wallner, S.; Fernandez, F.A.; Dellago, R.; Ioannides, R.; Hernandez, I.F.; Belabbas, B.; Spletter, A.; et al. Critical Elements for a Multi-Constellation Advanced RAIM. Navig. J. Inst. Navig. 2013, 60, 53–69. [Google Scholar] [CrossRef]
- Todd, W.; Enge, P. Weighted RAIM for Precision Approach. In Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995; pp. 1995–2004. [Google Scholar]
- Joerger, M.; Zhai, Y.; Martini, I.; Blanch, J.; Pervan, B. ARAIM Continuity and Availability Assertions, Assumptions, and Evaluation Methods. In Proceedings of the 2020 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 21–24 January 2020; pp. 404–420. [Google Scholar] [CrossRef]
- GALILEO—Open Service—Service Definition Document, Issue 1.3, November 2023. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-OS-SDD_v1.3.pdf (accessed on 21 March 2024).
- Global Positioning System—Standard Positioning Service—Performance Standard, 4th ED., September 2008. Available online: https://www.gps.gov/technical/ps/2008-SPS-performance-standard.pdf (accessed on 21 March 2024).
- Phelts, R.E.; Blanch, J.; Chen, Y.H.; Enge, P. ARAIM in Flight Using GPS and GLONASS: Initial Results from a Real-time Implementation. In Proceedings of the 29th International Technical Meeting of the ION Satellite Division (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar] [CrossRef]
- Rippl, M.; Martini, I.; Belabbas, B.; Meurer, M. ARAIM Operational Performance Tested in Flight. In Proceedings of the 2014 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 27–29 January 2014. [Google Scholar]
- The DREAMS Project, SESAR VLD1-W2. Available online: https://www.sesarju.eu/projects/DREAMSVLD (accessed on 21 March 2024).
- Caccioppoli, N.; Duchet, D.; Lipp, A. DFMC GBAS Processing of Flight Trial Data—A First Comparison of Options. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023. [Google Scholar] [CrossRef]
- Working Group C, ARAIM Technical Subgroup, Milestone 3 Report, 26 February 2016. Available online: https://ec.europa.eu/newsroom/growth/items/48690/en (accessed on 21 March 2024).
- EUROCAE ED-259A Minimum Operational Performance Standards for Dual Frequency Multi Constellation Satellite Based Augmentation System Airborne Equipment, Revision A, 11 October 2023. Available online: https://www.eurocae.net/news/posts/2023/october/ed-259a-minimum-operational-performance-standard-for-dual-frequency-multi-constellation-satellite-based-augmentation-system-airborne-equipment/ (accessed on 21 March 2024).
- Proposals for the Amendment of ICAO Annex 10, Volume I and Volume V Related to the global navigation satellite system (GNSS) and OTHER Navigation Aids, 31 October 2023; Developed by the Seventh Meeting of the Navigation Systems Panel (NSP/7). Available online: https://news.mcaa.gov.mn/uploads/bookSubject/2024-01/65b9ee42b8df1.pdf (accessed on 21 March 2024).
- International Civil Aviation Organization (ICAO). Performance-Based Navigation (PBN) Manual Doc 9613, 2nd ed.; 2023; Available online: https://www.icao.int/ESAF/Documents/meetings/2023/PBN%20ROUTE%20LAB%2022-26%20May%202023/Presentations/prl_changes%20to%20icao%20doc9613.pdf (accessed on 21 March 2024).
- Canadian Spatial Reference System Precise Point Positioning (CSRS-PPP). Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php/ (accessed on 9 January 2024).
- Circiu, M.S.; Caizzone, S.; Felux, M.; Enneking, C.; Rippl, M.; Meurer, M. Development of the dual-frequency dual-constellation airborne multipath models. Navig. J. Inst. Navig. 2020, 67, 61–81. [Google Scholar] [CrossRef]
- Circiu, M.-S.; Caizzone, S.; Felux, M.; Enneking, C.; Meurer, M. Improved Airborne Multipath Modelling. In Proceedings of the 31st International Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar] [CrossRef]
- Thomas, J.J.; Klobuchar, R.A.; Enge, P. Scintillation prediction and effects on GPS receiver phase tracking loop performance. Int. Organ. Navig. (ION) 1993, 40, 75–190. [Google Scholar]
- RTCA DO-293B Minimum Operational Performance Standards for Required Navigation Performance for Area Navigation. 15 December 2015.
- Blanch, J.; Walter, T.; Enge, P. Fixed Subset Selection to Reduce Advanced RAIM Complexity. In Proceedings of the 2018 International Technical Meeting of The Institute of Navigation, Reston, VA, USA, 29 January–1 February 2018. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caccioppoli, N.; Duchet, D.; Berz, G. Evaluation of H-ARAIM Reference Algorithm Performance Using Flight Data. Eng. Proc. 2025, 88, 1. https://doi.org/10.3390/engproc2025088001
Caccioppoli N, Duchet D, Berz G. Evaluation of H-ARAIM Reference Algorithm Performance Using Flight Data. Engineering Proceedings. 2025; 88(1):1. https://doi.org/10.3390/engproc2025088001
Chicago/Turabian StyleCaccioppoli, Natali, David Duchet, and Gerhard Berz. 2025. "Evaluation of H-ARAIM Reference Algorithm Performance Using Flight Data" Engineering Proceedings 88, no. 1: 1. https://doi.org/10.3390/engproc2025088001
APA StyleCaccioppoli, N., Duchet, D., & Berz, G. (2025). Evaluation of H-ARAIM Reference Algorithm Performance Using Flight Data. Engineering Proceedings, 88(1), 1. https://doi.org/10.3390/engproc2025088001





