Repercussions on the Shear Force of an Internal Beam–Column Connection from Two Symmetrical Uniformly Distributed Loads at Different Positions on the Beam †
Abstract
1. Introduction
2. Materials
3. Method
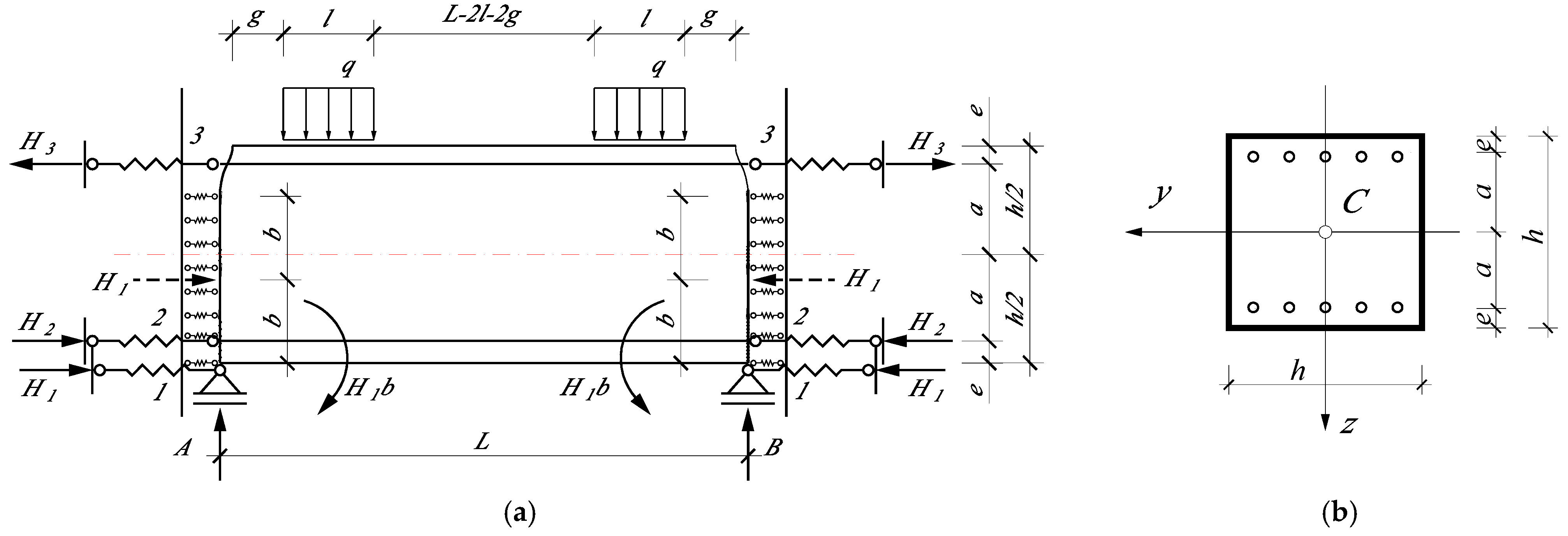
3.1. Support Reactions with Axial Force in the Strain Energy Expression
3.2. Support Reactions Without Axial Force in Strain Energy Expression
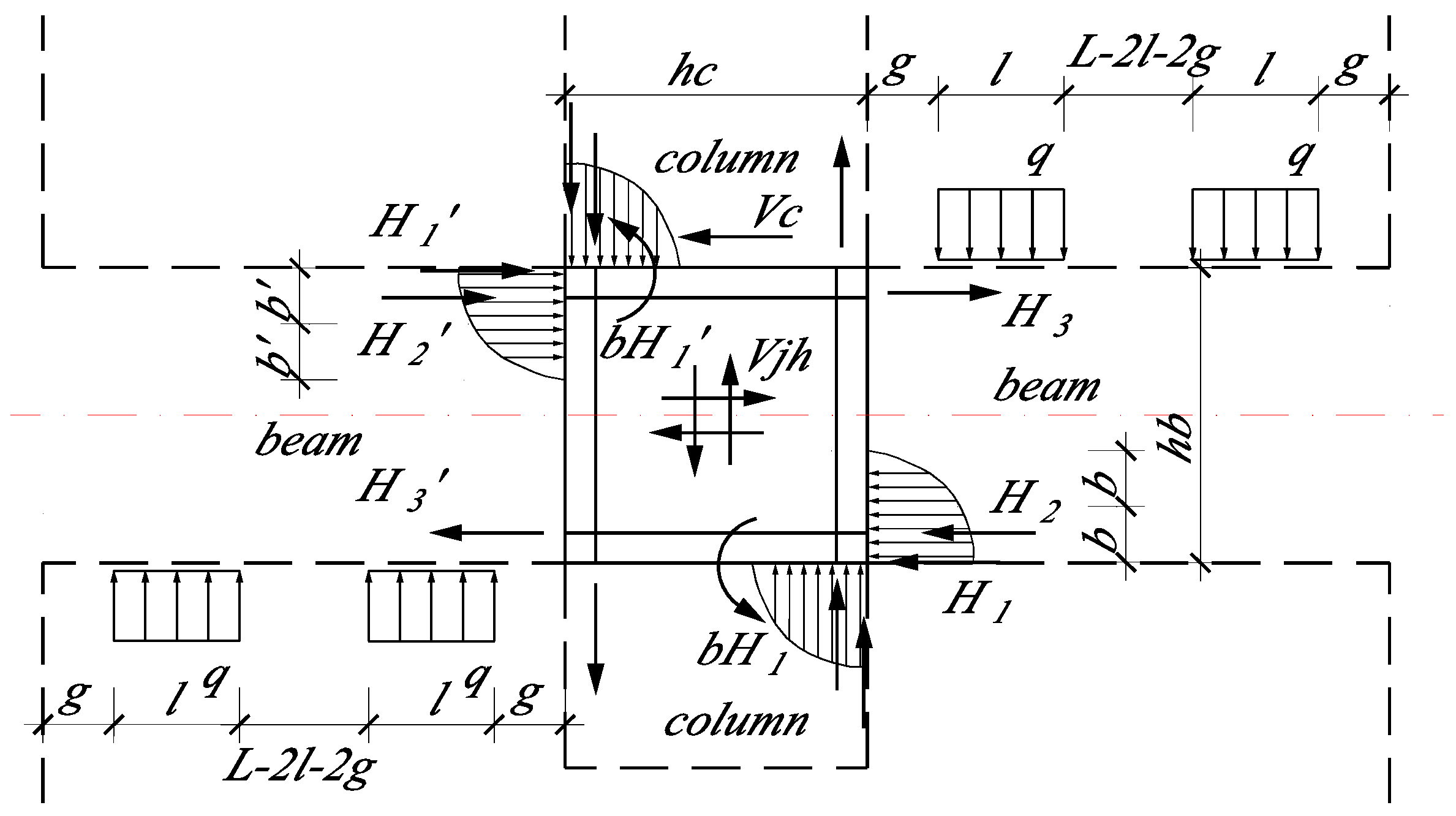
4. Results and Discussion
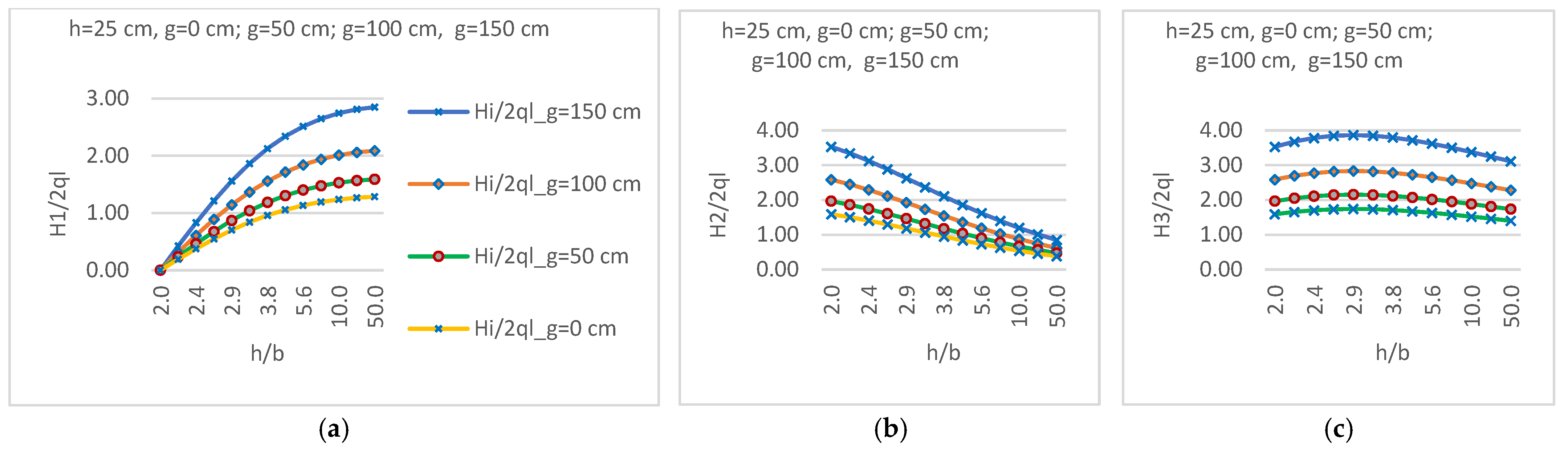
4.1. Comparison of Support Reaction Magnitude Results for Case I, Case II, and Case III
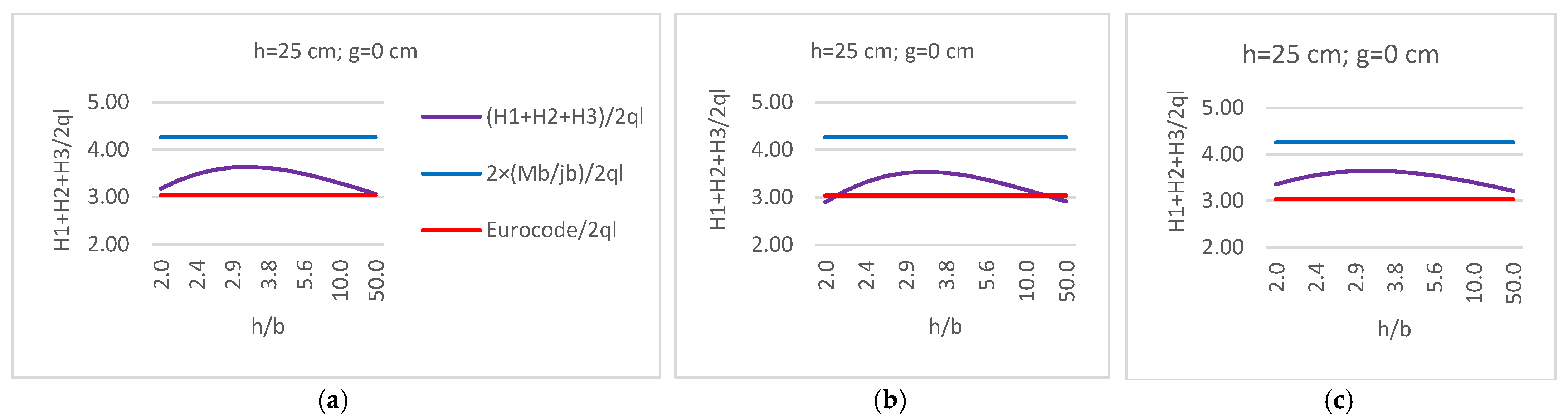
4.2. Comparison of the Results from Equation (2), Equation (10), and Eurocode
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hanson, N.W.; Connor, H.W. Seismic Resistance of Reinforced Concrete Beam-Column Joint. J. Struct. Div. 1967, 93, 533–560. [Google Scholar] [CrossRef]
- Park, R.; Keong, Y.S. Test on structural concrete beam-column joints with intermediate column bars. Bull. New Zealand Natl. Soc. Earthq. Eng. 1979, 12, 189–203. [Google Scholar] [CrossRef]
- Paulay, T. Equilibrium criteria for reinforced-concrete beam-column joints. ACI Struct J. 1989, 86, 635–643. [Google Scholar]
- Park, R. A Summary of Results of Simulated Seismic Load Tests on Reinforced Concrete Beam-Column Joints, Beams and Columns with Substandard Reinforcing Details. J. Earthq. Eng. 2002, 6, 147–174. [Google Scholar] [CrossRef]
- Javad, S.; Bengar, H.A.; Parvin, A. Analytical prediction of seismic behavior of RC joints and columns under varying axial load. Eng. Struct. 2018, 174, 792–813. [Google Scholar] [CrossRef]
- Gombosuren, D.; Maki, T. Prediction of Joint Shear Deformation Index of RC Beam–Column Joints. Buildings 2020, 10, 176. [Google Scholar] [CrossRef]
- Hayat, K.F.; Tahir, M.F.; Khan, Q.Z. Numerical simulation and performance evaluation of beam column joints containing FRP bars and wire mesh arrangements. J. Mech. Contin. Math. Sci. 2021, 16, 112–130. [Google Scholar] [CrossRef]
- Kalogeropoulos, G.; Tsonos, A.-D.; Iakovidis, P. Hysteresis Behavior of RC Beam–Column Joints of Existing Substandard RC Structures Subjected to Seismic Loading–Experimental and Analytical Investigation. Buildings 2024, 14, 1609. [Google Scholar] [CrossRef]
- Kim, J.; LaFave, J.M. Key infuence parameters for the joint shear behaviour of reinforced concrete (RC) beam–column connections. Eng. Struct. 2007, 29, 2523–2539. [Google Scholar] [CrossRef]
- Shafaei, J.; Zareian, M.S.; Hosseini, A.; Marefat, M.S. Effects of joint flexibility on lateral response of reinforced concrete frames. Eng. Struct. 2014, 81, 412–413. [Google Scholar] [CrossRef]
- Ramaglia, G.; Lignola, G.P.; Fabbrocino, F.; Prota, A. Unified Simplified Capacity Model for Beam-Column Joints into RC Moment Resisting Frame. Appl. Sci. 2022, 12, 10709. [Google Scholar] [CrossRef]
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004; Volume 1, p. 231.
- Barbagallo, F.; Bosco, M.; Ghersi, A.; Marino, E.M.; Sciacca, F. A simple but effective capacity model for check and design of beam-column joints in RC seismic buildings. Procedia Struct. Integr. 2023, 44, 363–370. [Google Scholar] [CrossRef]
- Shiohara, H. New model for shear failure of RC interior beam-column connection. J. Struct. Eng. 2001, 127, 152–160. [Google Scholar] [CrossRef]
- Fardis, M.N. Shear strength model for RC joints, consistent with the shear design rules for prismatic members in the second-generation Eurocodes. Bull Earthq. Eng 2021, 19, 889–917. [Google Scholar] [CrossRef]
- Floridia, A.; Panarelli, D.; Rossi, P.P.; Spinella, N. Simplified evaluation of the shear strength of slender rectangular R.C. members with shear reinforcement. Procedia Struct. Integr. 2023, 44, 504–511. [Google Scholar] [CrossRef]
- Nicoletti, V.; Carbonari, S.; Gara, F. Beam-column joint nomogram: A simple and fast-to-use tool to evaluate the joint integrity in RC structures. Procedia Struct. Integr. 2023, 44, 371–377. [Google Scholar] [CrossRef]
- Angiolilli, M.; Gregori, A.; Tonelli, R.; Tonelli, C.; Ciuffetelli, E.; Peditto, A. Structural performance of unreinforced full-scale façade concrete beam-column joint under cyclic load. Procedia Struct. Integr. 2023, 44, 870–877. [Google Scholar] [CrossRef]
- Doicheva, A. Shear Force of Interior Beam–Column Joints under Symmetrical Loading with Two Transverse Forces on the Beam. Buildings 2024, 14, 3028. [Google Scholar] [CrossRef]
- Doicheva, A. Determination of the Shear Force in RC Interior Beam-Column Connections. Eurasia Proc. Sci. Technol. Eng. Math. 2023, 23, 361–371. [Google Scholar] [CrossRef]
- Doicheva, A. Distribution of Forces in RC Interior Beam–Column Connections. Eng. Proc. 2023, 56, 114. [Google Scholar] [CrossRef]
- Doicheva, A. Shear force in RC internal beam-column connections for a beam loaded with a transverse force occupying different possible positions. Eurasia Proc. Sci. Technol. Eng. Math. (EPSTEM) 2024, 29, 128–144. [Google Scholar] [CrossRef]
- Doicheva, A. Alteration of the Shear Force in an Internal Beam-Column Joint during the Initiation and Growth of a Crack in a Cantilever Beam. Procedia Struct. Integr. 2024, 66, 433–448. [Google Scholar] [CrossRef]
- Doicheva, A. Off-center supported beam with additional elastic supports, located along the height of the beam and loaded with a distributed transverse load. In Proceedings of the XXIII International Scientific Conference VSU’2023, Sofia, Bulgaria, 22–24 June 2023; Volume I, pp. 451–460. (In Bulgarian). [Google Scholar]
- Doicheva, A. Determination of Forces in an Internal Beam-Column Connection. Static Research; Dinev, D., Abdulahad, E., Eds.; Avangard Prima: Sofia, Bulgaria, 2024; p. 152. [Google Scholar]
- MATLAB, R2017b. The MathWorks Inc.: Natick, MA, USA, 2017.
- Doicheva, A.; Shu, Y.; Kusuhara, F.; Shiohara, H. Seismic tests on reinforced concrete beam-column joint sub-assemblages subject to lateral and long-term vertical load. Struct. Integr. Life 2023, 23, 269–276. [Google Scholar]
- RuckZuck, Version 4.0. Mursoft Wörgötter, Kump OEG: Graz, Austria, 2015.


| Case I | Case II | Case III | ||||
|---|---|---|---|---|---|---|
| Value [kN] | Value [kN] | % Relative to Case I | Value [kN] | % Relative to Case I | ||
| 0 | 0 | 0 | - | 0 | - | |
| 2.9 | 311.31 | 410.50 | 31.86 | 205.30 | −34.05 | |
| 50 | 569.90 | 668.46 | 17.29 | 433.35 | −23.96 | |
| 0 | 705.43 | 643.31 | −8.81 | 745.37 | 5.66 | |
| 2.9 | 525,38 | 434.53 | −17.29 | 616.77 | 17.39 | |
| 50 | 169.60 | 82.75 | −51.21 | 308.21 | 81.73 | |
| 0 | 705.43 | 643.31 | −8.81 | 745.37 | 5.66 | |
| 2.9 | 772.82 | 716.62 | −7.27 | 795.49 | 2.93 | |
| 50 | 622.57 | 542.10 | −12.93 | 685.45 | 10.10 | |
| Case I | 0 | 16.35 | −56.94 |
| 3.3 | 1.66 | −62.38 | |
| 50 | 20.52 | −55.40 | |
| Case II | 0 | 27.59 | −52.78 |
| 3.3 | 4.48 | −61.34 | |
| 50 | 26.93 | −53.03 | |
| Case III | 0 | 10.12 | −59.25 |
| 3.3 | 1.28 | −62.52 | |
| 50 | 15.03 | −57.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doicheva, A. Repercussions on the Shear Force of an Internal Beam–Column Connection from Two Symmetrical Uniformly Distributed Loads at Different Positions on the Beam. Eng. Proc. 2025, 87, 85. https://doi.org/10.3390/engproc2025087085
Doicheva A. Repercussions on the Shear Force of an Internal Beam–Column Connection from Two Symmetrical Uniformly Distributed Loads at Different Positions on the Beam. Engineering Proceedings. 2025; 87(1):85. https://doi.org/10.3390/engproc2025087085
Chicago/Turabian StyleDoicheva, Albena. 2025. "Repercussions on the Shear Force of an Internal Beam–Column Connection from Two Symmetrical Uniformly Distributed Loads at Different Positions on the Beam" Engineering Proceedings 87, no. 1: 85. https://doi.org/10.3390/engproc2025087085
APA StyleDoicheva, A. (2025). Repercussions on the Shear Force of an Internal Beam–Column Connection from Two Symmetrical Uniformly Distributed Loads at Different Positions on the Beam. Engineering Proceedings, 87(1), 85. https://doi.org/10.3390/engproc2025087085






