Methods for Processing Signal Conversion in Velocity and Acceleration Measurement Considering Transducer Characteristics ^†

Abstract

This study presents an innovative approach to processing vibration signals in bridge structures, with a focus on enhancing the accuracy of dynamic response measurements and structural health assessments. It addresses key challenges in signal processing, particularly the uncertainties in selecting filtering parameters for isolating dynamic components from static displacements. A novel method for adaptive filter parameter selection is proposed, which considers variations in resonant frequencies and the non-linearity of quasi-static displacements caused by moving loads. This approach significantly reduces errors in determining forced and natural vibration parameters, leading to more accurate assessments of the bridge’s mechanical characteristics. The study introduces an optimized algorithm for processing acceleration and velocity signals, improving the resolution of natural frequency identification. This method combines traditional Fast Fourier Transform (FFT) techniques with an innovative spectral analysis approach, enabling precise identification of resonant frequencies and damping coefficients. A comprehensive evaluation framework is developed, integrating vibration amplitude, frequency, and damping ratio analyses. This framework enhances structural health assessments, improving the detection and characterization of potential defects and changes in load-bearing capacity. The practical significance of this research lies in its real-world application to bridge diagnostics. The study provides guidelines for sensor selection and configuration, adapted for various bridge types and sizes. The proposed methods demonstrate notable improvements in dynamic coefficient determination and overall structural assessments, offering the potential to reduce maintenance costs and enhance bridge safety.

1. Introduction

Ensuring the structural health of bridges is a critical component of maintaining transportation infrastructure. Bridges, as vital elements of urban and interurban connectivity, must meet the growing demands of load capacity and durability while operating under increasingly complex environmental and operational conditions. Regular diagnostics and monitoring allow for the timely identification of defects, ensuring safety and prolonging the operational lifespan of these structures.

Dynamic testing has emerged as a powerful tool in bridge diagnostics. It provides key insights into the mechanical properties of bridges, such as natural frequencies, damping coefficients, and dynamic load factors. These parameters are essential for detecting structural defects, monitoring performance, and predicting long-term durability. However, the complexity of vibration signal processing introduces significant challenges to the accuracy and reliability of these assessments.

One of the primary challenges lies in separating dynamic components from quasi-static displacements caused by moving loads. This issue is further compounded by the non-linearity of structural responses and uncertainties in determining the filtering parameters required for isolating vibration signals. Traditional methods often rely on fixed filtering techniques, which can introduce errors when the resonant frequencies of the structure vary under different load conditions, leading to misinterpretation of vibration characteristics and inaccuracies in structural assessments. To address this, we propose an adaptive filtering approach that dynamically adjusts filtering parameters based on real-time spectral analysis, ensuring optimal signal isolation. Additionally, we integrate spectral refinement and FEM-based validation to improve resonance frequency detection, leading to more accurate dynamic parameter estimation. Unlike previous methods, which either rely solely on filtering or independent FEM analysis, our framework leverages a hybrid approach that enhances both noise reduction and structural assessment accuracy. Furthermore, the accuracy of vibration measurements is inherently influenced by the performance of sensors, such as accelerometers and velocity transducers. Their frequency response limitations and sensitivity constraints may introduce distortions in the measured signals, particularly in the presence of external noise [1,2].

Innovative methodologies, such as adaptive filtering and advanced spectral analysis, have been proposed to address these challenges [3,4,5]. Recent advancements in computational tools, including finite element modeling and machine learning, have further enhanced the precision of bridge diagnostics [6,7]. These methods allow for the dynamic adjustment of filtering parameters, accommodating the variability of resonant frequencies and reducing errors associated with quasi-static displacement components [8,9].

This study introduces an optimized framework for processing vibration signals by uniquely integrating adaptive filtering, spectral refinement, and finite element modeling (FEM). Unlike previous studies that apply these techniques separately, our approach combines them into a unified framework that dynamically adjusts filtering parameters, improves frequency resolution, and enhances modal parameter estimation. The use of FEM not only validates theoretical predictions but also bridges the gap between numerical simulations and experimental results. Furthermore, our methodology is experimentally verified using real-world bridge diagnostics, demonstrating its practical applicability and robustness in structural health monitoring. This approach enhances diagnostic precision and provides practical recommendations for sensor placement and configuration tailored to diverse bridge types and operational conditions [10,11,12].

Practical applications of these methods include early defect detection, cost-efficient maintenance planning, and enhanced safety through real-time monitoring of structural performance. Such advancements align with recent studies on structural health monitoring systems, which emphasize the importance of accurate diagnostics for preventing catastrophic failures [13,14].

2. Materials and Methods

This study develops an advanced methodology for processing vibration signals in bridge structures to enhance the accuracy of structural health assessment. High-sensitivity accelerometers and velocity transducers were employed to record dynamic responses, ensuring reliable data collection across a wide frequency range. Sensor placement was optimized based on modal analysis to identify zones of maximum dynamic response, minimizing noise interference and enhancing the quality of the recorded signals [15,16].

Raw acceleration and velocity signals were preprocessed using adaptive filtering to remove noise and quasi-static components caused by moving loads.

The adaptive filter dynamically adjusts its parameters using the equation

$$H\left(f\right)={\displaystyle \frac{1}{1+{\left(\frac{f}{f_c}\right)}^n}},$$

(1)

where $H\left(f\right)$ is the filter transfer function, $f_c$ is the cutoff frequency, and n is the filter order.

The cutoff frequency and filter order were initially estimated based on theoretical spectral analysis of the measured vibration signals. To refine these values, we conducted an empirical study using real bridge vibration data, comparing various filter settings to minimize signal distortion while preserving dynamic components. Additionally, these parameters were further refined through an iterative process to achieve the best balance between noise reduction and signal fidelity. The final parameters were selected based on the minimization of high-frequency noise while retaining critical modal information.

This approach ensured that low-frequency noise was suppressed while preserving the integrity of dynamic components for further analysis.

Spectral decomposition of the signals was performed using the Fast Fourier Transform, described by

$$X\left(f\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi fn/N},$$

(2)

where $X\left(f\right)$ represents the frequency-domain signal, $x\left(n\right)$ is the time-domain signal, and N is the number of samples. An advanced spectral refinement algorithm was applied to enhance resolution, enabling precise identification of natural frequencies, damping coefficients, and vibration amplitudes [17].

A finite element model was developed to simulate the dynamic behavior of the bridge under various loading conditions.

The FEM incorporated detailed material properties, boundary conditions, and geometric configurations based on AASHTO LRFD bridge design specifications [16] and was supplemented by empirical data collected from real bridge structures. The material properties, including elasticity modulus, damping coefficients, and density, were taken from standard engineering references and validated using available field measurements. Boundary conditions were set according to typical bridge support configurations as specified in the AASHTO guidelines, ensuring consistency with practical engineering applications.

The governing equation of motion used in the FEM was

$$M\ddot{u}\left(t\right)+C\dot{u}\left(t\right)+Ku\left(t\right)=F\left(t\right),$$

(3)

where M is the mass matrix, C is the damping matrix, K is the stiffness matrix, $u\left(t\right)$ is the displacement vector, $F\left(t\right)$ is the external force vector.

This equation models the dynamic response of the bridge under external excitations, providing a reference for comparison with the experimental results [16].

Additionally, the structural performance was evaluated using established criteria: Allowable Stress Design (ASD)—Evaluates stress levels within the structure to ensure they remain below allowable limits [15,16]. Load Factor Design (LFD)—Considers safety factors for different load types, accounting for uncertainties in material properties and external forces [18]. Load and Resistance Factor Design (LRFD)—Integrates load and resistance factors, ensuring a comprehensive evaluation by addressing variability in loads and material resistance [16]. Bridge Diagnostics Inc. (BDI) Criteria—Developed for analyzing bridge performance using load testing and dynamic response data [17]. The structural reserve factor ($RF$) was calculated as follows:

$$RF={\displaystyle \frac{S_s-S_{DL}}{S_{LL,I}}},$$

(4)

where $S_s$ is the allowable (limit) stress, $S_{DL}$ is the stress caused by applied loads considering dynamic effects, $S_{LL,I}$ is the stress caused by live loads.

$RF$ represents the safety margin under applied loads. This criterion ensures that the bridge operates safely under both dynamic and static conditions.

The Load Factor Design (LFD) method is employed to evaluate the load-carrying capacity of bridge elements under applied loads, accounting for safety factors. The formula used to calculate LFD is given by

$$LF={\displaystyle \frac{C-1.3·DL}{2.17·LL·(1+I)}},$$

(5)

where C is the load-carrying capacity of the bridge element, $DL$ is the dead load applied to the structure, $LL$ is the live load acting on the structure, I is the dynamic effect coefficient, representing the impact of dynamic forces [16].

This formula considers both static and dynamic effects, ensuring the bridge’s safety under realistic loading conditions.

The Load and Resistance Factor (LRF) was calculated to account for the interaction between various loads and resistance factors:

$$LRF={\displaystyle \frac{C-{\gamma }_{DC}·DC-{\gamma }_{DW}·DW+{\gamma }_P·P}{{\gamma }_L·L·(1+IM)}},$$

(6)

where $DC$ is the static load, $DW$ is the fatigue load, P is the permanent load, L is the applied load, ${\gamma }_{DC}$, ${\gamma }_{DW}$, ${\gamma }_P$, and ${\gamma }_L$ are the respective load coefficients, $IM$ is the permissible dynamic load coefficient.

The carrying capacity (C) of the structural element was calculated either based on allowable stresses or ultimate resistance, given by

$$C={\varphi }_c·{\varphi }_s·\varphi ·R,$$

(7)

or

$$C=S_s,$$

(8)

where ${\varphi }_c$ is the condition factor, ${\varphi }_s$ is the system factor, $\varphi$ is the resistance factor, R is the ultimate resistance.

The structural performance evaluation based on the BDI system utilizes the following formula:

$$B{D}_S={\displaystyle \frac{C-{\gamma }_{DL}·DL}{{\gamma }_{LL}·LL·(1+I)}},$$

(9)

where C is the load-carrying capacity, ${\gamma }_{DL}$ is the load coefficient for destructive loads, $DL$ is the destructive load, ${\gamma }_{LL}$ is the load coefficient for applied loads, $LL$ is the applied load, I is the dynamic effect coefficient.

This criterion evaluates the structural state and capacity under both static and dynamic conditions. The results of calculations using this criterion provide insights into the safety margin and load-carrying capacity of the bridge under various load scenarios.

These formulas comprehensively describe the interaction of loads and resistances, providing a robust framework for evaluating bridge performance under dynamic and static conditions.

Field experiments were conducted to verify the proposed methodology. Controlled dynamic loading tests were performed, including vehicular movements and environmental excitations. These experiments measured key parameters such as deflections, stresses, and accelerations at multiple points along the bridge. Measurements were processed using the proposed framework to extract dynamic parameters, including natural frequencies, damping ratios, and vibration amplitudes.

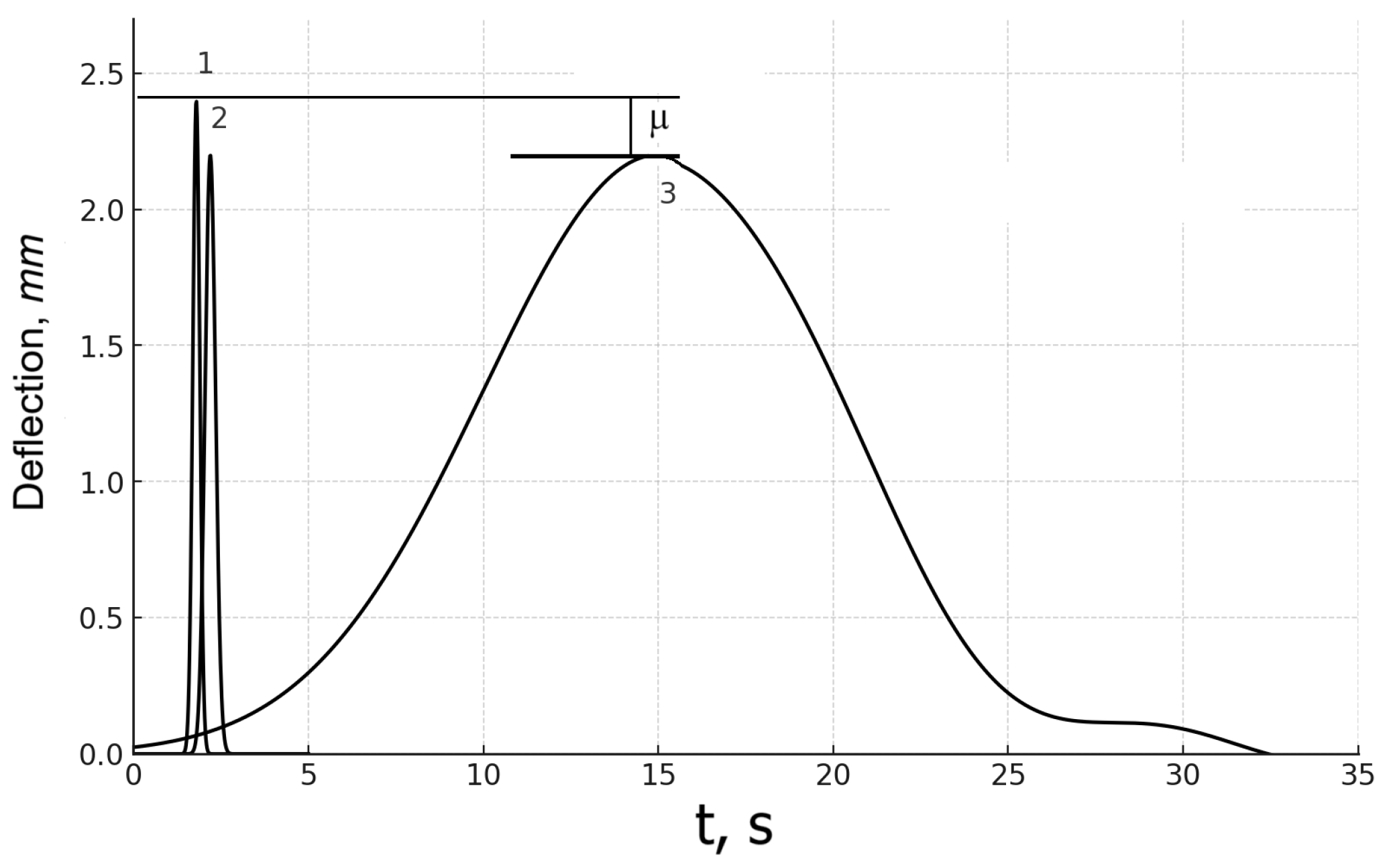
The Dynamic Load Factor (DLF), a crucial parameter for assessing structural performance under dynamic loads, was calculated as

$$\mu ={\displaystyle \frac{{\Delta }_D}{{\Delta }_S}},$$

(10)

where ${\Delta }_D$ is the dynamic displacement and ${\Delta }_S$ is the static displacement.

This ratio quantifies the amplification of the structural response due to dynamic effects compared to static conditions [16,17].

Finally, an error analysis was performed to evaluate the accuracy of the proposed methodology. The errors were quantified using the formula:

$$E={\displaystyle \frac{\left|P_{\mathrm{measured}}-P_{\mathrm{reference}}\right|}{P_{\mathrm{reference}}}}\times 100$$

(11)

where $P_{\mathrm{measured}}$ and $P_{\mathrm{reference}}$ represent the measured and reference values of dynamic parameters, respectively.

The results demonstrated a significant reduction in errors compared to traditional approaches, confirming the effectiveness of adaptive filtering and advanced spectral analysis techniques.

By combining computational modeling, experimental validation, and advanced signal processing, this study provides a robust framework for bridge diagnostics. The proposed methodology significantly improves the accuracy of structural health monitoring, offering engineers practical tools for ensuring the safety and durability of bridge structures.

3. Results

The obtained results confirm the reliability of the proposed methodology for evaluating bridge structures based on vibration signal processing and finite element modeling. The findings provide key insights into structural response, dynamic load effects, and safety assessment.

The experimental measurements of displacements under static and dynamic loading conditions revealed significant variations depending on vehicle speed. The results demonstrated that quasi-static deformations correlated directly with the position of the moving load, while dynamic responses were more influenced by resonance effects and structural stiffness.

The spectral analysis using FFT identified dominant vibration frequencies in the range of 3 Hz–12 Hz, corresponding to the bridge’s natural frequencies. At speeds above 100 km/h, shifts in peak frequencies were observed, indicating the presence of resonance effects. These findings emphasize the need to account for speed-dependent dynamic factors when evaluating structural integrity.

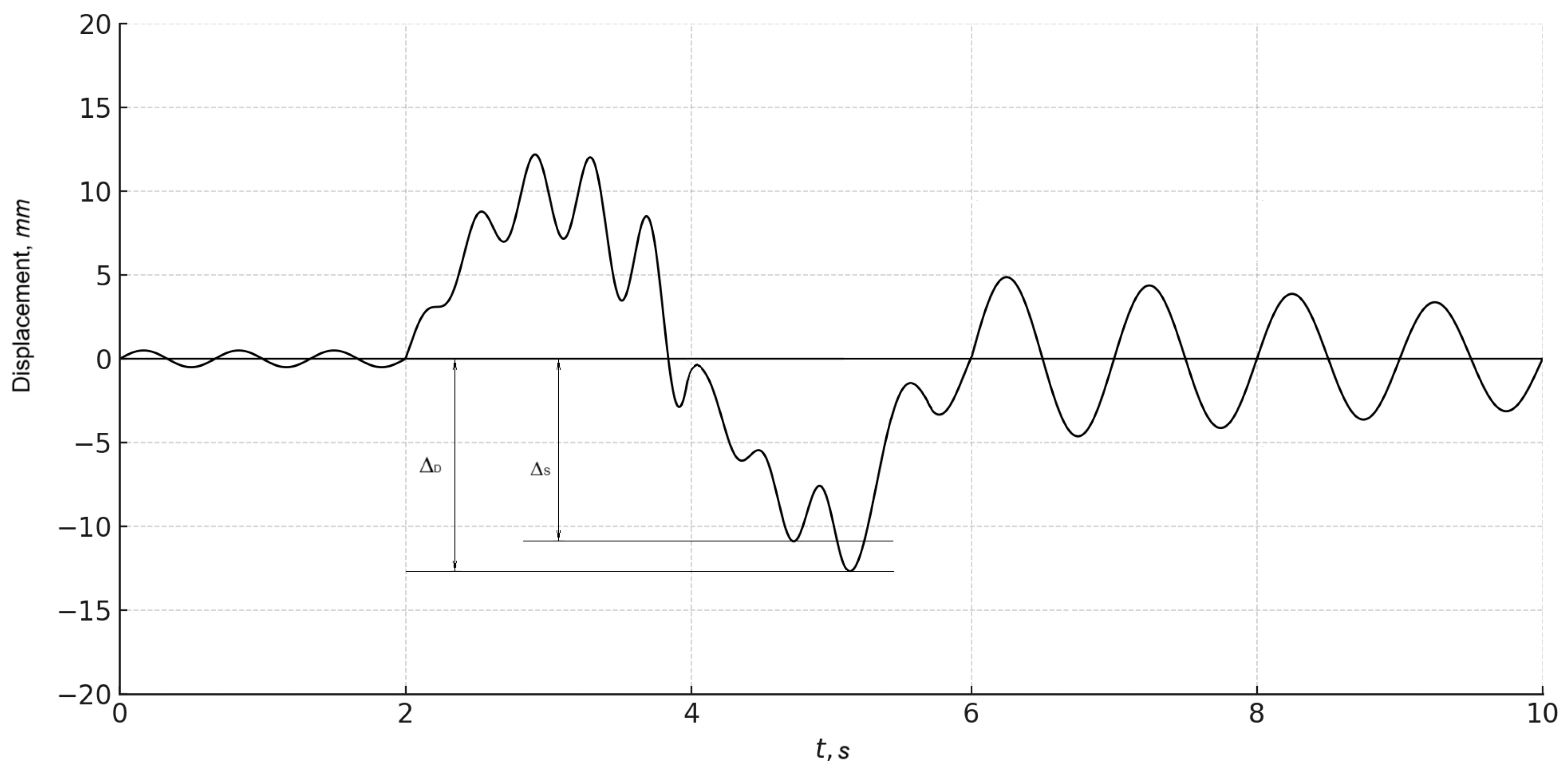
Figure 1 presents the measured displacement results, demonstrating how bridge deflections vary under dynamic loading. The data indicate that at lower speeds, the structural response remains relatively stable, while at higher speeds, the oscillatory behavior of the bridge intensifies.

Figure 2 further illustrates displacement measurements under varying loading conditions, confirming that dynamic amplification increases as vehicle speed rises. This observation aligns with the calculated Dynamic Load Factor, which varied from 1.05 to 1.45, emphasizing the significance of dynamic influences in bridge performance evaluation.

The identified frequency range (3 Hz–12 Hz) aligns with typical natural frequencies of medium-span bridges. Deviations from this range could indicate material degradation, changes in boundary conditions, or structural defects. Notably, shifts in peak frequencies at vehicle speeds exceeding 100 km/h highlight the presence of resonance effects, which can amplify stress cycles and accelerate fatigue damage. These findings suggest that bridge design should account for resonance conditions through tuned damping mechanisms or structural reinforcements. Additionally, the observed DLF range of 1.05 to 1.45 confirms that structural response significantly varies with loading conditions and vehicle speeds. These values indicate that dynamic effects must be incorporated into design safety margins to ensure long-term durability. The results emphasize the necessity of periodic monitoring and load factor assessments to detect performance changes that could compromise bridge safety.

The finite element modeling results closely matched the experimental measurements, validating the numerical approach. The observed stress distribution and deformation patterns were consistent with field tests, confirming the model’s predictive accuracy. The structural safety assessment, performed according to Allowable Stress Design (ASD), Load Factor Design (LFD), and Load and Resistance Factor Design (LRFD), indicated compliance with AASHTO LRFD standards under normal traffic conditions.

The error analysis showed that the deviation between experimental and FEM-predicted results was within ±5% for modal frequencies and ±7% for displacements. The primary error sources included environmental influences (temperature variations, wind effects), minor inaccuracies in sensor calibration, and nonlinearities in structural response.

Overall, the results demonstrate that the proposed methodology offers a precise and practical approach for evaluating bridge safety and durability, integrating computational modeling, experimental validation, and advanced signal processing techniques.

4. Conclusions

This study established a reliable framework for assessing the structural health of bridges by integrating advanced signal processing, spectral analysis, and finite element modeling. The proposed methodology demonstrated its effectiveness in capturing critical dynamic behaviors, including resonance effects and load amplification, which are essential for ensuring bridge safety.

The key findings emphasize the importance of addressing speed-dependent dynamic factors. The results indicate that higher vehicle speeds (>100 km/h) significantly amplify structural responses, increasing the dynamic load factor up to 1.45. These findings underscore the necessity of incorporating dynamic considerations into bridge design and evaluation to account for real-world traffic conditions.

Finite element modeling was validated through close agreement with the experimental results, providing a robust predictive tool for assessing stress distributions and modal frequencies. Importantly, compliance with AASHTO LRFD standards was confirmed, demonstrating that the structure meets safety and operational reliability requirements under both static and dynamic loads.

This research highlights the practical applicability of the developed methodology for real-world bridge diagnostics, enabling more accurate and efficient evaluations of structural performance. By reducing errors and improving diagnostic precision, this approach contributes to optimizing maintenance strategies and prolonging the lifespan of critical infrastructure.

Further exploration into the long-term effects of fatigue accumulation in bridge elements is necessary to enhance the reliability of structural health assessments. Fatigue-related degradation results from repeated dynamic loading, leading to progressive crack formation and reductions in structural stiffness over time. These changes manifest as frequency shifts and increased damping, which can serve as early indicators of fatigue damage. Future research should focus on developing advanced fatigue prediction models based on real-time vibration monitoring. The findings provide a valuable foundation for advancing bridge diagnostic techniques and ensuring infrastructure resilience.