Influence of Optical Feedback Strength on Intensity Noise and Photon Number Probability Distribution of InGaAsP/InP Laser †
Abstract
1. Introduction
2. Simulation Model
3. Simulation Results and Discussions
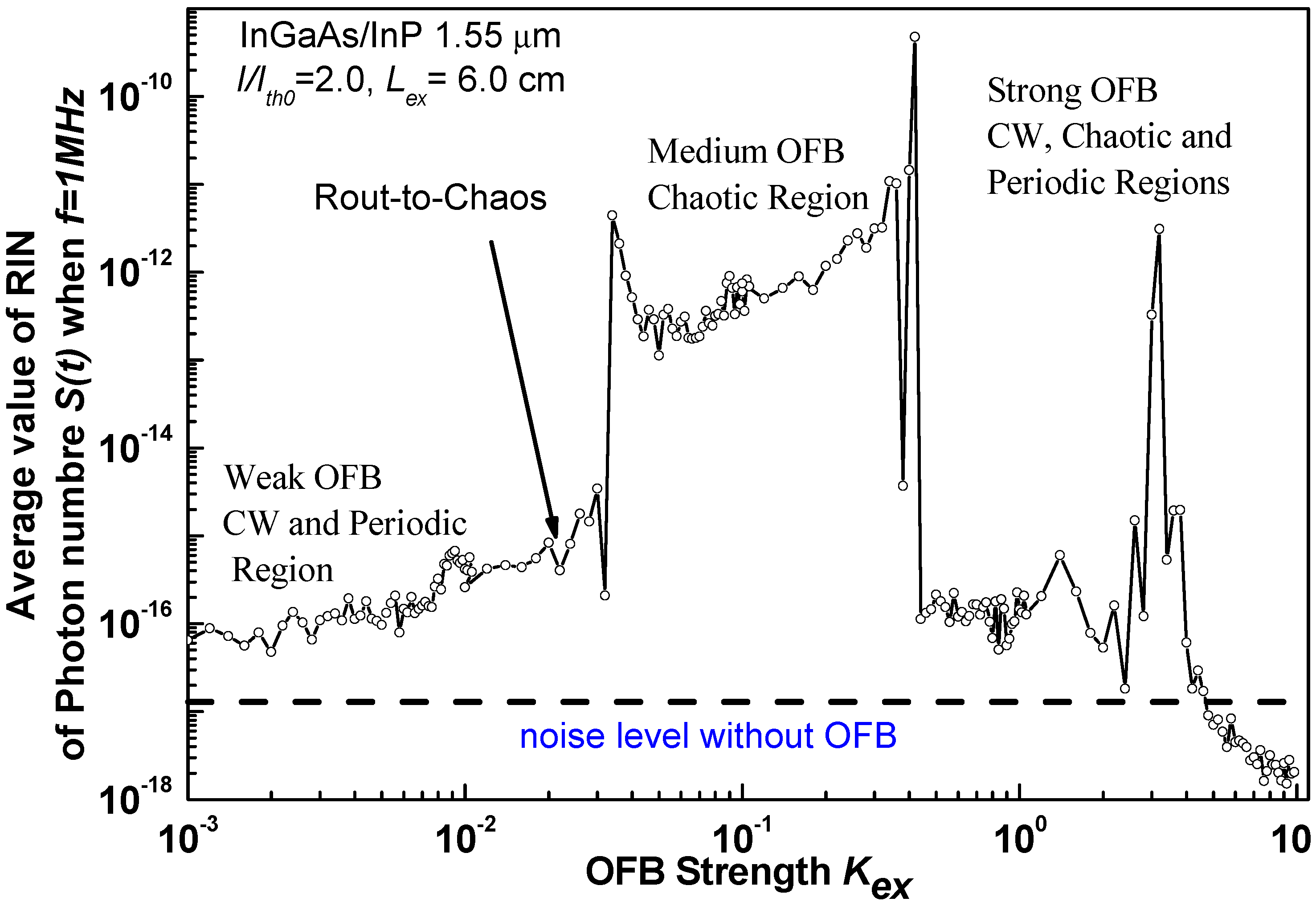
3.1. Bifurcation Diagrams
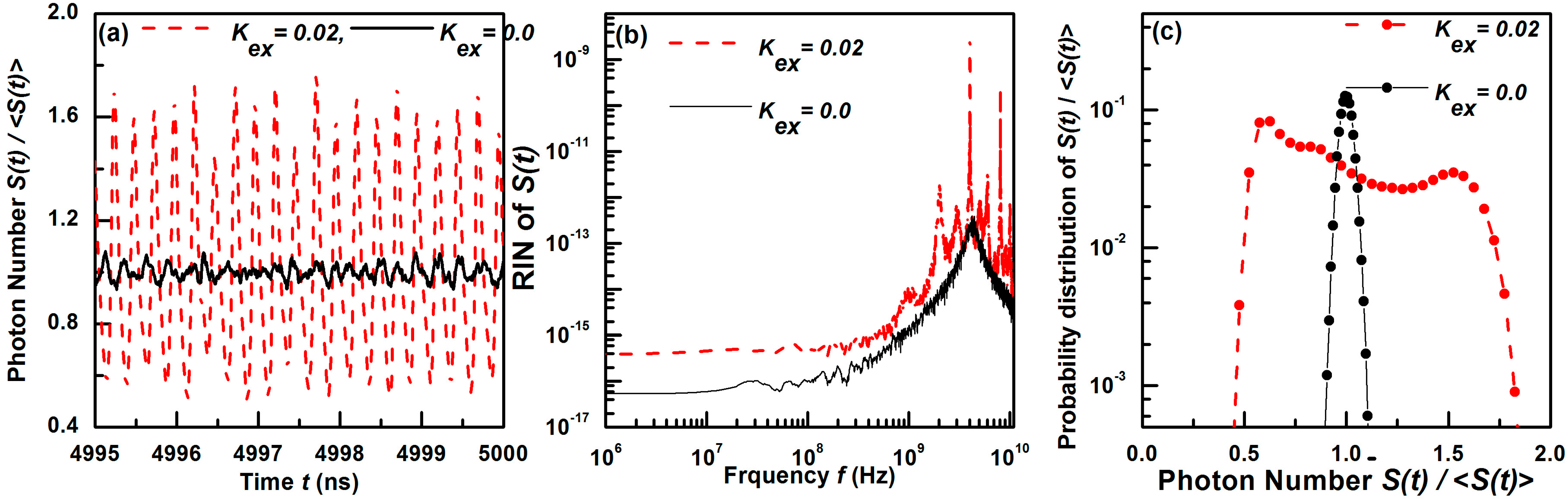
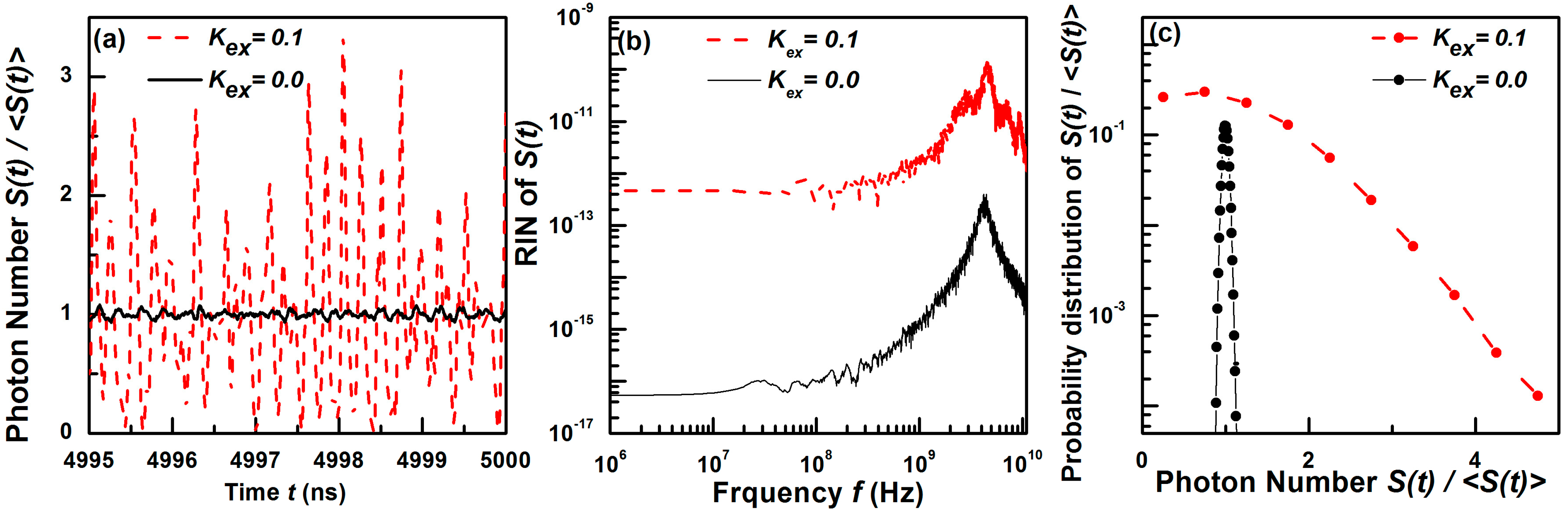
3.2. Time Variation, RIN, and PNPDD of S(t) for Different Operations of the SL
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agrawal, G.P.; Dutta, N.K. Semiconductor Lasers, 2nd ed.; Van Nostrand: New York, NY, USA, 1993. [Google Scholar]
- Mork, J.; Tromborg, B.; Mark, J. Chaos in semiconductor lasers with optical feedback: Theory and experiment. IEEE J. Quantum Electron. 1992, 28, 93–108. [Google Scholar] [CrossRef]
- Hohl, A.; Gavrielides, A. Bifurcation cascade in a semiconductor laser subject to optical feedback. Phys. Rev. Lett. 1999, 82, 1148–1151. [Google Scholar] [CrossRef]
- Kitaoka, Y.; Sato, H.; Mizuuchi, K.; Yamamoto, K.; Kato, M. Intensity noise of laser diodes with optical feedback. IEEE J. Quantum Electron. 1996, 32, 822–828. [Google Scholar] [CrossRef]
- Kallimani, K.; O’Mahony, M. Relative intensity noise for laser diodes with arbitrary amounts of optical feedback. IEEE J. Quantum Electron. 1998, 34, 1438–1446. [Google Scholar] [CrossRef]
- Mahmoud, S.W.Z.; Ahmed, M.; Hassan, A.M.A. Comprehensive large-signal analyses of RF modulation of vertical cavity surface emitting lasers. Opt. Laser Technol. 2013, 45, 406–413. [Google Scholar] [CrossRef]
- Meneghini, B.M.; Tazzoli, A.; Mura, G.; Meneghesso, G.; Zanoni, E. A review on the physical mechanisms that limit the reliability of GaN-based LEDs. IEEE Trans. Electron Devices 2009, 57, 108–118. [Google Scholar] [CrossRef]
- Olshansky, R.; Su, C.; Manning, J.; Powazinik, W. Measurement of radiative and nonradiative recombination rates in InGaAsP and AlGaAs light sources. IEEE J. Quantum Electron. 1984, 20, 838–854. [Google Scholar] [CrossRef]
- Hisham, H.K.; Mahdiraji, G.A.; Abas, A.F.; Mahdi, M.A.; Adikan, F.R.M. Characterization of turn-on time delay in a fiber grating Fabry–Perot lasers. IEEE Photonics J. 2012, 4, 1662–1678. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Ahmed, M.; Yamada, M. Influence of Nonlinear Gain and Nonradiative Recombination on the Quantum Noise in InGaAsP Semiconductor Lasers. Opt. Rev. 2002, 9, 260–268. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Ahmed, M.; Okamoto, T.; Ishimori, W.; Yamada, M. An improved analysis of semiconductor laser dynamics under strong optical feedback. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1265–1274. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Msmali, A.H. Numerical Analysis on the Impact of Optical Feedback and Nonlinear Gain on the Dynamics and Intensity Noise of Semiconductor Laser. Appl. Phys. B Lasers Opt. 2022, 128, 113. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347. [Google Scholar] [CrossRef]
- Hanzard, P.-H.; Talbi, M.; Mallek, D.; Kellou, A.; Leblond, H.; Sanchez, F.; Godin, T.; Hideur, A. Brillouin scattering-induced rogue waves in self-pulsing fiber lasers. Sci. Rep. 2017, 7, 45868. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Lu, P.; Bao, X. Compact single-end pumped Brillouin random fiber laser with enhanced distributed feedback. Opt. Lett. 2020, 45, 4236–4239. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulrhmann, S.; Alhasan, A.M.; Hakami, J. Influence of Optical Feedback Strength on Intensity Noise and Photon Number Probability Distribution of InGaAsP/InP Laser. Eng. Proc. 2025, 87, 5. https://doi.org/10.3390/engproc2025087005
Abdulrhmann S, Alhasan AM, Hakami J. Influence of Optical Feedback Strength on Intensity Noise and Photon Number Probability Distribution of InGaAsP/InP Laser. Engineering Proceedings. 2025; 87(1):5. https://doi.org/10.3390/engproc2025087005
Chicago/Turabian StyleAbdulrhmann, Salah, Abu Mohamed Alhasan, and Jabir Hakami. 2025. "Influence of Optical Feedback Strength on Intensity Noise and Photon Number Probability Distribution of InGaAsP/InP Laser" Engineering Proceedings 87, no. 1: 5. https://doi.org/10.3390/engproc2025087005
APA StyleAbdulrhmann, S., Alhasan, A. M., & Hakami, J. (2025). Influence of Optical Feedback Strength on Intensity Noise and Photon Number Probability Distribution of InGaAsP/InP Laser. Engineering Proceedings, 87(1), 5. https://doi.org/10.3390/engproc2025087005






