Modelling and Mechanical Characterization of a Metamaterial Inspired by the Spinodal Decomposition †
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Modeling: Cahn–Hilliard Equation
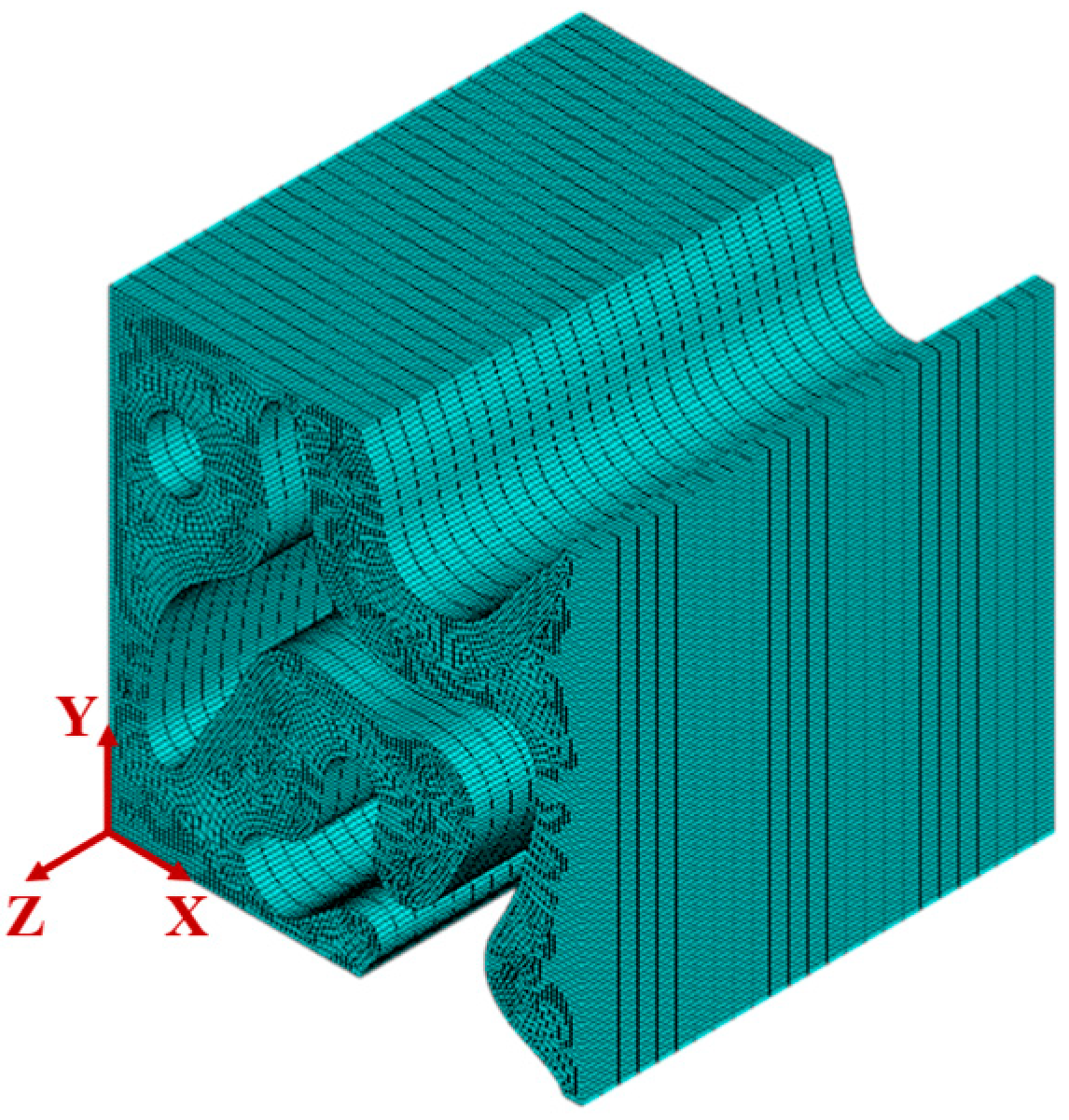
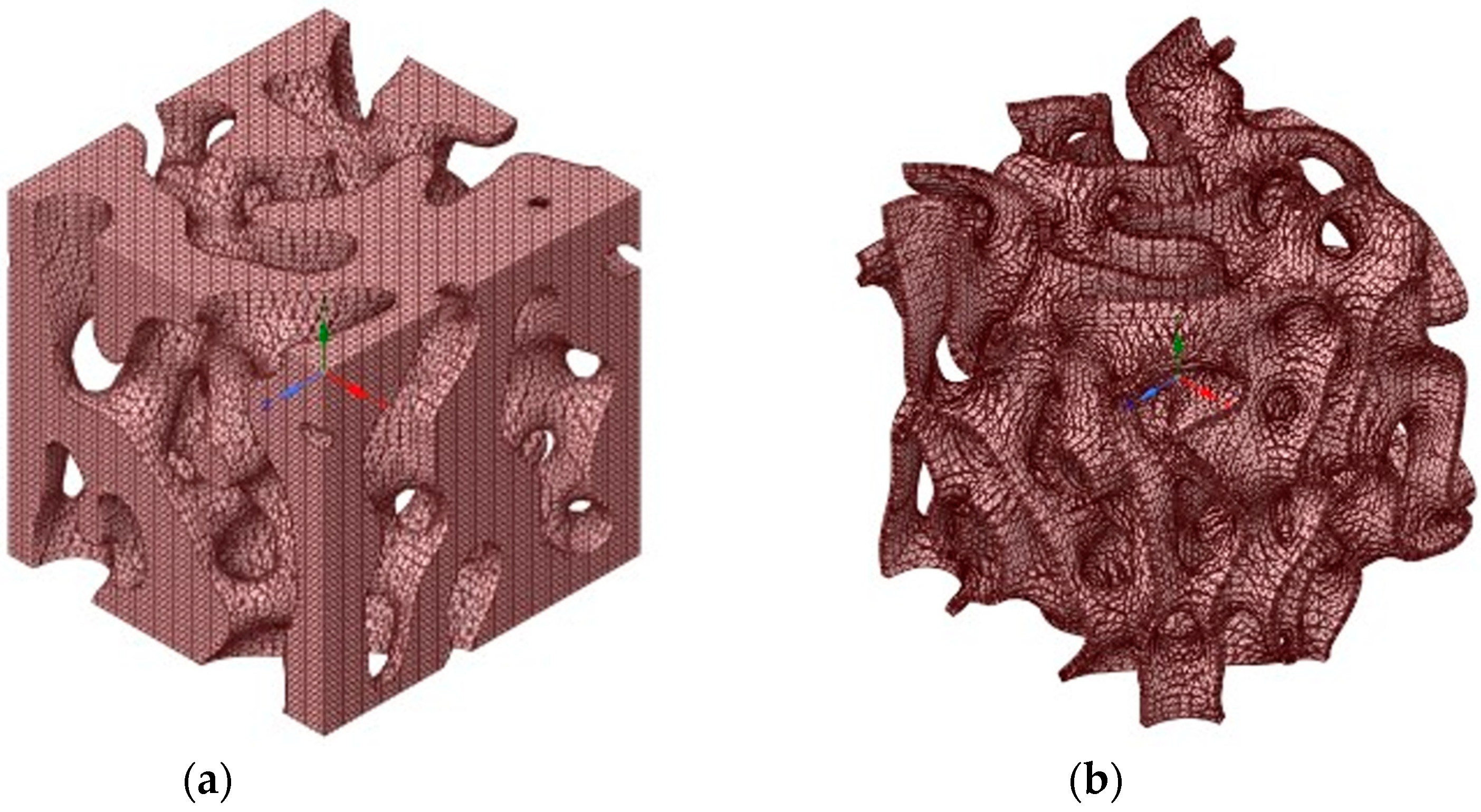
2.2. Computational Homogenization
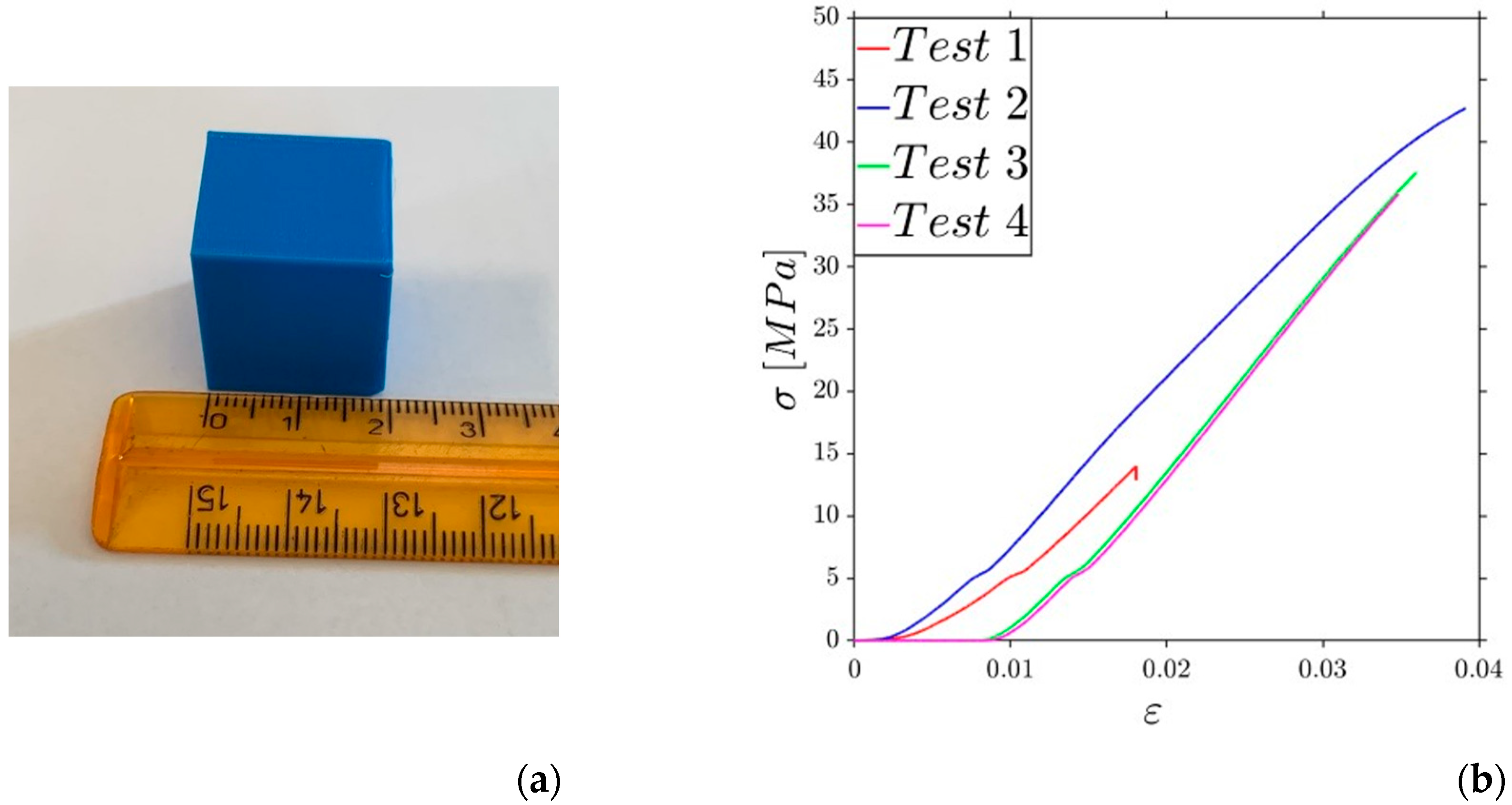
2.3. Experimental Testing
3. Results and Discussion
3.1. FE Homogenization Results
3.2. Experimental Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Askari, M.; Hutchins, D.A.; Thomas, P.J.; Astolfi, L.; Watson, R.L.; Abdi, M.; Ricci, M.; Laureti, S.; Nie, L.; Freear, S.; et al. Additive Manufacturing of Metamaterials: A Review. Addit. Manuf. 2020, 36, 101562. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical Meta-Materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X. Metamaterials: A New Frontier of Science and Technology. Chem. Soc. Rev. 2011, 40, 2494. [Google Scholar] [CrossRef]
- Bauer, J.; Meza, L.R.; Schaedler, T.A.; Schwaiger, R.; Zheng, X.; Valdevit, L. Nanolattices: An Emerging Class of Mechanical Metamaterials. Adv. Mater. 2017, 29, 1701850. [Google Scholar] [CrossRef] [PubMed]
- Valipour, A.; Kargozarfard, M.H.; Rakhshi, M.; Yaghootian, A.; Sedighi, H.M. Metamaterials and Their Applications: An Overview. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 2171–2210. [Google Scholar] [CrossRef]
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical Metamaterials and Beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef]
- Al Rifaie, M.; Abdulhadi, H.; Mian, A. Advances in Mechanical Metamaterials for Vibration Isolation: A Review. Adv. Mech. Eng. 2022, 14, 168781322210828. [Google Scholar] [CrossRef]
- Lu, C.; Hsieh, M.; Huang, Z.; Zhang, C.; Lin, Y.; Shen, Q.; Chen, F.; Zhang, L. Architectural Design and Additive Manufacturing of Mechanical Metamaterials: A Review. Engineering 2022, 17, 44–63. [Google Scholar] [CrossRef]
- Latture, R.M.; Rodriguez, R.X.; Holmes, L.R.; Zok, F.W. Effects of Nodal Fillets and External Boundaries on Compressive Response of an Octet Truss. Acta Mater. 2018, 149, 78–87. [Google Scholar] [CrossRef]
- Mateos, A.J.; Huang, W.; Zhang, Y.; Greer, J.R. Discrete-Continuum Duality of Architected Materials: Failure, Flaws, and Fracture. Adv. Funct. Mater. 2019, 29, 1806772. [Google Scholar] [CrossRef]
- Iandiorio, C.; Mattei, G.; Marotta, E.; Costanza, G.; Tata, M.E.; Salvini, P. The Beneficial Effect of a TPMS-Based Fillet Shape on the Mechanical Strength of Metal Cubic Lattice Structures. Materials 2024, 17, 1553. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rezgui, R.; Rowshan, R.; Du, H.; Fang, N.X.; Abu Al-Rub, R.K. Microarchitected Stretching-Dominated Mechanical Metamaterials with Minimal Surface Topologies. Adv. Eng. Mater. 2018, 20, 1800029. [Google Scholar] [CrossRef]
- Han, S.C.; Lee, J.W.; Kang, K. A New Type of Low Density Material: Shellular. Adv. Mater. 2015, 27, 5506–5511. [Google Scholar] [CrossRef] [PubMed]
- Bonatti, C.; Mohr, D. Smooth-Shell Metamaterials of Cubic Symmetry: Anisotropic Elasticity, Yield Strength and Specific Energy Absorption. Acta Mater. 2019, 164, 301–321. [Google Scholar] [CrossRef]
- Pini, V.; Ruz, J.J.; Kosaka, P.M.; Malvar, O.; Calleja, M.; Tamayo, J. How Two-Dimensional Bending Can Extraordinarily Stiffen Thin Sheets. Sci. Rep. 2016, 6, 29627. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and Failure Response of Imperfect Three-Dimensional Metallic Lattices: The Role of Geometric Defects Induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Symons, D.D.; Fleck, N.A. The Imperfection Sensitivity of Isotropic Two-Dimensional Elastic Lattices. J. Appl. Mech. 2008, 75, 051011. [Google Scholar] [CrossRef]
- Vidyasagar, A.; Krödel, S.; Kochmann, D.M. Microstructural Patterns with Tunable Mechanical Anisotropy Obtained by Simulating Anisotropic Spinodal Decomposition. Proc. R. Soc. A 2018, 474, 20180535. [Google Scholar] [CrossRef]
- Portela, C.M.; Vidyasagar, A.; Krödel, S.; Weissenbach, T.; Yee, D.W.; Greer, J.R.; Kochmann, D.M. Extreme Mechanical Resilience of Self-Assembled Nanolabyrinthine Materials. Proc. Natl. Acad. Sci. USA 2020, 117, 5686–5693. [Google Scholar] [CrossRef]
- Zheng, L.; Kumar, S.; Kochmann, D.M. Data-Driven Topology Optimization of Spinodoid Metamaterials with Seamlessly Tunable Anisotropy. Comput. Methods Appl. Mech. Eng. 2021, 383, 113894. [Google Scholar] [CrossRef]
- Kumar, S.; Tan, S.; Zheng, L.; Kochmann, D.M. Inverse-Designed Spinodoid Metamaterials. Npj Comput. Mater. 2020, 6, 73. [Google Scholar] [CrossRef]
- Hsieh, M.-T.; Endo, B.; Zhang, Y.; Bauer, J.; Valdevit, L. The Mechanical Response of Cellular Materials with Spinodal Topologies. J. Mech. Phys. Solids 2019, 125, 401–419. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W. Free Energy of a Nonuniform System. II. Thermodynamic Basis. J. Chem. Phys. 1959, 30, 1121–1124. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase Separation by Spinodal Decomposition in Isotropic Systems. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Sun, X.-Y.; Xu, G.-K.; Li, X.; Feng, X.-Q.; Gao, H. Mechanical Properties and Scaling Laws of Nanoporous Gold. J. Appl. Phys. 2013, 113, 023505. [Google Scholar] [CrossRef]
- Cahn, J.W. On Spinodal Decomposition in Cubic Crystals. Acta Metall. 1962, 10, 179–183. [Google Scholar] [CrossRef]
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Mandolesi, B.; Iandiorio, C.; Belardi, V.G.; Vivio, F. Spinodal decomposition-inspired metamaterial: Tailored homogenized elastic properties via the dimensionless Cahn-Hilliard equation. Eur. J. Mech.-A/Solids 2025, 112, 105615. [Google Scholar]
- Lynch, R.E. Fundamental Solutions of 9-Point Discrete Laplacians. Appl. Numer. Math. 1992, 10, 325–334. [Google Scholar]
- Hill, R. Elastic Properties of Reinforced Solids: Some Theoretical Principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Okereke, M.; Keates, S. Finite Element Applications; Springer Tracts in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-67124-6. [Google Scholar]
- Denisiewicz, A.; Kuczma, M.; Kula, K.; Socha, T. Influence of Boundary Conditions on Numerical Homogenization of High Performance Concrete. Materials 2021, 14, 1009. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, Y.; Ellyin, F. A Unified Periodical Boundary Conditions for Representative Volume Elements of Composites and Applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]
- Belardi, V.G.; Trupiano, S.; Fanelli, P.; Vivio, F. Overall Elastic Characterization of Equivalent FE Models for Aluminum Foams through Computational Homogenization Approach and Genetic Algorithm Optimization. Eur. J. Mech.-A/Solids 2024, 103, 105189. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Trupiano, S.; Vivio, F. Multiscale Analysis and Mechanical Characterization of Open-Cell Foams by Simplified FE Modeling. Eur. J. Mech.-A/Solids 2021, 89, 104291. [Google Scholar] [CrossRef]
- Nguyen, V.-D.; Béchet, E.; Geuzaine, C.; Noels, L. Imposing Periodic Boundary Condition on Arbitrary Meshes by Polynomial Interpolation. Comput. Mater. Sci. 2012, 55, 390–406. [Google Scholar] [CrossRef]
- Schneider, K.; Klusemann, B.; Bargmann, S. Fully Periodic RVEs for Technological Relevant Composites: Not Worth the Effort! J. Mech. Mater. Struct. 2017, 12, 471–484. [Google Scholar] [CrossRef]



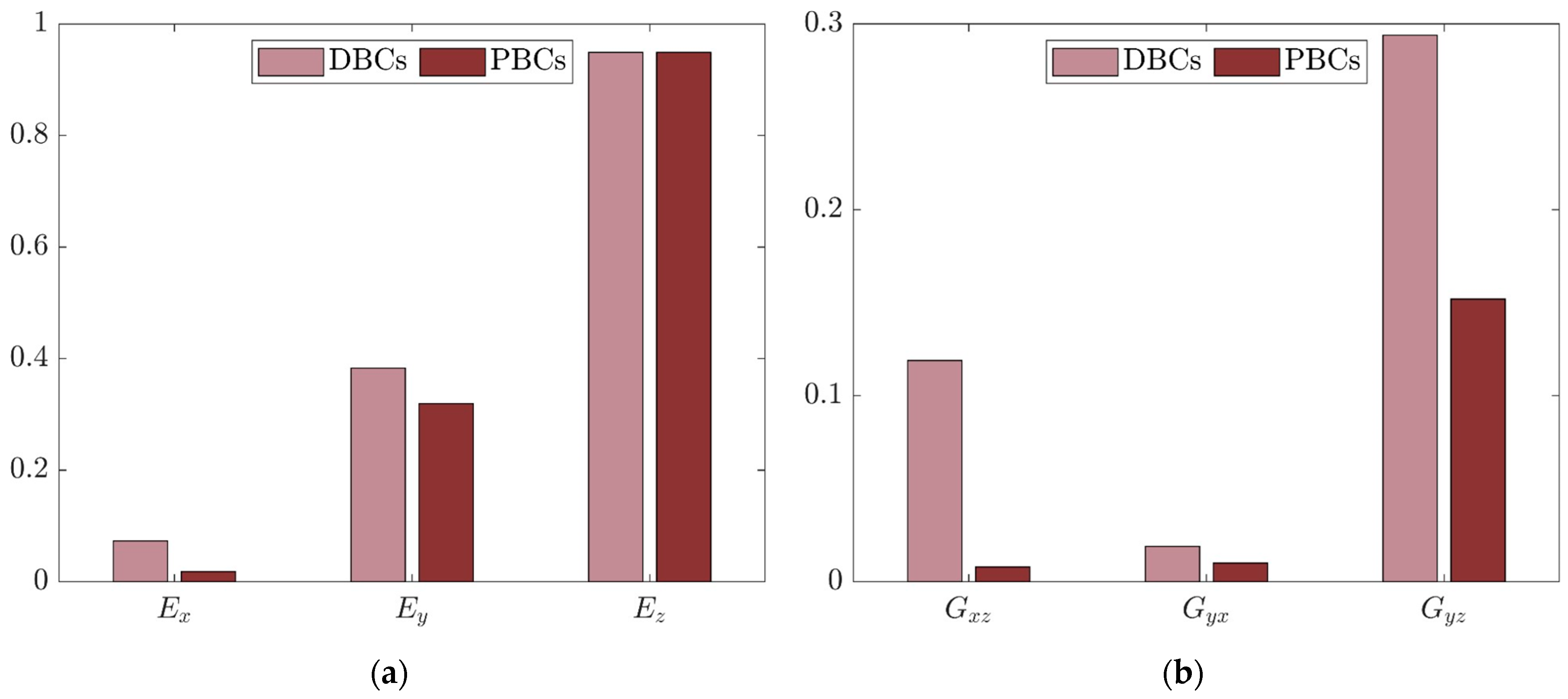
| DBCs | PBCs | |
|---|---|---|
| EX | 0.073 | 0.018 |
| EY | 0.383 | 0.319 |
| EZ | 0.949 | 0.949 |
| GXZ | 0.119 | 0.079 |
| GYX | 0.019 | 0.010 |
| GYZ | 0.294 | 0.162 |
| Test | FEM | Δ% | |
|---|---|---|---|
| EX | 0.020 | 0.018 | 9.55 |
| EY | 0.300 | 0.319 | 6.25 |
| EZ | 0.950 | 0.950 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandolesi, B.; Iandiorio, C.; Belardi, V.G.; Vivio, F. Modelling and Mechanical Characterization of a Metamaterial Inspired by the Spinodal Decomposition. Eng. Proc. 2025, 85, 40. https://doi.org/10.3390/engproc2025085040
Mandolesi B, Iandiorio C, Belardi VG, Vivio F. Modelling and Mechanical Characterization of a Metamaterial Inspired by the Spinodal Decomposition. Engineering Proceedings. 2025; 85(1):40. https://doi.org/10.3390/engproc2025085040
Chicago/Turabian StyleMandolesi, Barbara, Christian Iandiorio, Valerio G. Belardi, and Francesco Vivio. 2025. "Modelling and Mechanical Characterization of a Metamaterial Inspired by the Spinodal Decomposition" Engineering Proceedings 85, no. 1: 40. https://doi.org/10.3390/engproc2025085040
APA StyleMandolesi, B., Iandiorio, C., Belardi, V. G., & Vivio, F. (2025). Modelling and Mechanical Characterization of a Metamaterial Inspired by the Spinodal Decomposition. Engineering Proceedings, 85(1), 40. https://doi.org/10.3390/engproc2025085040







