Numerical Finite Element Modelling and Simplified Analytical Methodology for the Structural Analysis of Wound Rotors in Electric Motors ^†

Abstract

Wound rotor electric motors offer low production costs and environmental sustainability, making them preferable over rare-earth-based motors, particularly at low speeds. However, in automotive applications, the demand for higher specific powers and rotational speeds increases the structural challenges for wound rotors. While commercial Finite Element simulations integrate structural and electromagnetic needs, they could not immediately highlight the influence of single parameters on rotor stress. This paper introduces a simplified analytical methodology for the structural analysis of wound rotors, validated against Finite Element simulations, showing strong agreement. This approach is particularly useful during the early design stages for guiding preliminary geometry definitions.

1. Introduction

Wound rotor electric motors are characterized by low production costs and significant environmental sustainability, making them preferable to motors that use rare-earth materials, especially when low revving speeds are required [1,2,3]. In the automotive field, the constant need to increase specific power and, consequently, rotational speed creates a scenario that makes the use of wound rotors more challenging due to the inevitable increase in the stresses they are subjected to. 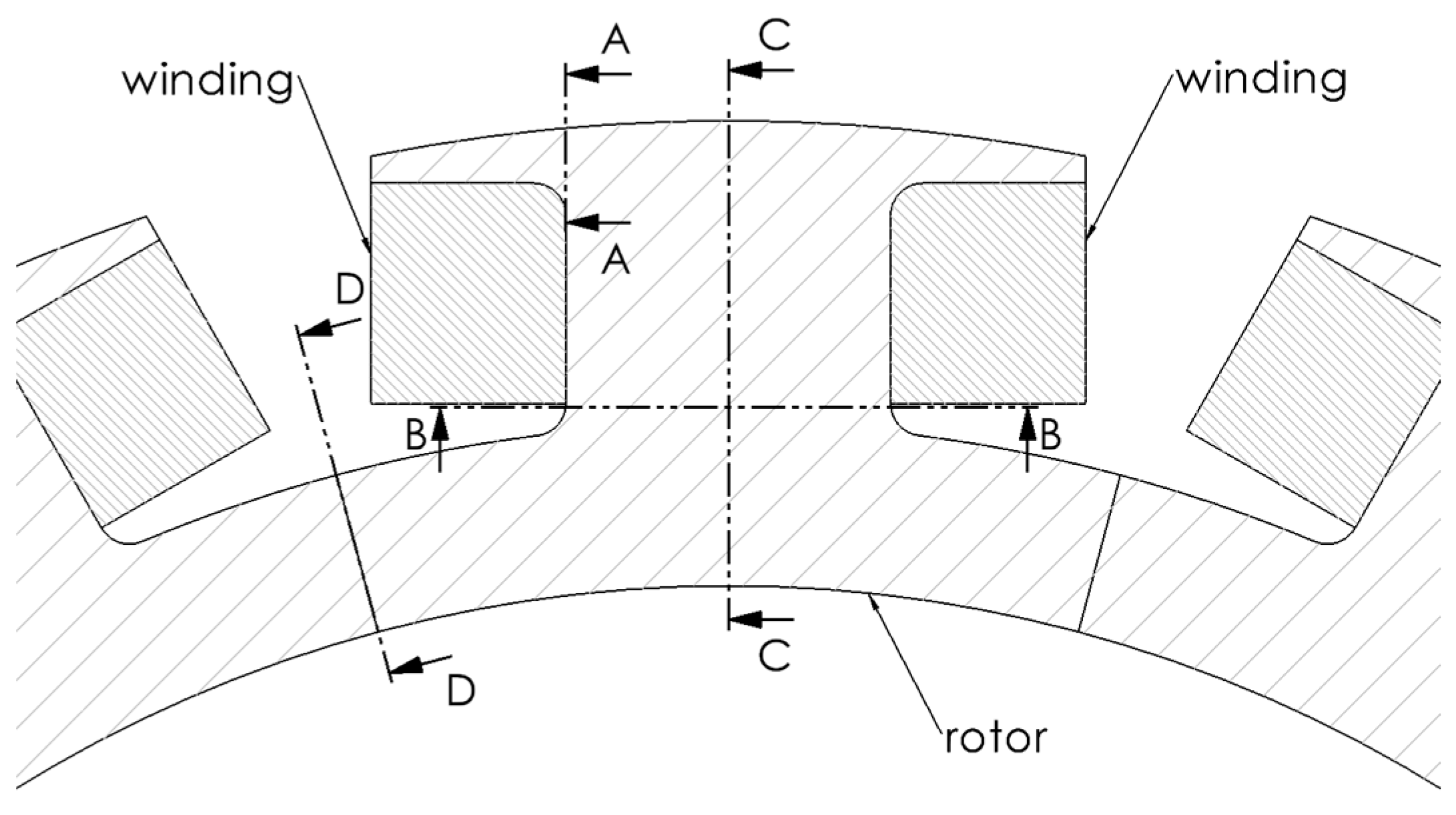Current commercial Finite Element software can integrate structural and electromagnetic requirements, but they do not clearly highlight the influence of the single design parameters on the stress state of the rotor [4,5]. In contrast, an analytical approach can explicitly show the dependencies of loads and stresses on design specifications and component geometries. This contribution proposes a simplified analytical methodology for the structural analysis of wound rotors in electric motors. This methodology is applied to the analysis of a prototype electric motor for heavy-duty vehicle traction. The results of the analytical calculations were also compared with Finite Element simulations, revealing a substantial correspondence between the two. Both plane stress and plane strain modelling are considered. The analysis includes a laminated steel sheet, the corresponding portion of the copper winding, and the influence of the shaft on which the rotor is mounted. The rotor body is modelled as a hollow cylinder with teeth modelled as T-shaped geometric structures radially arranged on the outer edge, around which the copper wires are wound. Four critical sections were identified to calculate the acting loading characteristics and the resulting stresses (see Figure 1).

This paper is organized as follows. In Part 2, the main characteristics of the motor under examination and the properties of the materials involved are described. Part 3 shows the simulation of the rotor performed with Finite Elements (FEs). These results will be used to compare and possibly validate the analytical calculations. In Part 4, section A-A is considered. This corresponds to the crossbar of the T-shape, which holds the copper winding and is mainly subjected to bending stress due to the centrifugal force generated by the mass of the winding and the crossbar itself. Part 5 examines section B-B, which corresponds to the base of the central body of the T-shape and is primarily subjected to normal stress due to centrifugal contributions, as well as the bending moment and shear load generated by the electromagnetic force. Part 6 focuses on Sections C-C and D-D, which are two radial sections of the back iron, located at the tooth and midway between two teeth, respectively. Finally, some conclusions end the manuscript.

2. The Motor Under Investigation

Table 1. Main parameters of the motor under investigation.

Parameter	Value	Unit
Number of poles	12	-
Revving speed	10,000	rpm
Torque	1400	Nm
External radius of the rotor	168	mm
External radius of the back iron	140	mm
Internal radius of the back iron	125	mm

collects the main characteristics of the motor under investigation.

Regarding the materials, a standard iron commonly used for electric motor rotors was selected. As for the windings, an equivalent homogeneous material was considered to account for the slot fill factor. However, it was crucial to accurately determine the density to properly calculate the centrifugal force generated, while the other characteristics were of marginal importance. These materials were considered linear elastic for both the analytical treatment and the numerical forecasts.

Table 2. Main parameters of the motor under investigation.

Parameter	Iron	Winding
Young’s modulus	185,000 MPa	60,107 MPa
Poisson’s ratio	0.3	0.3
Density	7650 kg/m3	5980 kg/m3

presents the material properties.

3. The Finite Element Analyses

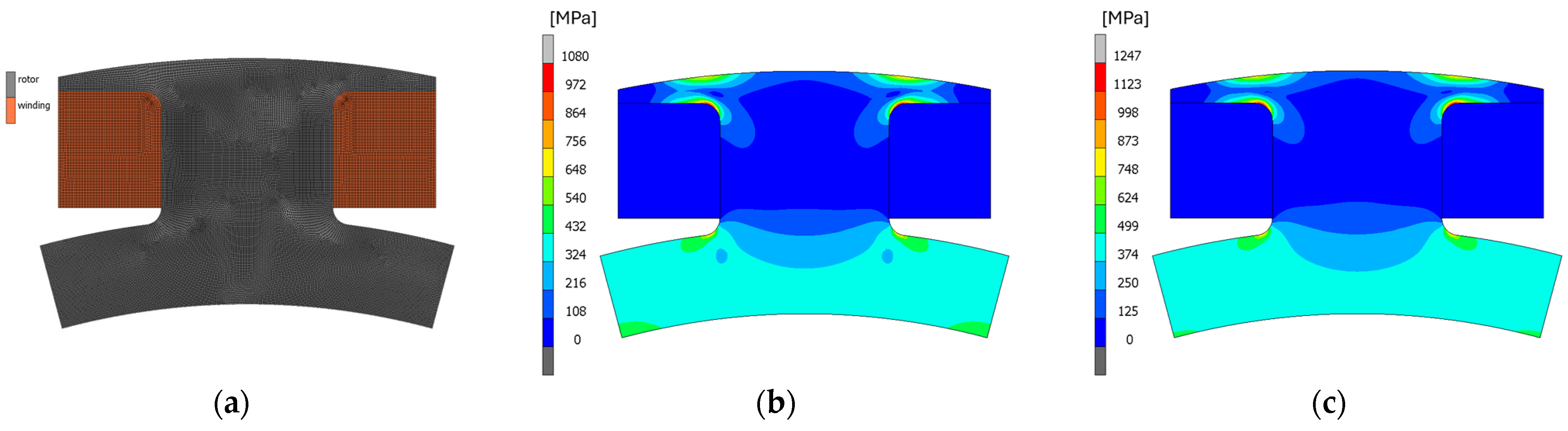
Figure 2a illustrates the FE model used in the analysis. The commercial software Marc2024 was employed. A twelfth of the rotor was considered, with appropriate periodicity conditions applied. Since the stress and strain in each layer are assumed to be unaffected by their axial location, a 2D FE model was implemented instead of a 3D one. This model includes a portion of the rotor and two sections of the winding. As a result of a sensitivity analysis, approximately 45,000 triangular and quadrilateral planar elements were used. Centripetal acceleration and a pressure of 6 MPa, to simulate the interference fit between the rotor and the shaft on the inner edge, were applied as boundary conditions. The torque generated by the motor was not included as it was deemed negligible, as later confirmed by analytical calculations.

The structural behaviour of the laminations was analyzed by considering two edge cases. The first case corresponds to laminations located in the middle of the active length of the motor, while the second case pertains to laminations at the axial periphery. Specifically, the first case is addressed by the plane strain hypothesis, while the second case is governed by the plane stress hypothesis. Figure 2b,c present the simulation results. Figure 2b shows the von Mises stresses for the plane strain case, while Figure 2c shows the von Mises stresses for the plane stress case. The two simulations yield slightly different results due to the presence of axial stress in the plane strain scenario. In the analytical discussion, both modelling strategies will be considered where applicable. It is also worth noting that the highest stresses are located on the laminate and with local maxima registered at the sections identified in Figure 1.

4. Section A-A: The Crossbar of the T-Shape

Figure 3a shows a detailed view of section A-A. The crossbar of the T-shape can be considered to be a cantilever beam fixed at the region identified by section A-A and subjected to the forces F_cw and F_cT, which are the centrifugal forces generated by the mass of the winding and the mass of the T-shape crossbar, respectively (see Figure 3b). The resultant force of the winding was calculated considering a uniform contact pressure at the interface with the crossbar.

The bending moment acting on section A-A can therefore be calculated as

$$M_{bA-A}=F_{cw}·d_{gxw}+F_{cT}·d_{gxT}$$

(1)

where d_gxw and d_gxT are the distances between the centre of gravity of the winding and the crossbar of the T-shape, respectively, from section A-A.

The bending stress can therefore be determined as

$${\sigma }_{{A-A}_x}={\displaystyle \frac{M_{bA-A}}{W_{A-A}}}·K_{tA-A}$$

(2)

where W_A−A is the section modulus of section A-A, and K_tA−A is the notch effect coefficient, here considered to be equal to 1.4 (see [6], page 193, Chart 3.7).

In the case of plane stress, σ_A−Ax coincides with the von Mises stress. However, in the case of plane strain, the stress arising in the axial direction must also be considered:

$${\sigma }_{{A-A}_z}={\sigma }_{{A-A}_x}·{\upsilon }_r$$

(3)

where ν_r is the Poisson’s ratio of the iron material used for the rotor.

Table 3. Section A-A, comparison of the results.

	FE	Analytical Calculation	Percentage Difference
Plane strain	1034 MPa	1155 MPa	12%
Plane stress	1208 MPa	1300 MPa	8%

shows the results of the analytical calculations and compares them with the numerical forecasts. Specifically, it focuses on the stress peaks located at the fillet. The analytical values are close to those obtained from the simulations, and the discrepancy can be ascribed to the uncertainty in the notch effect coefficient. The analytical formulas indicate that to reduce the stresses at section A-A, it is necessary to either decrease the centrifugal forces or minimize the overhang of the T-shape crossbar. While it may be challenging to reduce the masses and speeds to meet the motor’s performance targets, adjusting the geometry of the pole to limit the protrusion of the T-shape crossbar could offer a more feasible solution.

5. Section B-B: The Central Body of the T-Shape

Figure 4a shows a detailed view of section B-B. The central body of the T-shape can be considered to be a cantilever beam fixed at the region identified by section B-B and subjected to the forces F_cp and F_sw, which are, respectively, the tensile force generated by the mass of the winding and of the pole and the shear force calculated at the air gap necessary to create the required torque (see Figure 4b).

F_sw generates shear and bending moment on section B-B.

The shear stress can be calculated as

$${\tau }_{{B-B}_{max}}={\displaystyle \frac{F_{sw}}{A_{B-B}}}·{\displaystyle \frac{4}{3}}$$

(4)

where A_B−B is the cross-sectional area of section B-B, and F_sw is given by

$$F_{sw}={\displaystyle \frac{T_m}{n_p·r_{gw}}}$$

(5)

where T_m is the torque of the electric motor, n_p is the number of poles, and r_gw is the centroidal radius of the winding relative to the axis of rotation. For this specific motor, the calculations show that F_sw is quite low (808 N) due to the large size of the motor addressed in this case study. As a result, the shear stress is minimal (0.4 MPa) and can be considered negligible compared to the stresses caused by other factors.

Moving on to the bending stress generated on section B-B,

$${\sigma }_{{B-B}_{Mb}}={\displaystyle \frac{F_{sw}·d_{yr}}{W_{B-B}}}$$

(6)

where d_yr is the distance between the external profile of the rotor and section B-B and W_B−B is the section modulus of section B-B. In this case, the stress induced by the bending moment is also negligible (0.9 MPa).

However, the normal stress acting on section B-B cannot be neglected and is given by

$${\sigma }_{{B-B}_N}={\displaystyle \frac{F_{cp}}{A_{B-B}}}·K_{tB-B}$$

(7)

where F_cp is the centrifugal force generated by the pole, including the entire T-shape and winding mass, A_B-B is the cross-sectional area of the resisting section, and K_tB-B is the notch effect coefficient, here considered equal to 2.75 (see [6], page 184, Chart 3.1).

Table 4. Section B-B, comparison of the results.

	FE	Analytical Calculation	Percentage Difference
Plane strain	192 MPa	170 MPa	11%
Plane stress	217 MPa	192 MPa	11%

shows the results of the analytical calculations and compares them with the numerical forecasts. In this case, it appears that the resisting section is unnecessarily large, suggesting that the designer could consider increasing the space allocated for the winding, potentially reducing the rotor’s external dimensions. Once again, the analytical values are consistent with those from the simulations, with the discrepancy likely attributed to uncertainties in the notch effect coefficient. Additionally, the region of interest is close to the back iron, which experiences loading conditions more similar to a disc than a beam.

6. Sections C-C and D-D: The Back Iron

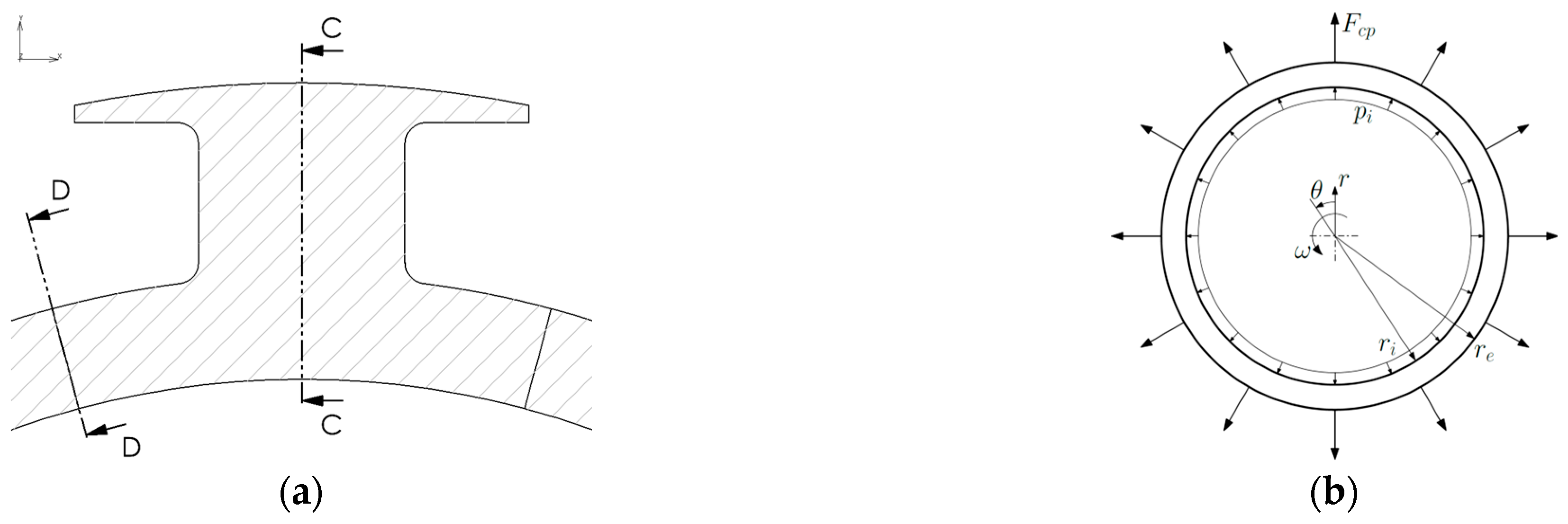
Figure 5a shows a detailed view of sections C-C and D-D. Considering the quasi-axisymmetric characteristic of the problem and with the aim of deriving a more robust and valid analytical model out of the applicability of the beam theory, in this case, a modelling approach based on the theory of elasticity is presented [7,8,9]. The analytical solution relies on a classical series solution in polar coordinates attributed to Michell [10]. This planar solution is particularly well suited for modelling discs subjected to different types of loading along their inner and outer edges, inspired by the methodology presented in [11].

The problem was modelled as a hollow disc subjected to concentrated loads (F_cp) at the outer edge, corresponding to the centrifugal force of each of the twelve rotor poles. The disc is also loaded by the centrifugal force generated by its own rotation (ω) and by the pressure at the inner edge due to the interference fit with the shaft (p_i), as shown in Figure 5b. To ensure the validity of the comparison with analytical calculations, the interference between the disc and the shaft was represented by applying a distributed pressure, as required by Mitchell’s theorem. While it is possible to simulate the interference more realistically, for example, by introducing a contact body representing the shaft with a proper interference fit, such an approach would impose displacement constraints, making it incompatible with the hypotheses of the theorem. This method was, therefore, avoided to preserve consistency with the analytical model.

The appropriate form of Airy’s stress function, Φ, expressed in polar coordinates in terms of a Fourier series, is (see [7], p. 119)

$$\begin{gathered} \mathsf{\Phi }\left(r,\theta \right)=C_{01}{r}^2+C_{03}\ln \left(r\right)+C_{04}\theta +C_{11}{r}^3\cos \left(\theta \right)+C_{12}r\theta \sin \left(\theta \right)+C_{14}{\displaystyle \frac{\cos \left(\theta \right)}{r}} \\ +\sum _{n=2}^{\mathrm{\infty }}\left(C_{n1}{r}^n+C_{n2}{r}^{n+2}+C_{n3}{r}^{-n}+C_{n4}{r}^{-n+2}\right)\mathrm{c}\mathrm{o}\mathrm{s}(n_p·n\theta ) \end{gathered}$$

(8)

where r is a general radius, and the origin of the angular variable θ is defined by Figure 5b. In addition, the stresses expressed in terms of Φ are (see [9], p. 66)

$${\sigma }_{rr}={\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^2\mathsf{\Phi }}{\partial {\theta }^2}}; {\sigma }_{\theta \theta }={\displaystyle \frac{{\partial }^2\mathsf{\Phi }}{\partial r^2}}; {\sigma }_{r\theta }={\displaystyle \frac{1}{r^2}}{\displaystyle \frac{\partial \mathsf{\Phi }}{\partial r}}-{\displaystyle \frac{1}{r}}{\displaystyle \frac{{\partial }^2\mathsf{\Phi }}{\partial \theta \partial \mathrm{r}}}$$

(9)

The boundary conditions to be applied to the disc are discussed in the following.

At the inner radius, radial and tangential stresses are defined as

$${\left.{\sigma }_{rr}\right|}_{r=r_i}={-p}_i; {\left.{\sigma }_{r\theta }\right|}_{r=r_i}=0;$$

(10)

where the pressure, p_i, mimics the interference fit with the shaft.

Twelve concentrated loads, F_cp, were applied at the outer radius, one for each pole. Specifically, these concentrated loads were applied using a trigonometric series corrected by the Lanczos factor [12] to smooth oscillations:

$${\left.{\sigma }_{rr}\right|}_{r=r_e}={\displaystyle \frac{F_{cp}{n}_p}{2\pi r_e}}\left(1+\sum _{n=1}^{\mathrm{N}}{\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\pi n}{N+1}\right)}{\left(\frac{\pi n}{N+1}\right)}}\mathrm{c}\mathrm{o}\mathrm{s}(n_p·n\theta )\right); {\left.{\sigma }_{r\theta }\right|}_{r=r_e}=0;$$

(11)

These boundary conditions must be applied to each harmonic, affecting the radial and tangential stresses along the outer radius of the disc as described by Equation (9) through the stress function Φ in Equation (8).

In addition, the centrifugal load related to the disc’s mass was incorporated using different methods for plane strain and plane stress conditions [13,14]. Specifically, for the plane strain condition, the approach considers the displacement u:

$$u=D_{1}r+{\displaystyle \frac{D_2}{r}}-{\displaystyle \frac{1}{8}}{\displaystyle \frac{(1+{\upsilon }_r)(1-2{\upsilon }_r)}{E(1-{\upsilon }_r)}}{\rho }_r{r}^3\omega$$

(12)

For the plane stress case, the following formulation was used:

$$u=D_{1}r+{\displaystyle \frac{D_2}{r}}-{\displaystyle \frac{1}{8}}{\displaystyle \frac{(1-{{\upsilon }_r}^2)}{E}}{\rho }_r{r}^3\omega$$

(13)

where ρ_r is the material density of the rotor. The stresses caused by the centrifugal loading (σ_rrc, σ_θθc and σ_rθc) were achieved and the constants D1 and D2 were then determined by applying the following boundary conditions:

$${\left.{\sigma }_{rrc}\right|}_{r=r_i}=0; {\left.{\sigma }_{r\theta c}\right|}_{r=r_i}=0; {\left.{\sigma }_{rrc}\right|}_{r=r_e}=0; {\left.{\sigma }_{r\theta c}\right|}_{r=r_e}=0;$$

(14)

Finally, the stresses generated by the interference fit pressure and the load on the outer radius were added to the stresses caused by the centripetal acceleration.

The analytical results were subsequently compared with the numerical forecasts.

Table 5. Section C-C, inner radius, comparison of the results.

	FE	Analytical Calculation	Percentage Difference
Plane strain	420 MPa	319 MPa	24%
Plane stress	470 MPa	355 MPa	24%

shows the von Mises stress results at the inner radius along section C-C.

Table 6. Section D-D, inner radius, comparison of the results.

	FE	Analytical Calculation	Percentage Difference
Plane strain	456 MPa	504 MPa	11%
Plane stress	510 MPa	563 MPa	10%

and

Table 7. Section D-D, outer radius, comparison of the results.

	FE	Analytical Calculation	Percentage Difference
Plane strain	364 MPa	299 MPa	18%
Plane stress	410 MPa	343 MPa	16%

compare the von Mises stress results at the inner and outer radius along section D-D, respectively.

The results demonstrate an alignment between the simplified analytical calculations and the simulation outcomes. However, there are noticeable limitations to accurately calculate the stresses in the back iron region, particularly where the T-shape is involved, i.e., section C-C. In this area, the load is not applied as a concentrated force but is instead distributed across the entire T-shape section. Moreover, the increased stiffness of the T-shape significantly alters the stress distribution compared to a simple disc.

7. Conclusions

This work has presented a simplified analytical methodology for calculating stresses in the most critical and defining areas of the geometry of wound rotors for electric motors. Four key regions were identified: the crossbar of the T-shape (section A-A), the body of the T-shape (section B-B), the back iron section beneath the T-shape (section C-C), and the back iron section between poles (section D-D). The analytical results were compared with FE analysis. For section A-A, the discrepancy in the results was never greater than 12%, while for section B-B, this difference was around 11%. Although the real loading conditions and the beam theory methodology leave little room for ambiguity, the presence of notches introduces some uncertainty in selecting the appropriate notch effect coefficient. For sections C-C and D-D, beam theory was abandoned in favour of elasticity theory. The proposed methodology resulted in discrepancies of 24% for section C-C and no more than 18% for section D-D. These results justify the applicability of the proposed method, especially in the early stages of designing a wound electric rotor, when evaluating different geometries in the early stage of the design process. In the future, this methodology could be improved by reconsidering the model of the back iron used in the theory of elasticity, where the highest errors were registered compared to Finite Element forecasts. In particular, a series of square waves could be applied to the outer radius of the back iron, instead of using a concentrated load, to better approximate the actual load distribution.