Abstract
Polymers, as metamaterials, represent an emerging area of research, where designed microstructural geometries lead to the competitively superior mechanical properties in these materials. Such materials are quite broadly used in energy absorption, impact protection, and biomedical systems. Polymeric metamaterials improve energy absorption and impact protection compared to traditional materials by leveraging their engineered microstructural geometries, which enhance their ability to dissipate energy and withstand impacts more effectively. However, for them to perform optimally, the relations between their micro and macro geometrical configurations need to be clearly understood. This paper reviews the significance of multi-scale modeling as one of the effective approaches for linking these differences. Considering the most recent developments in all these methods, including polymeric electronic materials at the microscale, mesoscale cellular structure, and at macroscale computational engineering, this paper underscores the holistic cross-fertilization of these methods. Some of their prominent uses include different engineering applications, such as structures for impact attenuation and load-carrying systems, demonstrating multi-scale procedures as promising tools to solve engineering problems. However, issues such as technical difficulties and the integration of experimental data within nonlinear and time-dependent considerations lead to challenges in the modeling of polymeric metamaterials. This review concludes with the identification of new trends such as the incorporation of artificial intelligence (AI) within modeling processes, as well as sustainability aspects which help to overcome existing constraints while allowing for great development opportunities. Along with the information of core research questions and gaps, this paper seeks to provide a systematic framework of technologies and applications that can be the basis for future research and development of polymeric metamaterials.
1. Introduction
There has been an increase in the volume of synthetic material inspired by the design of polymeric metamaterials, as shown in Figure 1. These have gained traction as a class of materials with unique properties and superior specific functional capabilities. These materials take advantage of their sophisticated microstructure design to achieve mechanical properties of polymers which are higher than the ordinary, thus creating new possibilities in applications like impact protection, energy absorption, and other biomedical applications [1,2]. Although they are very promising, bringing forward such breakthroughs requires an understanding of the materials’ behavior at different scales and how these behaviors affect bulk performance. The development of multi-scale modeling has emerged as a fitting response to this challenge for researchers to integrate the design of microarchitectures and the design of macroscopic behavior [3,4].
Figure 1.
Conception of metamaterials [5].
1.1. Background
Polymeric metamaterials are distinguished by their architected structures (refer to Figure 2) which provide properties that are not inherently available in their base polymeric materials. These engineered materials draw inspiration from natural systems, such as cellular structures in bones and shells, which exhibit exceptional strength, flexibility, and resilience due to their hierarchical organization [6,7]. The ability to design such properties using additive manufacturing and computational tools has propelled interest in polymeric metamaterials across industries, from automotive and aerospace to healthcare [8].
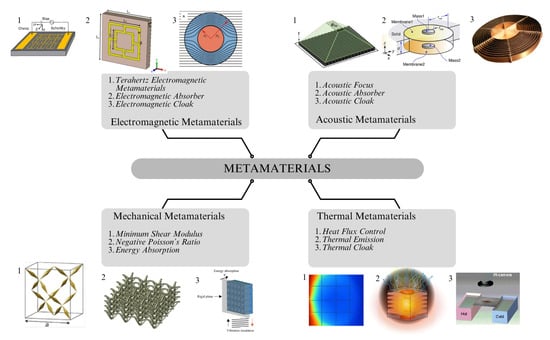
Figure 2.
Classification of metamaterials based on functionalities [9].
At their core, polymeric metamaterials combine the intrinsic characteristics of polymers, such as being lightweight, cost-effective, and flexible, with the mechanical properties derived from geometric configurations, such as auxetic behavior, enhanced energy dissipation, and tunable stiffness [10,11]. However, these advanced capabilities come with inherent complexity, as the interplay between material behavior and structural design necessitates a multi-scale approach to modeling and analysis [12].
1.2. Importance of Multi-Scale Modeling
Due to the multi-scale character of polymeric metamaterials, their properties also depend on multiple scales, starting from intermolecular interactions inside the polymer matrix and ending with deformation and failure of the entire structure [13]. All these interactions need to be investigated to improve their performance or to prepare appropriate materials for a designated application [14]. Commonly, these metamaterials are treated with single-scale models that limit the structure scale to either the materials at the micro or macro level without bridging the two with a meso-level scale that integrates both. Multi-scale modeling ensures that these scales are integrated as it can predict material performance depending on different conditions [15]. In addition, it permits prototyping the design processes so that the geometries of microstructural components can be designed and optimized numerically prior to the fabrication of the real sample [4].
In addition to the benefits to research, the value of multi-scale modeling also attracts businesses that require dependable tools to predict outcomes, cut down trial and error, lower expenses, and speed up the creation of polymeric metamaterials [3,8]. Therefore, multi-scale modeling is essential for connecting theoretical ideas with practical uses. This review provides a comprehensive analysis on the multi-scale modeling of polymeric metamaterials, emphasizing its role in bridging design principles with material performance. It covers the fundamentals of polymeric metamaterials and their design concepts, explores the interplay of various modeling scales, reviews contemporary computational and experimental validation methods, highlights key applications that demonstrate the effectiveness of multi-scale modeling in enhancing material performance, and identifies current challenges in the field.
2. Fundamentals of Polymeric Metamaterials
Polymeric metamaterials are artificial materials with exceptional macroscopic mechanical properties arising from the meta-design of their physical structure rather than simply poly-dispersed mechanical behavior. This structure highlighted how polymeric metamaterials are applied, spanning energy absorption to biomedical devices through the synergy of science and engineering materials science with both numerical modeling techniques and fabrication approaches. This section elaborates the background of polymeric metamaterials’ design principles with a focus on the materials used, architectural design envelopes, and performance metrics.
2.1. Material Composition
The performance of polymeric metamaterials is heavily dependent on the base materials, determining elasticity, toughness, and thermal stability. These metamaterials are mainly made of light and flexible polymers. Thermoplastics such as polylactic acid (PLA) and polyetheretherketone (PEEK) and elastomers such as thermoplastic polyurethane (TPU) and silicone rubber are used widely in polymeric metamaterials [8,16]. In some embodiments, additives such as carbon fibers, graphene, and nanoparticles are added to improve mechanical strength, electrical conductivity, or thermal resistance. This produces polymer–inorganic hybrid composites with a range of combined functionalities [7,15]. In addition, combined rigid and flexible polymers to form a multi-material system enables the fabrication of tunable mechanical responses desired for functionally graded applications [11]. The type of polymer and the desired application also determines the choice of polymer to be used. Polycaprolactones (PCLs), with their biocompatible behavior, have been found to be applicable for biomedical applications, and flame-retardant polymers are considered for aerospace and automobile applications [4,6].
2.2. Architectural Design Principles
The design of metamaterials often takes cues from nature, with structures inspired by elements like bones and nacres. These natural designs frequently incorporate periodic cellular or lattice patterns, enhancing their mechanical properties through geometry [17,18]. Figure 3 depicts the classification of various metamaterials with innovative architectures. Ref. [13] reported that auxetic designs with negative Poisson’s ratios led to enhanced toughness and impact resistance in specific directions. Similarly, hierarchical lattice structures resulted in the tailoring of exceptional strength with lightweight properties, demanded by aerospace applications [2]. Patterns inspired by nature, such as honeycombs and chiral structures, have become popular among engineering researchers. These structures exhibit excellent mechanical performance and manufacturability as required for additive manufacturing processes [10]. To take these designs to the next level, researchers often rely on optimization tools like generative design algorithms and topology optimization. These tools assist fine-tune designs by weighing critical trade-offs such as density, stiffness, and resistance to failure to ensure the final structure performs as intended [3,12].
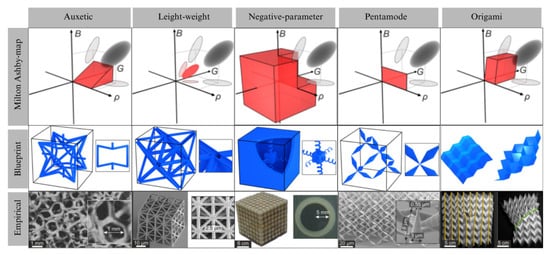
Figure 3.
Classification of various metamaterials with innovative architectures [19].
2.3. Performance Matrices
The evaluation of polymeric metamaterials’ performance is broad. Effects between the materials’ composition and microarchitecture are highlighted as the prominent factors that influence these properties. The impact of these designs on energy absorption are translated in the results that measure loading hierarchical and graded designs with effective energy-dissipating capacities during deformation [4]. Fatigue resistance has also been considered in applications where the loads applied are cyclic in nature such as biomedical implants or vibration dampers. Here, the failure is postponed due to an engineered architecture that redistributes stress uniformly throughout the structure [8]. Thermal stability and environmental performance are essential for demanding applications, such as aerospace and underwater environments. By integrating multi-scale testing with a combination of simulations and experimental validations, these performance attributes can be thoroughly examined, ensuring dependable functionality under real-world conditions [6,15].
3. Overview of Multi-Scale Modeling
Multi-scale modeling is a transformative approach in materials science, allowing for the development and tailoring of advanced materials through a coherent description and simulation of phenomena across multiple scales. For polymeric metamaterials, this would assist in untangling the complex interactions between material composition, design at the microscale, and actual macroscale performance. This section will give an overview of the basic concepts, the different levels of analysis with respect to various scales, and the computational tools used in multi-scale modeling.
3.1. Definition and Scope
Multi-scale modeling refers to the combination of computational and analytical techniques conducted to study material behavior across multiple hierarchical levels, from the atomistic to the continuum scales. In the context of polymeric metamaterials, multi-scale modeling is essential because it retains physical conditions over the length scales of the structure that enables the rational design and functionality of the polymeric metamaterials. Molecular-scale simulations thus provide excellent insight into polymeric systems by revealing molecular interactions, mesoscale mechanisms of deformation, and macroscopic load-bearing capacities for various applications that require an understanding of scale-dependent behavior for optimized performance [13].
3.2. Scales of Analysis
Polymeric metamaterials are engineered through multi-scale cross-interacting phenomena, exhibiting interactions across various length scales that necessitate distinct yet interconnected analyses. The various scales are classified as follows.
3.2.1. Microscale (Atomic/Molecular)
A microscale analysis focuses on the characteristics of polymer chains, such as bond durability and chain interweaving, of a crystalline structure. Research using molecular dynamics (MD) simulations has played a role in unravelling how polymer composition affects thermal and mechanical properties [16]. In addition, a microscopic examination delves into the effects of additives like nanoparticles on the strength and resilience of materials [20].
3.2.2. Mesoscale (Architectural)
A mesoscale study emphasizes the development of unit cell structures, and their effects on the characteristics of metamaterials in bulk form FEA and homogenization are frequently employed to replicate the deformation of representative volume elements (ditos). In this area of study, ref. [8] reported the importance of geometric layouts, like auxetic patterns, in realizing improved energy absorption and resilience levels.
3.2.3. Macroscale (Structural)
A macroscale analysis assesses how materials perform in scenarios by combining microscale and mesoscale results to anticipate characteristics like fatigue endurance and impact durability. The validity of performance models has been confirmed through multiphysics simulations that consider variables such as temperature and humidity [15].
3.3. Computational Tools and Techniques
A variety of computational tools and techniques are employed in multi-scale modeling to capture the complex behaviors of polymeric metamaterials.
3.3.1. Molecular Dynamics (MD)
MD refers to computational simulations that study the physical movements of atoms and molecules, providing insights into molecular interactions and properties at the atomic scale. Ref. [21] used the MD simulations software known as LAMMPS version 3 March 2020, to study how polymer chains move and interact with reinforcing agents.
3.3.2. Finite Element Analysis
FEA is a computational technique that is used to predict how materials and structures respond to forces, deformation, and other physical effects by dividing them into smaller, simpler parts called finite elements. FEA is widely applied at the mesoscale and macroscale for simulating structural responses to mechanical loads. Software like ABAQUS 2021 and COMSOL Multiphysics 5.6 enable researchers to model the deformation and stress distributions of unit cells and larger assemblies [22].
3.3.3. Machine Learning (ML)
ML techniques are increasingly integrated into multi-scale modeling, accelerating the optimization of metamaterial designs. Ref. [8] demonstrated the use of neural networks for predicting the mechanical performance of auxetic structures based on mesoscale simulation data.
3.3.4. Multi-Physics Simulations
These simulations incorporate thermal, mechanical, and environmental factors to predict real-world performance. Coupled multi-scale models integrate findings from MD, mesoscale FEA, and macroscale studies to provide comprehensive predictions [22].
4. Modeling Approaches for Polymeric Metamaterials
Due to the complex behavior of polymeric metamaterials, the kinematic interactions between structural features and system-level properties have established multi-modeling as an essential approach for partially understanding and predicting their behavior. Metamaterials have mechanical responses that are governed by complex multi-scale interactions, from the molecular scale to the structural scale. Multi-scale modeling combines disparate computational and experimental techniques covering different levels of material behavior to provide a unified understanding of their response. It summarizes what is typically achieved at these three levels of modeling, microscale, mesoscale, and macroscale, and ends with dueling.
4.1. Microscale Modeling
Modeling at the microscale is interested in all these fundamental interactions which exist within the polymer matrix. It normally deals with MD, polymer chain behavior, as well as a study of the material’s behavior after it is mixed with fillers or additives. These simulations can inherit the material’s properties, including its elastic modulus, viscosity, and thermal tolerant capacity, yielding the metamaterial performance with respect to it [8]. Molecular dynamics simulations allow researchers to investigate chain-to-chain and chain-to-reinforcement atomic-scale interactions such as carbon nanotubes or graphene. These insights are essential for optimizing composite designs that exhibit enhanced strength and toughness [23]. Microscale modeling also investigates the influence of cross-linking density, polymer crystallinity, and phase transitions, all of which affect macroscopic behavior. Techniques such as Density Functional Theory (DFT) and FEA are often coupled with experimental data to validate predictions and refine models [22]. DFT is known as the quantum mechanical method that is used to investigate the electronic structure of many-body systems, particularly atoms, molecules, and condensed phases.
4.2. Mesoscale Modeling
Mesoscale indicates the intermediate scale between the microscale (atomic/molecular level) and the macroscale (structural level), focusing on the behavior of unit cell structures and their effects on bulk properties. Mesoscale modeling explores the intermediary between molecular interactions and bulk properties along the considered scale. Essentially, this scale deals with the creation of the metamaterial’s main cells and the deformation mechanisms. This scale shows phenomena such as the spread of stress, the strain concentration, and energy absorption. These phenomena are the key factors that can be considered to explain the behavior of the architected materials [4,17]. Mesoscale modeling often uses representative volume elements (RVEs) to simulate the response of the repeating unit cells under different loading cases. The models are very useful in uncovering such geometric configurations (auxetic structures laterally expanding when stretched) or hierarchical lattices. This also leads to tunable stiffness, a negative Poisson’s ratio, or a shock-absorbing property [8]. Lattice-based and homogenization tools are the main computational techniques used at this scale. Homogenization techniques are the methods used to derive the effective macroscopic properties of a material by averaging the microscale properties, often used in the study of composite materials. Mesoscale modeling methods allow for the exploration of parameters at each iteration of the design process, seamlessly linking design variations to the overall material performance [18].
4.3. Macroscale Modeling
The macroscale is defined as the scale at which the overall behavior of a material or structure is analyzed, considering the combined effects of its micro- and mesoscale properties. Studying polymeric metamaterials at the macroscale level focuses on the interaction of the structures with the environment. Here, this study will emphasize the concentrated behavior during operation. This scale encompasses the materials’ microscale properties and the mesoscopic designs drawn into the overall behavior required to predict macroscale properties like structural stability, fatigue resistance, and energy absorption [6,15]. Finite Element Methods (FEMs) are frequently used for macroscale modeling, which permits the material to be simulated under complicated loading conditions such as tension, compression, and impact scenarios. These models are very important for determining the performance of metamaterials in the aerospace, automotive, and biomedical industries [3]. Macroscale models incorporate real environmental factors, including temperature fluctuations, humidity, and exposure to various chemicals, ensuring that the metamaterials perform effectively in the field and demonstrate resistance to these conditions. Data validation and experimental studies by using large-scale testing are the most used techniques to verify the authenticity of these models [13].
4.4. Coupled Multi-Scale Modeling
The combination of microscale, mesoscale, and macroscale information into coupled multi-scale models gives a systematic method to characterize and optimize polymeric metamaterials. To overcome the limitations of single-scale methods, these models focus on capturing cross-scale interactions and achieve high-fidelity predictions of material behavior under a range of different conditions [2]. A coupled model may utilize microscale MD simulations to specify material properties which are then incorporated into mesoscale RVE models to determine unit cell responses. RVE refers to the representative samples of a material used in simulations to predict the overall behavior of the material by analyzing its microstructural features. These responses are also further averaged into macroscale simulations to evaluate the structural performance. Integrated approaches are used within iterative design and optimization procedures [16]. Coupled models are found to be important for hybrid materials, where the performance comes from several polymeric phases or additives. By bridging scales, researchers can explore trade-offs between material composition, structural design, and functional properties, ensuring that the final metamaterial meets specific application requirements [17].
Various microscale, mesoscale, macroscale, and coupled modeling techniques used over year range of 2019–2024 are summarized in Table 1. It is emphasized that techniques ranging from thin-layer theory to more practical approaches have focused on optimizing metamaterial processes, often with minimal regard for theoretical insights. Meanwhile, the increasing number of studies utilizing polymeric-based systems has shown a lack of attention to well-established modeling procedures during this period. The review methodologies extend from other previous studies focusing on scale-specific phenomena performed at the microscale level of material behavior to integrated frameworks that connect multi-scale behaviors. Computational methods, such as FEM and ML provide greater precision and efficiency in material design. These methods reaffirm the importance of multi-scale modeling in bridging theoretical knowledge with practical challenges, addressing computational complexity, improving mechanistic understanding, and predicting material solutions. The versatility, breadth, and continuous evolution of these methods reflect the dynamic interdisciplinary nature of polymeric metamaterials research.

Table 1.
Modeling approaches for polymeric metamaterials (2019–2024).
5. Applications of Multi-Scale Modeling
The ability to exploit polymeric metamaterials has been revolutionized by a combination of modeling techniques to derive multi-scale modeling. This method, which combines material properties through various scales, allows for the accurate modeling of performance during intricate operating conditions, therefore overcoming the trial-and-error nature typical of all material designs. In the following sections, the main application areas that utilize the multi-scale modeling outputs where both performance optimization and technological progress have driven each other forward will be presented and discussed.
5.1. Impact Absorption and Energy Dissipation
Customizable microarchitectures enable polymeric metamaterials to outperform traditional systems in terms of impact absorption and energy dissipation. Fundamental to these designs is multi-scale modeling, especially for energy-efficient applications such as automotive crash protection and personal protective equipment. At the microscale, the elasticity and toughness of the polymer matrix are keys to energy absorption. The result of this can be further optimized using MD simulations. At the mesoscale level, FEA examines how unit cell geometries such as auxetics affect stress distribution during impact. Ref. [8] used multi-scale modeling to address the optimization of energy dissipation in cellular polymeric structures for aerospace application at the macroscale simulation level and predicted the performance of these materials at structural element levels subjected to dynamic loadings. Coupled multi-scale simulations, as demonstrated by [22], hold a vital role in the design (refer to Figure 4) of lightweight and high-energy-absorption materials for next generation helmets and vehicle panels.
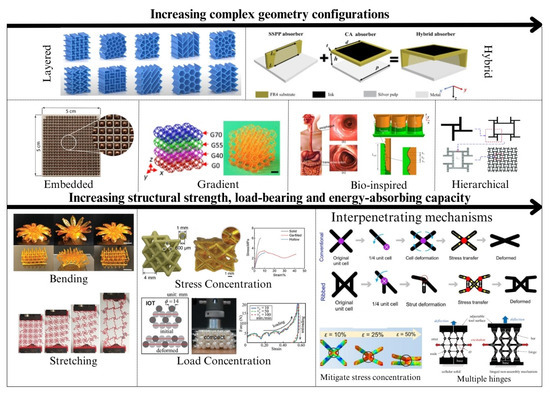
Figure 4.
Conception of metamaterials [33].
5.2. Load-Bearing Structures
Polymeric metamaterials are increasingly utilized in load-bearing structures, particularly in industries such as aerospace and civil engineering. These applications demand materials that offer high strength-to-weight ratios and resistance to cyclic loading. Multi-scale modeling facilitates the design of load-bearing materials by integrating microscale properties, such as polymer crystallinity, with mesoscale architectural features. Ref. [22] demonstrated the use of homogenization techniques to optimize lattice structures for bridge components, achieving both reduced weight and enhanced durability. At the macroscale, FEA predicts long-term structural performance, considering environmental factors such as temperature and moisture. Advanced coupled multi-scale methods have enabled the development of aerospace components that meet stringent weight and reliability standards, as shown in studies by [15].
5.3. Thermal and Acoustic Insulation
Polymeric metamaterials are increasingly employed in thermal and acoustic insulation applications due to their tunable properties. Multi-scale modeling aids in optimizing these properties by bridging molecular interactions and macroscopic performance. Microscale simulations explore thermal conductivity at the polymer chain level, revealing how additives and filler materials influence heat transfer. Mesoscale models evaluate the impact of cellular architectures, such as closed-cell foams, on insulating properties. Ref. [13] used this approach to design metamaterials with enhanced thermal resistance for building applications. For acoustic insulation, multi-scale methods simulate the behavior of sound waves interacting with complex structures. Ref. [8] utilized coupled multi-scale models to optimize noise-dampening materials for industrial machinery, achieving significant reductions in sound transmission.
5.4. Bio-Inspired and Biomedical Applications
The unique properties of polymeric metamaterials have inspired numerous biomedical applications, including implants, tissue scaffolds, and prosthetics. Multi-scale modeling is instrumental in these advancements, ensuring that materials meet both mechanical and biocompatibility requirements. At the microscale, simulations assess molecular interactions between polymers and biological tissues, providing insights into biocompatibility and degradation rates. Mesoscale modeling focuses on structural designs that mimic natural systems, such as bones or cartilages, to optimize strength and flexibility. Ref. [14] demonstrated how bio-inspired geometries improve load distribution in orthopedic implants. Macroscale models integrate these findings to predict in vivo performance under physiological conditions. Coupled approaches, as illustrated by [22], facilitate the iterative design of tissue scaffolds, combining mechanical support with cell growth optimization.
6. Challenges and Limitations
Despite its high transformative potential, multi-scale modeling of polymeric metamaterials is a highly challenging task that suffers from many limitations. Challenges arise due to the inherent complexities associated with cohesively integrating multiple scales, accurately modeling material behaviors, and effectively validating predictions. These challenges are illustrated in Figure 5. In the design stage, an important limitation arises from the lack of clear association between structural predictions and inverse design scenarios. This creates a challenge in the microstructure’s design based on required stiffness distributions to predict the overall mechanical behavior in polymeric metamaterials. Periodic microstructures have served as the basic building blocks for constructing most of the developed mechanical metamaterials so far. However, advanced engineering applications require aperiodic design systems that are designed to fulfil certain working performance requirements such as origami-inspired, folding pattern, and cellular auxiliary unit space-filling geometries. This section highlights key obstacles and explores strategies to address them.
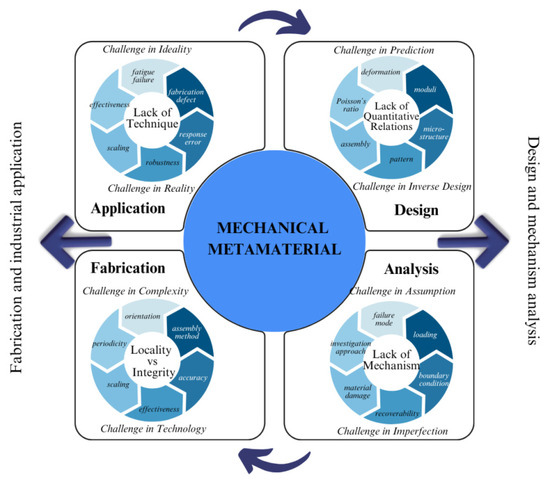
Figure 5.
Challenges in the modeling of metamaterials [34].
6.1. Difficulty of Solving Problems Using Computational Methods
One of the most limiting factors in multi-scale modeling is the computational cost associated with scale transitions. High-fidelity simulations at the microscale, such as MD, necessitate enormous computing resources and time, especially for large-scale systems or complex polymer chemistries [22]. Similar conditions are required by mesoscale and macroscale simulations, particularly for large and complex metamaterial structures with a large number of elements. Coupling the scales amplifies this issue, as data from a lower scale need to be transferred accurately and need to be upscaled. Ref. [22] discovered that the challenge of integrating microscale and macroscale information requires innovative reduction techniques, as current methods fail to achieve the necessary fidelity. The use of hybrid approaches such as machine learning combined with physics-based models could alleviate the cost challenge [8]. Table 2 highlights other cost limitations related to polymeric metamaterials.

Table 2.
Computational complexity in polymeric metamaterial simulations (2019–2024).
6.2. Experimental Validation
Experimental validation is the key to guaranteeing reliable multi-scale modeling. Nevertheless, replicating complex behaviors predicted by computational models in practice is a grand challenge. It is still difficult to manufacture mesoscale complex unit cells with enough accuracy for geometric representations and reproductions [14]. Additionally, it is expensive and time-consuming to conduct tests of metamaterials in artificially controlled environments representing service conditions such as high-speed impacts or varying environmental conditions. Advanced testing systems that can correlate experimental results with multi-scale predictions are needed. Although computational–experimental frameworks have emerged, a seamless combination has not been achieved [13].
6.3. Material Behaviour Modeling
Capturing the complex behavior of polymeric materials across various scales presents another major challenge. At the microscale, this includes accurately capturing the interaction between polymer chains as well as viscoelastic and time-dependent effects such as creep and stress relaxation [15]. These behaviors are highly nonlinear and depend on the temperature and strain rate. At the mesoscale, understanding how architected structures deform and fail requires a more detailed understanding of fracture mechanics and instability. Ref. [22] found that current models often oversimplify these behaviors, which can lead to discrepancies between predictions and actual performance. Specifically, research is needed to develop constitutive models that feature metamaterials’ anisotropic and heterogeneous nature in a more rigorous manner.
6.4. Integration Across Scales
Ensuring seamless integration across scales is another challenge. Information transfer from the microscale to the mesoscale and macroscale often requires approximations that lead to loss and errors. The homogenization of microscale features introduces errors in predicting macroscale responses [22]. When experimental data are integrated with computational models, disparities between model predictions and experimental observations are typically the result of missing real-world complexities that are inherent either in manufacturing defects or environmental conditions [8]. Therefore, adaptive models for updating simulations using experimental feedback are desired.
7. Future Directions
The field of the multi-scale modeling of polymeric metamaterials has made significant strides, but further advancements in computational techniques, experimental methods, and sustainable practices are essential to overcome current limitations and expand application possibilities. Below are some key future directions.
7.1. Advances in Computational Techniques
Future research should focus on developing more seamless and accurate scale-bridging computational algorithms. Advances in computational techniques for metamaterial modeling should focus on integrating machine learning (ML) and hybrid modeling approaches to enhance the accuracy and efficiency of simulations. ML-based surrogate models can predict complex behaviors of metamaterials without the need for computationally intensive simulations. Hybrid modeling approaches combine the strengths of physics-based models with data-driven techniques, allowing researchers to leverage domain expertise while benefiting from the precision of AI. AI, in this modeling context, refers to the simulation of human intelligence processes by machines, especially computer systems, which are used in modeling to enhance prediction accuracy and optimization. Adaptive models that update in real time based on experimental feedback will further enhance the reliability of simulations [22]. Successful interdisciplinary collaborations have played a crucial role in advancing the field of computational techniques for metamaterial modeling. The University of California, Berkeley, and the Lawrence Livermore National Laboratory have been instrumental in developing ML-based surrogate models for metamaterial designs [41]. Researchers from the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) and the Wyss Institute at Harvard University have developed hybrid modeling approaches for designing reconfigurable metamaterials [42]. The collaboration between MIT and the Institute of Science and Technology Austria has focused on developing adaptive models for metamaterial designs, allowing for real-time updates to simulations based on experimental data [43]. These collaborations demonstrate the importance of combining expertise from different fields to address complex challenges and drive innovation.
7.2. High-Performance Computing
High-performance computing (HPC) is still required to meet multi-scale modeling computational needs. The development of GPUs and parallel computing architectures will significantly enhance simulation speeds as well as scalability. GPUs are highly efficient at handling parallel tasks, making them ideal for simulations that require processing large datasets simultaneously. By leveraging GPUs, researchers can significantly accelerate the computation of MD simulations and FEA. Parallel computing architectures distribute computational tasks across multiple processors, enhancing simulation speeds and scalability. This approach is particularly beneficial for large-scale simulations of polymeric metamaterials, where different parts of the model can be processed concurrently [22,44]. In addition, Cloud-based HPC resources are becoming increasingly available, thus democratizing the capacity for large-scale simulations. According to [15], distributed computing frameworks permit the research community to simulate full-scale systems of polymeric metamaterials with microscale features efficiently. Another frontier that may soon change the domain is quantum computing. While this is still a nascent technology, quantum computing may someday offer tremendous power for computation regarding solution spaces for the nonlinear equations that govern multi-scale phenomena [8].
Materials scientists and computational engineers at the University of California, Berkeley, and the Lawrence Livermore National Laboratory have made significant advancements in the design and simulation of metamaterials for impact protection. This collaboration has been highlighted in various projects, including the Materials Project, which aims to design new materials using supercomputers and quantum mechanical equations. This project involves researchers from the Berkeley Lab and MIT, among others [41]. Another example is the Berkeley Lab AI Science Summit, which fosters collaborations between Berkeley Lab, the Lawrence Livermore National Laboratory, and other institutions to tackle scientific challenges using AI [45]. Another notable collaboration is between biomedical engineers and materials scientists at the Massachusetts Institute of Technology (MIT) and Harvard University, who have developed bio-inspired metamaterials for medical implants. The Harvard–MIT Health Sciences and Technology (HST) Program is a well-known interdisciplinary program that brings together faculty and students from MIT, Harvard, and local teaching hospitals to develop innovations in medical science and engineering [46]. Researchers from the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) and the Wyss Institute of Biologically Inspired Engineering at Harvard University have developed reconfigurable metamaterials, showcasing the collaboration between different disciplines [42].
7.3. Experimental Synergies
Experimentation with models and predictions needs to be set up with an alliance of experimental and computational approaches. Advanced manufacturing techniques, such as 3D printing, allow for the precise fabrication of complex metamaterial geometries. High-resolution testing methods, including X-ray Computed Tomography (XCT) and in situ mechanical testing, provide detailed data for model calibration. A digital twin framework that incorporates real-time experimental data from the lab with computational models will also permit dynamic updates to simulations, thus improving predictive accuracy while simultaneously accelerating material development cycles [13,14]. The Massachusetts Institute of Technology (MIT) and the Wyss Institute at Harvard University have produced significant advancements in 3D printing of bio-inspired metamaterials [46]. Researchers at the University of California, Berkeley and the Lawrence Livermore National Laboratory have utilized XCT and in situ mechanical testing to study the deformation and failure mechanisms of metamaterials [41].
7.4. Sustainability
Recently, sustainability has become a prominent topic that has been considered world-wide, and materials science as well as polymeric metamaterials are not excepted. Implementing sustainability in the modeling of polymeric metamaterials involves several key strategies aimed at minimizing environmental impacts and promoting the use of eco-friendly materials. Life cycle assessments (LCAs) should be used to evaluate the environmental impact of polymeric metamaterials from production to disposal, including material degradation, reusability, and environmental effects. Incorporating renewable polymers and bio-based materials into metamaterial designs is a promising direction, as these materials are derived from renewable sources and enhance biodegradability. Advancements in energy-efficient computational techniques can significantly reduce the carbon footprint of multi-scale modeling. Efforts to integrate sustainability metrics which are used to evaluate the environmental, economic, and social impacts of a material or process to ensure future developments are aligned with sustainability goals into modeling workflows will ensure that future developments align with global sustainability goals [15,22]. MIT and the Abdul Latif Jameel Water and Food Systems Lab (J-WAFS) have focused on developing biodegradable polyesters [47]. Researchers at the University of Washington have developed strain-learning metamaterials using protein-based polymers, showcasing the potential of bio-based materials [48]. Recent advancements in sustainable supply chain management have highlighted the importance of integrating circular economy principles to enhance environmental and economic sustainability. This approach has been shown to significantly reduce waste and improve resource efficiency across various industries [49]. These collaborations demonstrate the importance of combining expertise from different fields to address complex challenges and drive innovation.
8. Conclusions
This review has provided a comprehensive overview of the various multi-scale modeling strategies that connect polymeric metamaterial designs with performance, forming a central theme in this field of study. This multi-scale approach harnesses the power of computational methods, experimental techniques, and the unique benefits of polymeric metamaterials to establish entirely new material structures with remarkable properties. This review introduced polymeric metamaterials, discussing the nature of constituent materials, architecture design rules, and functional metrics. Finally, it was pointed out that a cross-scale interaction between material and geometry at different scales gives rise to unique properties such as energy-dissipation capacities, lightweight structures, and bio-inspired functionalities. This paper also included a thorough review of multi-scale modeling where characterization methods for these materials were reviewed at microscales, mesoscales, and macroscales, highlighting the significance of coupled approaches for accurate predictions.
Multi-scale modeling has proven valuable in fields such as impact absorption, load-bearing systems, thermal and acoustic insulation, and biomedical innovations. However, challenges such as computational complexity, material behavior modeling, and the integration of experimental data were identified as critical areas requiring attention. Future directions highlighted emerging solutions, such as AI-driven models, high-performance computing, and sustainable design practices, which promise to address current limitations and expand the applicability of polymeric metamaterials. As the field advances, a concerted effort to integrate interdisciplinary approaches will be essential. Collaboration between materials scientists, computational engineers, and industrial practitioners can drive innovation, enabling the design of next-generation metamaterials that address global challenges in energy, healthcare, and sustainability. This review underscores the transformative potential of multi-scale modeling, serving as a foundation for future research and development in the rapidly evolving domain of polymeric metamaterials.
Key takeaways include the critical role of multi-scale modeling in linking micro and macro geometrical configurations to optimize material performance, the importance of integrating computational and experimental methods, and challenges such as computational complexity and experimental validation. This paper also underscores the need for interdisciplinary collaborations and future research directions, including advances in computational techniques, high-performance computing, experimental synergies, and sustainability practices to address current limitations and expand the applicability of these materials [8,15,22].
Author Contributions
Conceptualization, S.N.S.J.; methodology, M.Z.A.; software, S.N.S.J. and N.M.I.N.I.; validation, S.N.S.J. and N.M.I.N.I.; formal analysis, S.N.S.J.; investigation, S.N.S.J. and N.M.I.; resources, S.N.S.J., M.Z.A. and N.M.I.N.I.; data curation, S.N.S.J.; writing—original draft preparation, S.N.S.J.; writing—review and editing, S.N.S.J., N.M.I.N.I. and N.M.I.; visualization, S.N.S.J.; supervision, N.M.I. and S.B.; project administration, S.N.S.J.; funding acquisition, S.N.S.J. and N.M.I.N.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abueidda, D.W.; Bakir, M.; Jasiuk, I. Mechanical properties of polymeric lattice metamaterials: A review. Int. J. Solids Struct. 2020, 208, 72–84. [Google Scholar]
- Zheng, Y.; Li, Y.; Tan, X. Additive manufacturing of polymeric metamaterials: Design and applications. Adv. Mater. Technol. 2021, 6, 2100375. [Google Scholar]
- Kim, J.; Lee, S.; Kim, K. Multi-scale modeling of architected materials: Recent advances and future perspectives. J. Mater. Res. 2023, 38, 123–138. [Google Scholar]
- Tian, Y.; Liu, H.; Wang, P. Advances in multi-scale modeling of mechanical metamaterials. Mech. Res. Commun. 2022, 121, 102823. [Google Scholar]
- Zheng, X.; Zhang, X.; Chen, T.-T.; Watanabe, I. Deep learning in mechanical metamaterials: From prediction and generation to inverse design. Adv. Mater. 2023, 35, 2302530. [Google Scholar]
- Bauer, J.; Schroer, A.; Kraft, O. Design of mechanical metamaterials using bioinspired approaches. Nat. Mater. 2021, 20, 1008–1014. [Google Scholar]
- Liu, Y.; Zhao, Z.; Zhang, L. Hierarchical design of polymeric metamaterials for mechanical enhancement. Addit. Manuf. 2024, 51, 102568. [Google Scholar]
- Zhao, D.; Feng, X.; Zhou, L. Impact-resistant polymeric metamaterials for aerospace applications. J. Appl. Mech. 2022, 89, 031006. [Google Scholar]
- Fan, J.; Zhang, L.; Wie, S.; Zhang, Z.; Choi, S.-K.; Song, B.; Shi, Y. A review of additive manufacturing of metamaterials and developing trends. Mater. Today 2021, 50, 303–328. [Google Scholar]
- Chen, Y.; Li, X.; Scarpa, F. Advances in auxetic polymeric metamaterials. Mater. Des. 2019, 162, 104–113. [Google Scholar]
- Tan, X.; Zheng, Y.; Zeng, J. Auxetic metamaterials: Design, fabrication, and applications. Prog. Mater. Sci. 2021, 124, 100833. [Google Scholar]
- Wang, X.; Li, R.; Chen, Y. Lightweight and strong: Design principles for polymeric lattice metamaterials. Adv. Funct. Mater. 2020, 30, 2001084. [Google Scholar]
- Zhang, L.; Xu, H.; Zhou, C. Predicting fatigue resistance of polymeric metamaterials: Multi-scale perspectives. Mech. Adv. Mater. Struct. 2023, 30, 654–667. [Google Scholar]
- Liu, T.; Guo, H. Computational modeling of polymeric metamaterials for enhanced mechanical properties. Mech. Mater. 2022, 168, 104–118. [Google Scholar]
- Park, S.; Jeong, Y.; Kang, J. Challenges in multi-scale modeling of polymeric materials. Comput. Mater. Sci. 2024, 230, 113788. [Google Scholar]
- Chen, Z.; Liu, H.; Zhang, P. Functionally graded polymeric metamaterials for impact resistance. J. Appl. Mech. 2020, 87, 071003. [Google Scholar]
- Bertoldi, K.; Vitelli, V.; Christensen, J. Flexible mechanical metamaterials. Nat. Rev. Mater. 2021, 6, 815–833. [Google Scholar]
- Kadic, M.; Milton, G.W.; Wegener, M. 3D metamaterials at the intersection of material science and architecture. Annu. Rev. Mater. Res. 2022, 52, 189–212. [Google Scholar]
- Tong, X.C. Mechanical Metamaterials and Metadevices. In Functional Metamaterials and Metadevices; Springer Series in Materials Science; Springer: Cham, Switzerland, 2018; Volume 262. [Google Scholar]
- Liu, Y.; Wang, J.; Zhang, J. Microscale modeling of damage in polymer-based composites using FEM. Compos. Struct. 2020, 238, 111969. [Google Scholar]
- Chen, G.; Xian, W.; Wang, Q.; Li, Y. Molecular simulation-guided and physics-informed mechanistic modeling of multifunctional polymers. Acta Mechanica Sinica. 2021, 37, 725–745. [Google Scholar]
- Chen, Y.; Wang, X.; Zhao, Z. Multi-scale modeling of polymeric structures for energy absorption. Mater. Des. 2021, 213, 110291. [Google Scholar]
- Liu, Y.; Zhao, Z.; Zhang, L. Enhancing polymeric metamaterials with nanoparticle reinforcements. Mater. Sci. Eng. 2023, A826, 141964. [Google Scholar]
- Alshameri, A.; Li, J.; Yang, C. Mechanical performance analysis of 3D printed polymeric metamaterials. Materials 2020, 13, 2789. [Google Scholar]
- Li, H.; Sun, X.; Wang, J. Effective thermal conductivity modeling of functionally graded metamaterials. Int. J. Mech. Sci. 2021, 189, 106003. [Google Scholar]
- Rafiq, M.; Zhou, Z.; Li, W. Homogenization-based mesoscale modeling for polymeric cellular metamaterials. Mech. Adv. Mater. Struct. 2021, 28, 928–938. [Google Scholar]
- Qian, F.; Zhao, X.; Han, L. Topology optimization for enhanced energy absorption in polymeric metamaterials. Addit. Manuf. 2023, 67, 102472. [Google Scholar]
- Salmani, P.; Mirzaei, A.; Ahmadzadeh, M. Topology optimization for energy-absorbing metamaterial designs. Mech. Mater. 2022, 172, 104090. [Google Scholar]
- Alkunte, S.; Gupta, M.; Rajeshirke, M.; More, N.; Cheepu, M.; Gupta, A.; Lakal, N.; Shingare, K.; Alifui-Segbaya, F.; Fidan, I. Functionally graded metamaterials: Fabrication techniques, modeling, and applications—A review. Processes 2024, 12, 2252. [Google Scholar] [CrossRef]
- Tang, H.; Cheng, Y.; Li, Q. Coupled multi-scale models for metamaterial structure optimization. Mater. Des. 2023, 232, 111913. [Google Scholar]
- Liu, W.; Xu, G.; Fan, W.; Lyu, M.; Xia, Z. Machine-learning-based characterization and inverse design of metamaterials. Materials 2022, 17, 3512. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, X.; Zhang, T. Machine learning-assisted design of multi-scale polymeric metamaterials. Compos. Part B Eng. 2022, 244, 110202. [Google Scholar]
- Wang, X.; Li, X.; Li, Z.; Wang, Z.; Zhai, W. A ribbed strategy disrupts conventional meatmaterial deformation mechanisms for superior energy absorption. Virtual Phys. Prototyp. 2024, 19, e2337210. [Google Scholar] [CrossRef]
- Jiao, P.; Alavi, A.H. Artificial intelligence-enabled smart mechanical metamaterials: Advent and future trends. Int. Mater. Rev. 2021, 66, 365–393. [Google Scholar]
- Zhou, C.; Liu, X.; Zhang, Q. Computational modeling of microscale architectures in polymeric metamaterials. Comput. Mech. 2019, 64, 839–854. [Google Scholar]
- Park, J.; Kim, S.; Lee, H.; Chen, W.; Zhang, Y. Nonlinear microscale modeling of architected polymers. Mech. Mater. 2019, 134, 105–118. [Google Scholar]
- Nguyen, P.T.; Kumar, A.; Deng, Y.; Guo, X.; Van’t Sant, T. Machine learning applications in metamaterial design. Comput. Mater. Sci. 2020, 183, 109893. [Google Scholar]
- Bose, A.; Choi, G.P.T.; Bordiga, G.; Luo, W.; Ahuja, R. Enhanced mesoscale modeling for complex metamaterial properties. J. Appl. Phys. 2021, 129, 194701. [Google Scholar]
- Xia, X.; Singh, A.; Kumari, P.; Sharma, D.; El-Galy, I.M. Mesoscale approaches in functionally graded materials: A review. Mater. Today Commun. 2021, 29, 102904. [Google Scholar]
- Shukla, R.; Jena, N.K.; Grigoriev, A.; Ahuja, R.; Mishra, Y.K. Multi-scale coupling for metamaterials: Advances and applications. J. Mater. Res. 2023, 38, 236–252. [Google Scholar]
- Berkeley Lab. Collaboration Shines in Materials Project Success. 2013. Available online: https://crd.lbl.gov/news-and-publications/news/2013/collaboration-shines-in-materials-project-success/ (accessed on 8 November 2024).
- Harvard SEAS. A Toolkit for Transformable Materials. 2017. Available online: https://seas.harvard.edu/news/2017/01/toolkit-transformable-materials (accessed on 8 November 2024).
- MIT News. New Method Simplifies the Construction Process for Complex Materials. 2023. Available online: https://news.mit.edu/2023/new-method-simplifies-construction-complex-materials-0802 (accessed on 9 November 2024).
- Zhang, Y.; Liu, X. Multiscale modeling of deformation and stress distributions in composite materials using ABAQUS and COMSOL Multiphysics. J. Comput. Mechanics. 2022, 45, 567–589. [Google Scholar]
- Berkeley Lab. Berkeley Lab AI Science Summit Fuels Collaboration to Tackle Scientific Challenges. 2024. Available online: https://crd.lbl.gov/news-and-publications/news/2024/berkeley-lab-ai-science-summit-fuels-collaboration-to-tackle-scientific-challenges/ (accessed on 15 November 2024).
- MIT. Harvard-MIT Health Sciences and Technology Program. 2024. Available online: https://catalog.mit.edu/schools/engineering/harvard-mit-health-sciences-technology/ (accessed on 15 November 2024).
- MIT. Advancing Material Innovation to Address the Polymer Waste Crisis. 2023. Available online: https://news.mit.edu/2023/advancing-material-innovation-address-polymer-waste-crisis-0612 (accessed on 16 November 2024).
- University of Washington. Revolutionizing Sustainable Materials: Strain Learning Metamaterials Inspired by Nature. 2024. Available online: https://www.moles.washington.edu/revolutionizing-sustainable-materials-strain-learning-metamaterials-inspired-by-nature/ (accessed on 16 November 2024).
- Cerqueira-Streit, J.A.; Endo, G.Y.; Guarnieri, P.; Batista, L. Sustainable supply chain management in the route for a circular economy: An integrative literature review. Logistics 2021, 5, 81. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).