Optimization of Dynamic Vibration Absorber on Ambulance Stretchers Using the Genetic Algorithm Method Based on ISO 2631 Standards ^†

Abstract

Ambulances play a crucial role in patient transportation and are often subjected to rapid accelerations, decelerations, and maneuvering. These dynamics can cause vibrations and instability, significantly impacting patient comfort and safety. This research aims to enhance patient comfort by implementing a dynamic vibration absorber (DVA) system on the stretcher of an ambulance. The DVA incorporates additional mass connected through a damping system to reduce pitching and bouncing effects, improving comfort levels according to ISO 2631 standards. The optimization of parameters such as the distance between the stretcher’s center of gravity and the DVA, spring constants, damping coefficients, and mass is carried out using a genetic algorithm (GA). By using a half-car model and sinusoidal road profiles, this study simulates and analyzes the impact of DVA on reducing vibrations. The results demonstrate a significant improvement in patient comfort and safety during ambulance transport.

1. Introduction

Ambulances play a crucial role in patient transportation and are often subjected to rapid accelerations, decelerations, and maneuvering. Ambulances need to face traffic conditions, road conditions, and obstacles [1,2]. Therefore, ambulances always experience vibrations and unstableness during trips to the hospital. Research has shown that ambulance vibrations and unstableness can negatively impact patient health and hinder paramedic care [3,4]. Patients transported in a recumbent position are more sensitive to vertical vibrations as compared to passengers in standing or seated positions [5]. Although few studies have been carried out analyzing the influence of stretcher stiffness on ride comfort for patients transported by ambulances [5,6], some works have shown that the use of a vibration attenuation system, such as a cabin suspension, can improve ride comfort [7,8,9]. In addition, vibration of the human body is most uncomfortable for sick or injured patients. Various approaches have been explored to mitigate these effects [10]. Research has implemented an artificial neural network controller for active shock absorbers, reducing patient mass vibrations by over 70% [11]. Another study used GAs to search for the optimal value of the damping coefficient and spring coefficient, resulting in a 96% decrease in acceleration on average for patients when driving at 70 km/h [12,13,14]. In other research using GAs to find the best suspension damping can reduce the acceleration of the driver’s seat. [15]. For ambulance stretcher design, GAs were used to determine optimal weighting coefficients for active suspension control, improving ride comfort and stability for patients [16]. The safety of patients’ bodies has been regulated by International Standard Organization (ISO) 2631 [17]. GAs were inspired by genetics from individuals with mutation processes in order to achieve the best genetic [18,19,20]. In this paper, DVA is proposed to reduce the vibration of stretchers in ambulances. The best effect is also supported by GA to find the best parameters, including DVA mass, spring coefficient, damping coefficient, and DVA position.

Building upon these advances, this paper focuses on developing and optimizing a DVA system to reduce vibrations affecting the ambulance stretcher. The integration of GAs into the DVA design process allows us to determine optimal parameters, including DVA mass, spring and damping coefficients, and the DVA’s position. This approach ensures the most effective vibration attenuation while maintaining system stability. By addressing both comfort and safety, this study aims to provide a significant contribution to ambulance design, ultimately improving patient outcomes during emergency transportation.

2. Methodology

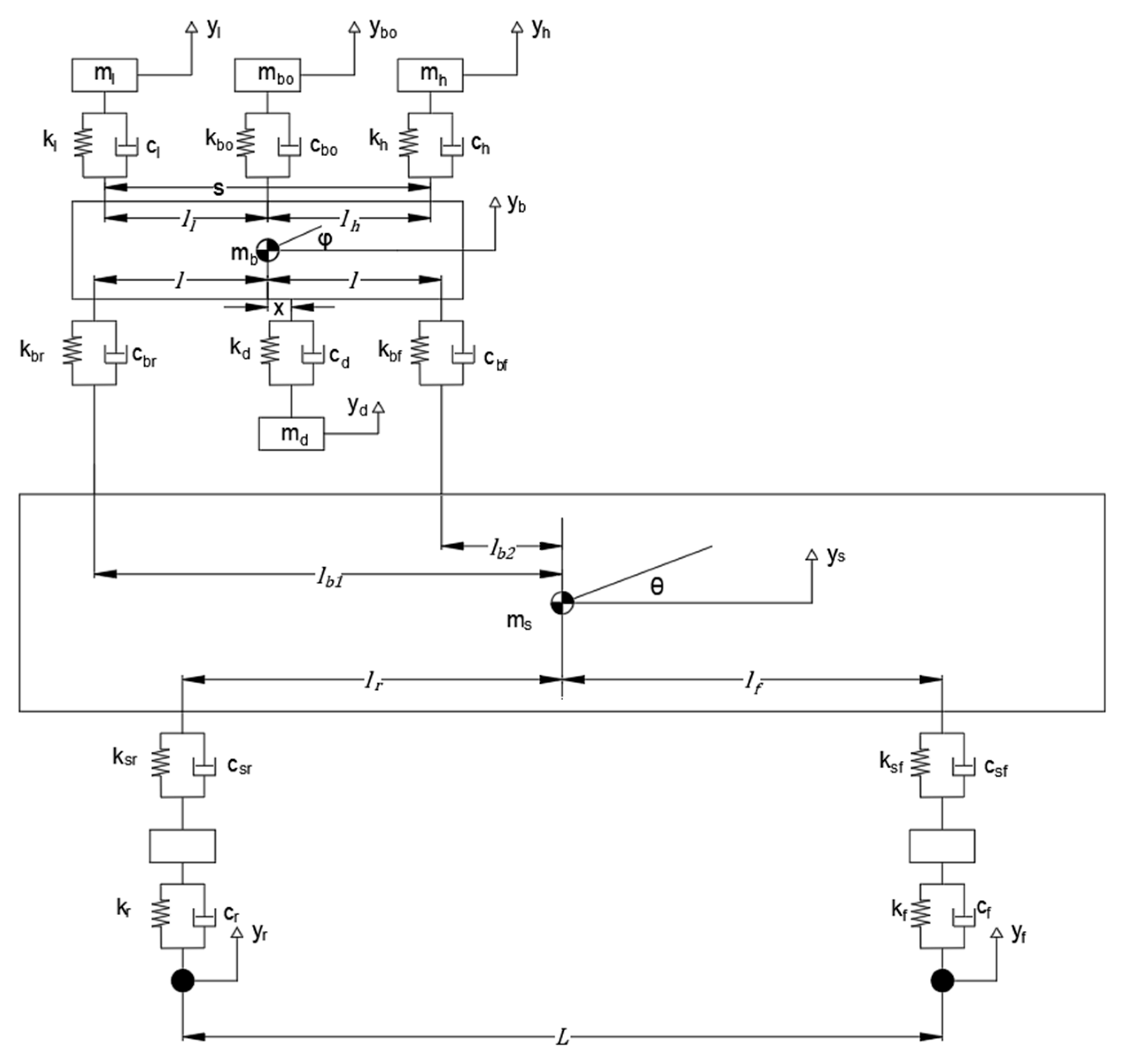
The first step in this study involved modeling the ambulance, stretcher, patient, and dynamic vibration absorber (DVA) using MATLAB Simulink. A half-car model was employed for the simulation, representing the dynamics of the system under investigation. This model incorporated a total of 10 degrees of freedom (DOFs) to comprehensively capture the vibrational behavior of the components. These DOFs were distributed as follows:

• Patient’s y-axis motion: 3 DOFs (head, body, and legs) to account for differential motion across the patient’s body.
• Stretcher’s y-axis motion: 1 DOF.
• DVA’s y-axis motion: 1 DOF.
• Ambulance’s y-axis motion: 1 DOF.
• Front tire’s y-axis motion: 1 DOF.
• Rear tire’s y-axis motion: 1 DOF.
• Pitch moment of the ambulance: 1 DOF to capture rotational effects.
• Pitch moment of the stretcher: 1 DOF to account for angular displacement.

The input for this model simulates road disturbances, such as a speed bump, represented as an impulse force. Figure 1 illustrates the proposed system scheme within the ambulance, showing the arrangement of components and their interactions.

For parameterization, the patient properties were adopted from the existing research [1], ensuring a realistic representation of human body dynamics. The ambulance specifications align with those of the Mercedes-Benz Sprinter 415 CDI, a commonly used vehicle in emergency medical services [17]. Key elements of the system, including the stretcher, DVA, and suspensions, are strategically modeled to mitigate vibrations and enhance ride comfort. Suspensions and the DVA are positioned beneath the stretcher to absorb and dissipate vibrations effectively, reducing the transmission of these forces to the patient. This comprehensive modeling approach serves as the foundation for subsequent simulation and optimization steps.

Figure 2 shows the full dynamic model of the system, illustrating the interaction between the stretcher, DVA, and vehicle suspension components. The model includes parameters such as masses $(m_d$), spring coefficients ($k_d$), damping coefficients ($c_d$), and the DVA position ($x$), which are critical for simulating and optimizing vibration control.

The next step involved optimizing the parameters of the DVA to determine the best combination that minimizes vibrations experienced by the patient. This optimization process utilizes a GA, a robust evolutionary computation technique, to efficiently search for the optimal parameters within specified ranges. The optimization focuses on four key parameters:

• Mass of the DVA, constrained within a range from 0 to 4 kg, which influences the absorber’s ability to counteract vibrations effectively.
• Spring coefficient, varying between 0 and 700,000 N/m, which determines the stiffness of the DVA and its capacity to absorb vibrational energy.
• Damping coefficient, ranging from 0 to 200,000 Ns/m, which regulates the dissipation of energy and ensures system stability during vibration suppression.
• DVA position, restricted to a range from −1.4 to 1.4 m, which impacts the dynamic response and efficiency of vibration absorption depending on its placement on the stretcher.

By systematically exploring these ranges, the GA identified the combination of parameters that minimize displacement and acceleration experienced by the patient, using the roulette method, random method, and tournament method to optimize the parameter.

The final step in this study involved conducting simulations using both the optimized parameters of the dynamic vibration absorber (DVA) and a baseline scenario without the DVA. This step is essential for evaluating the effectiveness of the proposed DVA system in mitigating vibrations. By comparing the displacement and acceleration experienced by the patient in both cases, we quantitatively assessed the improvement in ride comfort and stability provided by the DVA. Specifically, the simulations analyzed the vibration responses of the ambulance stretcher under typical operating conditions, including varying speeds and road profiles. The results highlight the reduction in vibrations and accelerations achieved with the DVA, validating the optimization process and demonstrating the potential of the system to enhance patient safety and comfort during emergency transport.

3. Result and Discussion

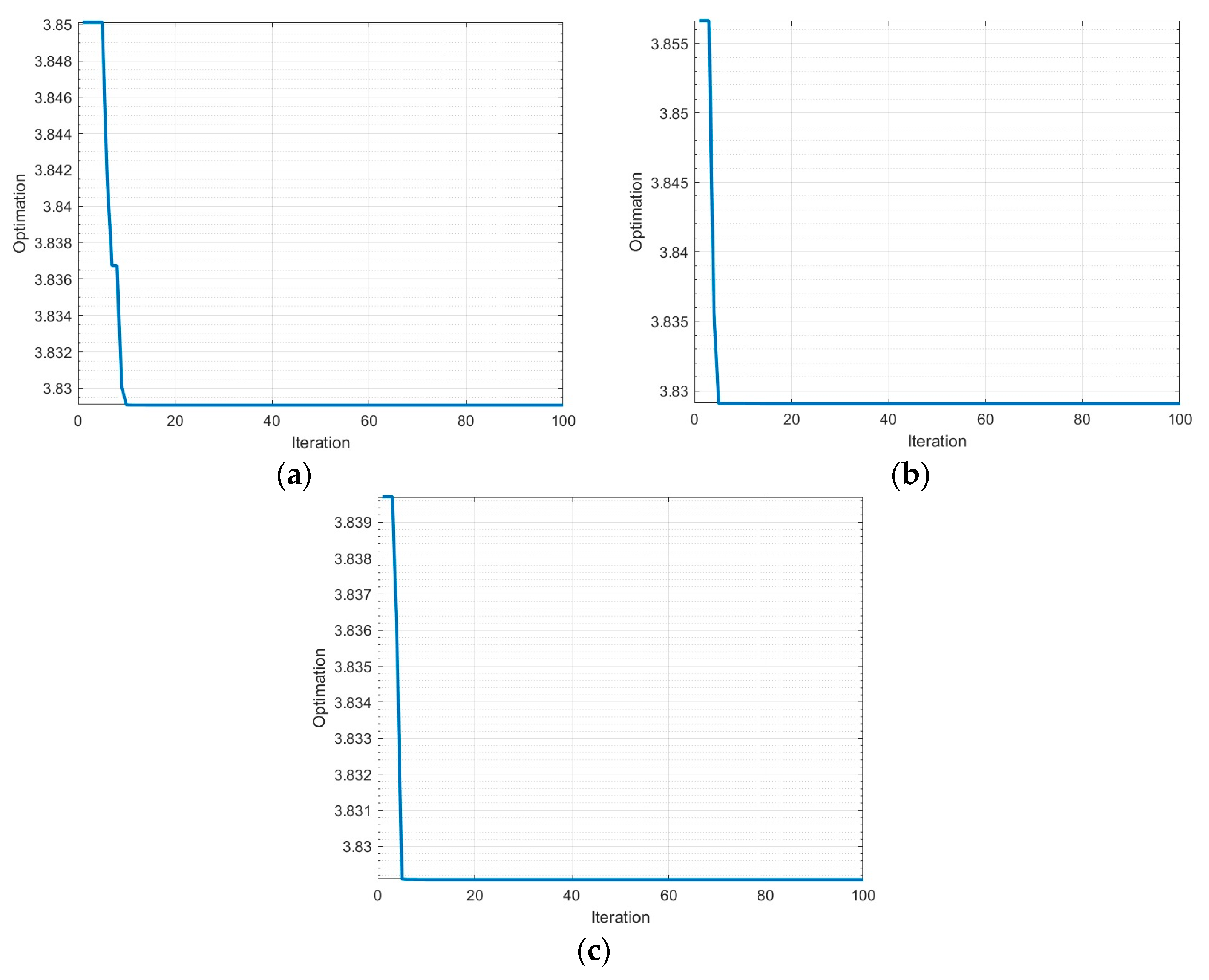
In this initial test, we searched for the most optimal parameters of DVA mass, spring coefficient, damping coefficient, and DVA position. The simulation was conducted with MATLAB Simulink and the GA code was built to find the most optimal parameters. Figure 3 shows that the quickest methods to find the most optimal parameters are the tournament method and the random method, with which the best parameter can be calculated within five iterations. However, the calculation needs 10 iterations in the roulette wheel (RW) method in order to find the best parameter.

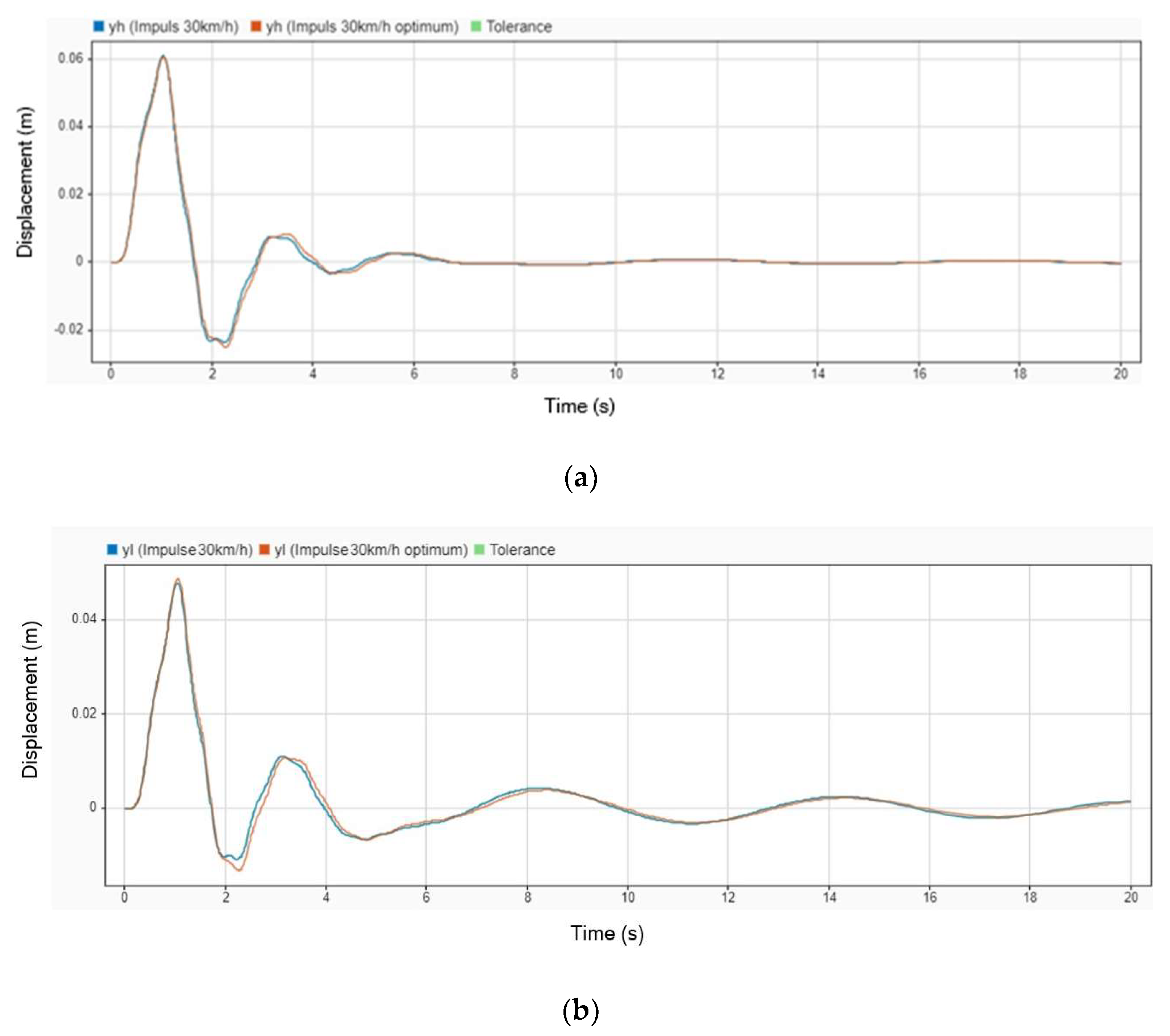
In the subsequent simulation, the parameters outlined in

Table 1. Best parameter from RW method, tournament method, and random method.

Method	DVA Mass (kg)	Spring Coefficient (N/m)	Damping Coefficient (Ns/m)	DVA Position (m)
Random	4	700,000	200,000	1.4
Tournament	4	700,000	200,000	1.4
RW	4	700,000	200,000	1.4

were applied, and an impulse road input was introduced while the vehicle traveled at a velocity of 30 km/h. The results, depicted in Figure 4, compare the vibration response of a stretcher equipped with a DVA against one without it. The blue line represents the vibration profile when no DVA is installed on the stretcher, while the orange line illustrates the enhanced stability and reduced vibrations achieved when a DVA is utilized. This highlights the effectiveness of DVA in mitigating the transmission of road-induced vibrations, thereby improving patient comfort and safety during transit.

Figure 5 demonstrates the effectiveness of using a DVA in reducing vibrations at various parts of the patient’s body during transit. The peak amplitude of displacement at the head, body, and legs decreased by 5.00%, 4.74%, and 4.78%, respectively, when the DVA was employed. The results indicate that the patient’s head and body reached a steady state within 7 s, signifying effective vibration damping in these areas. However, the patient’s legs exhibited prolonged oscillations, persisting even after 20 s, suggesting a need for further refinement in the DVA’s design or positioning to ensure consistent damping across all body regions. These findings underscore the potential of DVA technology to enhance patient comfort and stability during ambulance transport.

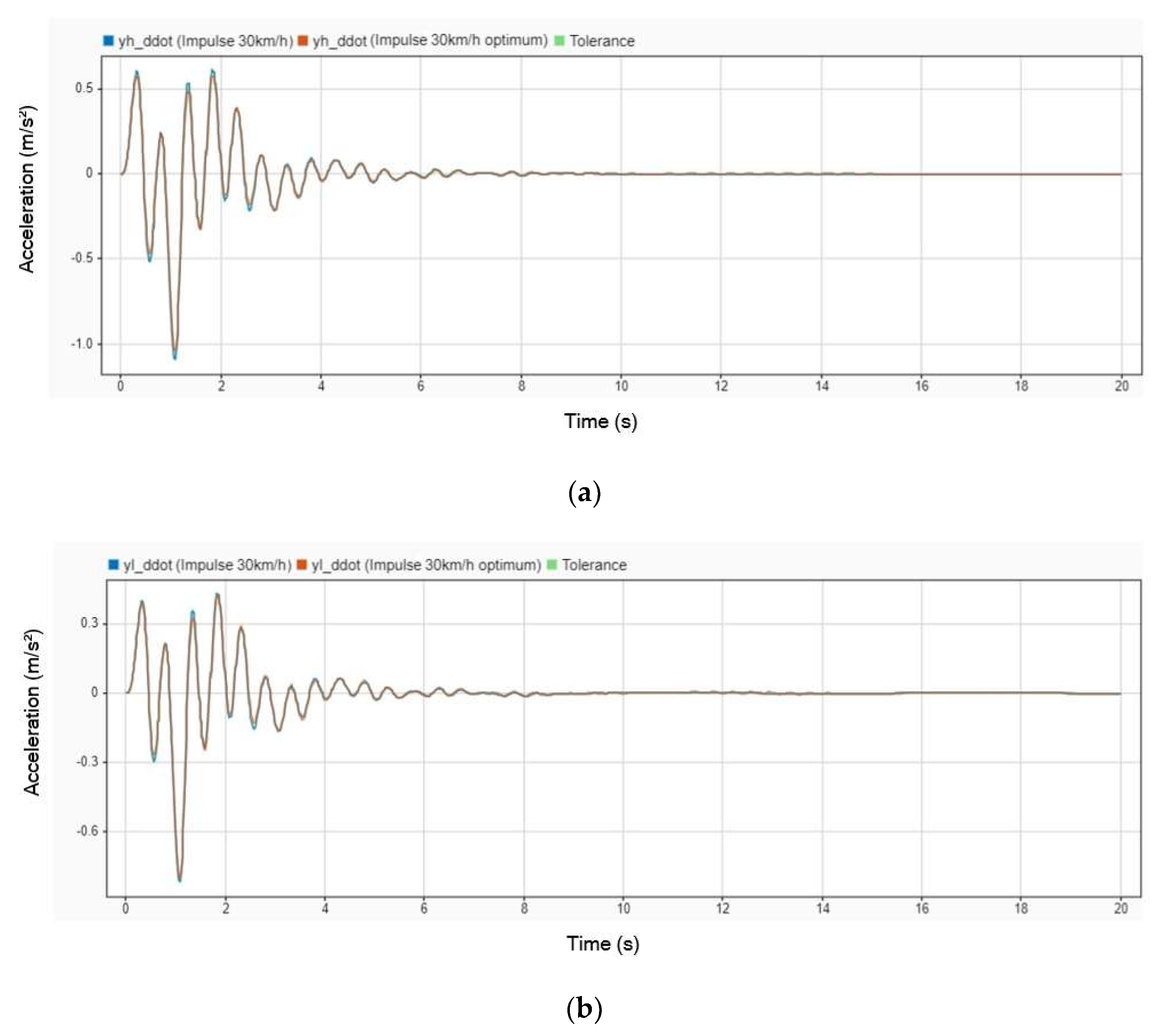
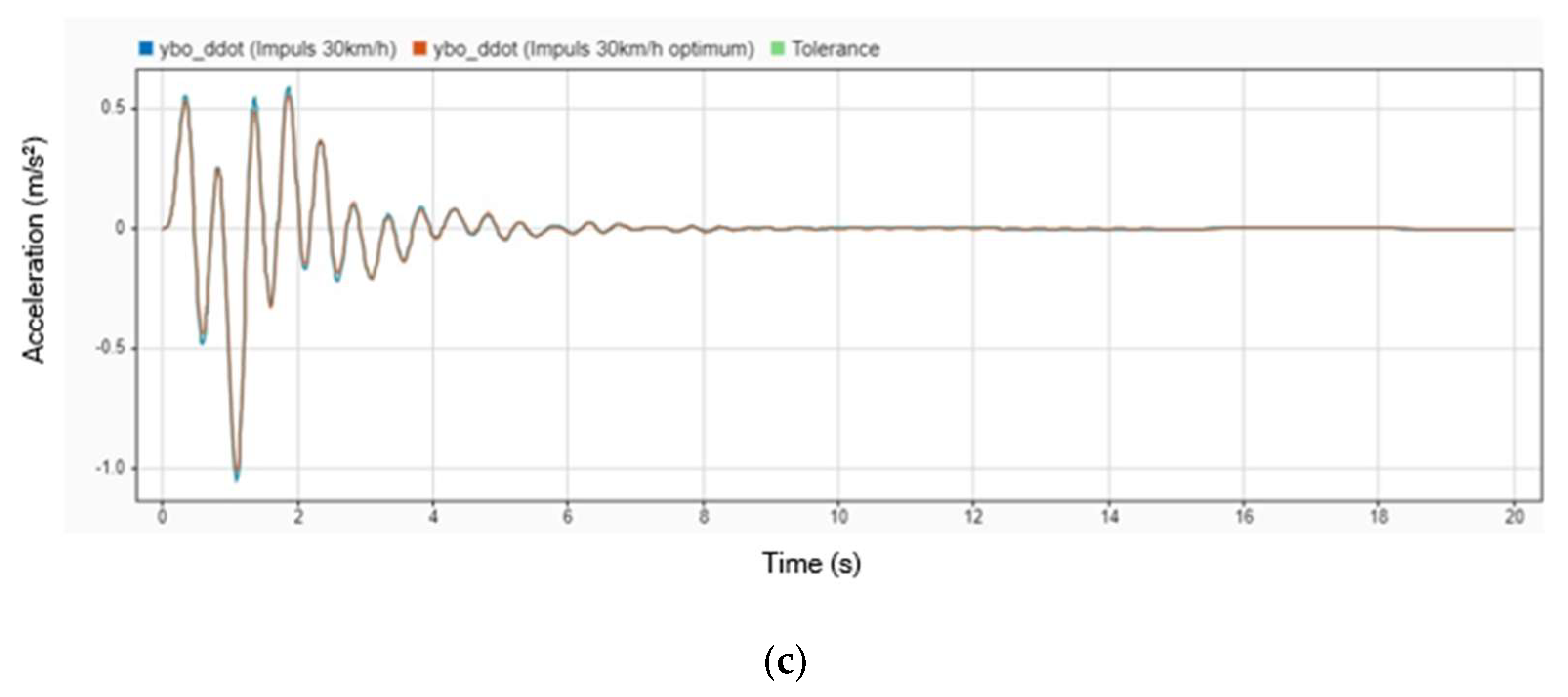
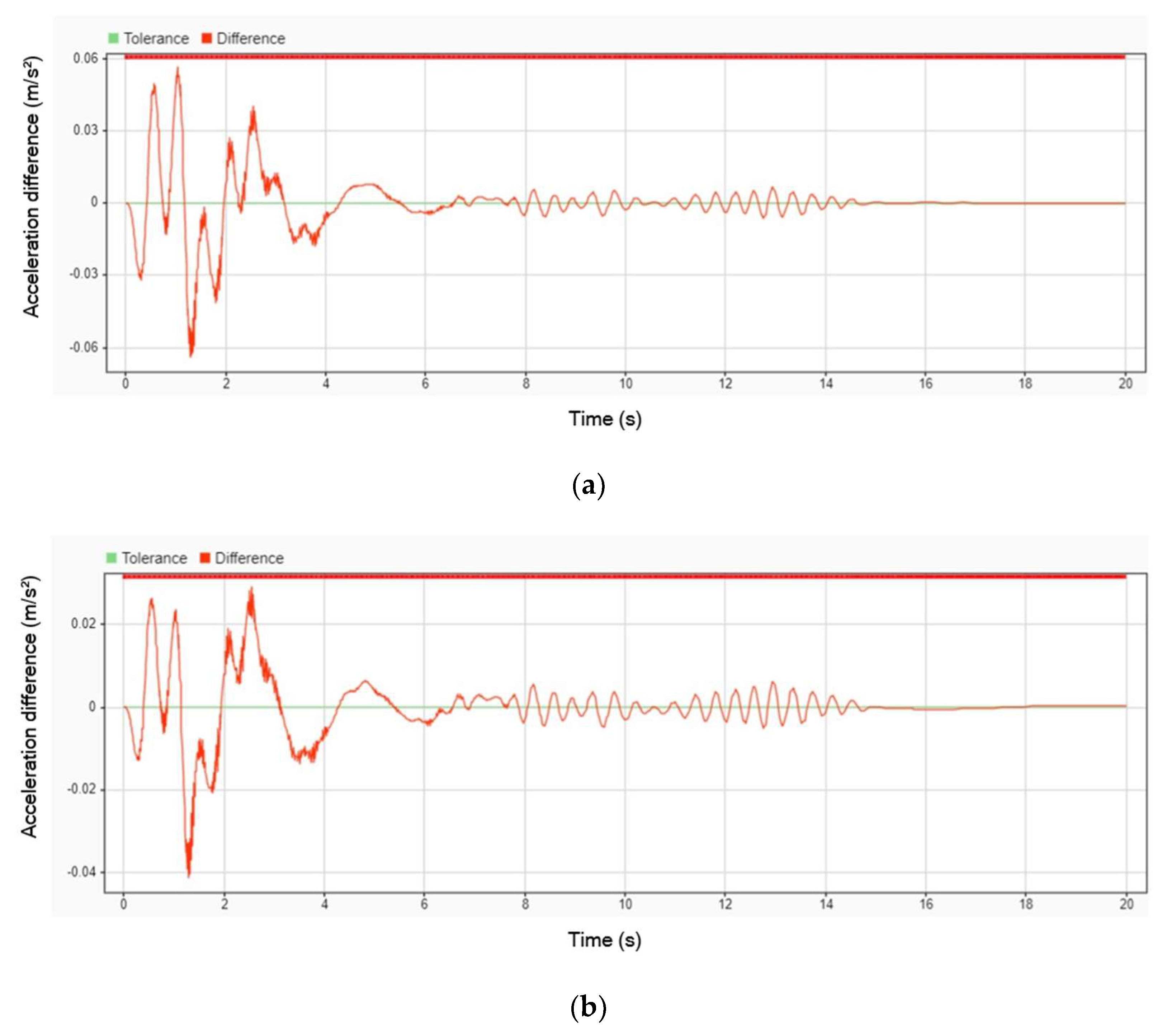
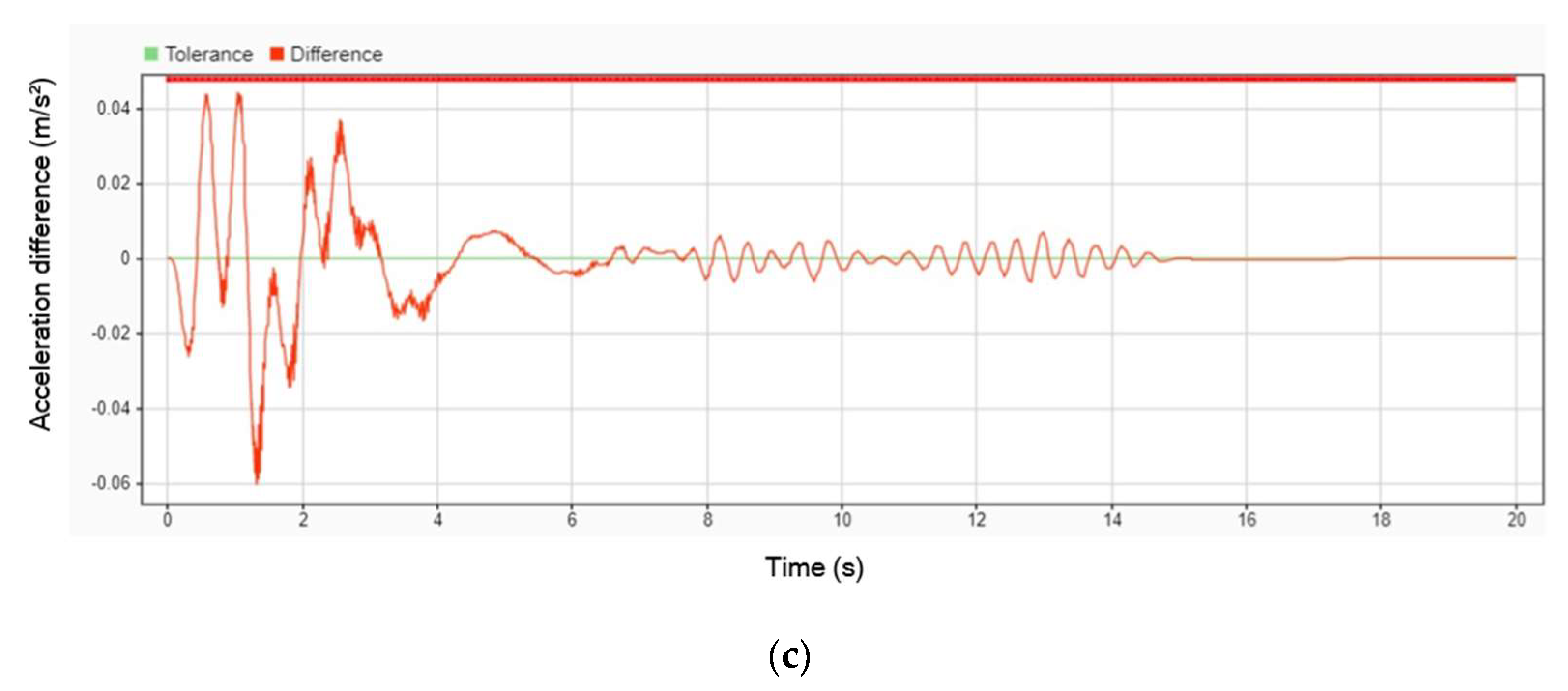
Figure 6 illustrates the acceleration response of the patient’s body with and without the DVA installed on the stretcher. The blue line represents the scenario without the DVA, while the orange line indicates the use of the DVA. Initially, during the first 4 s, the acceleration of all parts of the patient’s body fluctuates significantly, reflecting the direct impact of road-induced vibrations. However, after this initial period, the acceleration begins to stabilize, indicating that the DVA effectively mitigates oscillations and helps the system reach a steady state. This comparison underscores the role of the DVA in enhancing damping performance and improving patient stability during transport.

Figure 7 highlights the comparative performance of a stretcher equipped with a DVA against one without it in terms of the peak acceleration experienced by different parts of the patient’s body. The peak acceleration decreased by 8.66% for the head, 7.29% for the body, and 6.51% for the legs when the DVA was employed. During the first 4 s, all parts of the body experienced significant fluctuations due to road-induced vibrations. Although these fluctuations diminished after 4 s, small oscillations persisted, indicating that while the DVA significantly improves vibration damping, some residual movement remains, particularly during the transition to a steady state. These findings emphasize the importance of optimizing DVA designs for better performance across varying dynamic conditions.

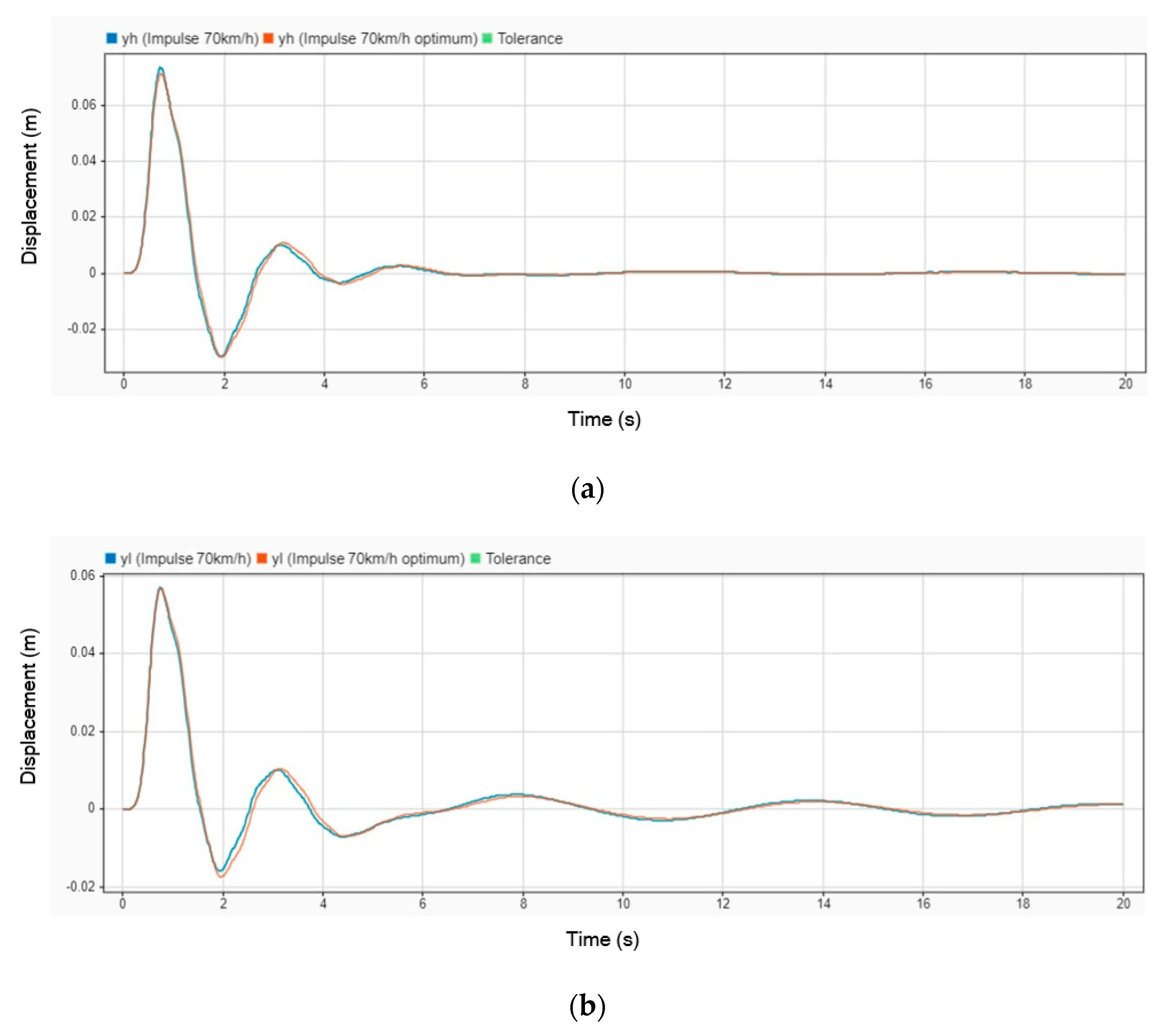
The next simulation involved an impulse input from the road while the vehicle traveled at a velocity of 50 km/h. Figure 8 presents the displacement response comparison between the stretcher with and without the DVA. In the graph, the blue line represents the displacement observed when no DVA is installed, while the orange line corresponds to the stretcher equipped with the DVA. The results indicate that the DVA effectively reduces displacement, particularly during the initial phase of oscillations, highlighting its role in minimizing the impact of road-induced disturbances and enhancing patient comfort during high-speed transport.

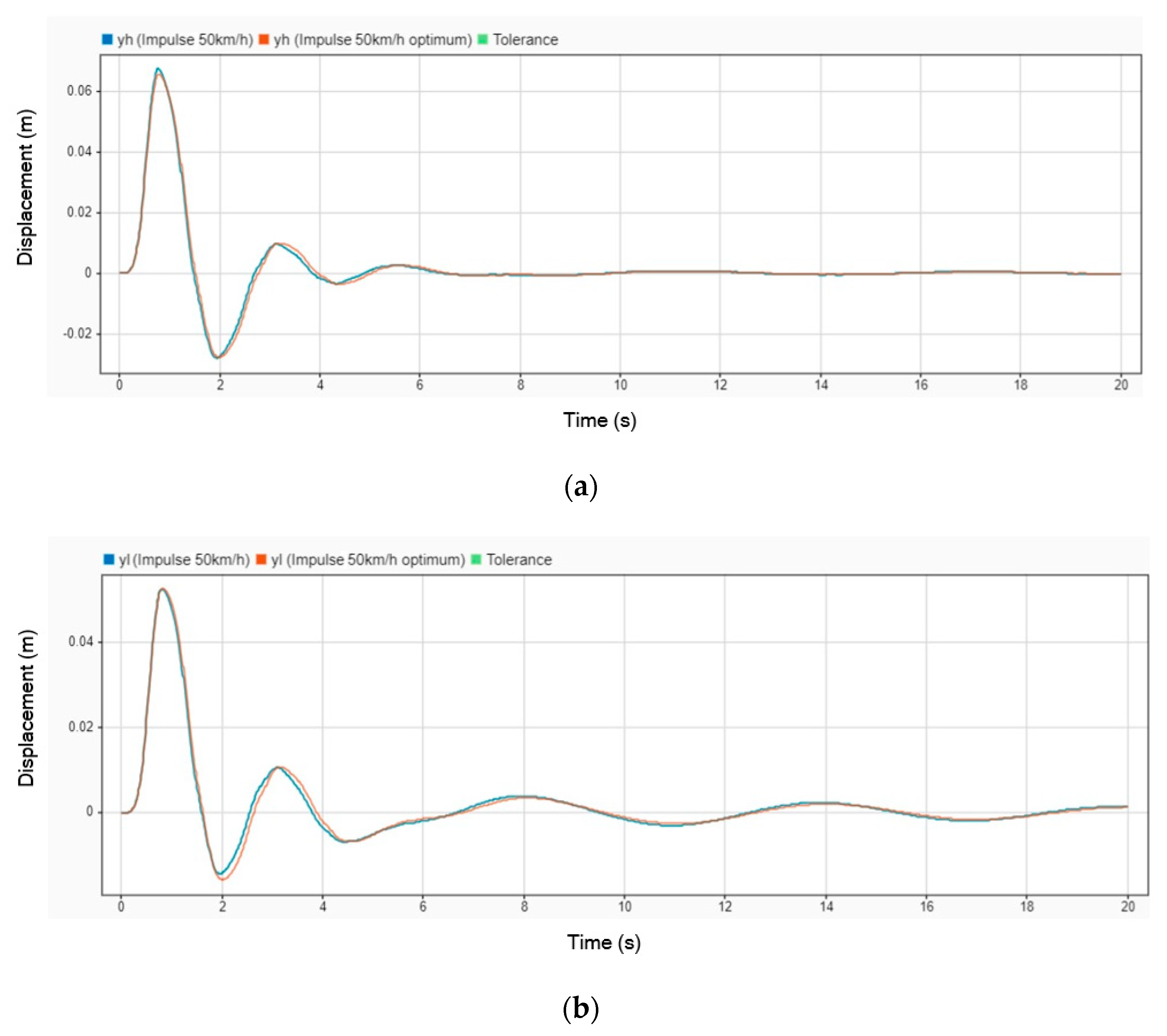
Figure 9 demonstrates the effectiveness of using a DVA in reducing vibrations at various parts of the patient’s body during transit. The peak amplitude of displacement at the head, body, and legs decreased by 5.44%, 4.78%, and 4.80%, respectively, when the DVA was employed. The results indicate that the patient’s head and body reached a steady state within 8 s, signifying effective vibration damping in these areas. However, the patient’s legs exhibited prolonged oscillations, persisting even after 20 s, suggesting a need for further refinement in the DVA’s design or positioning to ensure consistent damping across all body regions.

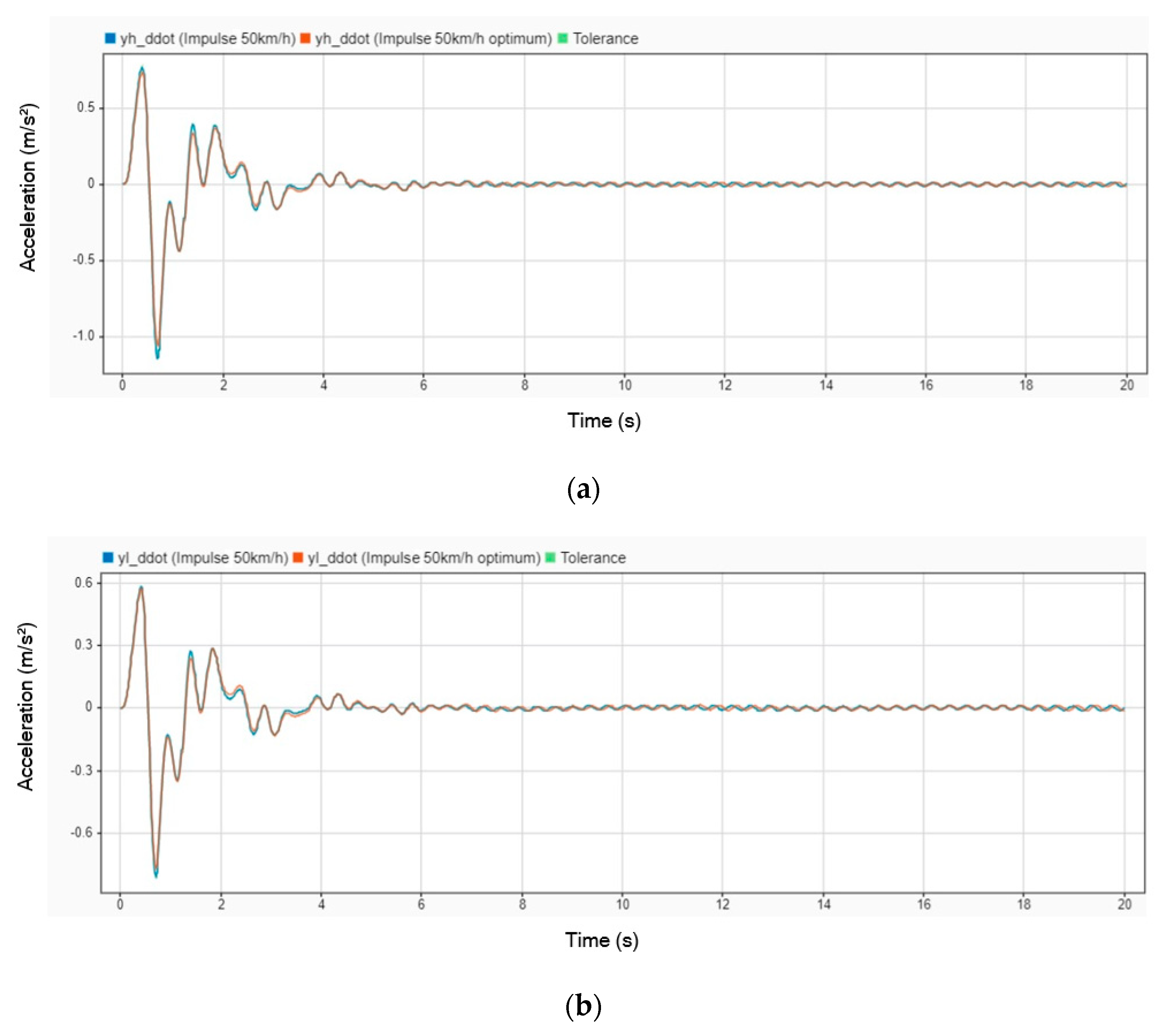
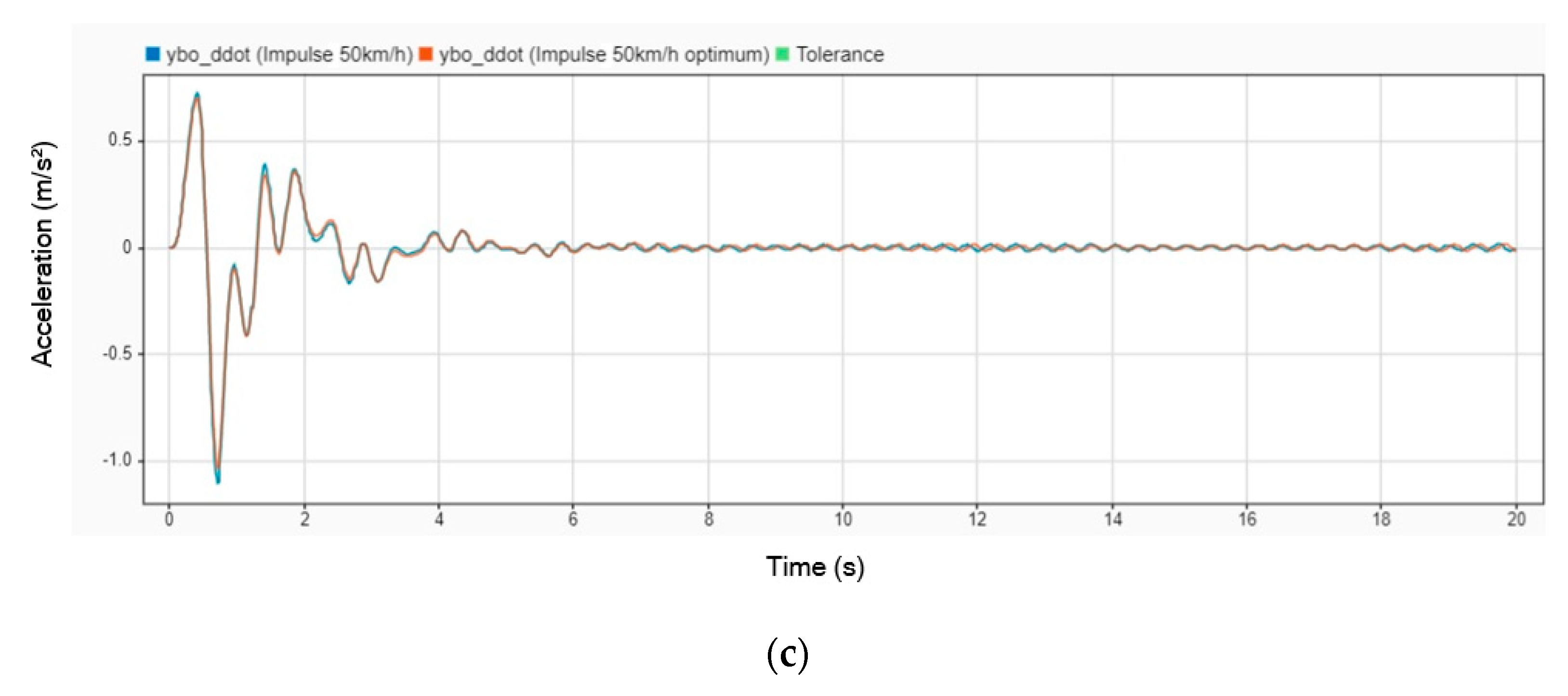
Figure 10 illustrates the comparison of acceleration responses for a stretcher with and without a DVA installed. The blue line represents the acceleration when no DVA is installed on the stretcher, while the orange line indicates the acceleration with the DVA in place. The results clearly show that the DVA reduces the amplitude of acceleration, demonstrating its effectiveness in dampening road-induced vibrations. This comparison highlights the DVA’s potential to enhance patient comfort and stability by mitigating abrupt acceleration fluctuations during transit.

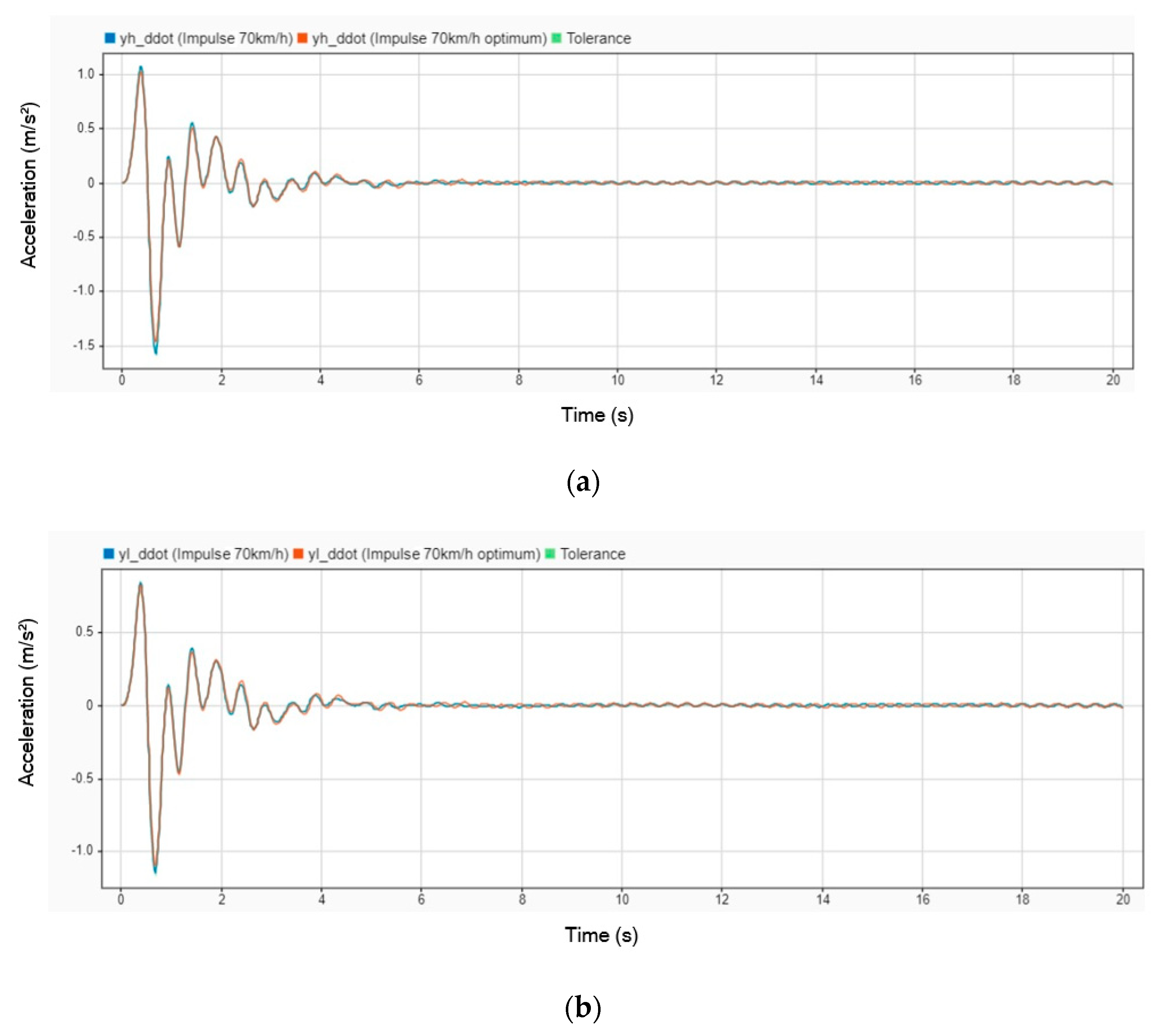
Figure 11 illustrates the difference in acceleration between using a DVA and not using one. The results clearly show that the peak amplitude of acceleration experienced by various parts of the body significantly decreases when a DVA is employed: the head’s peak acceleration is reduced by 12.24%, the legs’ by 8.25%, and the body’s by 10.97%. Despite these reductions, it is noteworthy that acceleration in all parts of the patient’s body continues to fluctuate even after 20 s, indicating that while the DVA effectively dampens peak vibrations, it does not completely eliminate oscillatory movements within this timeframe.

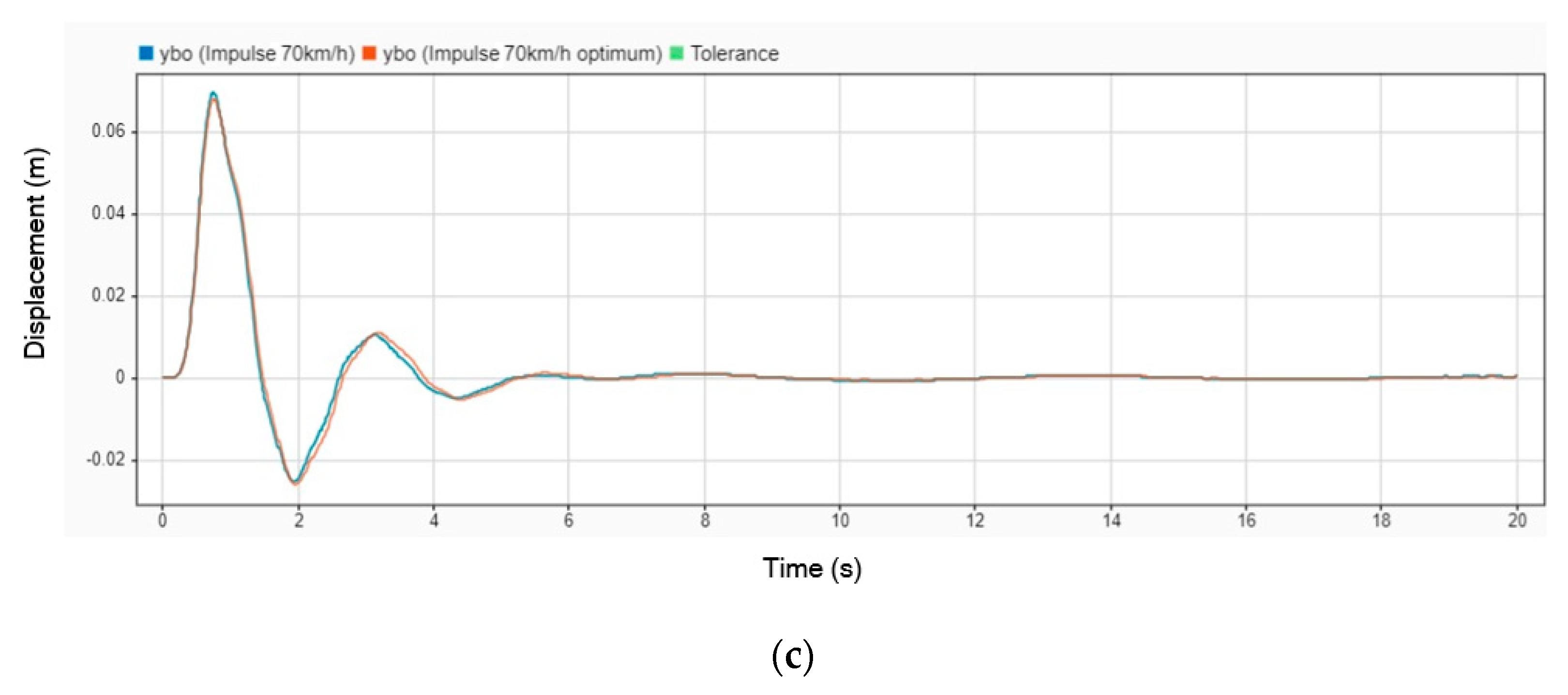
The next simulation was conducted with an impulse input from the road while the vehicle was traveling at a velocity of 70 km/h. Figure 12 illustrates the displacement comparison between using a DVA and not using one. In the graph, the blue line represents the displacement when the stretcher operates without a DVA installed, while the orange line represents the displacement when the DVA is installed. This comparison highlights the impact of the DVA in reducing displacement and enhancing the stability of the stretcher under dynamic road conditions.

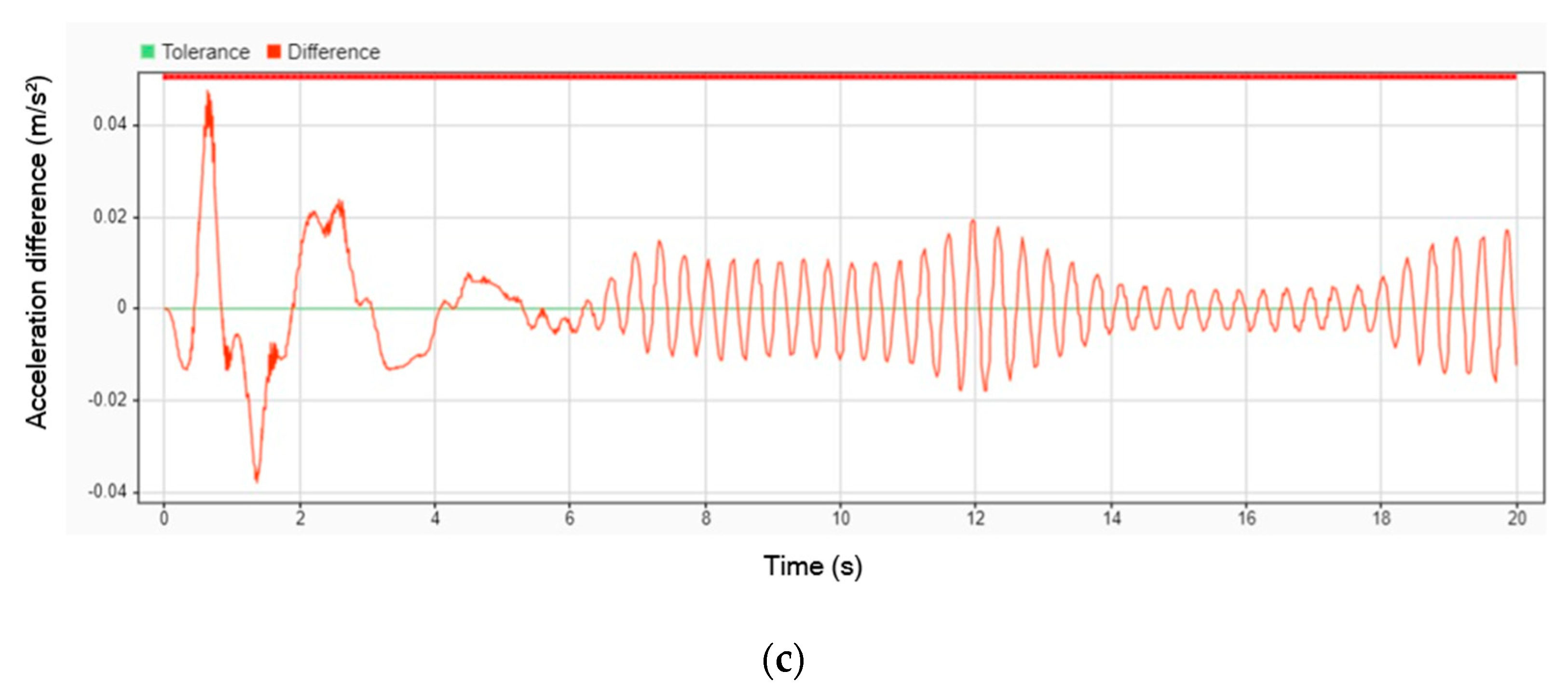
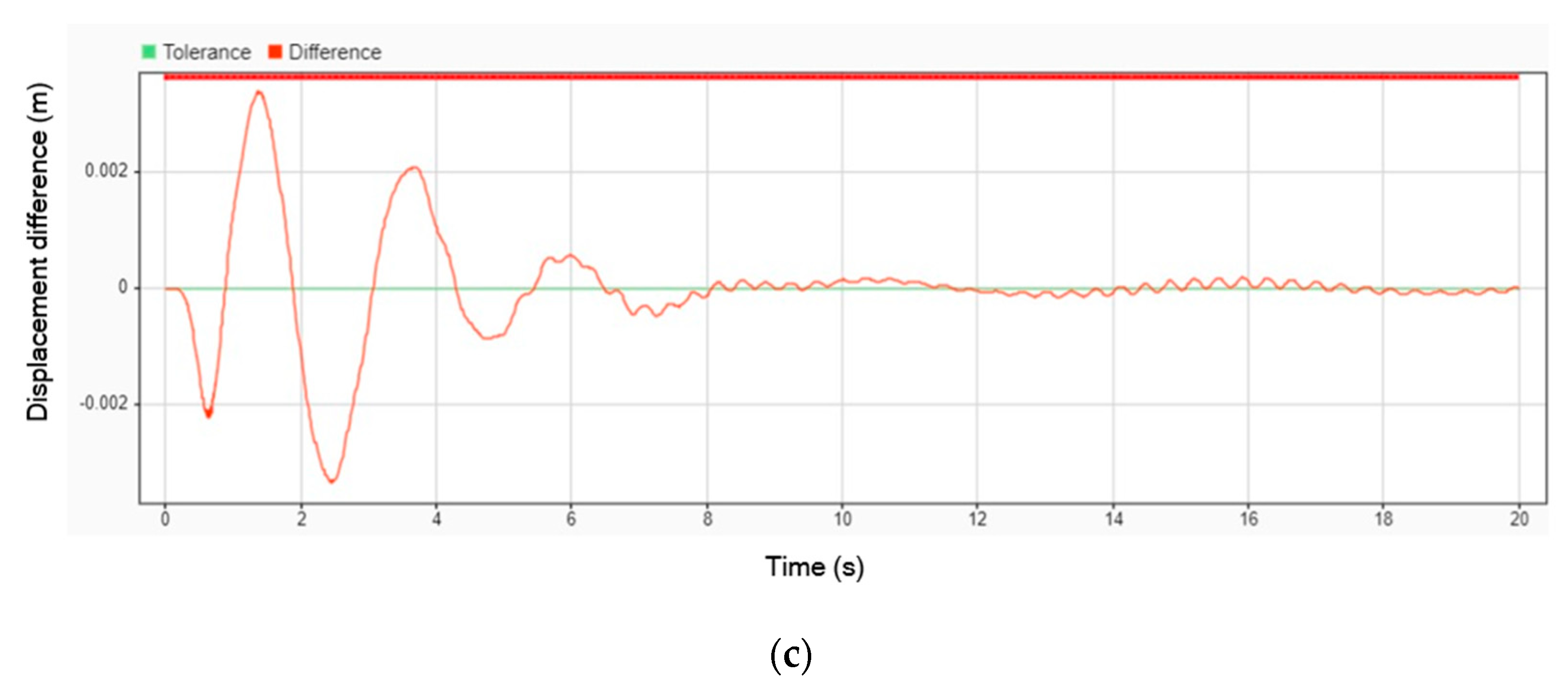
Figure 13 illustrates the difference in acceleration when using a DVA compared to not using one. The results show that the peak amplitude of displacement for the head, leg, and body decreased by 6.67%, 5.10%, and 4.92%, respectively, when the DVA was employed. Notably, the patient’s head and body showed significant stabilization, with their movements steadying after 7 s. However, the patient’s legs continued to oscillate even after 20 s, indicating that while the DVA effectively dampens vibrations in certain body parts, its impact on leg oscillations is less pronounced within the observed timeframe.

Figure 14 presents a comparison of acceleration with and without the use of a DVA on the stretcher. In this figure, the blue line represents the acceleration experienced when no DVA is installed, while the orange line represents the acceleration with the DVA installed. This comparison highlights the effectiveness of the DVA in reducing vibration-induced acceleration, showcasing its role in improving the overall stability and comfort of the stretcher system.

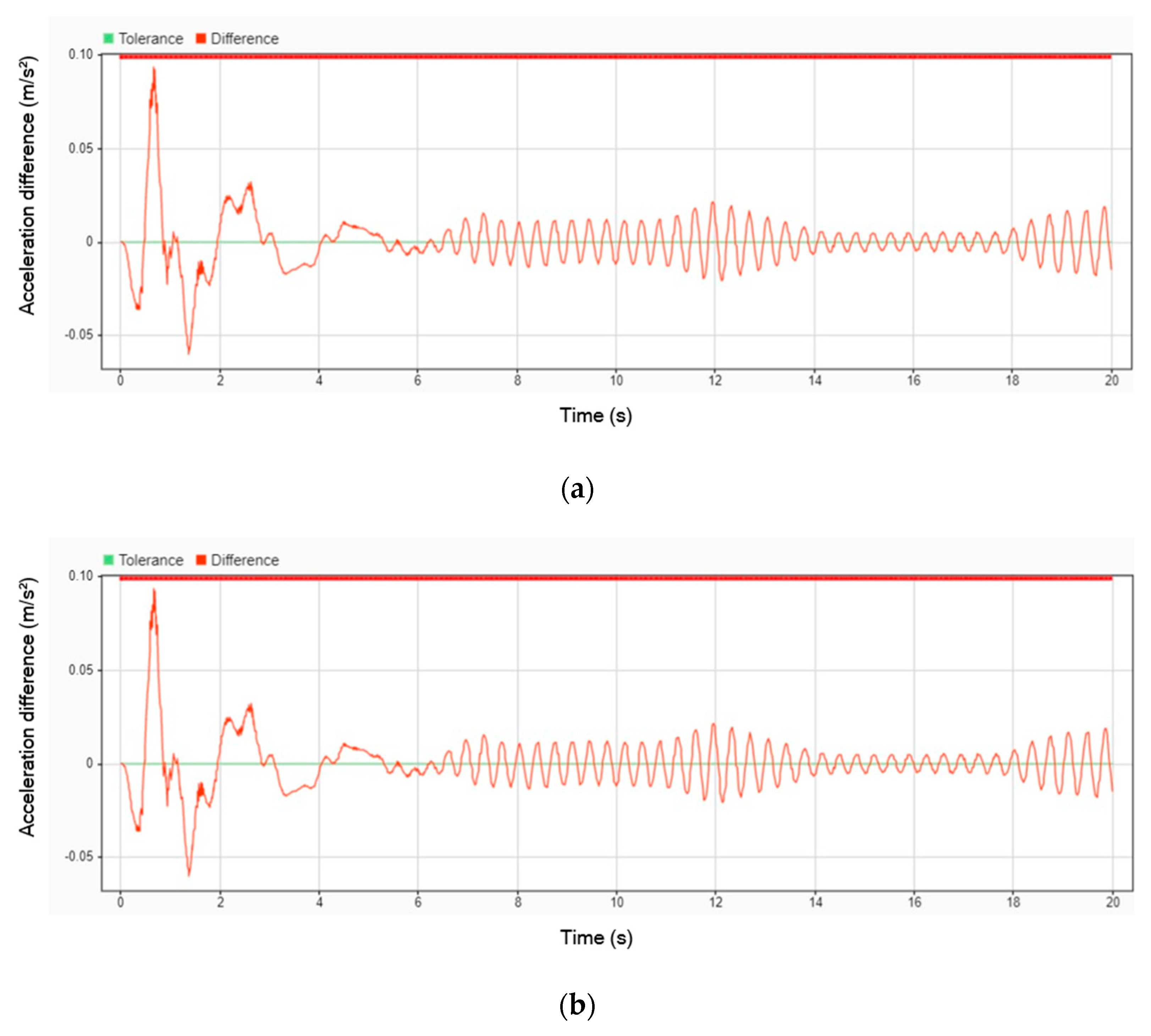
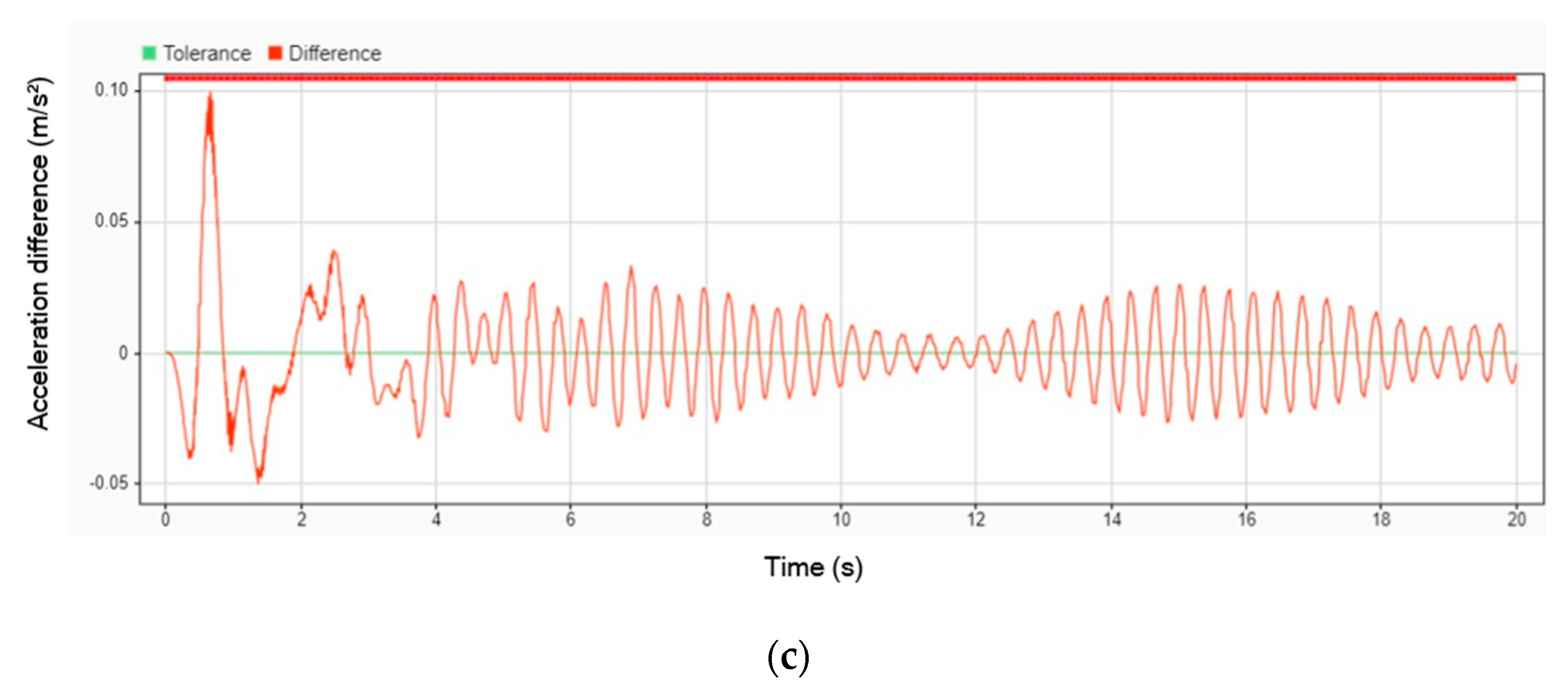
Figure 15 illustrates the difference in acceleration between using a DVA and not using one. The results indicate that the peak amplitude of acceleration decreased by 9.09% for the head, 6.62% for the legs, and 9.01% for the body when the DVA was employed. Despite these reductions, all parts of the patient’s body continued to oscillate throughout the entire simulation, with vibrations persisting even after 20 s. This suggests that while the DVA effectively reduces peak acceleration, it does not completely eliminate sustained oscillations over time.

It can be observed that for both displacement and acceleration, the percentage reduction follows a consistent order when ranked from the highest to the lowest: the head experiences the greatest reduction, followed by the body, and finally the legs. This indicates that the DVA has a more significant impact on the head and body compared to the legs. For displacement specifically, the percentage reduction varies with vehicle speed. The greatest reduction was observed at a speed of 70 km/h, followed by 50 km/h, and the smallest reduction occurred at 30 km/h. This suggests that the DVA’s effectiveness in minimizing displacement is more pronounced at higher speeds. In contrast, for acceleration, the order of percentage reduction based on speed is slightly different. The highest reduction was seen at 50 km/h, followed by 70 km/h, with the lowest reduction occurring at 30 km/h. This indicates that the DVA’s ability to reduce acceleration depends on the interaction between speed and the vibration dynamics of the system.

4. Conclusions

The study demonstrates the effectiveness of a dynamic vibration absorber (DVA) in reducing vibrations experienced by a stretcher during vehicle transit. Optimized parameters, determined using MATLAB Simulink and genetic algorithms, showed that the tournament and random methods identified the best parameters in only five iterations, compared to ten iterations for the roulette wheel method. Simulations revealed that the DVA effectively reduces displacement and acceleration, with the most significant reductions observed in the head, followed by the body and legs. For displacement, the highest reductions occurred at 70 km/h, followed by 50 km/h and 30 km/h, while acceleration reduction was most pronounced at 50 km/h. Despite these improvements, minor oscillations, particularly in the legs, persisted beyond 20 s, indicating potential for further design refinement. Overall, the DVA enhances stretcher stability and patient comfort, making it a valuable tool for improving safety during ambulance transport.