Lens Distortion Measurement and Correction for Stereovision Multi-Camera System †
Abstract
1. Introduction
2. Background Knowledge and Review of Related Works
3. Problem Statement
4. Implementation of Lens Distortion Correction
4.1. The Experimental Setup
4.2. The Calibration Process
4.3. Camera Evaluation Based on Distortion Coefficients
5. Evaluation of Lens Distortion Correction and Its Impact on Stereovision-Based Distance Measurement
5.1. Evaluation of the Improvement in the Line Curvature After Lens Distortion Correction
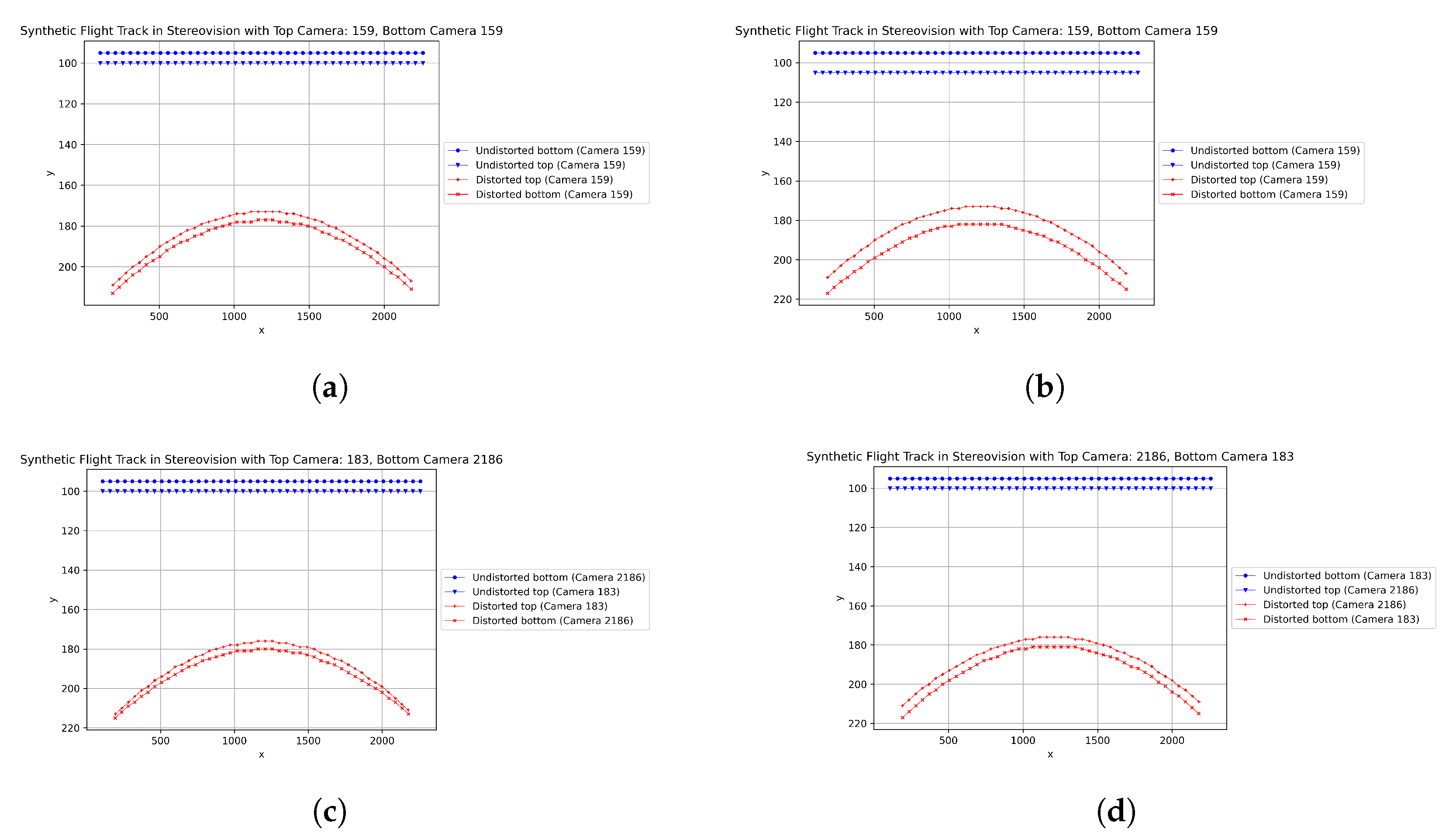
5.2. Evaluation of the Lens Distortion Effect on Stereovision
- Track 1: = 95 px, = 100 px, and = 5 px corresponding to d = 600 m;
- Track 2: = 95 px, = 105 px, and = 10 px corresponding to d = 300 m.
6. Results and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- van Erp, T.; Carvalho, N.G.P.; Gerolamo, M.C.; Gonçalves, R.; Rytter, N.G.M.; Gladysz, B. Industry 5.0: A new strategy framework for sustainability management and beyond. J. Clean. Prod. 2024, 461, 142271. [Google Scholar] [CrossRef]
- Gradolewski, D. Sensors and Algorithms in Industry 4.0: Security and Health Preservation Applications. Ph.D. Thesis, Blekinge Tekniska Högskola, Karlskrona, Sweden, 2021. [Google Scholar]
- Gradolewski, D.; Dziak, D.; Kaniecki, D.; Jaworski, A.; Skakuj, M.; Kulesza, W.J. A Runway Safety System Based on Vertically Oriented Stereovision. Sensors 2021, 21, 1464. [Google Scholar] [CrossRef] [PubMed]
- Gradolewski, D.; Dziak, D.; Martynow, M.; Kaniecki, D.; Szurlej-Kielanska, A.; Jaworski, A.; Kulesza, W.J. Comprehensive Bird Preservation at Wind Farms. Sensors 2021, 21, 267. [Google Scholar] [CrossRef] [PubMed]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kannala, J.; Brandt, S.S. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1335–1340. [Google Scholar] [CrossRef] [PubMed]
- Brown, D. Decentering distortion of lenses. Photogramm. Eng. 1966, 32, 444–462. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Heikkila, J. Geometric camera calibration using circular control points. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1066–1077. [Google Scholar] [CrossRef]
- Rahman, T.; Krouglicof, N. An Efficient Camera Calibration Technique Offering Robustness and Accuracy Over a Wide Range of Lens Distortion. IEEE Trans. Image Process. 2012, 21, 626–637. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, L.; Gómez, L.; Sendra, J.R. An Algebraic Approach to Lens Distortion by Line Rectification. J. Math. Imaging Vis. 2009, 35, 36–50. [Google Scholar] [CrossRef]
- Janos, I.; Benesova, W. Improving radial lens distortion correction with multi-task learning. Pattern Recognit. Lett. 2024, 183, 147–154. [Google Scholar] [CrossRef]
- Chuang, J.H.; Chen, H.Y. Alleviating Radial Distortion Effect for Accurate, Iterative Camera Calibration Using Principal Lines. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Duda, A.; Frese, U. Accurate Detection and Localization of Checkerboard Corners for Calibration. In Proceedings of the British Machine Vision Conference, Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 120, 122–125. [Google Scholar]
- Raspberry Pi High Quality Camera. Available online: https://datasheets.raspberrypi.com/hq-camera/hq-camera-product-brief.pdf (accessed on 14 October 2024).
- Sony IMX477 Matrix. Available online: https://docs.baslerweb.com/c125-0618-5m-p (accessed on 14 October 2024).



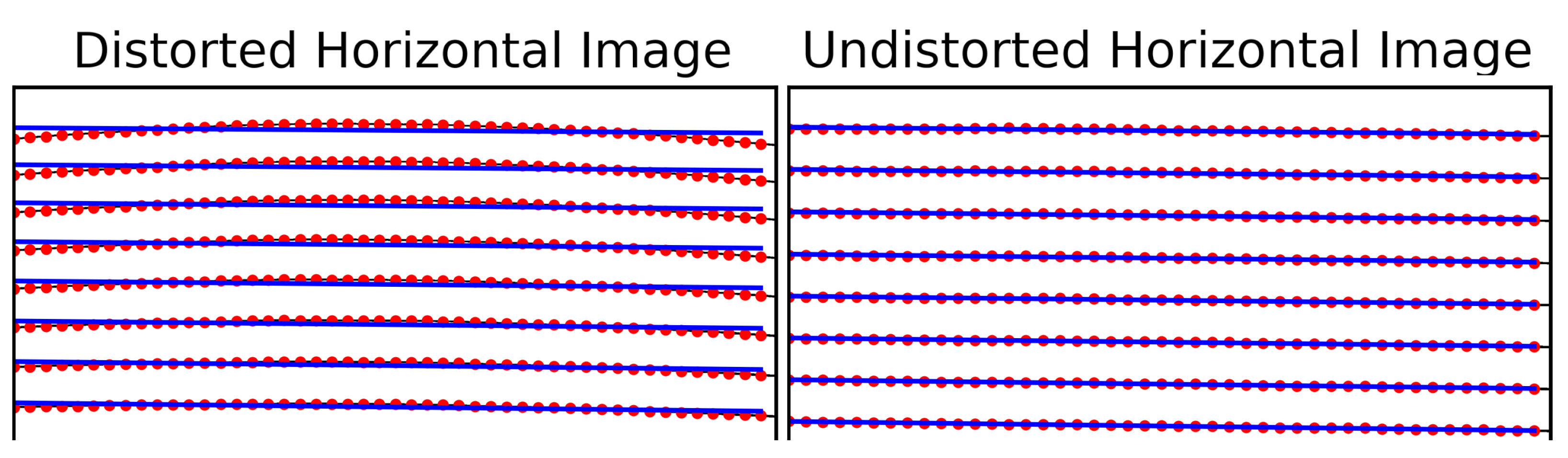
| Distortion Coefficients | ||||
|---|---|---|---|---|
| Camera ID | 159 | −0.217 | −0.024 | 0.158 |
| 183 | −0.243 | 0.067 | 0.077 | |
| 218 | −0.235 | 0.010 | 0.141 | |
| 223 | −0.224 | 0.042 | 0.053 | |
| 226 | −0.237 | 0.027 | 0.134 | |
| 247 | −0.241 | 0.009 | 0.162 | |
| 304 | −0.284 | 0.269 | −0.300 | |
| 401 | −0.266 | 0.203 | −0.192 | |
| 1726 | −0.200 | −0.292 | 0.828 | |
| 1855 | −0.262 | 0.149 | −0.112 | |
| 2186 | −0.247 | 0.109 | −0.041 | |
| mean | −0.241 | 0.052 | 0.083 | |
| sd | 0.024 | 0.145 | 0.291 | |
| Camera ID | Mean [px] | |||||||
|---|---|---|---|---|---|---|---|---|
| 159 | 183 | 218 | 223 | 226 | 401 | 2186 | ||
| Vertical [px] | 185.4 | 182.0 | 249.1 | 224.6 | 217.4 | 210.4 | 212.9 | 211.7 |
| Horizontal [px] | 114.4 | 116.6 | 71.6 | 99.5 | 107.1 | 117.3 | 106.5 | 118.9 |
| Mean [px] | 149.9 | 149.3 | 160.3 | 162.1 | 162.2 | 163.8 | 165.9 | 159.1 |
| Camera ID | Mean [px] | Improvement Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 159 | 183 | 218 | 223 | 226 | 401 | 2186 | |||
| Vertical [px] | 1.9 | 1.8 | 3.5 | 4.4 | 2.7 | 2.2 | 2.0 | 2.6 | 81.4 |
| Horizontal [px] | 4.4 | 2.5 | 6.9 | 5.0 | 3.7 | 4.8 | 2.3 | 4.2 | 28.3 |
| Mean [px] | 3.1 | 2.1 | 5.2 | 4.6 | 3.2 | 3.5 | 2.2 | 3.4 | 46.8 |
| Improvement Rate | 48.4 | 71.1 | 30.8 | 35.2 | 50.7 | 46.8 | 75.4 | 46.8 | |
| Max and min errors in disparity and distance for distorted Track 1 | |||
| Top↓, Bottom→ | 159 | 183 | 2186 |
| 159 | −0.7 px → 105 m (+17%) −0.8 px → 112 m (+19%) |
2.3 px → −187 m (−32%) 0.9 px → −90 m (−15%) |
3.5 px → −246 m (−41%) 2.5 px → −202 m (−34%) |
| 183 | −2.4 px → 576 m (+96%) −3.8 px → 1814 m (+302%) | −0.7 px → 105 m (+17%) −0.8 px → 110 m (+18%) |
1.8 px → −169 m (−27%) −0.5 px → 162 m (+10%) |
| 2186 | −3.0 px → 2540 m (+423%) −5.0 px → m | −1.0 px → 156 m (+26%) −3.4 px → 1302 m (+217%) | −0.8 px → 107 m (+18%) −0.8 px → 107 m (+18%) |
| Max and min errors in disparity and distance for distorted Track 2 | |||
| Top↓, Bottom→ | 159 | 183 | 2186 |
| 159 | −1.5 px → 52 m (+17%) −1.6 px → 56 m (+19%) |
1.5 px → −40 m (−13%) 0.1 px → −3 m (−1%) |
2.6 px → −63 m (−21%) 1.8 px → −45 m (−15%) |
| 183 | −3.2 px → 143 m (+48%) −4.5 px → 245 m (+82%) | −1.5 px → 52 m (+17%) −1.5 px → 52 m (+17%) |
1.0 px → −27 m (−9%) −1.2 px → 42 m (+14%) |
| 2186 | −4.8 px → 275 m (+92%) −5.9 px → 429 m (+143%) | −1.8 px → 65 m (+22%) −4.2 px → 217 m (+72%) | −1.5 px → 53 m (+18%) −1.7 px → 60 m (+20%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madejski, G.; Zbytniewski, S.; Kurowski, M.; Gradolewski, D.; Kaoka, W.; Kulesza, W.J. Lens Distortion Measurement and Correction for Stereovision Multi-Camera System. Eng. Proc. 2024, 82, 85. https://doi.org/10.3390/ecsa-11-20457
Madejski G, Zbytniewski S, Kurowski M, Gradolewski D, Kaoka W, Kulesza WJ. Lens Distortion Measurement and Correction for Stereovision Multi-Camera System. Engineering Proceedings. 2024; 82(1):85. https://doi.org/10.3390/ecsa-11-20457
Chicago/Turabian StyleMadejski, Grzegorz, Sebastian Zbytniewski, Mateusz Kurowski, Dawid Gradolewski, Włodzimierz Kaoka, and Wlodek J. Kulesza. 2024. "Lens Distortion Measurement and Correction for Stereovision Multi-Camera System" Engineering Proceedings 82, no. 1: 85. https://doi.org/10.3390/ecsa-11-20457
APA StyleMadejski, G., Zbytniewski, S., Kurowski, M., Gradolewski, D., Kaoka, W., & Kulesza, W. J. (2024). Lens Distortion Measurement and Correction for Stereovision Multi-Camera System. Engineering Proceedings, 82(1), 85. https://doi.org/10.3390/ecsa-11-20457







