Analysis of Multiple Emotions from Electroencephalogram Signals Using Machine Learning Models †
Abstract
1. Introduction
- Develop a suitable VAD model to categorize 16 emotions which is high when compared to the existing state-of-the-art techniques.
- Evaluate the performance of the machine learning model for 2-class, 4-class, and 16-class and hence, identify a suitable machine learning model for multiple class classification of emotion.
2. Methodology
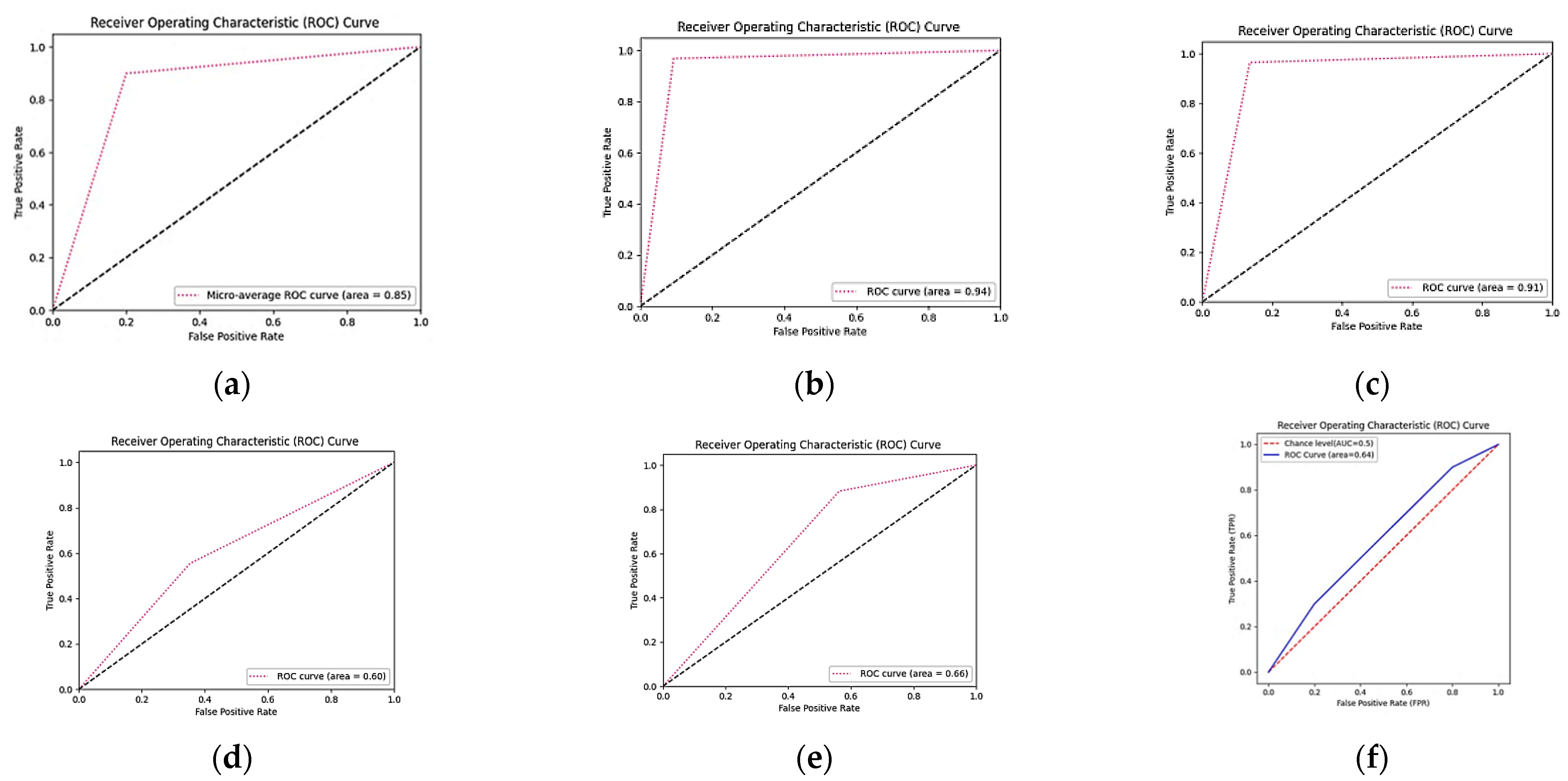
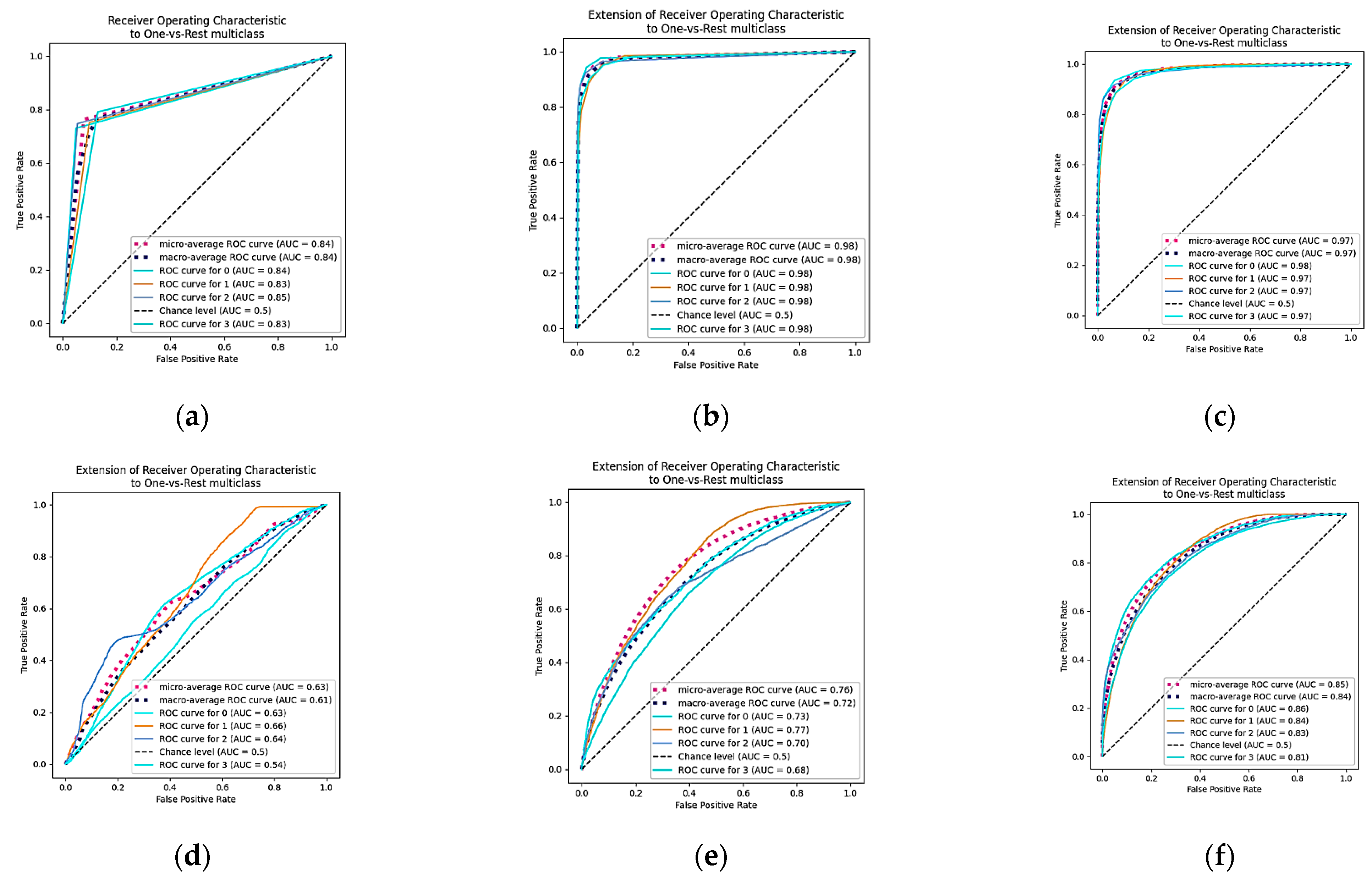
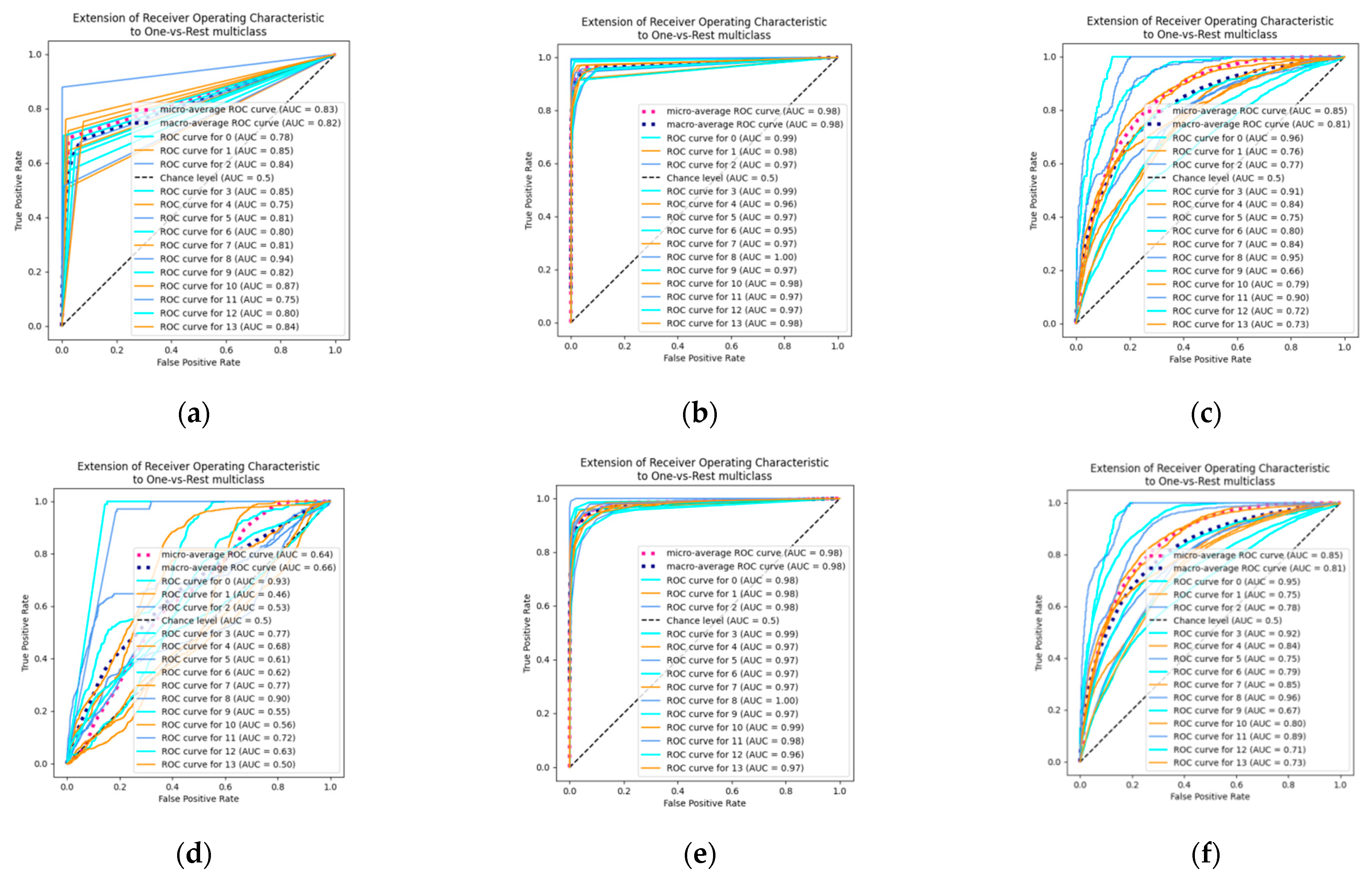
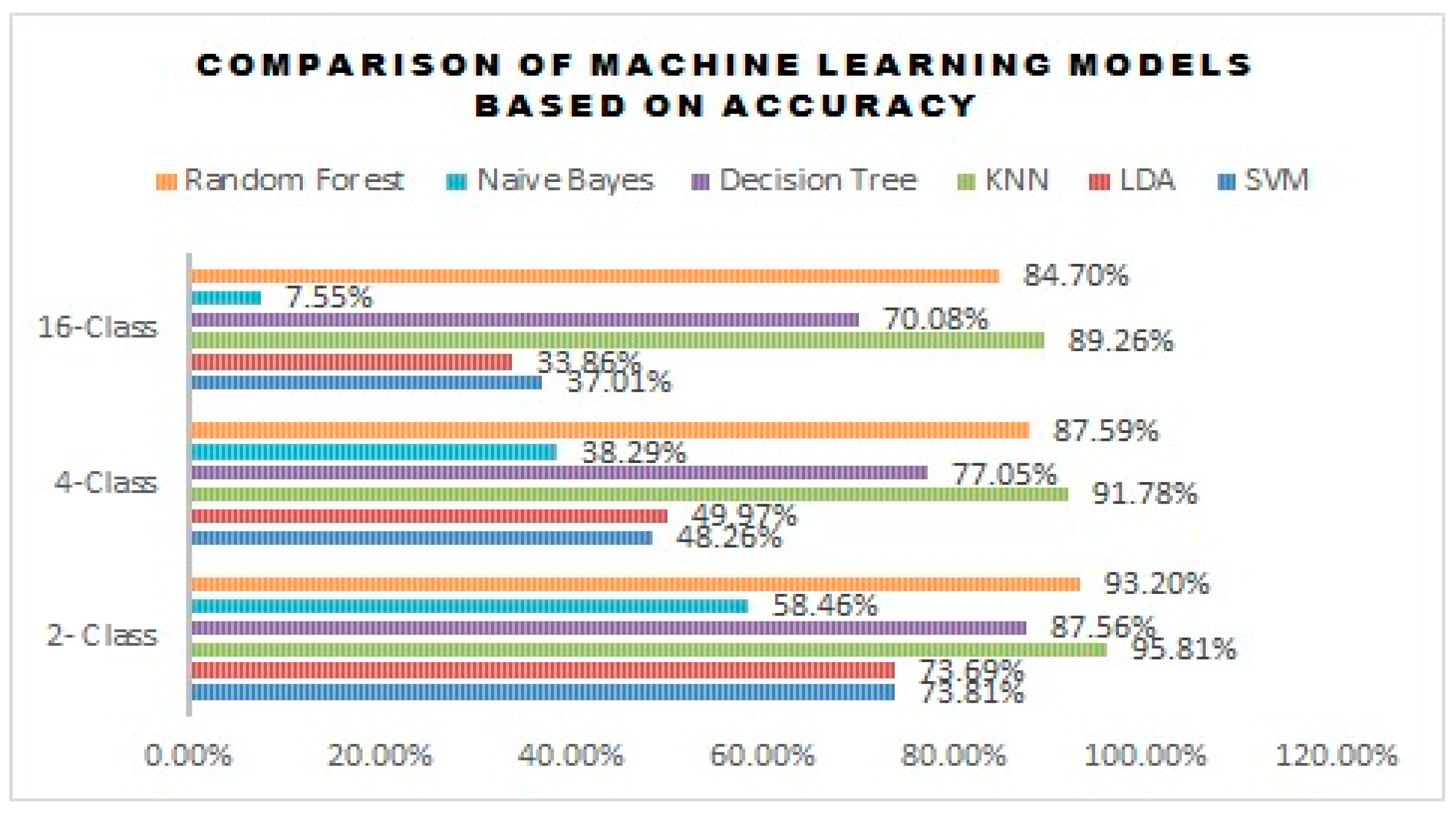
3. Result and Discussion
3.1. SVM
3.2. LDA
3.3. KNN
3.4. Decision Tree
3.5. Naive Bayes
3.6. Random Forest
3.7. Statistical Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Banu, N.M.; Sujithra, T.; Cherian, S.M. Performance Comparison of BCI Speller Stimuli Design. Mater. Today Proc. 2021, 45, 2821–2827. [Google Scholar] [CrossRef]
- Cao, G.; Ma, Y.; Meng, X.; Gao, Y.; Meng, M. Emotion Recognition Based On CNN. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8627–8630. [Google Scholar]
- Dabas, H.; Sethi, C.; Dua, C.; Dalawat, M.; Sethia, D. Emotion Classification Using EEG Signals; ACM: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow; R. O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Houssein, E.H.; Hammad, A.; Ali, A.A. Human Emotion Recognition from EEG-Based Brain–Computer Interface Using Machine Learning: A Comprehensive Review. In Neural Computing and Applications; Springer: London, UK, 2022; Volume 34. [Google Scholar] [CrossRef]
- Ivanova, E.; Borzunov, G. Optimization of Machine Learning Algorithm of Emotion Recognition in Terms of Human Facial Expressions. Procedia Comput. Sci. 2020, 169, 244–248. [Google Scholar] [CrossRef]
- Koelstra, S.; Mühl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. DEAP: A Database for Emotion Analysis; Using Physiological Signals. IEEE Trans. Affect. Comput. 2012, 3, 18–31. [Google Scholar] [CrossRef]
- Kusumaningrum, T.D.; Faqih, A.; Kusumoputro, B. Emotion Recognition Based on DEAP Database Using EEG Time-Frequency Features and Machine Learning Methods. J. Phys. Conf. Ser. 2020, 1501, 012020. [Google Scholar] [CrossRef]
- Lee, Y. Support Vector Machines for Classification: A Statistical Portrait. Methods Mol. Biol. 2010, 620, 347–368. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Ren, C.; Ge, Y.; Zhao, Q.; Yang, Y.; Shi, Y.; Zhang, X.; Hu, B. MTLFuseNet: A Novel Emotion Recognition Model Based on Deep Latent Feature Fusion of EEG Signals and Multi-Task Learning. Knowl.-Based Syst. 2023, 276, 110756. [Google Scholar] [CrossRef]
- Li, X.; Song, D.; Zhang, P.; Zhang, Y.; Hou, Y.; Hu, B. Exploring EEG Features in Cross-Subject Emotion Recognition. Front. Neurosci. 2018, 12, 15. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sourina, O. EEG-Based Dominance Level Recognition for Emotion-Enabled Interaction. In Proceedings of the IEEE International Conference on Multimedia and Expo, Melbourne, VIC, Australia, 9–13 July 2012; pp. 1039–1044. [Google Scholar] [CrossRef]
- Jehosheba Margaret, M.; Masoodhu Banu, N.M. Performance Analysis of EEG Based Emotion Recognition Using Deep Learning Models. Brain-Comput. Interfaces 2023, 10, 79–98. [Google Scholar] [CrossRef]
- Margaret, M.J.; Masoodhu Banu, N.M. A Survey on Brain Computer Interface Using EEG Signals for Emotion Recognition. AIP Conf. Proc. 2022, 2518, 040002. [Google Scholar]
- Mowla, M.R.; Cano, R.I.; Dhuyvetter, K.J.; Thompson, D.E. Affective Brain-Computer Interfaces: Choosing a Meaningful Performance Measuring Metric. Comput. Biol. Med. 2020, 126, 104001. [Google Scholar] [CrossRef] [PubMed]
- Nandini, D.; Yadav, J.; Rani, A.; Singh, V. Design of Subject Independent 3D VAD Emotion Detection System Using EEG Signals and Machine Learning Algorithms. Biomed. Signal Process. Control. 2023, 85, 104894. [Google Scholar] [CrossRef]
- Liu, N.; Fang, Y.; Li, L.; Hou, L.; Yang, F.; Guo, Y. Multiple Feature Fusion for Automatic Emotion Recognition Using EEG Signals. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 896–900. [Google Scholar]
- Ozdemir, M.A.; Degirmenci, M.; Izci, E.; Akan, A. EEG-Based Emotion Recognition with Deep Convolutional Neural Networks. Biomed. Tech. 2021, 66, 43–57. [Google Scholar] [CrossRef]
- Pandey, P.; Seeja, K.R. Subject Independent Emotion Recognition from EEG Using VMD and Deep Learning. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1730–1738. [Google Scholar] [CrossRef]
- Sharma, A. Emotion Recognition Using Deep Convolutional Neural Network with Large Scale Physiological Data; University of South Florida: Tampa, FL, USA, 2018; Available online: https://scholarcommons.usf.edu/etd/7570 (accessed on 16 September 2023).
- Zangeneh Soroush, M.; Maghooli, K.; Setarehdan, S.K.; Nasrabadi, A.M. A Novel Approach to Emotion Recognition Using Local Subset Feature Selection and Modified Dempster-Shafer Theory. Behav. Brain Funct. 2018, 14, 17. [Google Scholar] [CrossRef] [PubMed]
- Theobald, O. Machine Learning for Absolute Beginners; Scatterplot Press: London, UK, 2017; Volume 4. [Google Scholar]
- Wang, J.; Wang, W. Review of the Emotional Feature Extraction and Classification Using EEG Signals. Cogn. Robot. 2021, 1, 29–40. [Google Scholar] [CrossRef]
- Yan, J.; Chen, S.; Deng, S. A EEG-Based Emotion Recognition Model with Rhythm and Time Characteristics. Brain Inform. 2019, 6, 7. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Q.M.J.; Zheng, W.-L.; Lu, B.-L. EEG-Based Emotion Recognition Using Hierarchical Network with Subnetwork Nodes. IEEE Trans. Cogn. Dev. Syst. 2017, 10, 408–419. [Google Scholar] [CrossRef]

| No. of Class | Categories |
|---|---|
| 2—(V) (A) | Valence(V), Arousal(A) |
| 4—(VA) | High Arousal High Valence (HAHV), High Arousal Low Valence (HALV), Low Arousal High Valence (LAHV), and Low Arousal Low Valence (LALV) |
| 16—(VAD) | Sadness, Shame, Guilt, Envy, Satisfaction, Relief, Hope, Interest, Fear, Disgust, Contempt, Anger, Pride, Elation, Joy, and Surprise |
| Name/Description | Version |
|---|---|
| CPU | Intel® Core™ i5 |
| RAM | 8 GB |
| OS | Windows 10 |
| Python | Python 3.11.5 |
| TensorFlow | TensorFlow 2.14.0 |
| Scikit-learn | Scikit-learn 1.3.1 |
| Anaconda | 2021.05 |
| Model | SVM-Linear | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |
| 2- Class | 73.81% | 72% | 64% | 65% |
| 4-Class | 48.26% | 46% | 42% | 42% |
| 16-Class | 37.01% | 35% | 37% | 35% |
| SVM-RBF | ||||
| 2- Class | 67.35% | 34% | 50% | 40% |
| 4-Class | 38.75% | 10% | 25% | 14% |
| 16-Class | 24.4% | 2% | 7% | 3% |
| Model | LDA | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |
| 2-Class | 73.69% | 70% | 66% | 67% |
| 4-Class | 49.97% | 49% | 43% | 44% |
| 16-Class | 33.86% | 28% | 29% | 25% |
| Model | KNN | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |
| 2-Class | 95.81% | 95% | 95% | 95% |
| 4-Class | 91.78% | 92% | 92% | 92% |
| 16-Class | 89.26% | 89% | 90% | 89% |
| Model | Decision Tree | |||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |||||
| Without Entropy | With Entropy | Without Entropy | With Entropy | Without Entropy | With Entropy | Without Entropy | With Entropy | |
| 2-Class | 86.71% | 87.56% | 85% | 86% | 85% | 86% | 85% | 86% |
| 4-Class | 76.39% | 77.05% | 75% | 76% | 76% | 77% | 76% | 77% |
| 16-Class | 69.68% | 70.08% | 67% | 68% | 68% | 68% | 67% | 68% |
| Model | Naive Bayes | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |
| 2- Class | 58.46% | 59% | 60% | 57% |
| 4-Class | 38.29% | 29% | 28% | 24% |
| 16-Class | 7.55% | 18% | 26% | 7% |
| Model | Random Forest | |||
|---|---|---|---|---|
| Accuracy | Precision | Recall | F1-Score | |
| 2- Class | 93.20% | 93% | 91% | 92% |
| 4-Class | 87.59% | 89% | 87% | 87% |
| 16-Class | 84.70% | 87% | 82% | 84% |
| Statistical Analysis for 2-class, 4-class, and 16-class | |
| 2-class | |
| Friedman Test Statistic | 19.60431 |
| p-value | 0.001482 |
| 4-class | |
| Friedman Test Statistic | 19.49275 |
| p-value | 0.001555 |
| 16-class | |
| Friedman Test Statistic | 20.0 |
| p-value | 0.001249 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margaret Matthew, J.; Banu Noordheen Mohammad Mustafa, M.; Selvarajan, M. Analysis of Multiple Emotions from Electroencephalogram Signals Using Machine Learning Models. Eng. Proc. 2024, 82, 41. https://doi.org/10.3390/ecsa-11-20398
Margaret Matthew J, Banu Noordheen Mohammad Mustafa M, Selvarajan M. Analysis of Multiple Emotions from Electroencephalogram Signals Using Machine Learning Models. Engineering Proceedings. 2024; 82(1):41. https://doi.org/10.3390/ecsa-11-20398
Chicago/Turabian StyleMargaret Matthew, Jehosheba, Masoodhu Banu Noordheen Mohammad Mustafa, and Madhumithaa Selvarajan. 2024. "Analysis of Multiple Emotions from Electroencephalogram Signals Using Machine Learning Models" Engineering Proceedings 82, no. 1: 41. https://doi.org/10.3390/ecsa-11-20398
APA StyleMargaret Matthew, J., Banu Noordheen Mohammad Mustafa, M., & Selvarajan, M. (2024). Analysis of Multiple Emotions from Electroencephalogram Signals Using Machine Learning Models. Engineering Proceedings, 82(1), 41. https://doi.org/10.3390/ecsa-11-20398






