Abstract
The regulation of the orientation of a flying aircraft under autopilot is a multifaceted and crucial task that requires accuracy and flexibility. To do this, it is essential to have a complex control system that is furnished with an advanced controller capable of actively monitoring and modifying the flying characteristics of the aircraft. This must possess the ability to react dynamically to a range of disturbances experienced throughout the flight, including turbulence, fluctuations in wind, and other pertinent environmental elements. Through real-time adjustment of the flying attitude, the control system guarantees that the aircraft maintains its planned trajectory, stability, and safety along the whole trajectory. Typically, PID controllers are used to regulate the longitudinal direction of flights. However, these offline tuned controllers lack automation and are unable to adjust parameters in response to inherent disturbances seen in practice. Thus, this paper proposes online tuning techniques that are created using artificial intelligence (AI) mechanisms, namely fuzzy logic and neural networks. The philosophy involved in this work is the online tuning of PID gain parameters by applying both aforementioned intelligent methods. The study also implements many classical PID tuning techniques and compares the most effective tuning method with online approaches. To evaluate the effectiveness of online controllers and the optimal classical PID controller, their performance was evaluated based on time-domain transient characteristics. The overall comprehensive analysis was conducted using MATLAB/Simulink. The analysis revealed that the intelligent fuzzy logic-based PID controller outperformed alternative tuning techniques with respect to time performance indices such as delay time, rise time, peak time, and settling time, which are improved by 5.88%, 3.26%, 8.05%, and 55.71%, respectively, when compared to classical PID tuning methods.
1. Introduction
The autopilot mode of operation is vital to an aircraft’s operation. However, this mode requires a smooth and robust controller to overcome sudden obstacles, change the flight’s orientation, or control the attitude of the flight. Normally, the longitudinal attitude control can be carried out along three axes, namely pitch axis, yaw axis, and roll axis. These movements can be obtained by varying the orientations of the ailerons, rudder, and elevators. The elevator controls the pitch axis, the rudder controls the yaw axis, and the aileron controls the roll axis of the flight. The flight model representing the roll axis, pitch axis, yaw axis, ailerons, elevators, and rudder is shown in Figure 1. If the flight must take off, elevators are oriented upward so the lift force is produced under the front part of the flight. This makes the flight move upward. Similarly, if the flight must descend, the elevator must be oriented downward. If the flight must change its path, then the rudder is oriented accordingly. If the flight wants to be rolled right, the right aileron must be oriented downward and the left aileron must be oriented upward. Similarly, for the flight’s left roll, the left aileron must be oriented downward, and the right aileron must be oriented upward. All these orientations are carried out by servo motors and are observed by the gyro sensor. The servo motors, when connected with the ailerons, should work efficiently so that the flight can roll smoothly without any disturbance for the passengers. This process is also applicable to military flights.
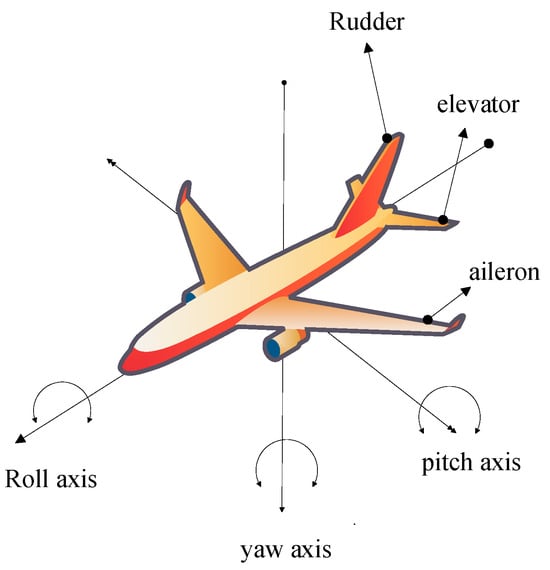
Figure 1.
Aircraft dynamics with its longitudinal rotations.
There are different control approaches developed in the literature for various key applications. Some of those key methods are: process control methods for the controller design [1,2]; online attitude control of autopilot flight [3]; aircraft’s fuselage control [4]; attitude control of mini-quadrotor [5]; stability control for four-rotor aircraft [6]; control of high-speed aircraft [7]; attitude control of UAV [8]; and flight in fixed time [9]. Furthermore, some advanced methods are investigated such as an improved attitude control for aircraft [10], inertia-based aerial vehicle control methods [11], simulators for the aircraft control [12], autopilot for the aerial vehicle [13], attitude control for the helicopter [14], control methods for the UAV flight [15], ADRC design for the flight [16], attitude control for the autopilot hypersonic vehicle [17], control structure for the micro-aerial vehicle with four rotors [18], roll attitude control for the fixed wing flight [19], fuzzy logic controller for longitudinal control of missiles [20], Eigen structure PID controller for longitudinal control of aircrafts [21], longitudinal control of small UAV using a RBF-type network-based PID control system [22], longitudinal attitude control by a dual fuzzy-PID control scheme for tail-sitter UAV [23], pitch control of the aircraft by using self-tuned Fuzzy-PID module, pitch attitude controller design for small UAVs, linear quadratic integral control strategy for pitch attitude control of aircrafts [24], etc. However, each control method is developed for a specific objective. So, their applicability to the longitudinal pitch attitude control for enhanced flight control dynamics needs to be investigated.
Thus, in this paper, various classical PID tuning methods and artificial intelligence (AI)-based PID tuning are realized. These are applied to the pitch control of the flight model caused by the servo motors of the elevators. From the analysis, the best classical PID tuning method is compared with the proposed fuzzy logic PID and ANN PID controllers using the time-domain index for the recommendation of the best tuning method.
2. Modeling of the Pitch Attitude Controller for the Aircraft
The feedback control model of the aircraft’s attitude control is shown in Figure 2. The transfer functions of aircraft dynamics block A(s) and the servo actuator block S(s) are shown in (1) and (2).
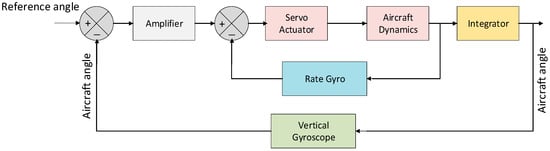
Figure 2.
Feedback control mechanism for pitch attitude controlling of the flight.
The rate gyro value is obtained as 1.2, and the controller is placed at the position of the amplifier, which obtains the feedback information from the integrator (about the orientation angle of the flight). The controller produces the necessary control signal by comparing the aircraft angle obtained from the integrator with the reference angle; thereby the flight is oriented in the specified direction provided by the controller with the help of the vertical gyroscope. Similarly, the gyro sensor obtains feedback information from the aircraft dynamics, and the information obtained from the gyro is fed to the servo actuator where the servo motor works to rotate the flight in the direction specified by the controller. The data from the servo actuator is obtained by the aircraft dynamics block, which consists of the rudder, elevator, and aileron operations, where the orientations of the flight take place.
2.1. Classical PID Controller Design
Classical PID controllers are normally used in many industrial applications due to their simplicity in structure and ease of design. They are designed by using various classical PID tuning methods, namely the error performance indices (EPI), open loop transient response (OLTR), and ultimate cycle (UC) methods, as depicted in Figure 3. The corresponding coefficients (KP, KI, and KD) of the PID module that are calculated using the above-said methods are displayed in Table 1. The OLTR and EPI methods are PI controller-tuning methods as they provide only proportional and integral gain parameters. UC is a PID controller-tuning method as it provides all proportional, integral, and derivative parameters.
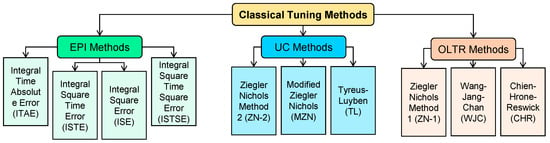
Figure 3.
Various classical PID tuning methods.

Table 1.
PID parameter computed with different classical tuning algorithms.
These offline design methods cannot handle real-time disturbances as the controller design process is independent from the presence of disturbance characteristics. So, the present research work aims to convert this offline tuning process into an online process by using AI methods like fuzzy logic technique and neural networks technique, as discussed in the following section.
2.2. Fuzzy Logic PID Controller Design
AI techniques provide many features such as control design, forecasting, regression analysis, etc. Even though these AI techniques provide better outputs compared to the offline PID tuning method, their efficacy depends on how efficiently the controller is trained. Fuzzy logic is an AI technology used for developing intelligence in control and information systems. Fuzzy logic is a simple system that depends on the degrees of the input and the output states, which hinge on the state of the input and the rate of change in the input state. The working mechanism and input/output of the fuzzy controller are shown in Figure 4 and Figure 5, respectively. This model is trained by using various membership functions. The input is considered as the deviation, and the outputs are PID coefficients. In the fuzzy logic system, the analog inputs are passed to the fuzzifier, which is converted to digital values through a process called fuzzification. This information is processed in the fuzzy inference system via the developed fuzzy rules. This processed information is again converted into analog values by using a process called defuzzification at the output. The Simulink diagram of the Fuzzy PID-based system is shown in Figure 6.
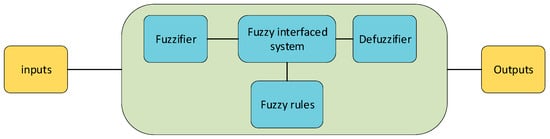
Figure 4.
Working mechanism of the fuzzy-based control process.
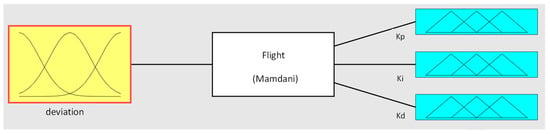
Figure 5.
Input and outputs of the fuzzy logic control system.
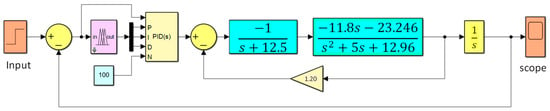
Figure 6.
Simulink model for the fuzzy logic-controlled PID controller for pitch control of flight.
2.3. Artificial Neural Networks PID (ANN-PID) Controller Design
In neural networks, there are three methods for controller design: (i) the Levenberg–Marquardt (LM) algorithm, (ii) the Bayesian Regularization (BR) algorithm, and (iii) the Scaled Conjugate Gradient (SCG) algorithm. The LM algorithm works on the principle of the least squares, which is also called the damped least square method. It is a commonly used method for solving nonlinear systems. This method is mainly used for small and medium-sized systems in ANNs. The BR algorithm is derived from the Bayes theorem. In this method, the nonlinear regression relations are converted into second-order linear regression-based mathematical equations. The SCG algorithm uses a linear search in each iteration. This method is mainly used for solving linear systems. This algorithm works with feedforward ANNs. These methods solve when all the errors are in the region of assumed values. The Simulink model of the ANN-PID-based system is shown in Figure 7.
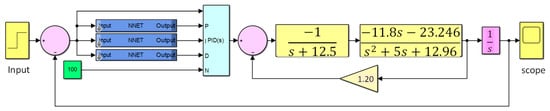
Figure 7.
Simulink block model for the ANN-controlled PID controller for pitch control of flight.
3. Simulation Results and Analysis
The transient responses of the classical PID controller-tuning methods are shown in Figure 8, Figure 9 and Figure 10. From these plots of the classical PID controller, it is experiential that the OLTR (Figure 8) and EPI (Figure 9) methods have longer settling times of around 20–40 s, while UC methods (Figure 10) have lesser settling times of around 2–4 s.
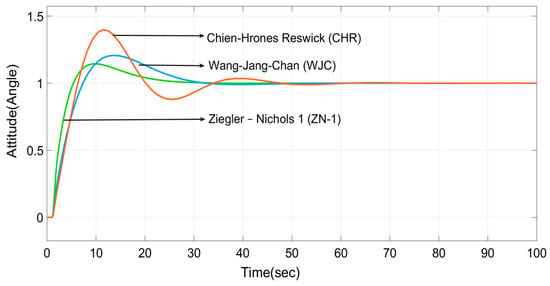
Figure 8.
Transient response for the OLTR methods.
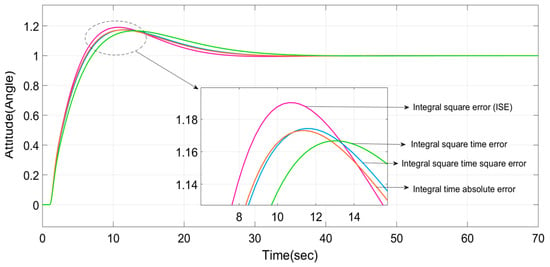
Figure 9.
Transient response for the EPI methods.
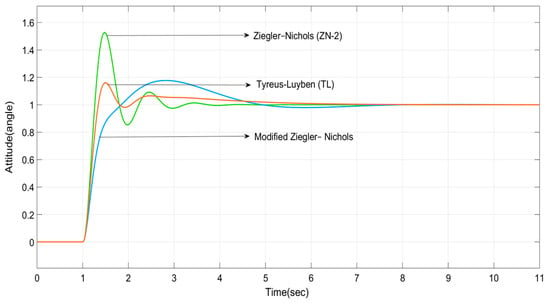
Figure 10.
Transient response for the UC methods.
The time-domain performance indexes are shown in Table 2. From these indexes, this tuning method, which leads to lower values of these indices, is considered the best tuning method. From this table, it is found that the TL method of classical PID design leads to superior values when matched to other methods. Thus, the TL method is declared as the best method for the controller design among the group of classical PID tuning methods. The transient responses of the ANN-PID controller trained with LM, BR, and SCG algorithms are shown in Figure 11. Their performance index is consolidated in Table 3. From this table, it is determined that the BR algorithm is the best ANN-based PID tuning method, as it shows the superior index values.

Table 2.
Time-domain performance index computed with various classical PID design methods.
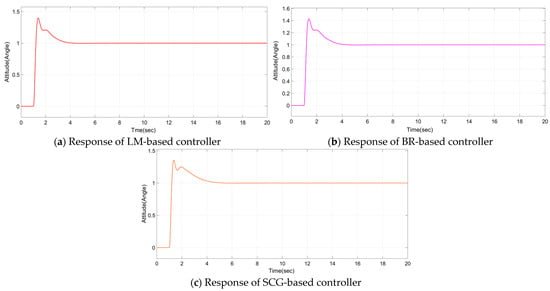
Figure 11.
Transient response for PID controller tuned with various ANN algorithms.

Table 3.
Time domain performance index computed with various ANN-PID design methods.
Furthermore, the transient responses of the Fuzzy-PID controller are shown in Figure 12. Finally, a comparative analysis is conducted among the best classical PID method (TL), the best ANN-PID method (BR), and the Fuzzy-PID method with the help of their performance index as presented in Table 4. From this table, it can be established that the Fuzzy-PID is the best PID tuning method, as it shows the superior index values.
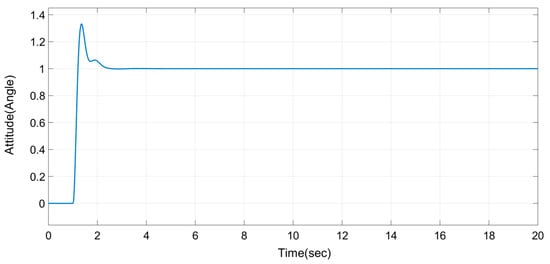
Figure 12.
Transient response for fuzzy logic-based PID controller.

Table 4.
Comparison of time domain parameters for classical and AI PID tuning methods.
4. Conclusions
This paper evaluates the usefulness of the classical PID tuning methods and AI-based PID tuning methods for the design of longitudinal pitch attitude control, with the objective of enhanced flight control dynamics. All the analysis is conducted by observing the consolidated time domain specifications presented, and it is concluded that the fuzzy logic-trained PID controller provides the best response over the ANN-PID controller and classical TL-PID controllers. Hence, the Fuzzy-PID controller is recommended for the controller design of the flight’s longitudinal pitch attitude control.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Chakravarthi, M.K.; Kumar, Y.V.P.; Reddy, G.P. Potential Technological Advancements in the Future of Process Control and Automation. In Proceedings of the 2024 IEEE Open Conference of Electrical, Electronic and Information Sciences (eStream), Vilnius, Lithuania, 25 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Karthik, R.; Hari, A.S.; Pavan Kumar, Y.V.; Pradeep, D.J. Modelling and Control Design for Variable Speed Wind Turbine Energy System. In Proceedings of the 2020 International Conference on Artificial Intelligence and Signal Processing (AISP), Amaravati, India, 10–12 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Pavan Kumar, Y.V.; Bhimasingu, R.; Jyothi, M.; Ramakrishna, B. Real Time and High Fidelity Controller Design for Hardware In the Loop (HIL) Testing of Flight Attitude Control. In Proceedings of the 2014 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kanyakumari, India, 10–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1217–1222. [Google Scholar] [CrossRef]
- Srikar, K.V.P.; Kumar, Y.V.P.; Pradeep, D.J.; Reddy, C.P. Investigation on PID Controller Tuning Methods for Aircraft Fuselage Temperature Control. In Proceedings of the 2020 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Marrakech, Morocco, 25–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zhongli, M.; Huixin, L.; Qianqian, L.; Yanming, G.; Zhongli, M.; Zuoyong, L. Design of Flight Attitude Control Model for the Mini-Quadrotor. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1433–1437. [Google Scholar] [CrossRef]
- Hongpeng, T.; Wei, B. Stability Control of Flight Attitude Angle for Four Rotor Aircraft. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 6–9 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 332–336. [Google Scholar] [CrossRef]
- Xin, W. Design of Fine Attitude Flight Control for a Highspeed Test Aircraft. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 22–24 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1961–1964. [Google Scholar] [CrossRef]
- Chen, H.; He, K.; Qian, W. Attitude Control of UAV Based on PI Dynamic Inversion. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 10668–10672. [Google Scholar] [CrossRef]
- Huang, B.; Li, A.J.; Guo, Y.; Wang, C.Q.; Zhang, Y. Fixed-Time Attitude Control for Spacecraft without Unwinding. In Proceedings of the 2017 International Conference on Mechanical, System and Control Engineering (ICMSC), St. Petersburg, Russia, 19–21 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 333–337. [Google Scholar] [CrossRef]
- Calugaru, G.; Danisor, E.-A. Improved Aircraft Attitude Control Using Generalized Predictive Control Method. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 101–106. [Google Scholar] [CrossRef]
- Xinghua, L. Flight Stability Control of Unmanned Aerial Vehicle Based on Micro Inertia Attitude Adjustment. In Proceedings of the 2018 IEEE International Conference of Safety Produce Informatization (IICSPI), Chongqing, China, 10–12 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 276–280. [Google Scholar] [CrossRef]
- Yoshitani, N.; Hashimoto, S.; Kimura, T.; Motohashi, K.; Ueno, S. Flight Control Simulators for Unmanned Fixed-Wing and VTOL Aircraft. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 3211–3216. [Google Scholar]
- Rao, J.; Gao, T.; Jiang, Z.; Gong, Z. Flight Control System of a Robotic Portable Unmanned Aerial Vehicle. In Proceedings of the 2010 2nd International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 540–544. [Google Scholar] [CrossRef]
- Rasheed, A. Helicopter Attitude Control. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ke, L.; Chun-Sheng, L.; Zheng-Zhong, W.; Qi-You, C. Design Flight Control System for UAV Full Envelope Flight. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 487–490. [Google Scholar] [CrossRef]
- Ma, S.; Sun, M.; Chen, Z. Interactive ADRC Design for Flight Attitude Control. In Proceedings of the 2017 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, China, 26–27 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 611–616. [Google Scholar] [CrossRef]
- Xin, W.; Feng, D.; Yi, L. Attitude control of unmanned hypersonic test vehicle. In Proceedings of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, H.; Cheng, X. A Design of Flight Control System for Four-Rotor Micro Aerial Vehicle. In Proceedings of the 2015 International Conference on Computational Intelligence and Communication Networks (CICN), Jabalpur, India, 12–14 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1447–1451. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, W.; Guo, C.; Zhang, Z.; Li, P. Simulation Research on Roll Attitude Initialization Algorithm for Fixed Wing Canards. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1292–1296. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, J.; Song, C.; Cao, H. Design of Longitudinal Control System for Target Missiles Based on Fuzzy Adaptive PID Control. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 398–402. [Google Scholar] [CrossRef]
- Ahmed, W.; Li, Z.; Istan, M.; Anwar, M.B. Multi-Objective Eigenstructure Assignment-PID Based Controller Design for Longitudinal Motion of Aircraft. In Proceedings of the 2019 5th International Conference on Control Science and Systems Engineering (ICCSSE), Shanghai, China, 14–16 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 40–44. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.; Geng, Q. Research of RBF Neural Network PID Control Algorithm for Longitudinal Channel Control of Small UAV. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1824–1827. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Xi, L. Adaptive Dual Fuzzy PID Control Method for Longitudinal Attitude Control of Tail-Sitter UAV. In Proceedings of the 2016 22nd International Conference on Automation and Computing (ICAC), Colchester, UK, 7–8 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 378–382. [Google Scholar] [CrossRef]
- Hamid, T.; Babar, M.Z.; Hassan, M.U.; Hussain, M.F. Pitch Attitude Control for an Aircraft Using Linear Quadratic Integral Control Strategy. In Proceedings of the 2019 22nd International Multitopic Conference (INMIC), Islamabad, Pakistan, 29–30 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).