Theoretical Study and Verification of the Mechanical Properties of Concave Honeycomb Structures Based on Additive Manufacturing ^†

Abstract

This paper focuses on the internal honeycomb structure of flexible skins for morphing aircraft, specifically targeting a unique concave honeycomb structure. By selecting specific honeycomb cells and simplifying their cell walls to beams, the equivalent elastic modulus and shear modulus were derived using the principle of virtual work. The cell was also simplified to an orthotropic plate, and the equivalent bending stiffness was derived using the principle of equivalent deformation energy. Using additive manufacturing methods and photosensitive resin materials, a series of honeycomb structure test pieces were manufactured and subjected to mechanical performance tests. The stress–strain curves and load-deflection curves of the honeycomb structures were obtained, and the equivalent elastic modulus, equivalent shear modulus, and equivalent bending stiffness were calculated from the experimental data. The theoretical values of the equivalent mechanical properties were compared with the experimental values, with errors of 4.38%, 16.67%, and 15.47% for the equivalent elastic modulus, equivalent shear modulus, and equivalent bending stiffness, respectively. Finally, the causes of the errors were analyzed, and this method has significant value for the application of such honeycomb structures.

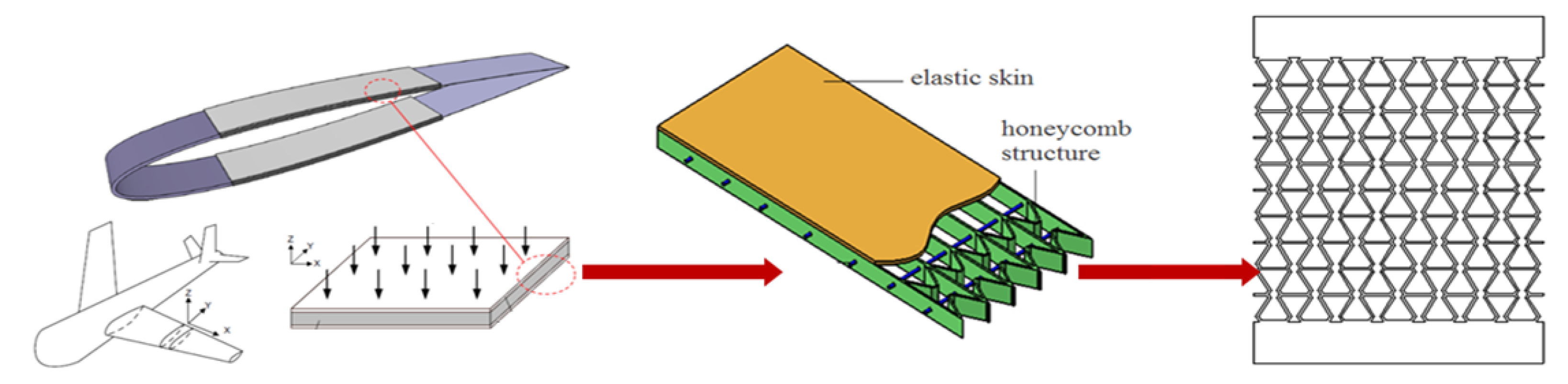
1. Introduction

Morphing aircraft is one of the important development directions for future aircraft. As a key component of such aircraft, morphing wings can alter their geometric shape in response to changes in external aerodynamic loads, optimizing aerodynamic performance across different mission profiles [1,2,3,4]. The flexible skin, an essential deformable component of the morphing wing surface, must not only have sufficient flexibility to enable smooth transitions between different airfoil shapes but also withstand aerodynamic loads during flight, playing a decisive role in the wing’s aerodynamic performance changes (as shown in Figure 1).

Among the various flexible skin designs, the composite flexible skin proposed by Olympio and Gandhi [5,6] shows promising application prospects. This skin uses a honeycomb structure as the core, covered with a thin elastic surface layer of low modulus and high strain. The elastic surface layer provides a smooth aerodynamic shape, while the honeycomb structure offers sufficient “out-of-plane” stiffness to bear aerodynamic loads. The flexible skin imposes high demands on the honeycomb structure, requiring high “in-plane” deformation capability and high “out-of-plane” stiffness.

Hexagonal honeycomb structures are the most common type of structure and offer a wide range of manufacturing methods and material options. However, when these honeycomb structures are stretched in one direction, they exhibit contraction in the orthogonal direction. Additionally, when subjected to bending loads, they may exhibit a “saddle-shaped” effect, which limits their application in flexible skins. Therefore, research on zero Poisson’s ratio and negative Poisson’s ratio honeycomb structures is continually being pursued.

Zero Poisson’s ratio honeycombs do not cause deformation in the orthogonal direction when deforming in one direction. Bubert et al. [7] from the University of Maryland designed and fabricated a deformable wing skin structure composed of zero Poisson’s ratio honeycombs and flexible skin, capable of achieving 100% tensile deformation but limited to one-dimensional deformation; Ai et al. [8] from the University of Bristol developed an optimization method for the in-plane stiffness of accordion zero Poisson’s ratio honeycombs; in 2020, Mohammad et al. [9,10] proposed a new fish cell structure with zero Poisson’s ratio effect in both orthogonal directions.

Compared to positive Poisson’s ratio honeycombs, negative Poisson’s ratio honeycombs generally possess higher in-plane shear flexibility and stronger compressive performance. These honeycombs include concave hexagonal honeycombs, chiral honeycombs [11], star-shaped honeycombs [12], double-arrow honeycombs [13], and other special concave honeycomb structures. Abderrezak Bezazi [14,15] and others used the energy method to calculate the equivalent elastic modulus of irregular polygonal honeycomb structures; Wenjun Dong et al. [16] derived analytical expressions for two orthogonal equivalent moduli and Poisson’s ratio for the “accordion” honeycomb structure using classical Euler beam theory; Yu-chao Guo et al. [17,18] studied the equivalent mechanical properties of a special concave polygonal honeycomb structure using theoretical and numerical simulation methods. However, the above studies generally use theoretical methods or numerical simulations, with limited research and comparison on the actual mechanical properties of negative Poisson’s ratio honeycombs in experiments.

In this paper, we conducted theoretical research on the in-plane and out-of-plane equivalent mechanical properties of a special concave honeycomb structure, deriving analytical formulas for its equivalent elastic modulus, equivalent shear model, and equivalent bending modulus. We used additive manufacturing methods, based on photosensitive resin materials, to manufacture a series of honeycomb structure test pieces, conducted mechanical performance tests on the honeycomb structures, and compared the theoretical values of the equivalent mechanical properties with the experimental values, providing support for the research of this type of honeycomb structure.

2. Introduction to Honeycomb Structure

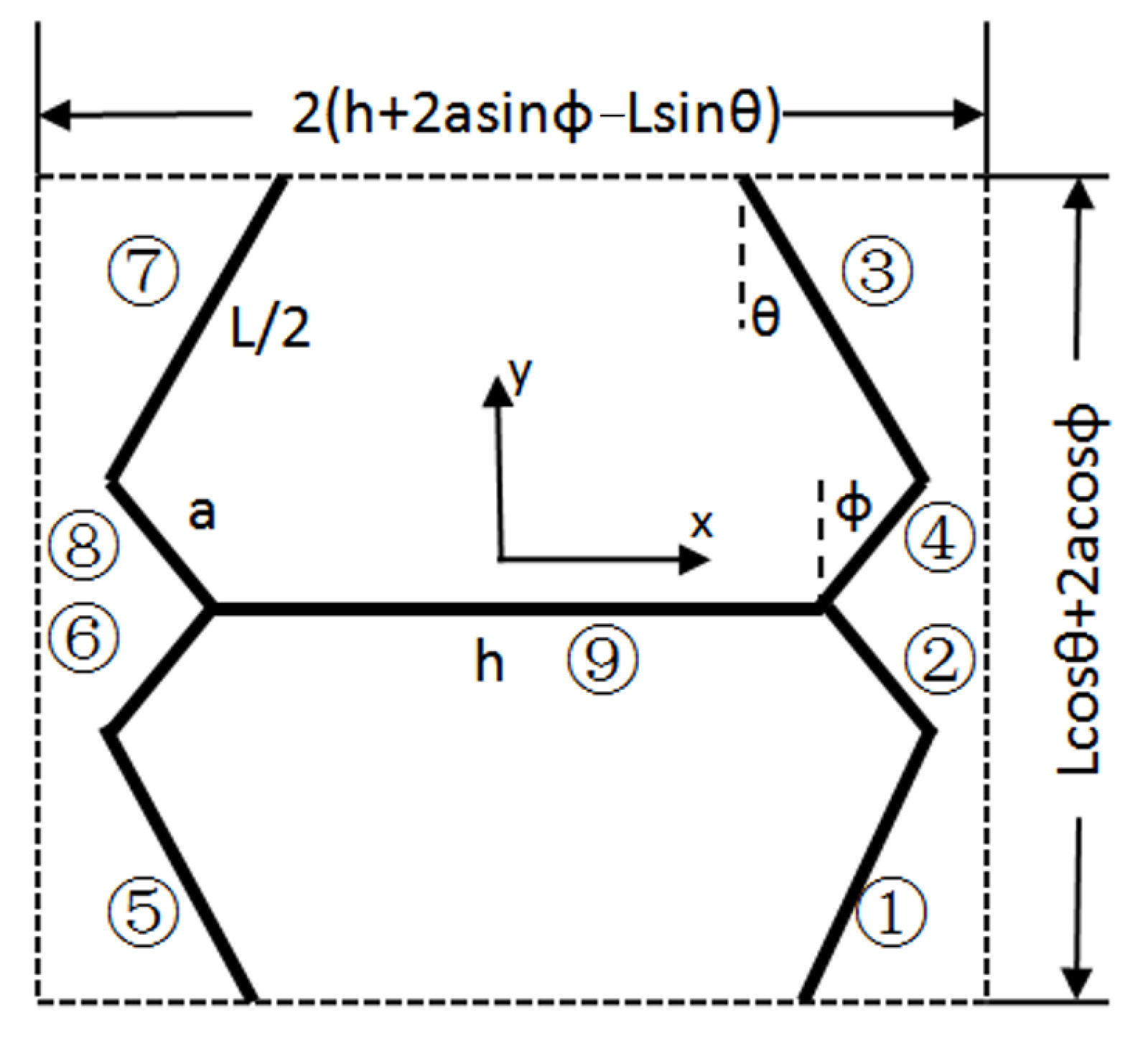
2.1. Geometric Parameters

As shown in Figure 2, the concave honeycomb structure has the following typical geometric parameters for the honeycomb cells: the length of the short inclined sides AB and CD is $a$, forming an angle $\varphi$ with the vertical direction, and the cell wall thickness is $t$; the length of the long inclined side BC is $L$, forming an angle $\theta$ with the vertical direction, and the thickness is $t$; the length of the horizontal sides EA and DF is $h/2$, and the cell wall thickness is $t$; the depth of the honeycomb is $b$.

2.2. Specimen

Using additive manufacturing technology, the honeycomb structure was fabricated with a photosensitive resin (SZUV-W8001). The mechanism of additive manufacturing involves using a liquid photosensitive resin that undergoes photopolymerization when exposed to ultraviolet (UV) laser light. Under computer control, the laser scans and solidifies the resin layer by layer according to the layered cross-sectional information of the part. The basic process is as follows: first, the build platform, controlled by the Z-axis, is positioned on the surface of the resin. The resin in the scanned area undergoes a photopolymerization reaction and solidifies, forming a cross-sectional layer of the part. After one layer is cured, the platform descends by a distance equal to the layer thickness while the resin level remains unchanged. The recoating process applies a new layer of liquid resin onto the previously cured cross-sectional layer. The computer then controls the laser to scan the next cross-sectional layer. This process repeats, layer by layer, tightly bonding each layer without any gaps until the entire part is formed. The final fabricated honeycomb structure test specimen is shown in Figure 3.

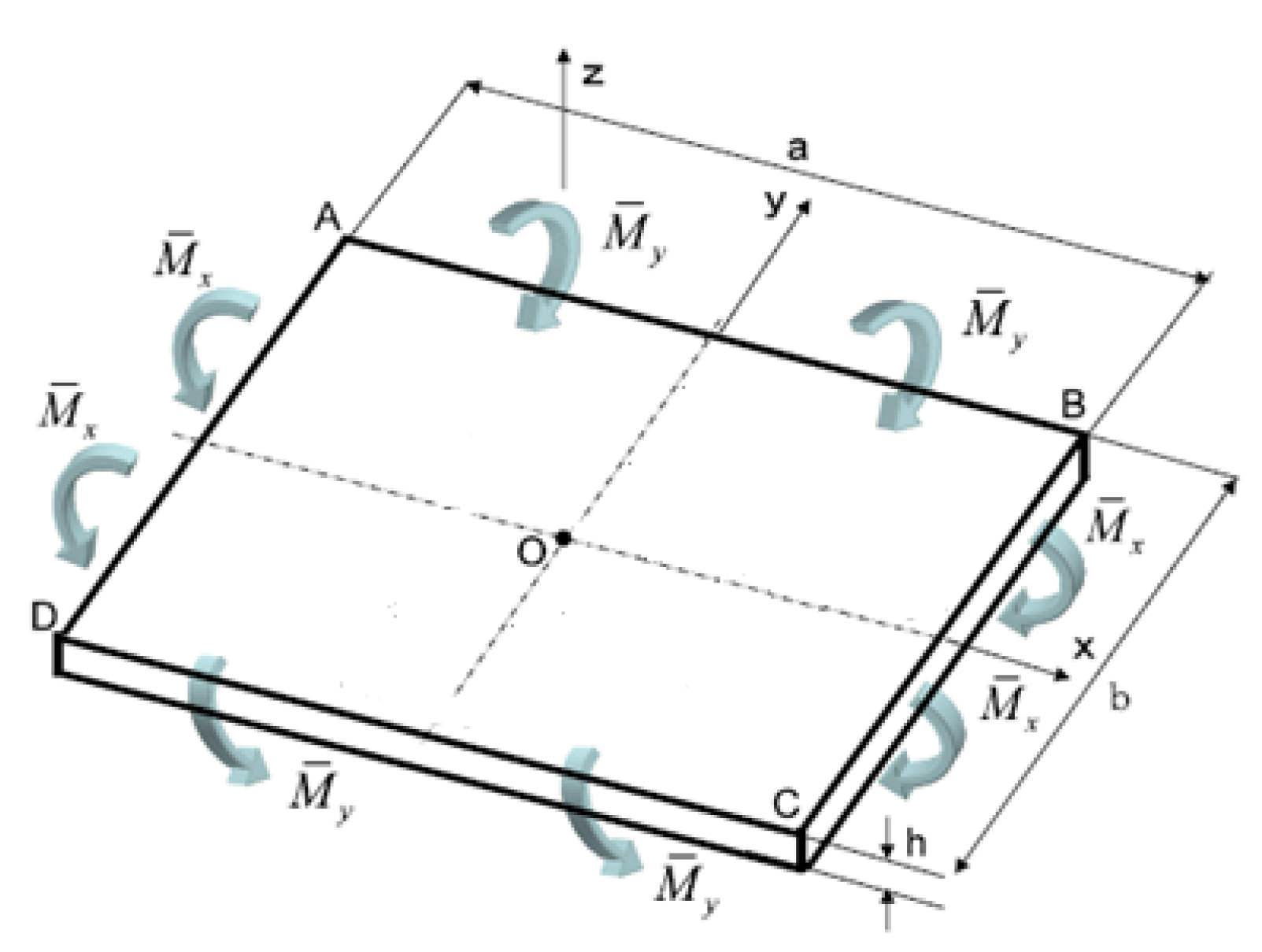
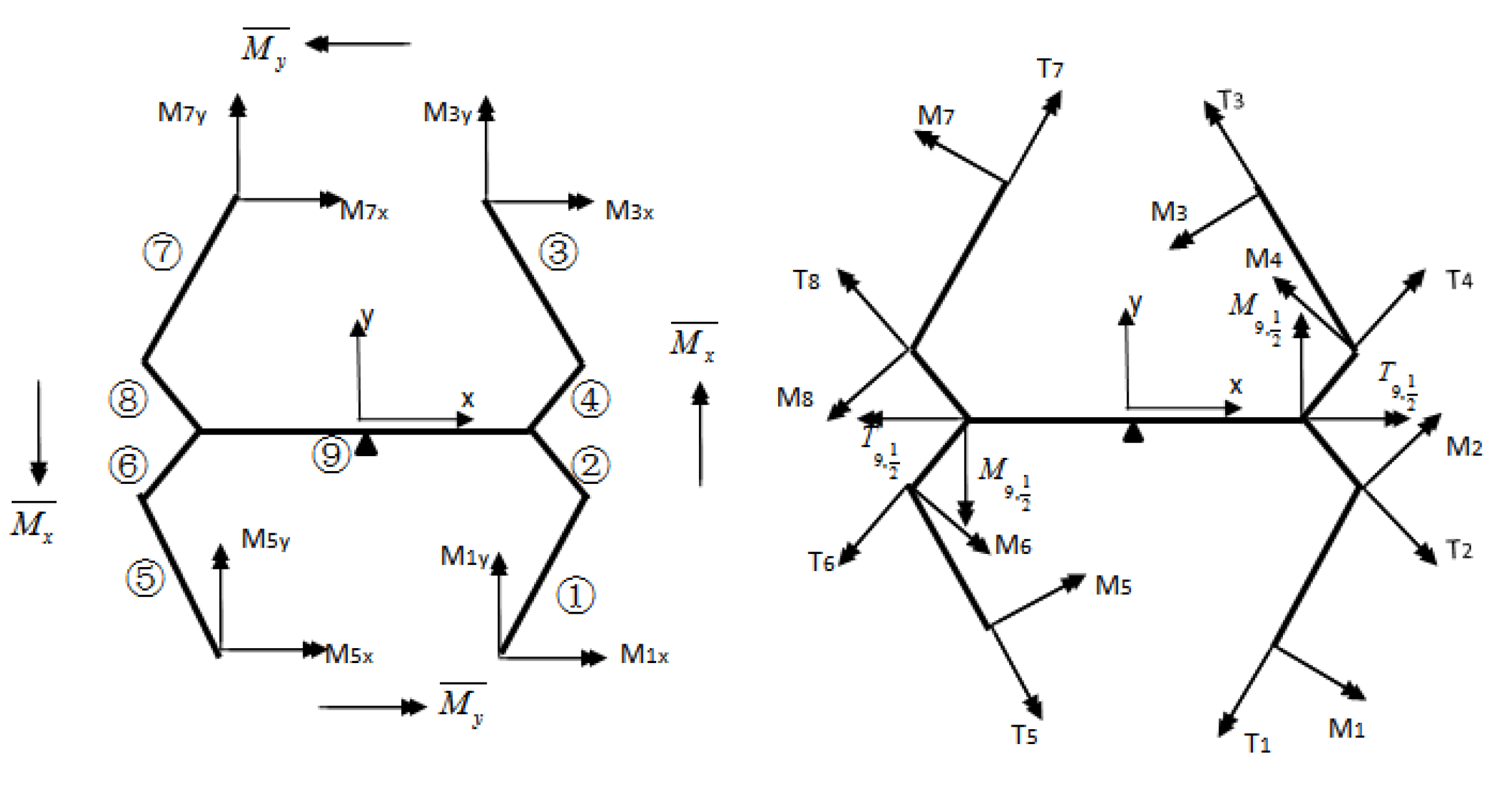
3. Theoretical Analysis of Mechanical Properties

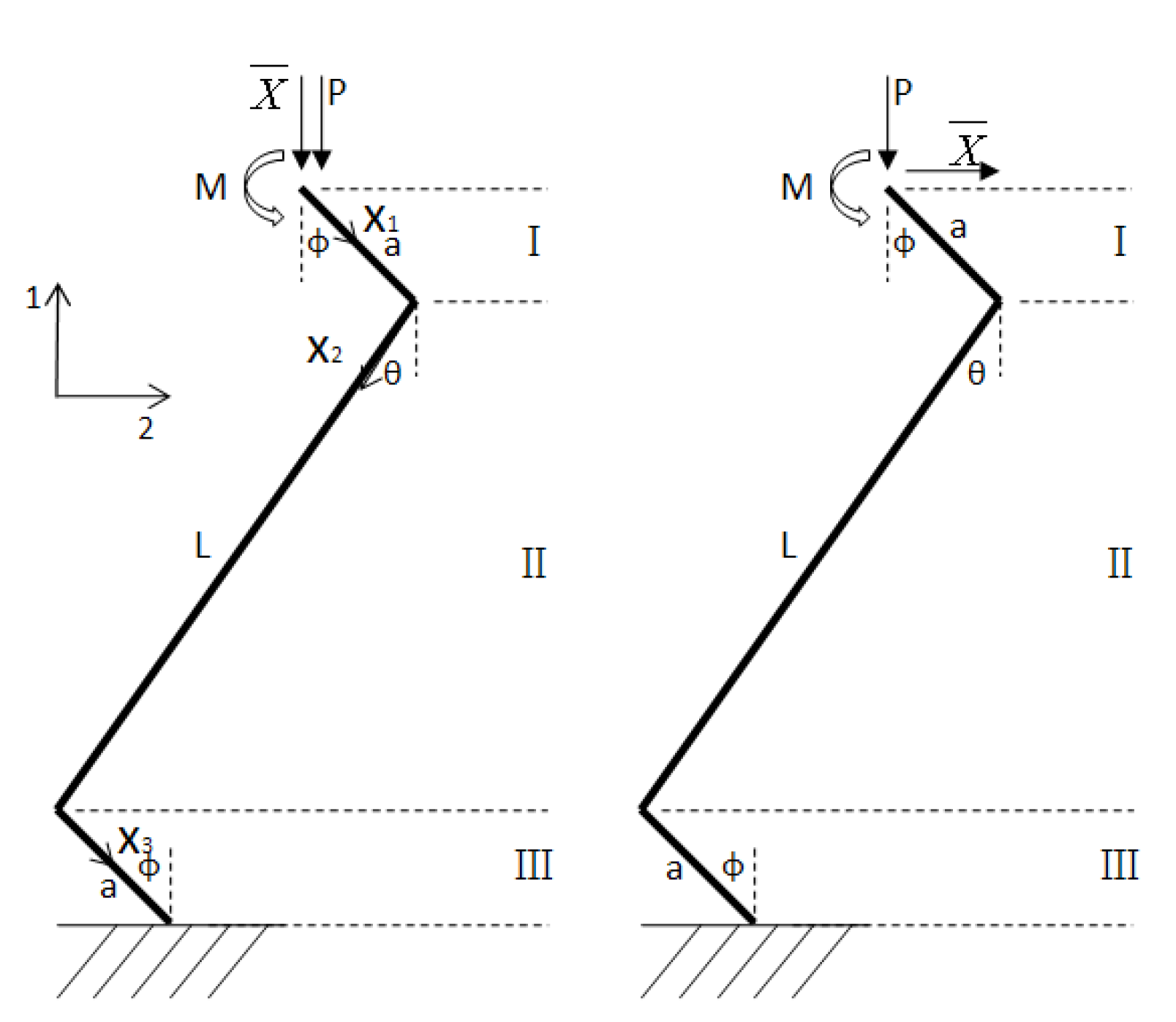
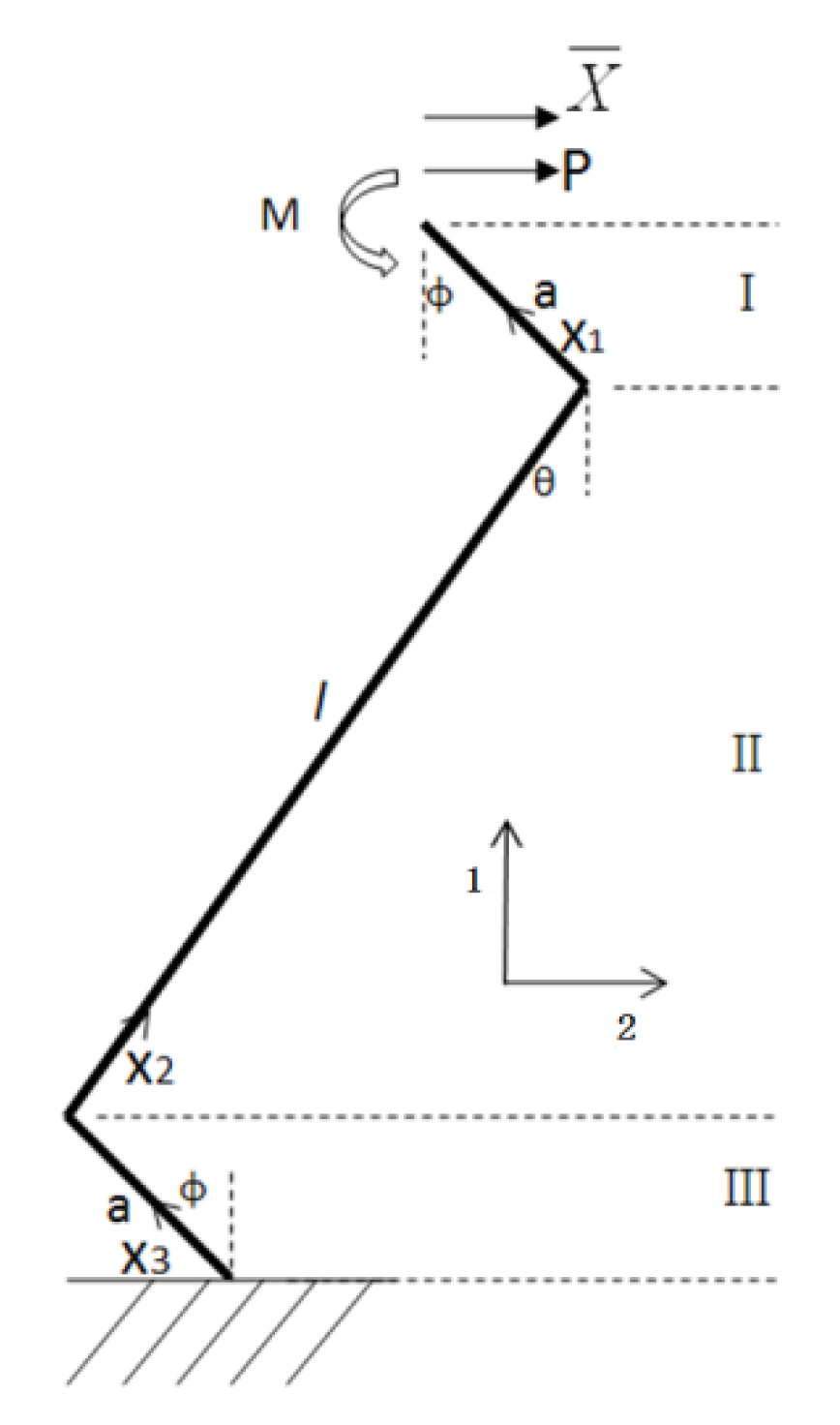
3.1. Equivalent Elastic Modulus

To analyze the equivalent elastic modulus of a quarter of the honeycomb cell, as shown in the dashed box in Figure 2, it should be noted that the cell wall thickness of the horizontal sides EA and DF should be $t/2$ when selecting a quarter of the honeycomb cell for analysis. The honeycomb cell wall is assumed to be a beam, with deformation components due to the moment, shear force, and axial compression from the axial force. Given that the shear deformation and axial deformation are relatively small, they can be neglected, focusing primarily on the deformation caused by bending moments. Additionally, the influence of the horizontal side $h$ on the deformation of the honeycomb structure is minimal and can be simplified in theoretical analysis, as shown in Figure 4.

First, calculate the equivalent elastic modulus in the 1-direction of the honeycomb core material. For convenience, the honeycomb cell wall is divided into segments I, II, and III, each with its own local coordinate system. Assuming no torsional deformation at the loading end, calculate the additional moment $M=P(L\sin \theta -2a\sin \varphi )/2$ at the loading end. With this moment $M$ and the concentrated load $P$ at the end, the moments in segments I, II, and III are computed.

$$\left\{\begin{array}{ll}{M}_{\mathrm{I}}=M+P{x}_1\sin \varphi & (0\le x_1\le a)\\ M_{\mathrm{II}}=M+P\mathrm{a}\sin \varphi -P{x}_2\sin \theta & (0\le x_2\le L)\\ M_{\mathrm{III}}=M+P\mathrm{a}\sin \varphi -PL\sin \theta +P{x}_3\sin \varphi & (0\le x_3\le a)\end{array}\right.$$

(1)

Simultaneously, calculate the moment under a unit load $\overline{X}=1$ in the direction of the required displacement, with the results as follows:

$$\left\{\begin{array}{ll}\overline{M_{\mathrm{I}}}=x_1\sin \varphi & (0\le x_1\le a)\\ \overline{M_{\mathrm{II}}}=\mathrm{a}\sin \varphi -x_2\sin \theta & (0\le x_2\le L)\\ \overline{M_{\mathrm{III}}}=\mathrm{a}\sin \varphi -L\sin \theta +x_3\sin \varphi & (0\le x_3\le a)\end{array}\right.$$

(2)

The deformation of the honeycomb cell wall in the 1-direction under the load $P$ is obtained:

$$\begin{array}{c}{\delta }_1={\displaystyle \sum _e{\displaystyle \underset{0}{\overset{l}{\int }}}\frac{\overline{M}{M}_P}{EI}ds}\hfill \\ \hspace{1em}={\displaystyle \frac{1}{2E_{s}I}}(P{L}^{2}a{\sin }^2\theta +{\displaystyle \frac{4P{a}^3{\sin }^2\varphi }{3}}-2PL{a}^2\sin \theta \sin \varphi +{\displaystyle \frac{P{L}^3{\sin }^2\theta }{6}})\hfill \end{array}$$

(3)

where $I=b{t}^3/12$ is the moment of inertia of the honeycomb cell wall, $t$ is the thickness of the honeycomb cell wall, $b$ is the depth of the honeycomb core, and $M_P$ is the actual moment within the structure under the load $P$.

The strain in the 1-direction can be calculated based on the deformation of the honeycomb cell wall:

$${\epsilon }_1={\displaystyle \frac{{\delta }_1}{L\cos \theta +2a\cos \varphi }}$$

(4)

where ${\delta }_1$ is as shown in Equation (3).

From the overall force balance, it can be determined that:

$${\sigma }_1={\displaystyle \frac{P}{b(h+2a\sin \varphi -L\sin \theta )}}$$

(5)

The equivalent elastic modulus $E_1$ in the 1-direction of the honeycomb core material can be determined by the following equation $E_1={\sigma }_1/{\epsilon }_1$, eliminating the influence of the honeycomb material $E_s$:

$${\displaystyle \frac{E_1}{E_s}}={\displaystyle \frac{t^3(L\cos \theta +2 a\cos \varphi )}{(h+2a\sin \varphi -L\sin \theta )}}\times {\displaystyle \frac{1}{(6L^{2}a {\sin }^2\theta +8a^3{\sin }^2\varphi -12L{a}^2 \sin \theta \sin \varphi +L^3{\sin }^2\theta )}}$$

(6)

where $E_s$ is the elastic modulus of the honeycomb material.

Similarly, the equivalent elastic modulus in the 2-direction can be calculated.

$${\displaystyle \frac{E_2}{E_s}}={\displaystyle \frac{t^3(h+2a\sin \varphi -L\sin \theta )}{(L\cos \theta +2a\cos \varphi )}}\times {\displaystyle \frac{1}{(6L^{2}a {\cos }^2\theta +8a^3 {\cos }^2\varphi +12L{a}^2\cos \theta \cos \varphi +L^3 {\cos }^2 \theta )}}$$

(7)

3.2. Equivalent Shear Modulus

Considering the symmetry of the honeycomb cell, to simplify the calculation process, a quarter of the honeycomb cell is taken and the cell walls are simplified as beams to calculate the deformation under transverse (2-direction) loading. Due to the transverse (2-direction) loading, the cell walls AE and DF primarily undergo axial deformation, which has minimal impact on the overall transverse deformation of the structure and can be neglected. Thus, the simplified calculation model is shown in Figure 5.

Using a similar method to calculate the equivalent elastic modulus, the equivalent in-plane shear modulus of the honeycomb can be obtained as follows:

$$\begin{array}{c}{\displaystyle \frac{G_{12}}{E_s}}={\displaystyle \frac{\tau }{\gamma E_s}}\hfill \\ \hspace{1em}\hspace{1em}={\displaystyle \frac{t^3(l\cos \theta +2a\cos \varphi )}{(h+2a\sin \varphi -l\sin \theta )}}\times {\displaystyle \frac{1}{(6l^{2}a{\cos }^2 \theta +8a^3 {\cos }^2 \varphi +12l{a}^2 \cos \theta \cos \varphi +l^3 {\cos }^2 \theta )}}\hfill \end{array}$$

(8)

where $E_s$ is the elastic modulus of the honeycomb material.

3.3. Equivalent Bending Stiffness

To facilitate the study of the equivalent bending stiffness of the honeycomb structure, an appropriate cell structure is first selected, as shown in Figure 6. The geometric parameters of the honeycomb cell are as follows: the length of the long diagonal edge is $L/2$ and the angle with the vertical direction is $\theta$; the length of the short diagonal edge is $a$, and the angle with the vertical direction is $\varphi$; the length of the horizontal edge at the center of the cell is $h$; the width of the honeycomb cell is $2(h+2a\sin \varphi -L\sin \theta )$; the height of the honeycomb cell is $L\cos \theta +2a\cos \varphi$; the depth of the honeycomb cell is $c$; the thickness of the honeycomb cell wall is $t$; the elastic modulus of the honeycomb material is $E_s$. The numbering of each cell wall of the honeycomb cell is as shown in Figure 6.

The honeycomb cell structure is equivalently transformed into an orthotropic thin plate (as shown in Figure 7), and then the deformation energy of the thin plate can be obtained using the deformation energy formula.

The deformation energy of an orthotropic thin plate is:

$$u_e={\displaystyle \frac{2\alpha \gamma D_{22}}{D_{11}{D}_{22}-D_{12}^2}}{\overline{M_x}}^2-{\displaystyle \frac{4\alpha \gamma D_{12}}{D_{11}{D}_{22}-D_{12}^2}}\overline{M_x}\overline{M_y}+{\displaystyle \frac{2\alpha \gamma D_{11}}{D_{11}{D}_{22}-D_{12}^2}}{\overline{M_y}}^2$$

(9)

where $\alpha =h+2a\sin \varphi -L\sin \theta$, $\gamma =(L\cos \theta +2a\cos \varphi )/2$.

First, assume that the honeycomb cell is subjected to uniformly distributed bending moments $\overline{M_x}$ and $\overline{M_y}$, with the center point of the cell as the support point. Using the load balance conditions, the moments and torques in the global coordinate system and the local coordinate system of each cell wall can be obtained (as shown in Figure 8).

Under the uniformly distributed bending moments $\overline{M_x}$ and $\overline{M_y}$, the moments and torques on each cell wall are:

$$\left\{\begin{array}{l}{M}_1=M_{1x}\cos \theta -M_{1y}\sin \theta \\ T_1=-M_{1x}\sin \theta -M_{1y}\cos \theta \\ M_2=M_{1x}\cos \varphi +M_{1y}\sin \varphi \\ T_2=M_{1x}\sin \varphi -M_{1y}\cos \varphi \\ M_{9,{\displaystyle \frac{1}{2}}}=M_{1y}+M_{3y}\\ T_{{}_{9,{\displaystyle \frac{1}{2}}}}=M_{1x}+M_{3x}\end{array}\right.$$

(10)

Due to the symmetry of the honeycomb structure, the moments caused by $\overline{M_x}$ on cell walls 1 and 5, and cell walls 3 and 7 are equal, and the moments caused by $\overline{M_y}$ on cell walls 1 and 3, and cell walls 5 and 7 are equal. Therefore, we have:

$$\left\{\begin{array}{l}{M}_{1x}=\alpha \overline{M_y}\\ M_{1y}=\gamma \overline{M_x}\\ M_{3x}=-\alpha \overline{M_y}\\ M_{3y}=\gamma \overline{M_x}\end{array}\right.$$

(11)

the meanings of $\alpha$ and $\gamma$ are consistent with those mentioned previously.

The deformation energy of a single cell wall can be expressed as:

$$u_i={\displaystyle \frac{1}{2}}M{\theta }_M+{\displaystyle \frac{1}{2}}T{\theta }_T$$

(12)

where ${\theta }_M$ and ${\theta }_T$ are the torsional angles of a single cell wall under the action of moments $M$ and torques $T$, which can be calculated based on the theoretical deformation formulas of cantilever thin plates [19].

The deformation energy of cell wall 1 under the action of moment $M_1$ and torque $T_1$ is:

$$\begin{array}{c}{u}_1={\overline{M_x}}^2({\displaystyle \frac{3L{\gamma }^2 {\sin }^2 \theta }{E_s{t}_s{c}^3}}+{\displaystyle \frac{3L^2{q}_L{\gamma }^2{\cos }^2\theta }{2E_s{t}_s{}^3{c}^2}})+{\overline{M_y}}^2({\displaystyle \frac{3L{\alpha }^2 {\cos }^2 \theta }{E_s{t}_s{c}^3}}+{\displaystyle \frac{3L^2{q}_L{\alpha }^2 {\sin }^2\theta }{2E_s{t}_s{}^3{c}^2}})\hfill \\ \hspace{1em}+\overline{M_x}\overline{M_y}({\displaystyle \frac{3L^2{q}_L\alpha \gamma \sin 2\theta }{2E_s{t}_s{}^3{c}^2}}-{\displaystyle \frac{3L\alpha \gamma \sin 2\theta }{E_s{t}_s{c}^3}})\hfill \end{array}$$

(13)

Similarly, the deformation energy of cell wall 2 under the action of moment $M_2$ and torque $T_2$ is:

$$\begin{array}{c}{u}_2={\overline{M_x}}^2({\displaystyle \frac{6a{\gamma }^2 {\sin }^2 \varphi }{E_s{t}_s{c}^3}}+{\displaystyle \frac{6a^2{q}_a{\gamma }^2 {\cos }^2 \varphi }{E_s{t}_s{}^3{c}^2}})+{\overline{M_y}}^2({\displaystyle \frac{6a{\alpha }^2 {\cos }^2 \varphi }{E_s{t}_s{c}^3}}+{\displaystyle \frac{6a^2{q}_a{\alpha }^2 {\sin }^2 \varphi }{E_s{t}_s{}^3{c}^2}})\hfill \\ \hspace{1em}+\overline{M_x}\overline{M_y}({\displaystyle \frac{6a\alpha \gamma \sin 2\varphi }{E_s{t}_s{c}^3}}-{\displaystyle \frac{6a^2{q}_a\alpha \gamma \sin 2\varphi }{E_s{t}_s{}^3{c}^2}})\hfill \end{array}$$

(14)

Likewise, the deformation energy of the right side of the center constraint point of cell wall 9 under the action of moment $M_9$ and torque $T_9$ is:

$$u_{9,{\displaystyle \frac{1}{2}}}={\displaystyle \frac{12\mathrm{h}{\gamma }^2{\overline{M_x}}^2}{E_s{t}_s{c}^3}}$$

(15)

Due to the symmetry of the structure and loading, when subjected to moments, the deformation energies of cell walls 1, 3, 5, and 7 are equal, and the deformation energies of cell walls 2, 4, 6, and 8 are equal. Therefore, the total strain energy of the honeycomb cell walls is:

$$u_a=4(u_1+u_2)+2u_{9,{\displaystyle \frac{1}{2}}}$$

(16)

Using the equivalence of deformation energies $u_a=u_e$, and matching the corresponding coefficients $D_{11}$, $D_{22}$ and $D_{12}$ in Equations (9) and (16), the bending stiffness of the structure can be obtained as:

$$\left\{\begin{array}{l}{D}_{11}={\displaystyle \frac{\mathrm{B}}{AB-C^2}}\\ D_{22}={\displaystyle \frac{\mathrm{A}}{AB-C^2}}\\ D_{12}={\displaystyle \frac{\mathrm{C}}{AB-C^2}}\end{array}\right.$$

(17)

where:

$$A={\displaystyle \frac{6L\gamma {\sin }^2 \theta }{E_s{t}_s{c}^3 \alpha }}+{\displaystyle \frac{6L^2{q}_L \gamma {\cos }^2 \theta }{2E_s{t}_s{}^3{c}^2 \alpha }}+{\displaystyle \frac{12a\gamma {\sin }^2 \varphi }{E_s{t}_s{c}^3 \alpha }}+{\displaystyle \frac{12a^2{q}_a\gamma {\cos }^2 \varphi }{E_s{t}_s{}^3{c}^2 \alpha }}+{\displaystyle \frac{12\mathrm{h}\gamma }{E_s{t}_s{c}^3 \alpha }}$$

$$B={\displaystyle \frac{6L\alpha {\cos }^2 \theta }{E_s{t}_s{c}^3 \gamma }}+{\displaystyle \frac{6L^2{q}_L\alpha {\sin }^2 \theta }{2E_s{t}_s{}^3{c}^2 \gamma }}+{\displaystyle \frac{12a\alpha {\cos }^2 \varphi }{E_s{t}_s{c}^3 \gamma }}+{\displaystyle \frac{12a^2 q_a\alpha {\sin }^2 \varphi }{E_s{t}_s{}^3{c}^2 \gamma }}$$

$$C=-{\displaystyle \frac{3L^2{q}_L \sin 2\theta }{2E_s{t}_s{}^3{c}^2}}+{\displaystyle \frac{3L \sin 2\theta }{E_s{t}_s{c}^3}}-{\displaystyle \frac{6a \sin 2\varphi }{E_s{t}_s{c}^3}}+{\displaystyle \frac{6a^2{q}_a \sin 2\varphi }{E_s{t}_s{}^3{c}^2}}$$

4. Mechanical Properties Testing

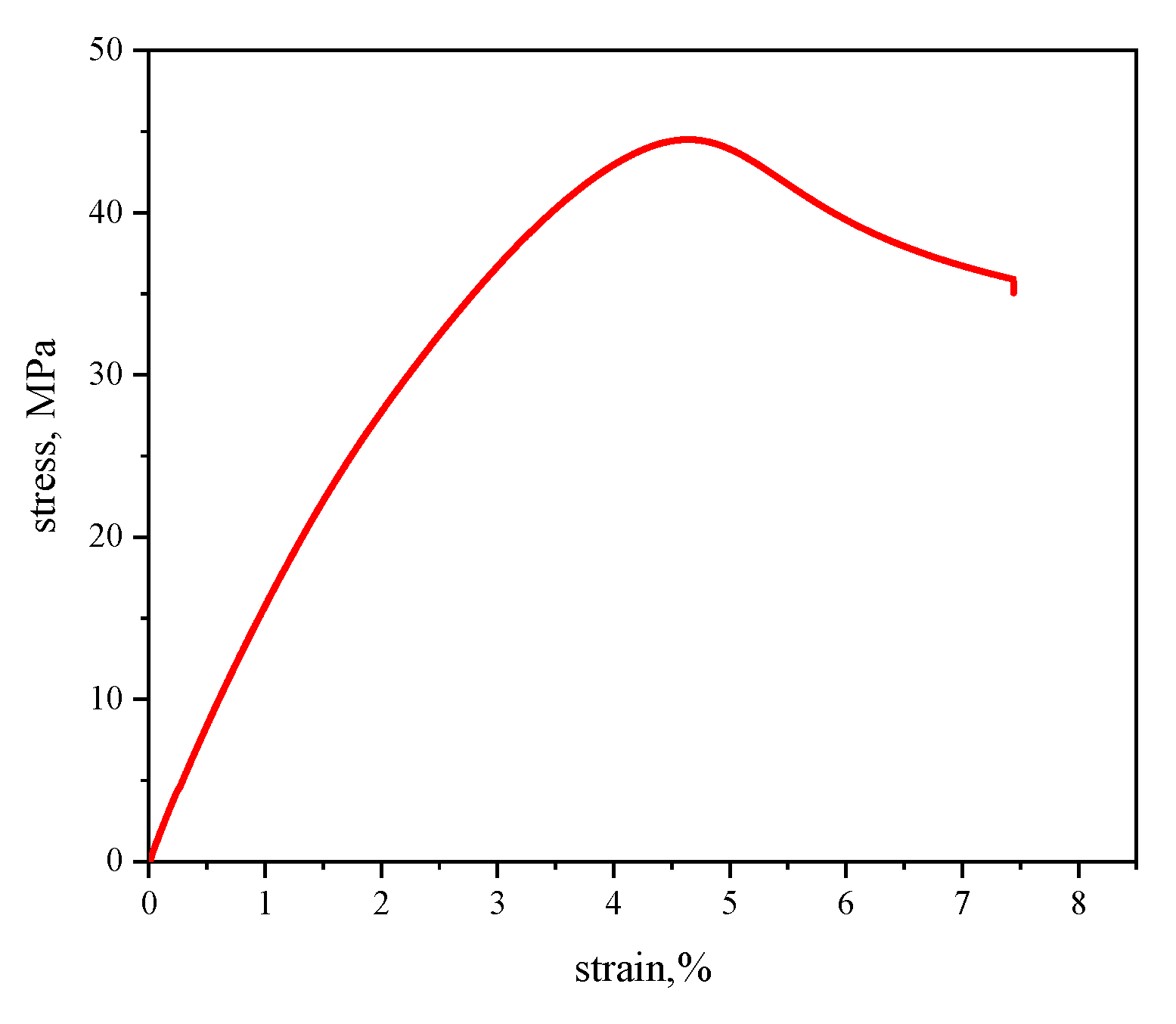
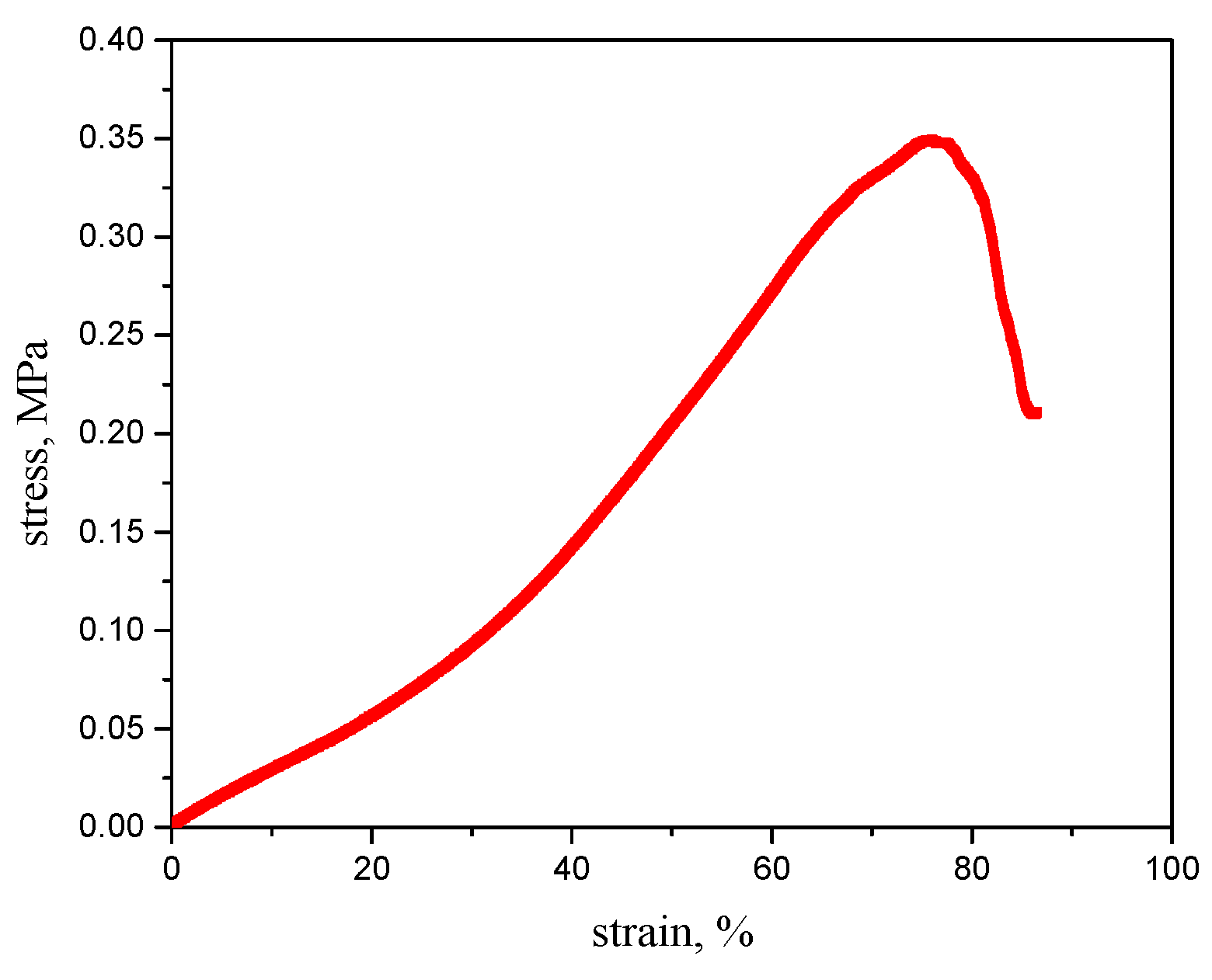
4.1. Material Properties Testing

To determine the mechanical properties of the photosensitive resin, typical test specimens were prepared according to the ASTM D638-08 standard. Tensile tests were conducted using an Instron 5566 universal testing machine with a load capacity of 10 kN and a tensile speed of 10 mm/s. The test specimens were fabricated using the same photo-curing laser rapid prototyping technology.

The tensile stress–strain curve of the photosensitive resin obtained from the tensile test is shown in Figure 9. From the curve, the mechanical properties of the photosensitive resin are as follows: The elastic modulus of the photosensitive resin is approximately 1770 MPa, the tensile strength is 46.3 MPa, and the elongation at fracture is 7.5%, with the elastic deformation accounting for about 3%.

4.2. Elastic Modulus Testing of Honeycomb Structure

The mechanical testing of the honeycomb structure includes tensile, shear, and bending tests, all performed using a universal testing machine with a 10-kN load capacity. The equivalent elastic modulus of the honeycomb structure can be estimated from the slope of the linear segment of the measured stress–strain curve.

The tensile test of the honeycomb structure is shown in Figure 10. As the load increases, the honeycomb structure exhibits expansion in the orthogonal direction of the load, indicating a significant negative Poisson’s ratio characteristic. The tensile stress–strain curve of the honeycomb structure is shown in Figure 11. From the curve, it can be seen that the honeycomb structure exhibits good linearity within a 6% deformation range, with an elongation at fracture of 8.7%. Using the linear segment of the stress–strain curve, the elastic modulus of the honeycomb structure is calculated to be approximately 14.85 MPa. The elastic modulus calculated using theoretical formulas is 14.2 MPa, with a discrepancy of 4.38% between the theoretical and experimental results.

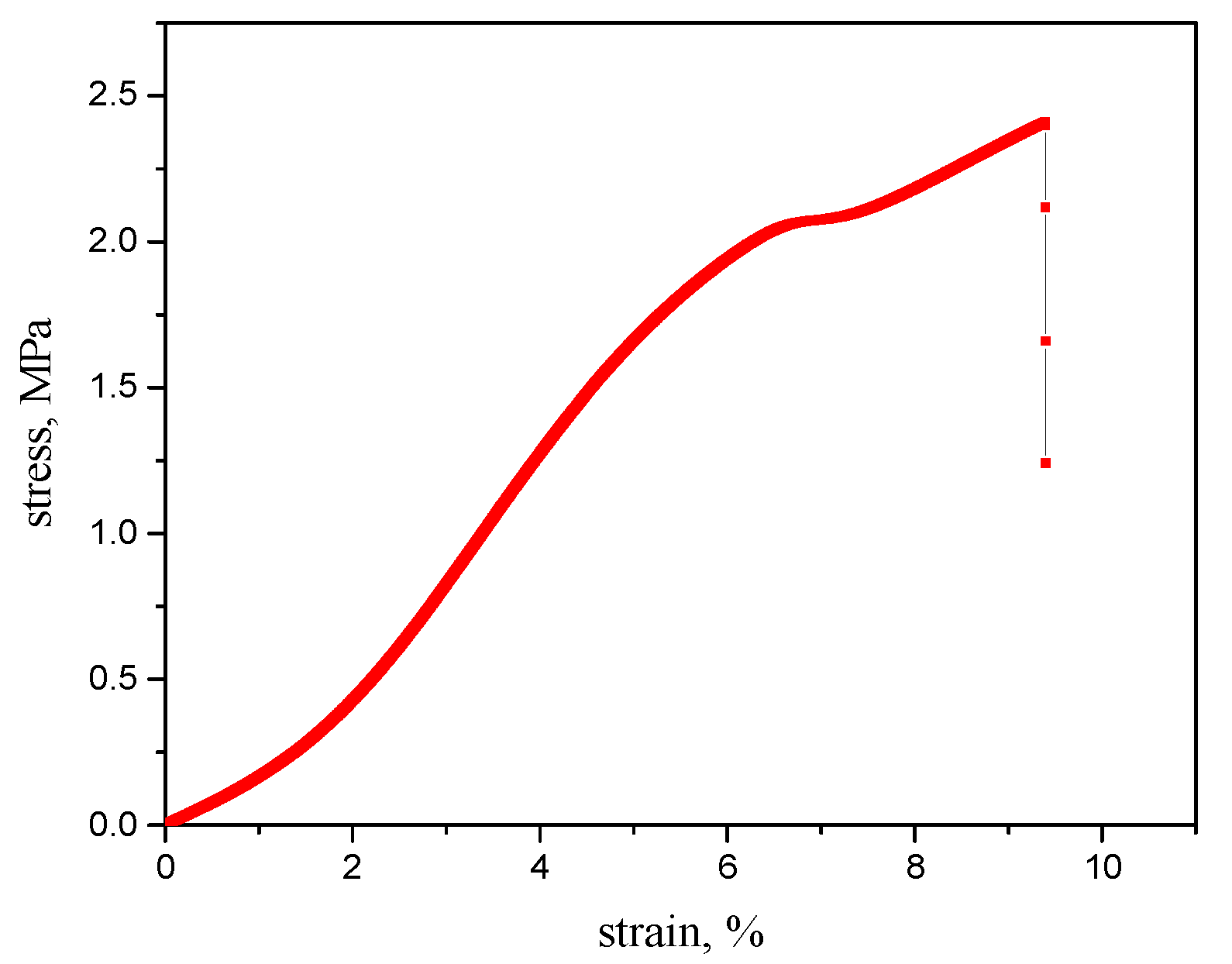
4.3. Shear Modulus Testing of Honeycomb Structure

The shear test of the honeycomb structure is shown in Figure 12. To accurately measure the shear modulus of the honeycomb structure, small-sized specimens were used to both apply the shear force and reduce the influence of bending moments on the test results. The equivalent shear modulus estimation method for the honeycomb structure is similar to the equivalent elastic modulus estimation method and can be calculated from the slope of the elastic segment of the measured stress–strain curve.

The shear stress–strain curve of the honeycomb structure is shown in Figure 13. From the curve, it can be seen that the honeycomb structure exhibits good linearity within a 30% deformation range, with a deformation rate at fracture of 85%. Using the linear segment of the stress–strain curve, the shear modulus of the honeycomb structure is calculated to be approximately 0.18 MPa. The shear modulus calculated using theoretical formulas is 0.15 MPa, with a discrepancy of 16.67% between the theoretical and experimental results.

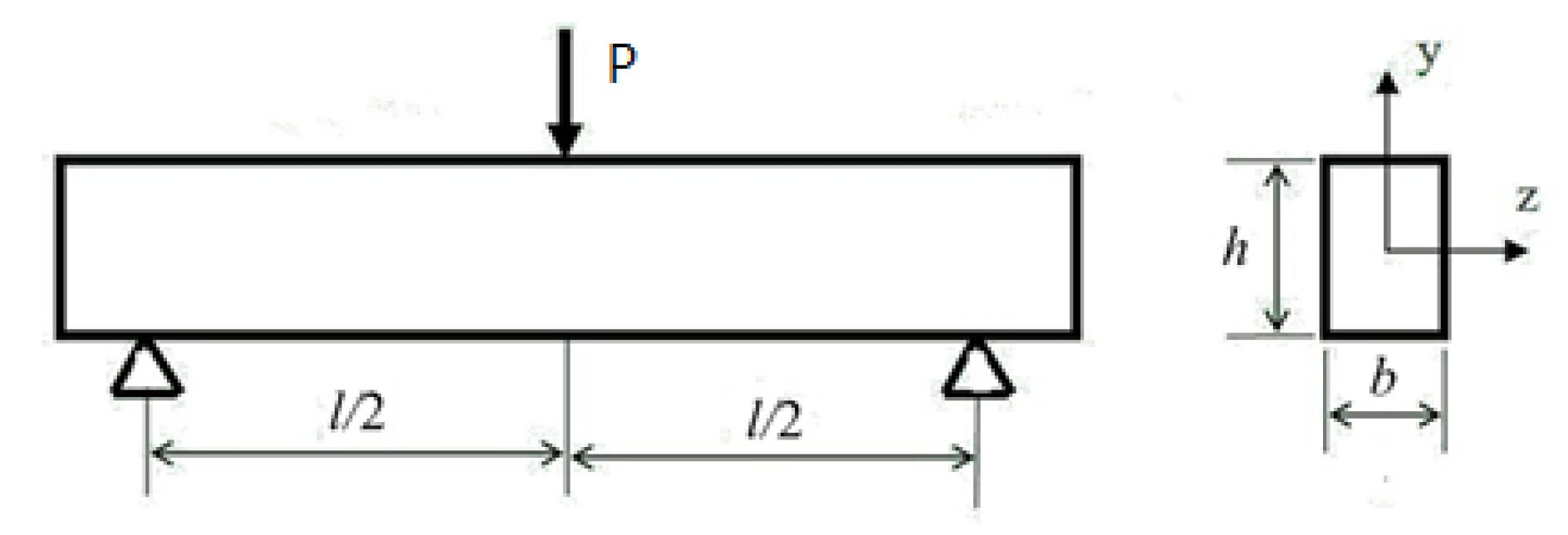
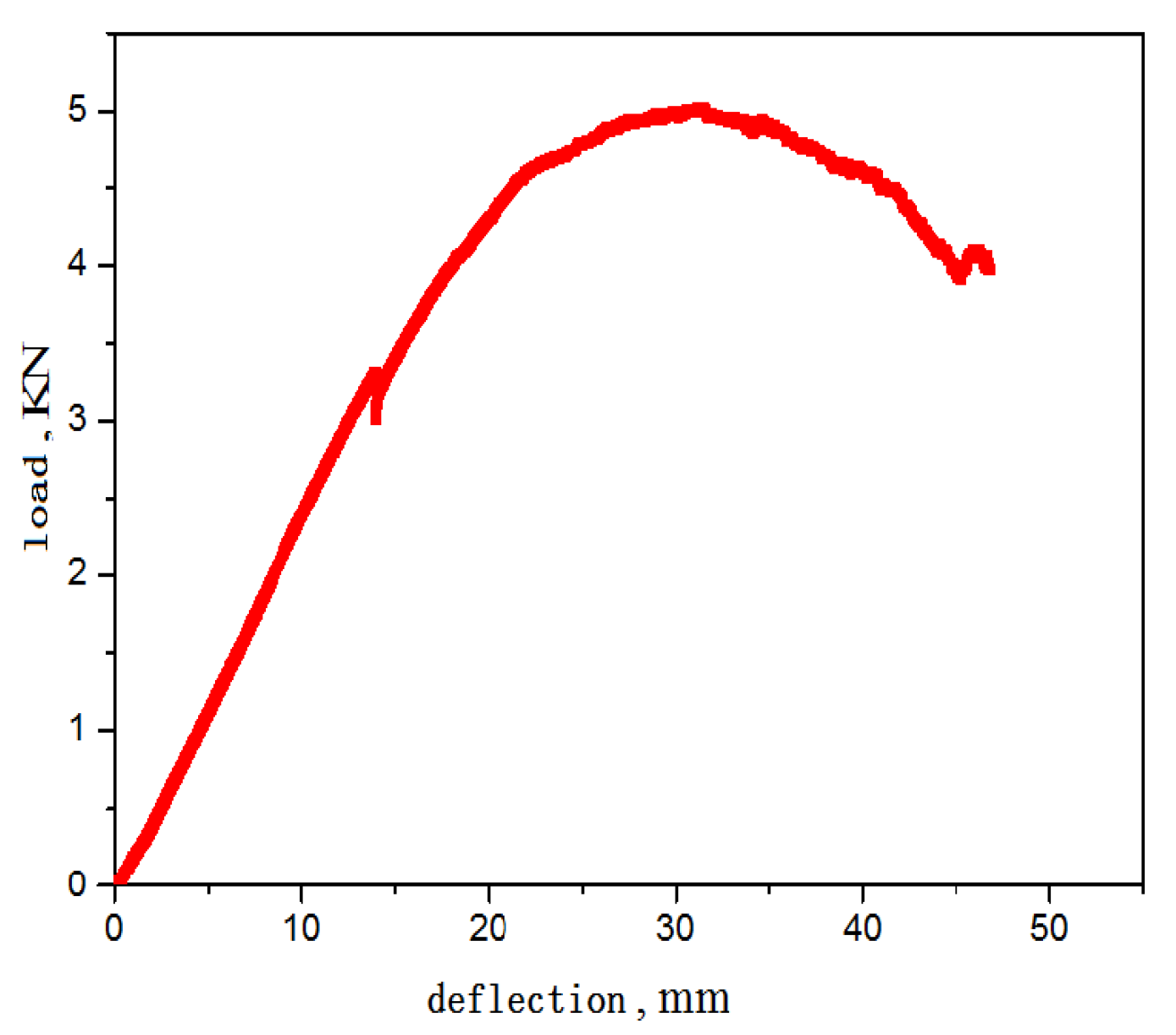
4.4. Bending Modulus Testing of Honeycomb Structure

The bending performance test of the honeycomb structure uses the three-point bending test method, with the three-point bending test model shown in Figure 14. The span between the two supports is $l$, with a concentrated load $P$ applied on top, a section width $b$, and a height $h$. For small deformations, the displacement measured by the sensor is approximately considered as the deflection $f$.

Based on the load-deflection curve obtained from the experiment, the equivalent bending modulus of the honeycomb structure can be estimated using the following calculation method:

$$E_b={\displaystyle \frac{l^3}{4b{h}^3}}\times {\displaystyle \frac{\mathrm{\Delta }P}{\mathrm{\Delta }f}}$$

(18)

where $\mathrm{\Delta }P$ is the load increment in the linear segment of the load-deflection curve, and $\mathrm{\Delta }f$ is the deflection increment in the linear segment of the load-deflection curve.

The bending test of the honeycomb structure is shown in Figure 15. By measuring the deflection of the honeycomb structure through the three-point bending test, its bending modulus is calculated. During the test loading process, the honeycomb structure does not exhibit saddle effects when subjected to out-of-plane bending loads, demonstrating a significant negative Poisson’s ratio characteristic.

The load-deflection curve of the honeycomb structure is shown in Figure 16. From the curve, it can be seen that the honeycomb structure exhibits good linearity within a 30% deformation range, with a deformation rate at fracture of 47%. Using the linear segment of the load-deflection curve, the bending modulus of the honeycomb structure is calculated to be approximately 7.63 MPa. The bending modulus calculated using theoretical formulas is 6.45 MPa, with a discrepancy of 15.47% between the theoretical and experimental results.

5. Discussion & Conclusions

This paper focused on a special concave honeycomb structure. First, specific cell units were selected, and their cell walls were simplified as beams. Using the principle of virtual work, the equivalent elastic modulus and shear modulus were derived. Next, specific cell units were selected and simplified as orthotropic thin plates. Using the principle of equivalent deformation energy, the equivalent bending stiffness was derived. Using additive manufacturing methods, a series of honeycomb structure test specimens were fabricated. The mechanical performance tests of the honeycomb structures were conducted, and the equivalent elastic modulus, shear modulus, and bending modulus of the honeycomb structures were calculated using the stress–strain or load-deflection curves obtained from the tests. The theoretical values of the equivalent mechanical properties were compared with the experimental values. The results show that the discrepancy between the theoretical and experimental values is 4.38% for the equivalent elastic modulus, 16.67% for the equivalent shear modulus, and 15.47% for the equivalent bending modulus, indicating small errors. The method provided in this paper can support the study of such honeycomb structures.

Furthermore, the main reasons for the discrepancy between the theoretical and experimental values are:

(1)

The theoretical method for calculating the elastic modulus of the honeycomb structure is based on the small deformation assumption and assumes that all structures are in a linear elastic deformation state, not considering material and geometric nonlinear effects.

(2)

Photosensitive materials are not linear elastic materials, and there is a certain error in the elastic modulus obtained from their stress–strain curves.

(3)

The stress–strain or load-deflection curves from the tests exhibit significant nonlinear effects. Using only the approximate linear segment for calculating the equivalent elastic modulus introduces some error.

(4)

The number of test specimens in this experiment was relatively small, resulting in some uncertainty in the results.

(5)

In summary, the above are the reasons for the discrepancy between the theoretical and experimental values, and further research can be conducted to address this issue.