Design Optimization and Testing of Seamless Morphing Leading Edge for Large Civil Aircraft †
Abstract
1. Introduction
2. Reference Aircraft and Structural Concept
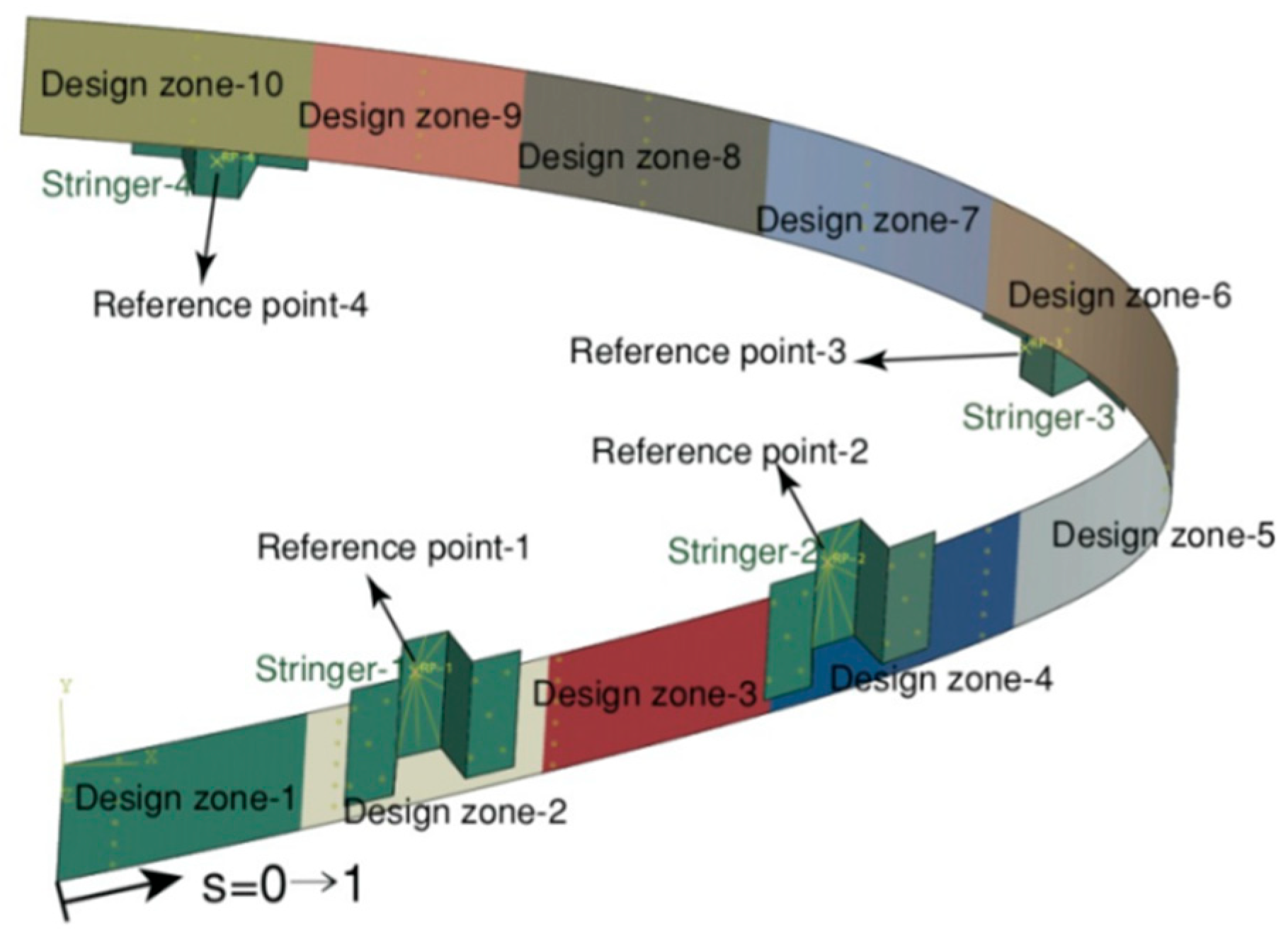
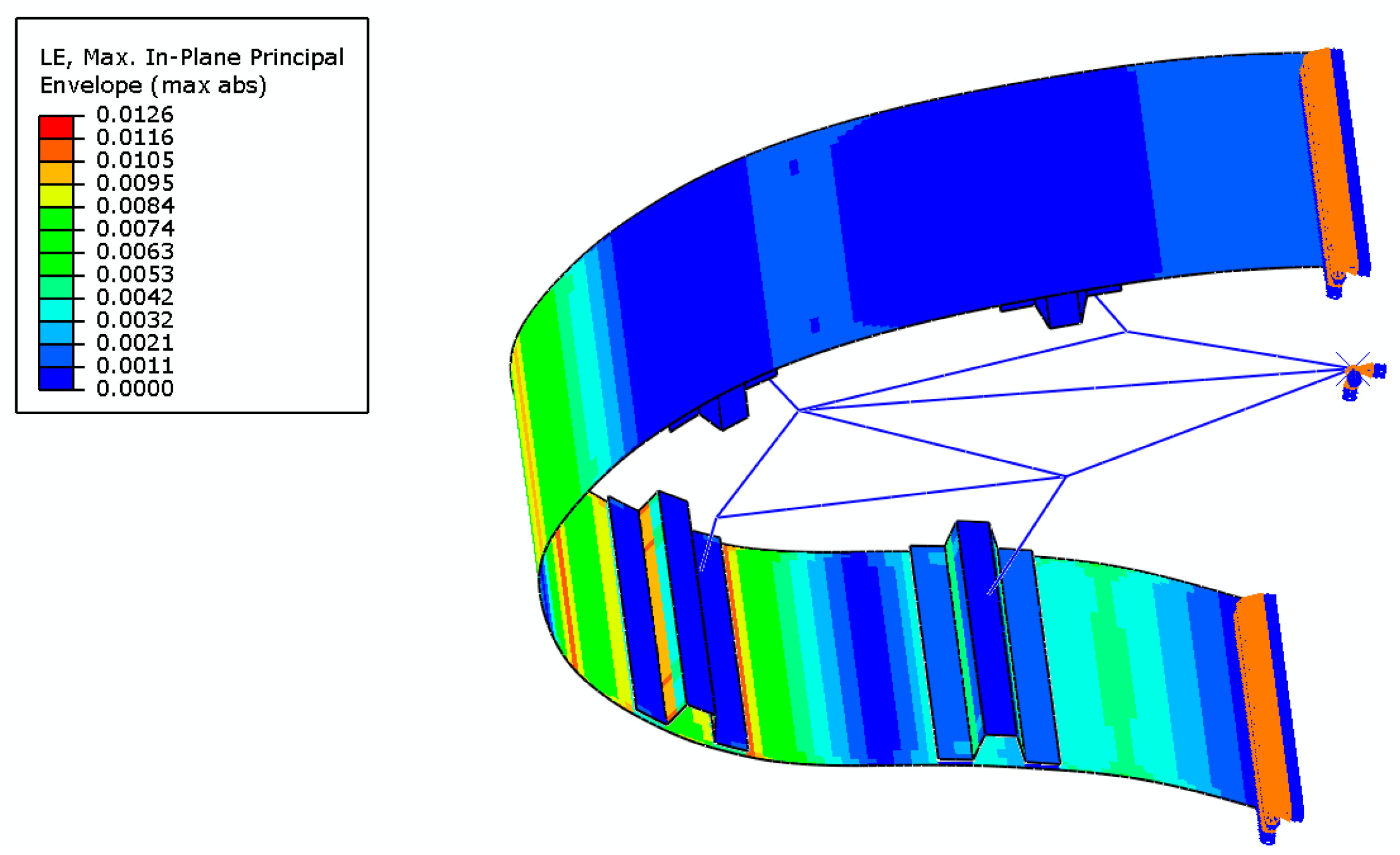
3. Design Approach of Variable-Thickness Compliant Skin
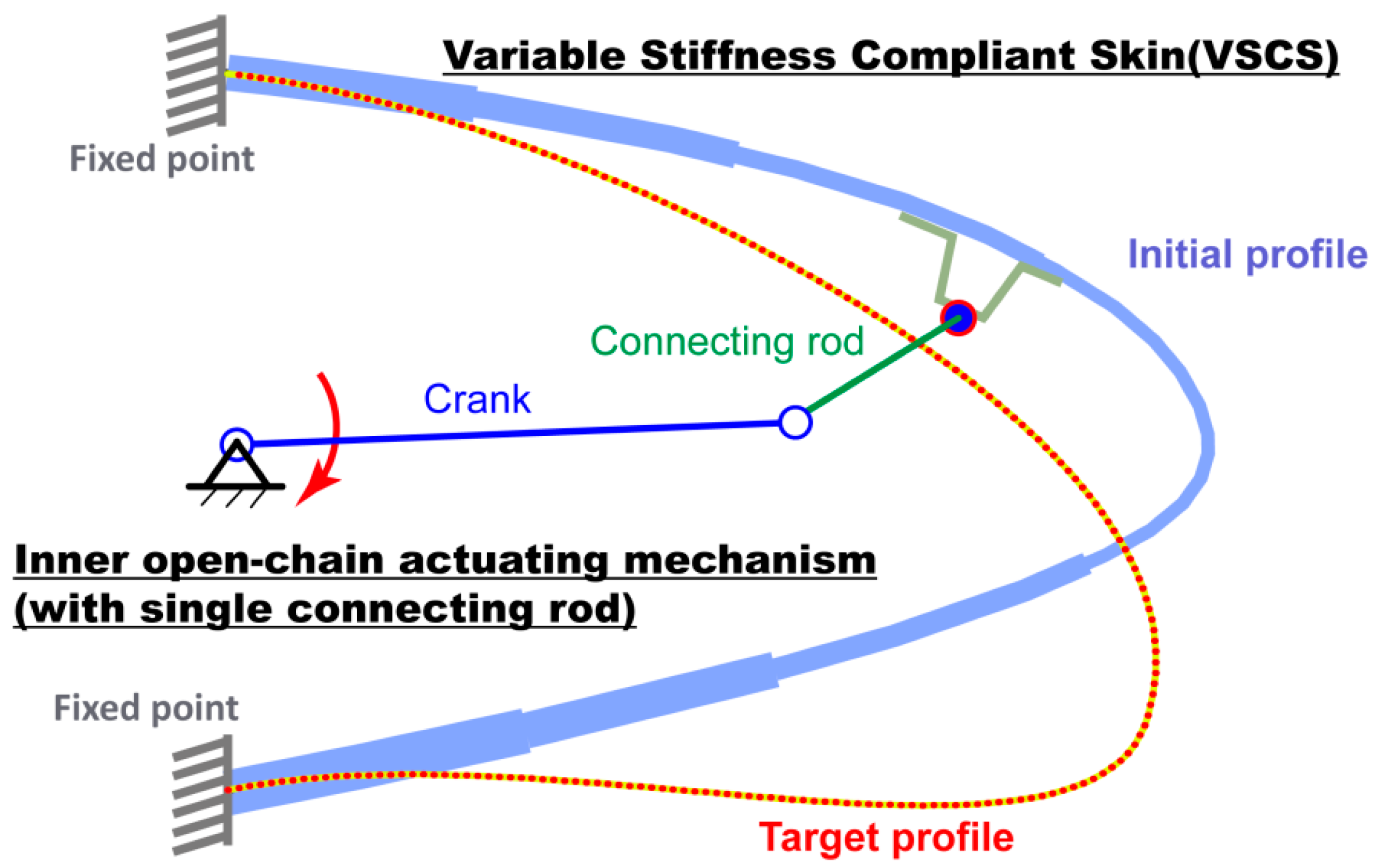
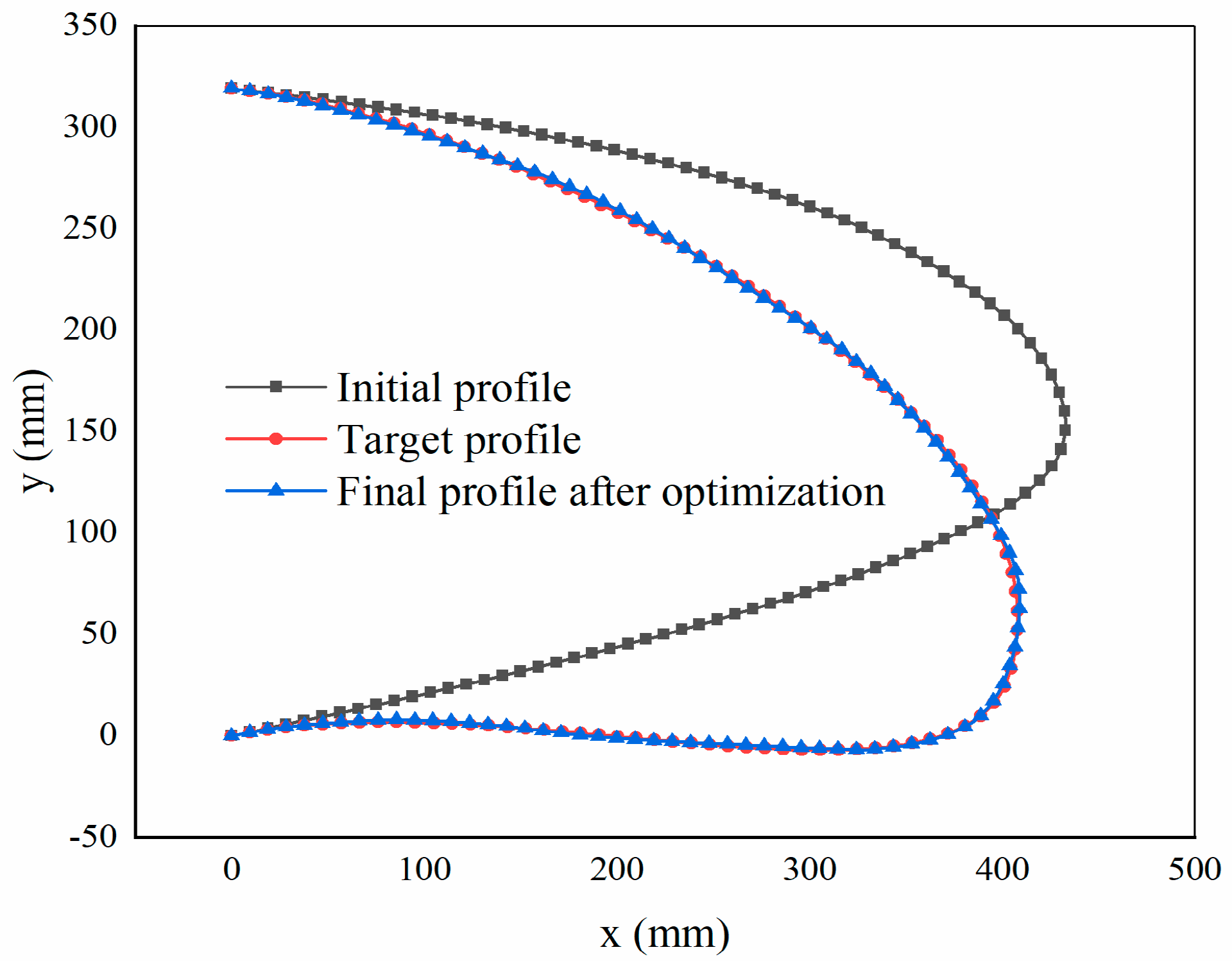
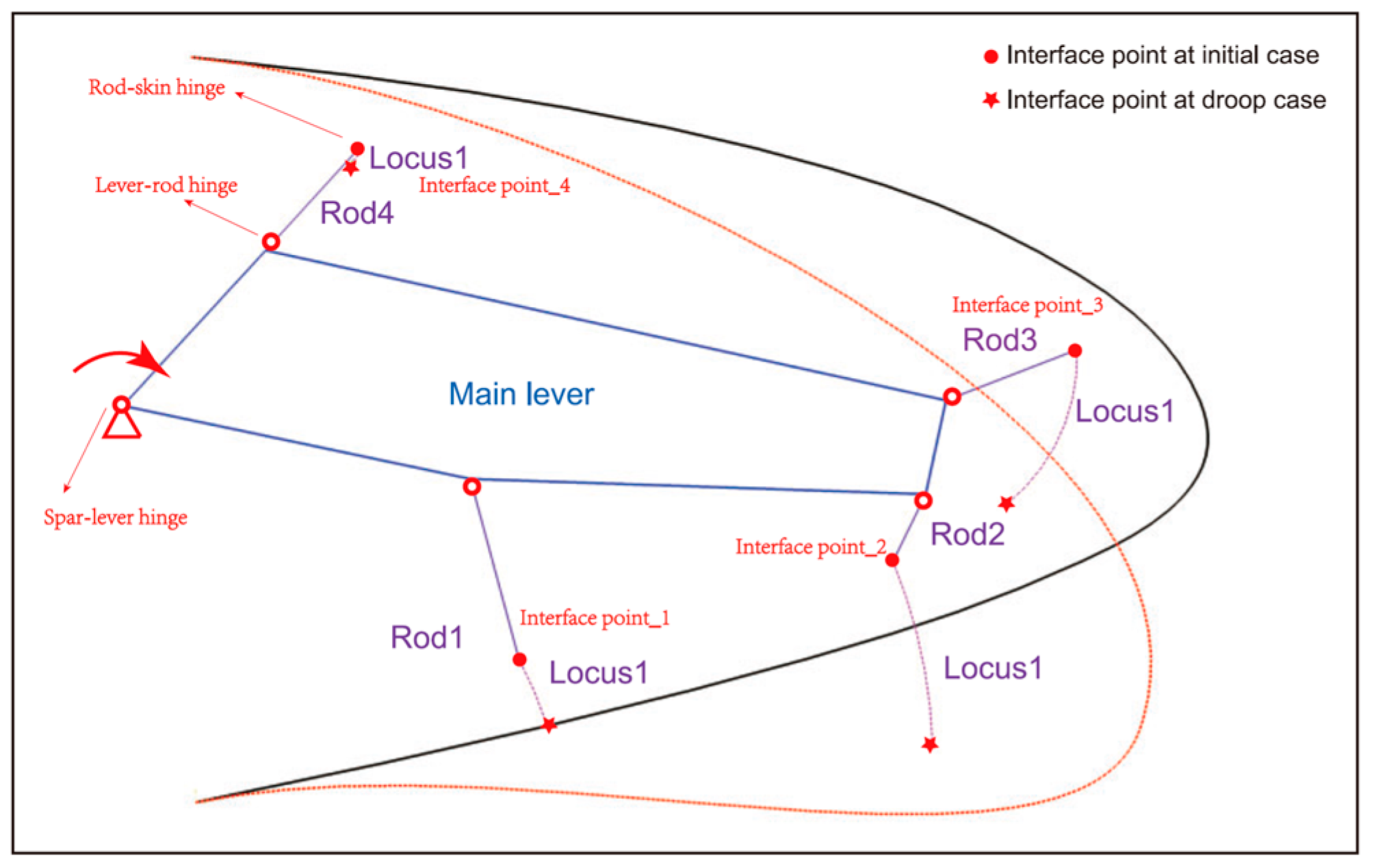
4. Design Approach of Inner Open-Chain Kinematic Mechanism
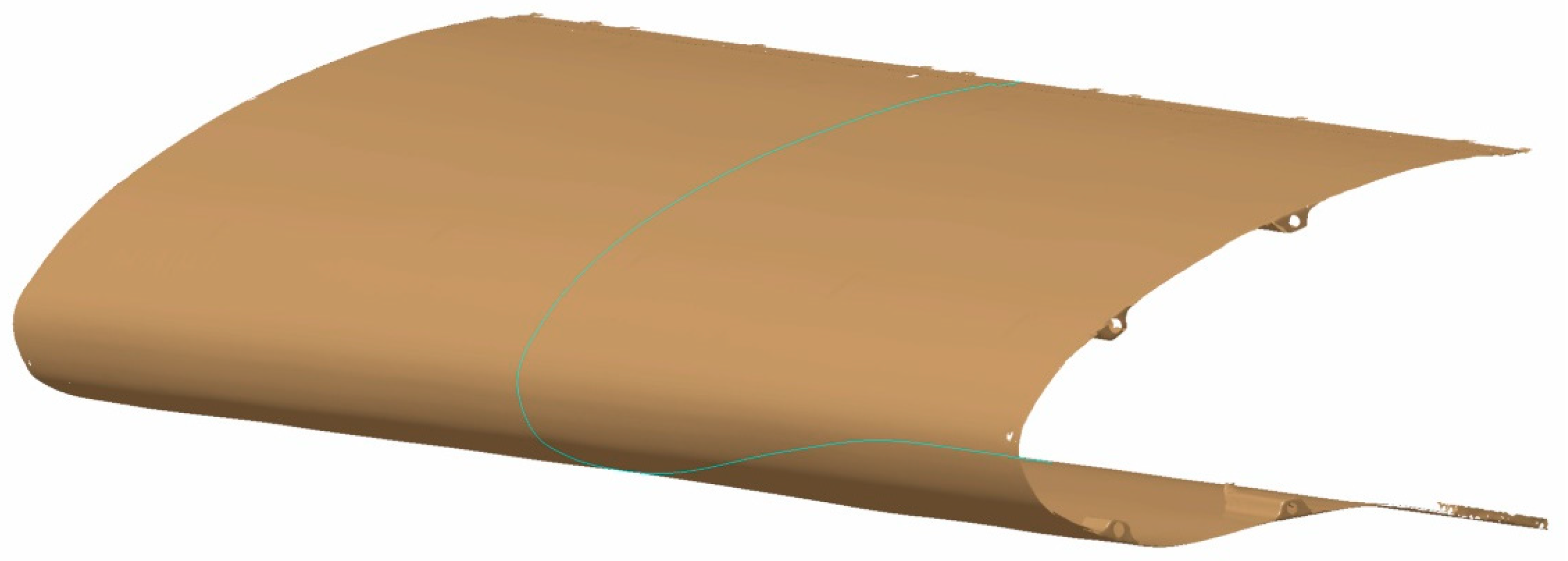
5. Manufacturing and Testing of Morphing Leading Edge
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.W.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; Blanco, G.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar]
- ICAO Environmental Report 2022. Available online: https://www.icao.int/environmental-protection/Documents/EnvironmentalReports/2022/ICAO%20ENV%20Report%202022%20F4.pdf (accessed on 1 November 2022).
- Reckzeh, D. Multifunctional Wing Moveables: Design of the A350XWB and the Way to Future Concepts. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences (ICAS 2014), St. Petersburg, Russia, 7–12 September 2014; International Council of The Aeronautical Sciences (ICAS): St. Petersburg, Russia, 2014; Volume 1, pp. 69–78. [Google Scholar]
- Curiale, N.J.; Zingg, D.W. Morphing Wings: A Study Using Aerodynamic Shape Optimization. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Herr, M.; Pott-Pollenske, M.; Ewert, R.; Boenke, D.; Siebert, J.; Delfs, J.; Rudenko, A.; Büscher, A.; Friedel, H.; Mariotti, I. Large-Scale Studies on Slat Noise Reduction. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; American Institute of Aeronautics and Astronautics: Dallas, TX, USA, 2015. [Google Scholar]
- Lammering, T.; Risse, K.; Franz, K.; Peter, F.; Stumpf, E. Assessment of an Innovative Morphing Leading Edge Considering Uncertainties in Conceptual Design. In Proceedings of the 12th AIAA Aviation Technology, Integration and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012. [Google Scholar]
- Kintscher, M.; Wiedemann, M.; Monner, H.P.; Heintze, O.; Kühn, T. Design of a Smart Leading Edge Device for Low Speed Wind Tunnel Tests in the European Project SADE. Int. J. Struct. Integr. 2011, 2, 383–405. [Google Scholar] [CrossRef]
- Radespiel, R.; Heinze, W. SFB 880: Fundamentals of High Lift for Future Commercial Aircraft. CEAS Aeronaut. J. 2014, 5, 239–251. [Google Scholar] [CrossRef]
- Rudenko, A.; Hannig, A.; Monner, H.P.; Horst, P. Extremely Deformable Morphing Leading Edge: Optimization, Design and Structural Testing. J. Intell. Mater. Syst. Struct. 2018, 29, 764–773. [Google Scholar] [CrossRef]
- Monner, H.P.; Kintscher, M.; Lorkowski, T.; Storm, S. Design of a Smart Droop Nose as Leading Edge High Lift System for Transportation Aircrafts. In Proceedings of the Collection of Technical Papers—AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- Zhong, M.; Hua, J.; Wang, H.; Bai, J. Design and Verification of High-Lift Configuration of Civil Aircraft Standard Model CAE-AVM-HL. Acta Aerodyn. Sin. 2022, 40, 158. [Google Scholar]
- Hua, J.; Zhong, M.; Zheng, S.; Wang, G.; Wang, H.; Bai, J. Design and Database Applications of CAE-AVM Model Cruise Configuration. Acta Aerodyn. Sin. 2022, 40, 133. [Google Scholar]



| E1 (GPa) | E2 (GPa) | Nu12 | G12 (GPa) | εt (μ) | εc (μ) |
|---|---|---|---|---|---|
| 23.3 | 23.2 | 0.1153 | 2.97 | 33,166 | 13,538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sun, X.; Yang, Y.; Liu, G.; Li, D.; Xiang, J. Design Optimization and Testing of Seamless Morphing Leading Edge for Large Civil Aircraft. Eng. Proc. 2024, 80, 49. https://doi.org/10.3390/engproc2024080049
Wang Z, Sun X, Yang Y, Liu G, Li D, Xiang J. Design Optimization and Testing of Seamless Morphing Leading Edge for Large Civil Aircraft. Engineering Proceedings. 2024; 80(1):49. https://doi.org/10.3390/engproc2024080049
Chicago/Turabian StyleWang, Zhigang, Xiasheng Sun, Yu Yang, Gang Liu, Daochun Li, and Jinwu Xiang. 2024. "Design Optimization and Testing of Seamless Morphing Leading Edge for Large Civil Aircraft" Engineering Proceedings 80, no. 1: 49. https://doi.org/10.3390/engproc2024080049
APA StyleWang, Z., Sun, X., Yang, Y., Liu, G., Li, D., & Xiang, J. (2024). Design Optimization and Testing of Seamless Morphing Leading Edge for Large Civil Aircraft. Engineering Proceedings, 80(1), 49. https://doi.org/10.3390/engproc2024080049








