Abstract
With the wide application of UAVs in various industries, solving the complex multi-UAV multi-target problem becomes crucial. The assignment and task planning of multi-UAV and multi-target usually need to consider two scenarios. First, before the UAV executes the task, the number and location of the target points need to be determined. It is equivalent to matching UAVs in a situation where the need is determined. Second, in the process of UAV flight, it is necessary to take into account the existing range of the UAV, the number and position of the changed mission points and carry out real-time UAV mission planning. This paper presents a multi-UAV multi-target collaborative task planning algorithm that takes into account these two scenarios. An integer programming algorithm is used to assign target points, and the constraint condition is the shortest range of UAV. The ant colony algorithm is used to plan the path of a single UAV. In this paper, the UAV delivery of disaster relief materials is taken as an example to carry out mathematical modeling and calculate the algorithm. The simulation process starts from the initial location of the UAV at the airport. After a period of flight, the UAV’s voyage information and target location information are updated to carry out real-time mission planning for the UAV. The maximum range of a single UAV is set at 30,000. The simulation results show that the total path length of four UAVs in pre-mission planning is 70,006.49, and the longest path of a single UAVs is 20645.15. In real-time mission planning, the total path length of four UAVs is 43,633.44, and the longest path of a single UAVs is 14,413.56. Over the course of the entire mission, the total path length of the four UAVs is 54,504.00, and the longest path of a single UAV is 16,434.74. The simulation results show that the solution method designed in this paper is efficient and can realize the real-time path dynamic planning of multi-UAV.
1. Introduction
With the rapid development of UAV technology, its application in military, logistics, agriculture, environmental monitoring and other fields is more and more extensive. However, due to the complexity of UAV mission planning, how to optimize multi-UAV real-time path planning becomes an urgent problem to be solved [1,2,3,4,5]. Real-time path planning is to dynamically plan the path of the UAV according to the real-time changing environment information, the location information of the UAV and the changing target information during the UAV flight to ensure the smooth completion of the UAV mission. However, due to the number of UAVs, the type of tasks, the dynamic change of the environment and other factors, the complexity of a multi-UAV real-time path planning problem increases significantly [6,7,8,9]. The aim of this study is to design an efficient solution to the problem of multi-UAV real-time path planning. Firstly, the characteristics of the UAV real-time path planning problem are analyzed, and a suitable optimization model is established. Then, an efficient solution method is designed to realize the dynamic planning of UAV real-time path. Finally, the effectiveness and superiority of the proposed method are verified by simulation experiments [10,11,12,13,14]. The significance of this study is that by designing an efficient real-time path planning algorithm, it provides an effective solution to the real-time path planning problem of multi-UAV, so as to improve the execution efficiency of UAVs’ missions, reduce the cost of mission execution and provide theoretical support and technical guarantee for the further application of UAVS technology. At the same time, this study will also provide new ideas and methods for the application of the real-time path planning algorithm in complex optimization problems [14,15]. This study will adopt the methods of theoretical analysis, modeling simulation and experimental verification, and design an efficient real-time path planning algorithm through the in-depth study of the UAV real-time path planning problem in order to provide useful references for the research and application in related fields.
2. Mathematical Algorithm Description
2.1. Integer Programming Is Applied to Multi-UAV Target Allocation
Integer programming requires that all the solutions are integers, and finally makes the objective function obtain the maximum or minimum value. However, for UAVS mission planning, all the optimal solution variables are required to be integers, and the desired objective function value is minimum. The problem of multi-UAV task assignment can be solved by using integer programming. Moreover, the optimal solution obtained by integer programming is stable, and the solution speed is faster when the target point is less than 100. Because integer programming has two characteristics of stable results and fast solving speed, this paper selects integer programming for task assignment of multi-UAV. The standard model for integer programming is as follows:
According to the requirements of the variables in this paper, the 0–1 integer programming is selected. The value of a variable can only be 0 or 1, also known as a 0–1 variable or binary variable. The 0–1 variable is a logical variable used to indicate whether the system is in a certain state, and its mathematical model is
min z = CX
In Formula (3), z represents the total path of the UAV, X is the calculated coefficient, 0 means that the UAV in the calculation did not choose the target point to perform the task and 1 means that the UAV in the calculation chose the target point to perform the task. The objective function is to make the total path of all UAVs the shortest. (4) Type A is the distance between the target and the UAV, and between the target and the target. X is the initial given coefficient, 0 means that the UAV in the calculation did not choose the target point to perform the task and 1 means that the UAV in the calculation process chose the target point to perform the task. b is the maximum range that each UAV can fly.
The basic idea of solving 0–1 integer programming: When there are n decision variables in the model, different combinations of variables may be generated, and only a part of these combinations often meets all constraints. This decomposition is called the basic feasible solution. The objective function value of the basic feasible solution is obtained, and the best one is selected by comparing all the objective function values, which is called the optimal value.
2.2. Application of Ant Colony Algorithm and Single UAV Path Planning
The ant colony algorithm is a probabilistic algorithm, which can be used to search the optimal path in the environment map and solve various optimization problems. Because of the special advantage of the ant colony algorithm in searching for the shortest path, the ant colony algorithm is selected for single UAV path planning after the integer programming is used for sub-task assignment. The mathematical model of the basic ant colony algorithm is described as follows:
The ant colony algorithm is applied to solve the shortest path problem of UAVs and the corresponding relationship between the UAVs’ path planning data. The initial input value of ant colony algorithm is set to the number of ants, the number of sites, the distance between sites, the initial pheromone concentration and other parameters. In UAV path planning, the number of ants can be set to an empirical value, the same as the ant colony algorithm applied to other algorithms. The number of locations is the sum of the number of target points corresponding to the UAV. The distance between locations is the distance between the UAV and the target point and the distance between the target point and the target point. The initial pheromone concentration is an empirical value, consistent with the ant population, and can be given a value with reference to other applications. In the process of solving the shortest path, path construction includes the selection of the initial target point and the selection of the next target point. Each ant randomly selects a target point as its starting point and maintains a memory table to store the target points passed by the ant (this is the difference between artificial ants and natural ants). At each step of the path construction, ants choose the next target point to reach according to the ant cycle model. At time t, the transfer probability of ant k from target point i to target point j is calculated as follows:
In the formula, is the walkable area of ant k at position point i, the position that the ant has not walked, that is, the set of all position points connected with position i that ant k can visit at t + 1. α is an information heuristic factor, indicating the influence of pheromone on path selection probability. The larger α is, the more ants tend to choose the path taken by most ants, and the stronger the interference ability of pheromone on ants is. Beta is the expectation heuristic factor, and the larger the beta, the more the ants are influenced by the distance between way points and the more you tend to select the grid closer to the target point. represents the pheromone concentration between time t region i and j; is a heuristic function that represents the expectation between time t region i and j.
where () is the coordinate of the ant’s current position, and () is the position coordinate of the next node to be selected. represents the distance from the position point i to the next point j. The smaller is, the larger is, and the greater the state transition probability (t) is. Where is the distance between the UAV and the target, and between the target and the target, because the calculated distance is the shortest, so the pheromone here is represented by the distance.
According to the context analysis, the pheromone itself has the nature of self-renewal, so that the interference of concentration difference on each path can be reduced to ensure the normal operation of the algorithm. Let ρ represent the amount of pheromone volatilization by ants searching for a certain path. After n moments, the whole colony will complete a cyclic feeding movement, at which time the pheromone concentration on each path will be adjusted according to the following formula:
Formula (8) represents the global pheromone concentration update rule, where ρ is the coefficient of pheromone concentration play, (1 − ρ) is the coefficient of pheromone concentration residual on the path and the value range of ρ is set as ρ∈ (0,1). Formula (9) indicates that the pheromone increments on the path (i,j) are determined by the sum of the pheromone increments released by the ants in the entire colony. Where means that the kTH ant is looking for the amount of pheromone released on the path in one cycle. The process of M ants moving once in the practice range (t, t + 1) is called an iterative process of the ant colony algorithm. After n iterations, the ant colony algorithm completes a cycle. In the process of solving pheromone increment, the ant cycle model is used, and the model formula is (10).
Q is the pheromone intensity coefficient and is the path length traveled by ant K.
3. Data Analysis
3.1. Experimental Hypothesis and Data Description
(1) The UAV departs from an airport;
(2) There is no limit on the number of mission points, but a UAV has a range limit, and each flight is 30,000;
(3) Only one UAV is allowed to perform missions at each mission point;
(4) Assume that each UAV is flying at a fixed cruising altitude, so there is no conflict between the UAVs;
(5) The priority of all objectives is the same, that is, there is no difference in the order of implementation;
The UAVs start at the airport, the coordinate of the airport is (4562.32,5468.45), and there are 28 target points obtained before takeoff. The number and location information of target points are shown in the following Table 1:

Table 1.
Location information of the initial 28 no target points.
3.2. Location Distribution Map of Airports and Target Points
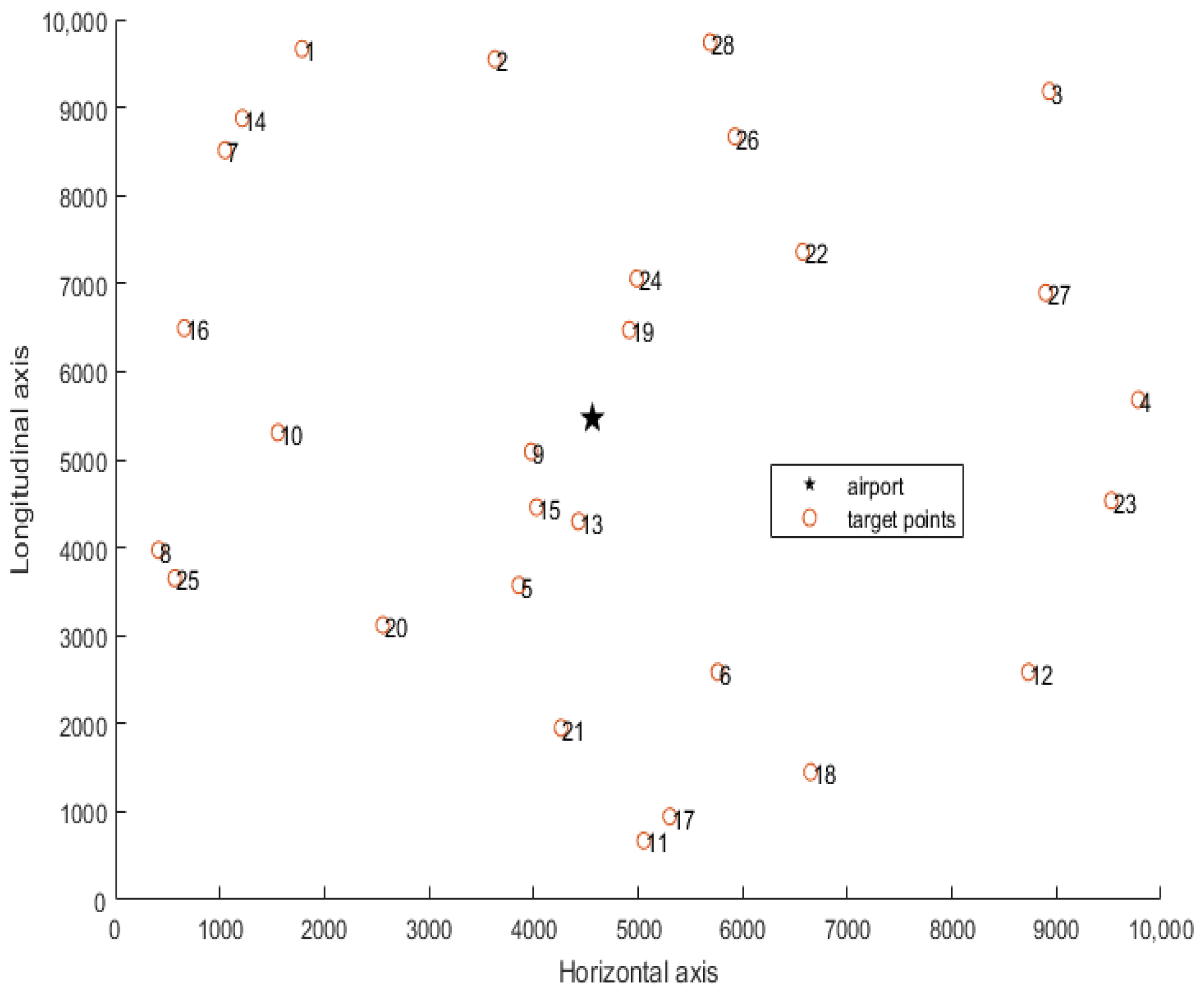
In order to more intuitively display the coordinate spatial distribution position of the airport and the target points, draw the location information of the airport and the target points in a two-dimensional rectangular coordinate system. The black star is the coordinate position of the airport, and the hollow circles are the center coordinate position of each targets. The distribution diagram is as follows (Figure 1):
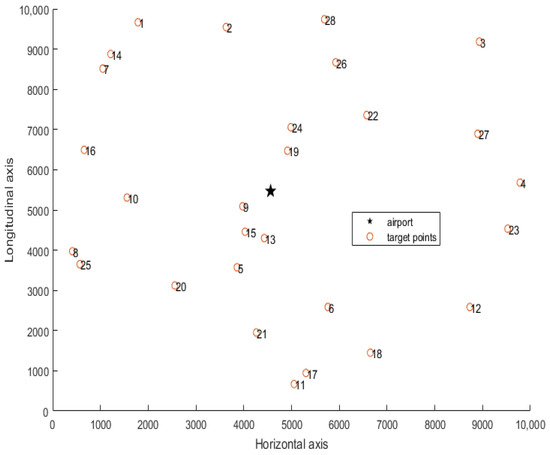
Figure 1.
Location distribution of airports and target points.
3.3. Pre-Task Planning of the Airport
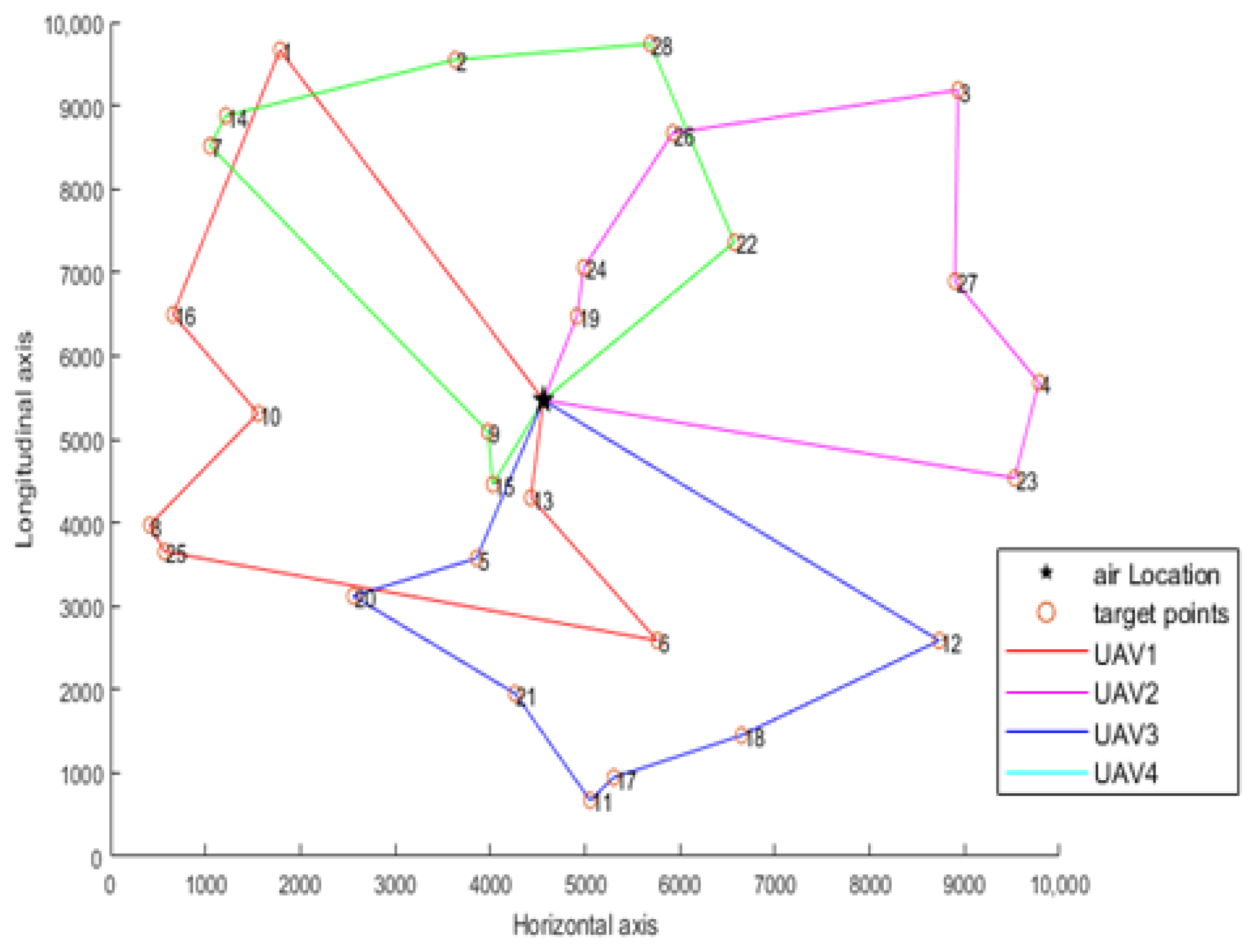
The integer programming algorithm is used to assign tasks to the target points, and then the ant colony algorithm is used to plan the tasks assigned by each UAV, and the path planning results of each UAV are obtained. After calculation, the path planning results of the first UAV are 1, 16, 10, 8, 25, 6 and 13, and the path length is 20,645.15. The path planning results of the second UAV are 22, 28, 2, 14, 7, 9 and 15, and the path length is 16,553.72. The path planning results of the third UAV are 5, 20, 21, 11, 17, 18 and 12, and the path length is 16,222.18. The path planning results of the fourth UAV are 19, 24, 26, 3, 27, 4 and 23, and the path length is 16,585.44. The four UAVs departed from the airport, and the total path length of the four UAVs is 70,006.49. The route planning diagram of airport pre-task planning is shown in Figure 2.
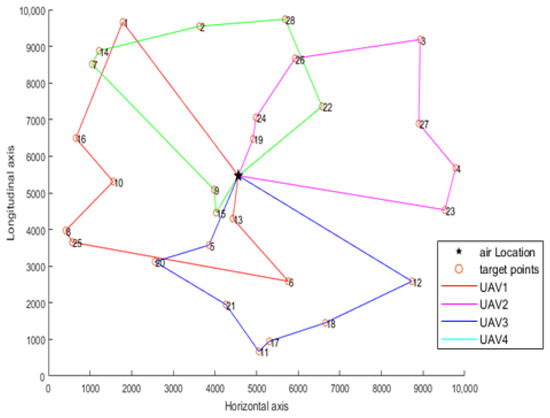
Figure 2.
Path planning diagram of prior task planning.
3.4. Real-Time Planning During Flight
After taking off for some time, it is assumed that the UAVs have flown to the first mission point of the pre-planned mission route. Calculate the distance of each of the four UAVs traveled from the airport to the time they received the mission, which in real flight would be read from the UAVs’ telemetry data. The first UAV flew a distance of 5032.71 and the remaining distance is 24,967.29; the second UAV flew a distance of 2021.18 and the remaining distance is 27,239.63; the third UAV flew a distance of 1065.33, with 27,978.82 remaining; the fourth UAV flew a distance of 2760.37 and the remaining distance is 28,934.67. The current numbers and locations of the four UAVs are shown in Table 2.

Table 2.
Current position information of UAVs.
The data that need to be adjusted for real-time mission planning include the current position of the UAVs and the adjusted target point (adding the newly added target point and deleting the target point that is no longer of concern). Two new target points were added in this experiment. The coordinates of the new target points were as follows: (5605.34, 6098.94) and (9382.69, 1892.32), and the new target points were labeled 29 and 30. The number and location information of the target points are shown in the following Table 3: 1, 5, 19 and 22 points have been removed from the original target points, which are the locations of the current UAVs.

Table 3.
Location information of target points in real-time task planning.
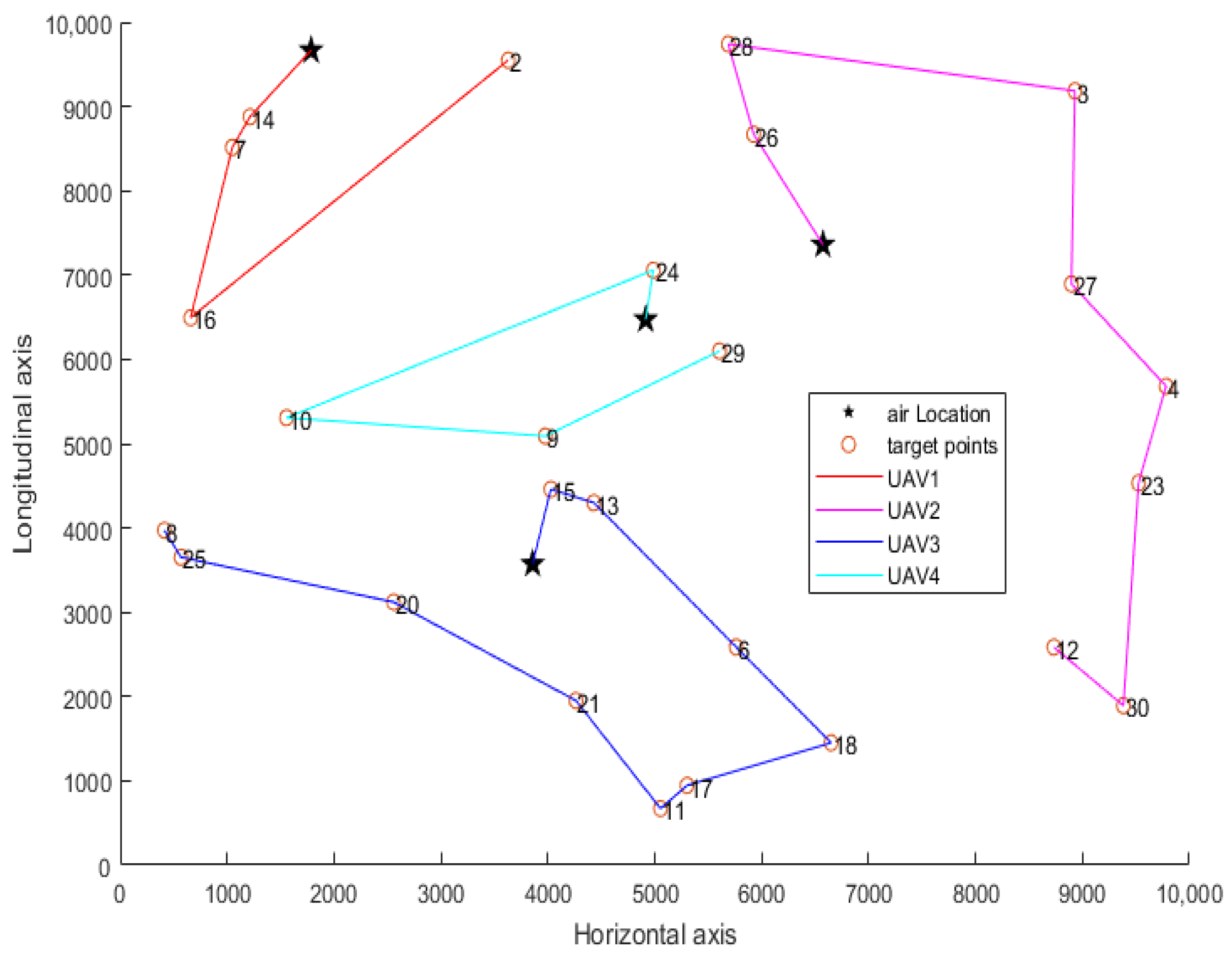
Integer programming is used to assign UAVs and targets, and the ant colony algorithm is used to plan the path of single UAV. The assignment results of the four UAVs are as follows (Figure 3): the real-time task planning results of the first UAV are 12, 5, 14 and 1, and the path length is 7690.89; the real-time mission planning results of the second UAV are 26, 28, 3, 27, 4, 23, 30 and 12, and the path length is 14,413.56; the real-time mission planning result of the third UAV is 15, 13, 6, 18, 17, 11, 21, 20, 25 and 8, and the path length is 12,741.42; the path planning results of the fourth UAV are 24, 10, 9 and 29, and the path length is 8787.54. The total path length planned for this UAV mission is 43,633.44.
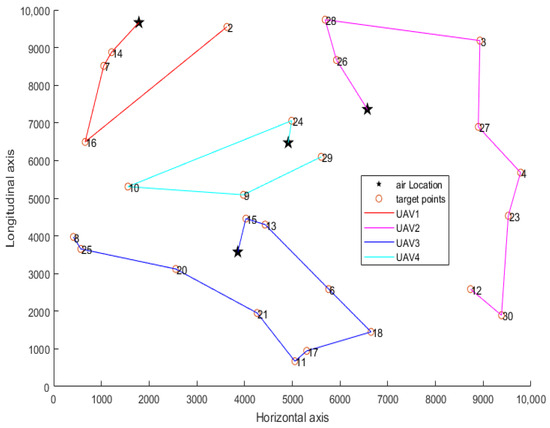
Figure 3.
Path planning diagram of real-time task planning.
3.5. Task Planning Method Combining Random Assignment and Ant Colony Algorithm
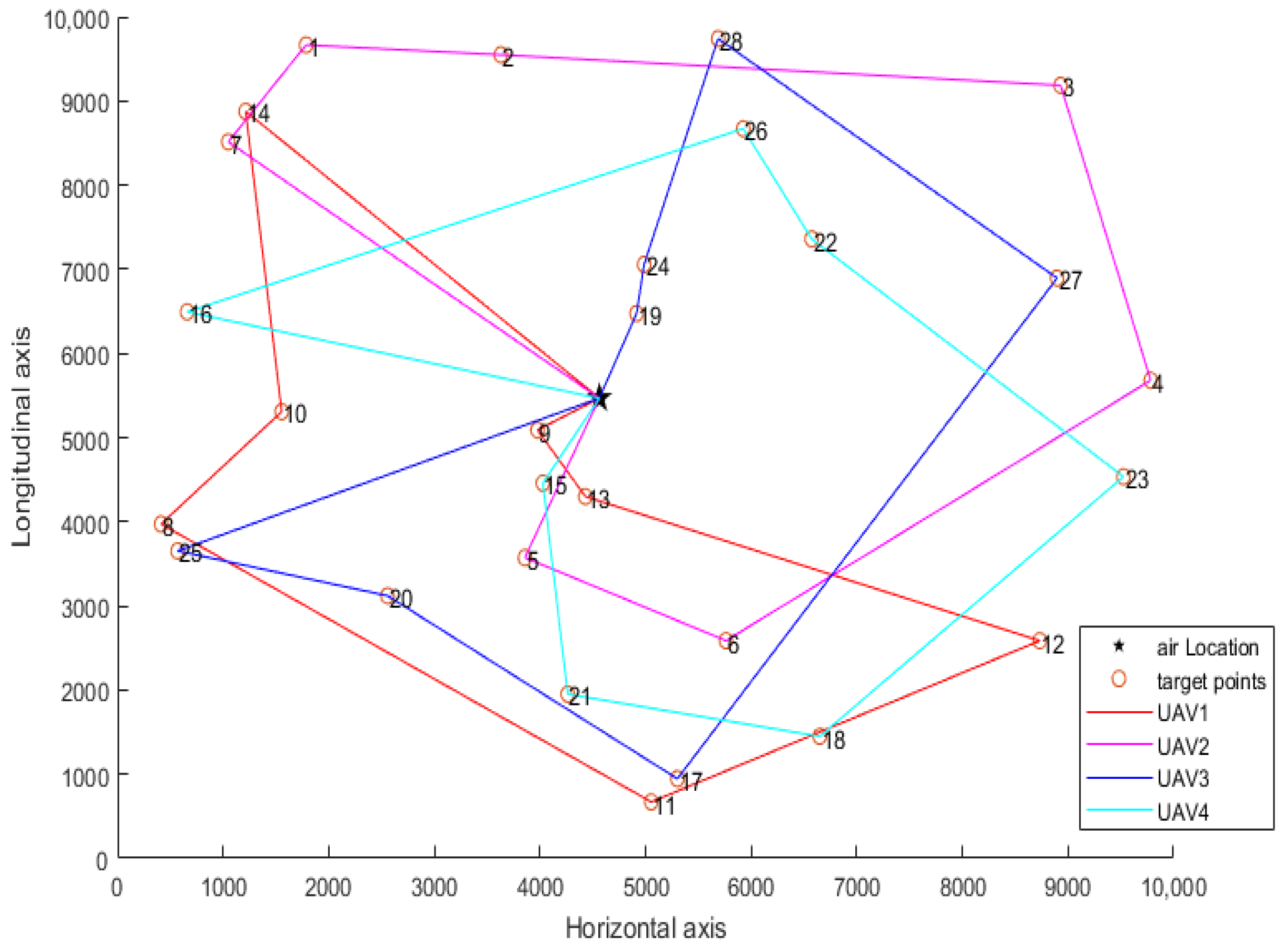
Randomly and evenly divide the target points into an equal number of UAVs. Then, the ant colony algorithm is used to plan the assigned tasks and the path planning results of each UAV are obtained. Randomly assign 10 target points, and then select the group with the shortest total path to compare with the proposed algorithm. The path planning results of the first UAV are 9, 13, 12, 11, 8, 10, 14, and the path length is 26,203.42. The path planning results of the second UAV are 5, 6, 4, 3, 2, 1 and 7, and the path length is 26,023.69. The path planning results of the third UAV are 19, 24, 28, 27, 17, 20 and 25, and the path length is 25,612.42. The path planning results of the fourth UAV are 15, 21, 18, 23, 22, 26 and 16, and the path length is 21,561.56. The four UAVs departed from the airport, and the total path length of the four UAVs is 99,401.09. The route planning diagram of airport pre-task planning with randomly assigned target points is shown in Figure 4.
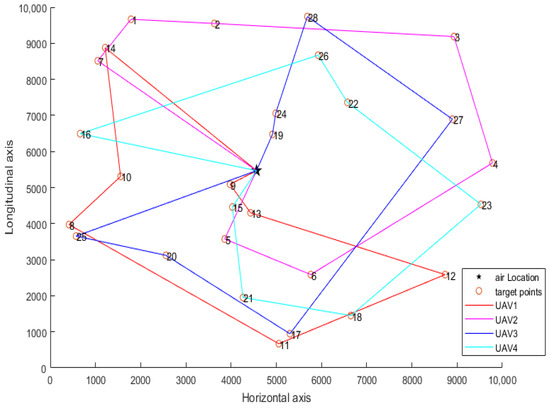
Figure 4.
Path planning diagram of randomly assigned target points.
4. Result Analysis
The planning of UAVs in the airport is a scheduling and allocation planning problem with sufficient resources, and the planning of UAVs in the air is a task planning problem with limited resources. In this paper, the integer programming algorithm is used to assign tasks between UAVs and target points, and then the ant colony algorithm is used to plan tasks for single UAVs. In pre-task planning, 28 task points were assigned to four UAVs. The total path length of the four UAVs is 70,006.49, and the longest path of a single UAV is 20,645.15. In the course of this task assignment, the total range of the first UAV is 12,723.60; the second UAV has a total range of 16,434.74; the third UAV has a total range of 13,797.75; the fourth UAV has a total range of 11,547.91. Finally, the algorithm proposed in this paper is verified by a random allocation method, and the total path planned by the allocation algorithm before work is 99401.09. The simulation results show that the integer programming presented in the paper can do multi-UAV task assignment, and the ant colony algorithm can plan the path of single UAVs. The algorithm can achieve good results and can calculate the short route that meets the needs of use. The proposed algorithm is practical and effective.
Author Contributions
In this paper, W.H. provided the conceptualization and the overall design ideas for the cluster path planning, including the task allocation and task planning algorithms. J.B. was responsible for the algorithm implementation, programming, data construction, and the design of the comparative testing method. M.C. was in charge of writing the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received the company’s internal research project funding. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication, Project number: K2402.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Jingzhi Bi was employed by the company CH UAV Science & Technology Co., Wei Huang was employed by the company CH UAV Science & Technology Co., Maihui Cui was employed by the company CH UAV Science & Technology Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lv, Z.; Gao, K. Review of the development of UAV swarm urban combat applications in the USA. J. China Acad. Electron. Inf. Technol. 2020, 15, 738–745. [Google Scholar]
- Maoh, B.; Tian, S.; Chao, A.N. Unmanned Aerial Vehicle Mission Planning. Master’s Thesis, National Defense Industry Press, Beijing, China, 2015; pp. 76–80. (In Chinese). [Google Scholar]
- Ren, X.; Tan, L.; Jiaqi, S.; Lian, X. Multi-target UAV path planning based on improved RRT algorithm. J. Phys. Conf. Ser. 2012, 1786, 012038. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, F.; Fang, X.; Lan, Z. Improved bat algorithm for UAV path planning in three-dimensional Space. IEEE Access 2021, 9, 20100–20116. [Google Scholar] [CrossRef]
- Jayaweera, H.M.; Hanoun, S. A Dynamic Artificial potential Field (D-APF) UAV Path Planning Technique for Following Ground Moving Targets. IEEE Access 2020, 8, 192760–192776. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Y.; Mu, L.; Huang, J.; Xin, J.; Liu, H.; Jiao, S.; Xie, G.; Yi, Y. A UAV Path Planning Algorithm Based on an Improved D Lite Algorithm for Forest Firefighting. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4233–4237. [Google Scholar]
- Xue, Y.; Sun, J.Q. Solving the path planning problem in mobile robotics with the multi-objective evolutionary algorithm. Appl. Sci. 2018, 8, 1425. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Song, Y.; Zhao, H. An effective improved co-evolution ant colony optimization algorithm with multi-strategies and its application. Int. J. Bio-Inspired Comput. 2020, 16, 158–170. [Google Scholar] [CrossRef]
- Dasdemir, E.; Koksalan, M.; Ozturk, D.T. Aflexible reference point-based multi-objective evolutionary algorithm: An application to the UAV route planning problem. Comput. Oper. Res. 2020, 114, 104811. [Google Scholar] [CrossRef]
- Radmanesh, M.; Kumar, M.; Sarim, M. Grey wolf optimization based sense and avoid algorithm in a Bayesian framework for multiple UAV path planning in an uncertain environment. Aerosp. Sci. Technol. 2018, 77. [Google Scholar] [CrossRef]
- D’Urso, F.; Santoro, C.; Santoro, F.F. An integrated framework for the realistic simulation of multi-UAV applications. Comput. Electr. Eng. 2019, 74, 196–209. [Google Scholar] [CrossRef]
- Ning, Q.; Tao, G.P.; Chen, B.C.; Lei, Y.; Yan, H.; Zhao, C. Multi-UAVs trajectory and mission cooperative planning based on the Markov model. Phys. Commun. 2019, 35, 1007–1017. [Google Scholar] [CrossRef]
- Yang, J.; You, X.H.; Wu, G.X.; Hassan, M.M.; Almogren, A.; Guna, J. Application of reinforcement learning in UAV cluster task scheduling. Future Gener. Comput. Syst. 2019, 95, 140–148. [Google Scholar] [CrossRef]
- Liu, C.; Xie, W.-J.; Zhang, P.; Guo, Q. Collaborative Mission Planning of Multi-Target Group Multi-Base and Multi-UAV. J. Proj. Rockiets J. Ammunit. Guid. 2019, 39, 119–124. [Google Scholar]
- Wang, R.-R.; Wei, W.-L.; Yang, M.-C.; Liu, W. Task Allocation of Multiple UAVs Considering Cooperative Route Planning. J. Aeronaut. 2020, 41, 24–35. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).