Design of Gain-Scheduled Lateral Controllers for Autonomous Vehicles ^†

Abstract

This paper focuses on the design and comparative analysis of speed-dependent lateral control systems for autonomous vehicles, focusing on optimizing vehicular dynamics and passenger comfort to ensure stability and safety. Adapting control systems to varying speeds becomes crucial for maintaining stability and maneuverability as autonomous technologies progress. This study evaluates their effectiveness in real-time navigation scenarios within a simulated environment by applying gain-scheduled linear quadratic regulators and model predictive control. The results show that while traditional controllers, such as Pure Pursuit, perform adequately under constant speed conditions, adaptive model-based algorithms significantly enhance the performance, especially in dynamic driving situations involving speed variations.

1. Introduction

The study of vehicle lateral control has been ongoing since the 1950s, driven by evolving technological demands and challenges, particularly in the development of autonomous vehicles. These vehicles aim to imitate human driving behavior, improve safety, reduce human errors, and increase the transportation efficiency. Traditional control systems, such as Pure Pursuit and Stanley controllers, have been widely used in various applications [1,2]. However, their performance decreases when handling more complex and dynamic driving tasks, leading to the development of model-based solutions. Initially based on linear dynamics, these solutions have progressively incorporated more advanced, nonlinear model-based strategies to manage the variability in system parameters [3].

Over the years, the integration of passenger comfort into the design of lateral controllers has gained attention. Providing a more human-like driving experience increases the thrust in these systems, which positively affects the marketability of the system. Therefore, more complex control algorithms are needed to handle the tightening requirements. Recent studies on model-based control development utilize nonlinear model predictive control (nMPC) algorithms. These algorithms use nonlinear predictive models to precisely describe the vehicle dynamics and optimize the control actions based on future states [4]. Furthermore, nMPC methods can also handle nonlinear constraints and time-varying dynamics, thus significantly enhancing the responsiveness and adaptability of autonomous driving systems.

Besides the tracking accuracy and computational capacity, other aspects, such as robust stability, have shaped the design of lateral controllers [5,6]. The application of Lyapunov functions in the stability analysis of dynamic systems has provided a robust mathematical background to guarantee the stability of control systems under various conditions. These methods ensure that the closed-loop system remains stable even in the presence of perturbations and converges back to a desired state without excessive oscillations or deviations [7].

A different approach is to utilize machine learning algorithms to control autonomous vehicles. For instance, Ref. [8] presents a double Q-learning-based approach to mimic human driving behavior accurately. On the other hand, Ref. [9] presents a deep reinforcement learning-based car-following model, which outperforms traditional and data-driven car-following models while also demonstrating good generalization capabilities.

In some cases, model-based algorithms are combined with machine learning to combine the advantages of both techniques. Such an example is presented in [10], where the parameters of a traditional PID controller are optimized using genetic algorithms for better performance [10].

While implementing speed-dependent controllers is crucial to mitigate the effects of varying driving conditions, the computational capacity of the algorithms must also be considered. Techniques such as gain scheduling and linear parameter varying (LPV) control offer viable solutions to high-complexity, nonlinear algorithms. In lateral vehicle controllers, controller gains are adjusted based on the velocity of the vehicle [11,12]. Despite their low computational cost, gain scheduling techniques enhance performance, comfort, and dynamic stability of the vehicle [13].

Contribution

The main contribution of this paper lies in the development, analysis, and comparison of three speed-dependent lateral control algorithms: a linear quadratic regulator (LQ), a linear quadratic integral controller (LQ-Servo), and a model predictive controller (MPC). These algorithms are tuned in a CarMaker environment, and their performance is compared concerning tracking accuracy and passenger comfort. At the same time, a traditional Pure Pursuit (PP) algorithm is also presented as a benchmark. This paper provides a comprehensive evaluation of these control strategies under the same conditions.

This paper is organized as follows: Section 2 introduces the lateral vehicle model used for controller synthesis. Section 3 details the implemented control strategies. Section 4 presents the simulation environment and the results of the comparative analysis. Finally, Section 5 concludes the paper with remarks on the findings and suggests directions for future research.

2. Lateral Vehicle Model

The lateral dynamics of a vehicle are mainly described using the dynamic bicycle model, which represents the vehicle as a single-track system. This model describes the lateral motion and yaw rotation of the vehicle using the following differential equations:

$$m\left(\ddot{y}+V_x\dot{\psi }\right)=F_{yf}+F_{yr},$$

(1)

$$I_z\ddot{\psi }={\mathcal{l}}_f{F}_{yf}-{\mathcal{l}}_r{F}_{yr},$$

(2)

where m is the vehicle mass, I_z is the yaw moment of inertia, V_x is the longitudinal velocity, $\ddot{y}$ is the lateral acceleration, $\dot{\psi }$ is the yaw rate, F_yf and F_yr are the lateral tire forces, and l_f and l_r are the distances from the center of gravity to the front and rear axles, respectively.

While the traditional model can describe the behavior of the vehicle under various conditions, ref. [14] proposes applying a slightly modified (tracking) model. It represents the lateral deviation and orientation error of the vehicle relative to the desired path. The state-space representation of the tracking model is formulated as follows:

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -{\displaystyle \frac{2C_f+2C_r}{m{V}_x}}& {\displaystyle \frac{2C_f+2C_r}{m{V}_x}}& {\displaystyle \frac{-2C_f{l}_f+2C_r{l}_r}{m{V}_x}}\\ 0& 0& 0& 1\\ 0& -{\displaystyle \frac{2C_f{l}_f-2C_r{l}_r}{I_z{V}_x}}& {\displaystyle \frac{2C_f{l}_f-2C_r{l}_r}{I_z}}& -{\displaystyle \frac{2C_f{l}_f^2+2C_r{l}_r^2}{I_z{V}_x}}\end{array}\right]\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{2C_f}{m}}\\ 0\\ {\displaystyle \frac{2C_f{l}_f}{I_z}}\end{array}\right]\delta +\left[\begin{array}{c}0\\ -{\displaystyle \frac{2C_f{l}_f+2C_r{l}_r}{m{V}_x}}-V_x\\ 0\\ -{\displaystyle \frac{2C_f{l}_f^2+2C_r{l}_r^2}{I_z{V}_x}}\end{array}\right]{\psi }_{des},$$

(3)

where e₁ is the lateral deviation, e₂ is the orientation error, C_f and C_r are the cornering stiffness coefficients of the front and rear tires, δ is the steering angle, and ψ_des is the desired yaw rate.

The model is formulated using a grid-based LPV representation to incorporate the speed-dependent dynamics of the system.

3. Control Synthesis

This section details the theoretical background and implementation of the presented controllers, including the Pure Pursuit, linear quadratic regulator, linear quadratic servo, and model predictive control methods. All of the presented controllers have been implemented in discrete time with a sampling time of 1 ms.

3.1. Pure Pursuit

The Pure Pursuit method is a geometric-based approach used for path tracking problems in autonomous vehicles. The steering angle required to follow a given path is calculated by considering the current position of the vehicle and the look-ahead point on the path. The steering angle δ is determined by the following equation:

$$\delta =\arctan \left({\displaystyle \frac{2L\sin \left(\alpha \right)}{L_d}}\right),$$

(4)

where L is the wheelbase, α is the angle between the heading of the vehicle and the line connecting the rear axle to the lookahead point, and L_d is the lookahead distance, which significantly affects the tracking accuracy of the algorithm.

One of the main drawbacks of Pure Pursuit is that it relies on a kinematic vehicle model. Hence, it cannot handle dynamic driving conditions.

3.2. Linear Quadratic Regulator

The linear quadratic regulator (LQ) is a fundamental algorithm in control theory [15]. The LQ controller is designed to minimize a quadratic cost function that balances state deviations x(k) and the control effort u(k):

$$J=\sum _{k=0}^{\mathrm{\infty }} \left(x\left(k{)}^{T}Qx\right(k)+u(k{)}^{T}Ru\left(k\right)\right),$$

(5)

where Q and R are positive (semi-)definite weighting matrices. The state-space model is discretized, and the above criterion is defined for the discretized state equation. The optimal feedback gain K is computed by solving the Discrete-Time Algebraic Riccati Equation (DARE):

$$A^{T}PA-P-A^{T}PB{\left(B^{T}PB+R\right)}^{-1}{B}^{T}PA+Q=0,$$

(6)

where A is the state transition matrix, B is the input matrix, and P is a positive definite matrix, the solution of the Riccati Equation. The optimal control input u(k) is given as

$$u\left(k\right)=-Kx\left(k\right).$$

(7)

3.3. Linear Quadratic Servo

The LQ-Servo extends the LQ by incorporating an integrator to eliminate steady-state errors, enhancing trajectory-tracking accuracy. The augmented state-space model includes the integral of the output error z(k):

$$\left[\begin{array}{c}x\left(k+1\right)\\ z\left(k+1\right)\end{array}\right]=\left[\begin{array}{cc}A& 0\\ -C& I\end{array}\right]\left[\begin{array}{c}x\left(k\right)\\ z\left(k\right)\end{array}\right]+\left[\begin{array}{c}B\\ 0\end{array}\right]u\left(k\right),$$

(8)

where I is an identity matrix, B is the input, and C is the output matrix. The optimal control input is

$$u\left(k\right)=-Kx\left(k\right)-K_{z}z\left(k\right),$$

(9)

where K is the state feedback, and K_z is the integral action gain matrix.

3.4. Model Predictive Control

Finally, an MPC has been implemented based on [16]. At each time step, it solves a finite horizon optimization problem by considering future states and control actions. The state-space model is reformulated in terms of change in the state vector $\mathsf{\Delta }x$ and the control input $\mathsf{\Delta }u$ to eliminate steady-state error:

$$\mathsf{\Delta }x\left(k+1\right)=A\mathsf{\Delta }x\left(k\right)+B\mathsf{\Delta }u\left(k\right).$$

(10)

Then, the augmented state-space equations are written as follows:

$$\widehat{x}\left(k+1\right)=\widehat{A}x\left(k\right)+\widehat{B}\mathsf{\Delta }u\left(k\right),$$

(11)

$$\widehat{y}\left(k\right)=\widehat{C}\widehat{x}\left(k\right),$$

(12)

where $\widehat{x}$ is the augmented state vector, $\widehat{A}$, $\widehat{B}$, and $\widehat{C}$ are the augmented state, input, and output matrices; and $\widehat{y}$ is the estimated output vector.

The MPC algorithm aims to solve the following constrained optimization problem for the augmented system:

$$\underset{\mathsf{\Delta }U}{min} J(\mathsf{\Delta }U)=\sum _{k=1}^{N_p} y_i^{T}Q{y}_i+\sum _{k=1}^{N_c} \mathsf{\Delta }{u}_i^{T}R\mathsf{\Delta }{u}_i,$$

(13)

$$\begin{array}{c}\mathsf{\Delta }{u}_{min}\le \mathsf{\Delta }u\left(k\right)\le \mathsf{\Delta }{u}_{max} \forall k\in N_c,\\ u_{min}\le u\left(k\right)\le u_{max} \forall k\in N_c,\end{array}$$

(14)

where N_p is the prediction horizon, N_c is the control horizon, and ∆u_min, ∆u_max, u_min, u_max are the constraints on the gradient and magnitude of the input signal, and ∆U represents the sequence of control input changes over the control horizon. The constrained optimization problem is typically solved using quadratic programming (QP), as it effectively identifies the active constraints. By applying the receding horizon control principle of MPC, constraints are imposed only on the initial samples of the solution.

These controllers are evaluated in a simulation environment to determine their effectiveness in optimizing vehicle dynamics and passenger comfort under varying speed conditions.

3.5. Gain Scheduling

Gain Scheduling is a control technique that dynamically adjusts the controller parameters based on the operating conditions. In the presented algorithms, the control gains are scheduled based on the longitudinal velocity of the vehicle. The presented method uses precomputed gains for various operating points and interpolates between them in real time, allowing for smooth transitions and improved vehicle handling. By adapting the control gains to the vehicle’s speed, this approach provides more adaptive behavior in dynamic driving scenarios, where fixed-gain controllers may not perform well.

4. Simulation Results

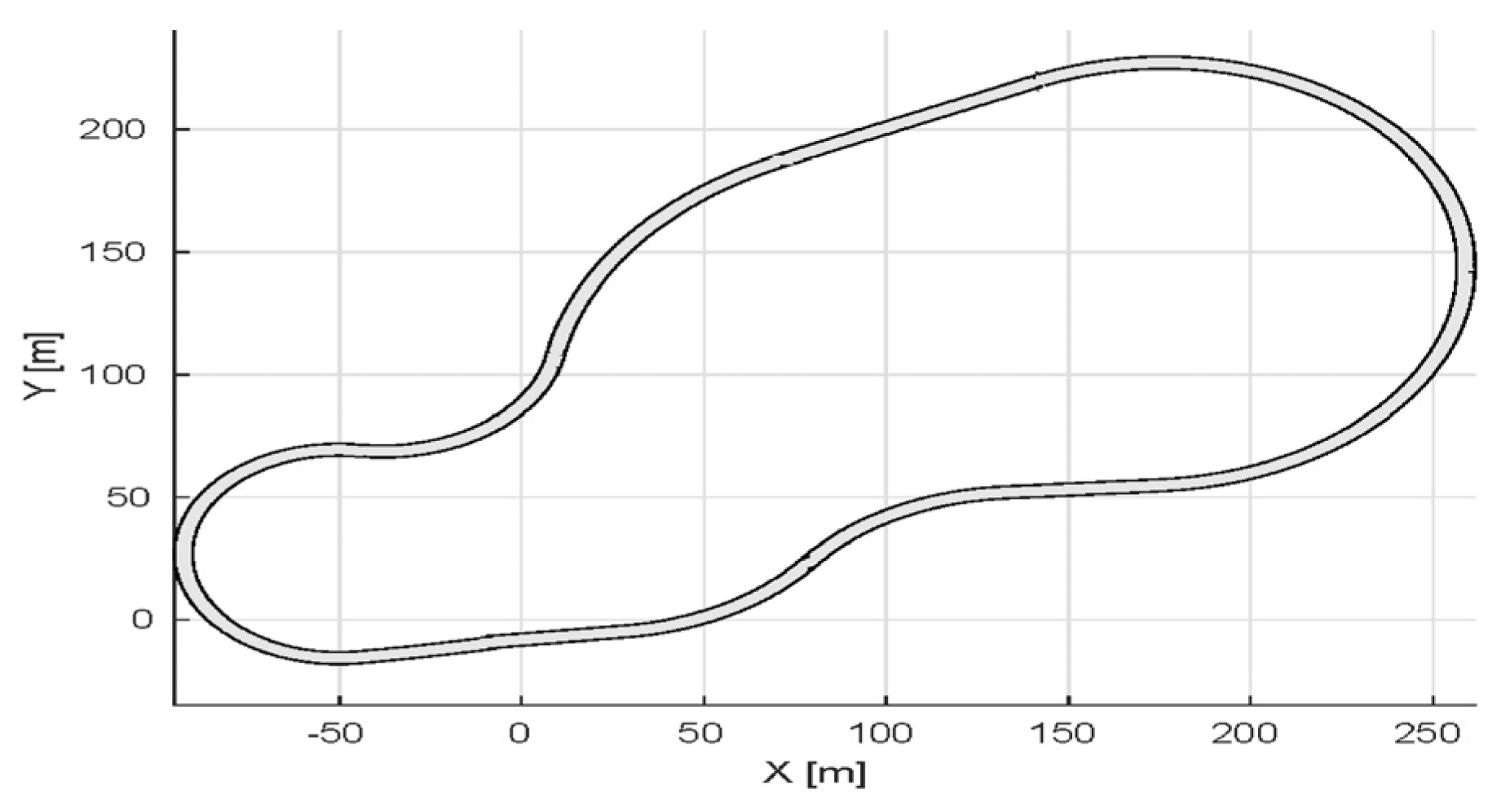
The control algorithms have been implemented in the Matlab/Simulink 2022b environment. Figure 1. illustrates the trajectory that was created using the CarMaker 11.1 software package. The simulation included various driving scenarios with speed variations between 30 km/h and 100 km/h, designed to test the controllers’ performance under dynamic conditions.

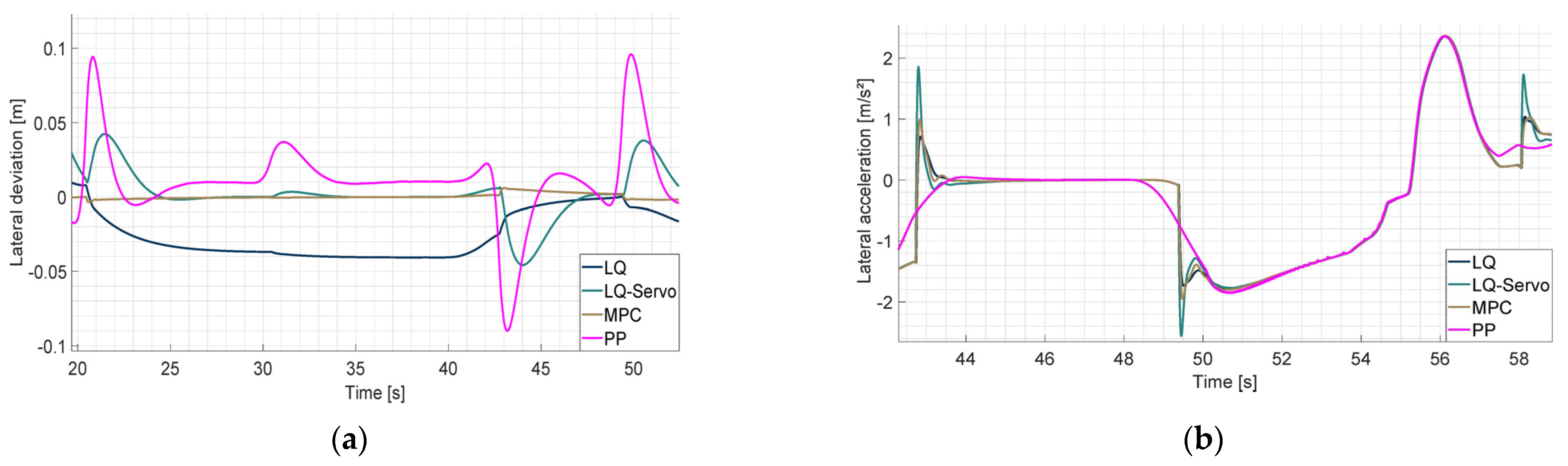
Figure 2a shows that the Pure Pursuit controller had the largest deviations, especially in sharp turns, due to the chosen lookahead distance. The LQ controller demonstrated smaller errors but lacked integrating properties for steady-state error correction. Due to its integral property, the LQ-Servo controller effectively reduced steady-state errors despite larger initial deviations. However, the initial reduction and subsequent overshoot of integrated errors can lead to a delayed response from the controller. The MPC controller showcases superior tracking accuracy due to its predictive planning capabilities.

Figure 2b shows the lateral accelerations, crucial for passenger comfort. The LQ-Servo and MPC controllers show peaks due to sudden control interventions, which quickly dissipate. The LQ and Pure Pursuit controllers maintained lower accelerations. Based on [17] and the ISO 2631 standard [18], the equivalent acceleration (a_eq) is selected as a metric for passenger comfort. The calculated a_eq values for the controllers are as follows: 0.55993 m/s² for PP, 0.58421 m/s² for LQ, 0.57213 m/s² for LQ-Servo, and 0.58357 m/s² for MPC. The data indicate that all four controllers are in the ‘slightly uncomfortable’ category with respect to the equivalent acceleration.

5. Conclusions

This paper compares three speed-dependent lateral control strategies (LQ, LQ-Servo, and MPC) and a conventional PP control regarding reference signal tracking and passenger comfort.

Considering the dynamic test track, all controllers meet the stability and comfort requirements as expected. However, as anticipated, gain scheduling improves the controller performance significantly. Considering the overall results, the MPC performs best, with negligible position errors and acceptable acceleration values. The LQ and LQ-Servo controllers have slightly larger deviations and similar lateral acceleration. The Pure Pursuit controller has the worst performance regarding tracking accuracy, especially in sharp turns, which confirms our initial assumptions.

These results show that gain scheduling significantly improves the accuracy of all controllers and suggests that MPC is a promising choice for real vehicle tests.