Parametric Study on Cellular Negative Stiffness Honeycomb Meta-Structures: Effect on the Energy Absorption Performance †
Abstract
1. Introduction
2. Methodology
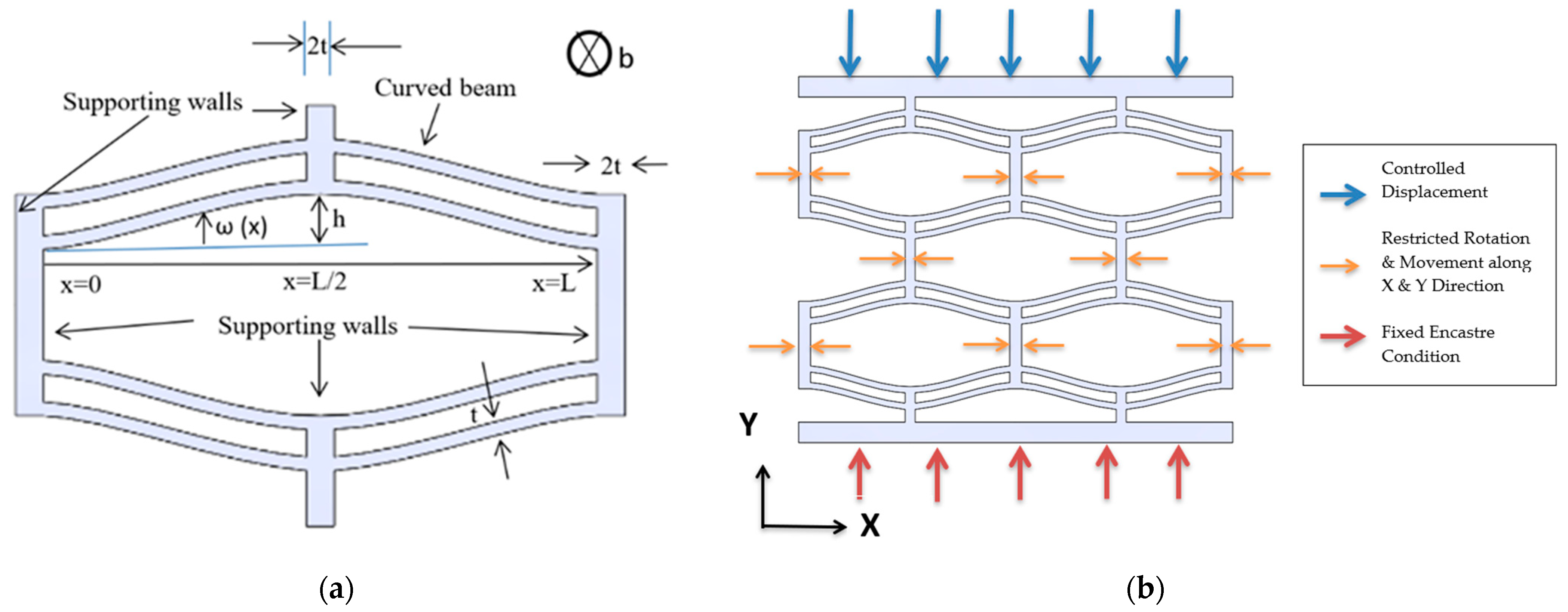
3. Structural and Design Parameters
4. Numerical Modeling
4.1. Boundary Condition
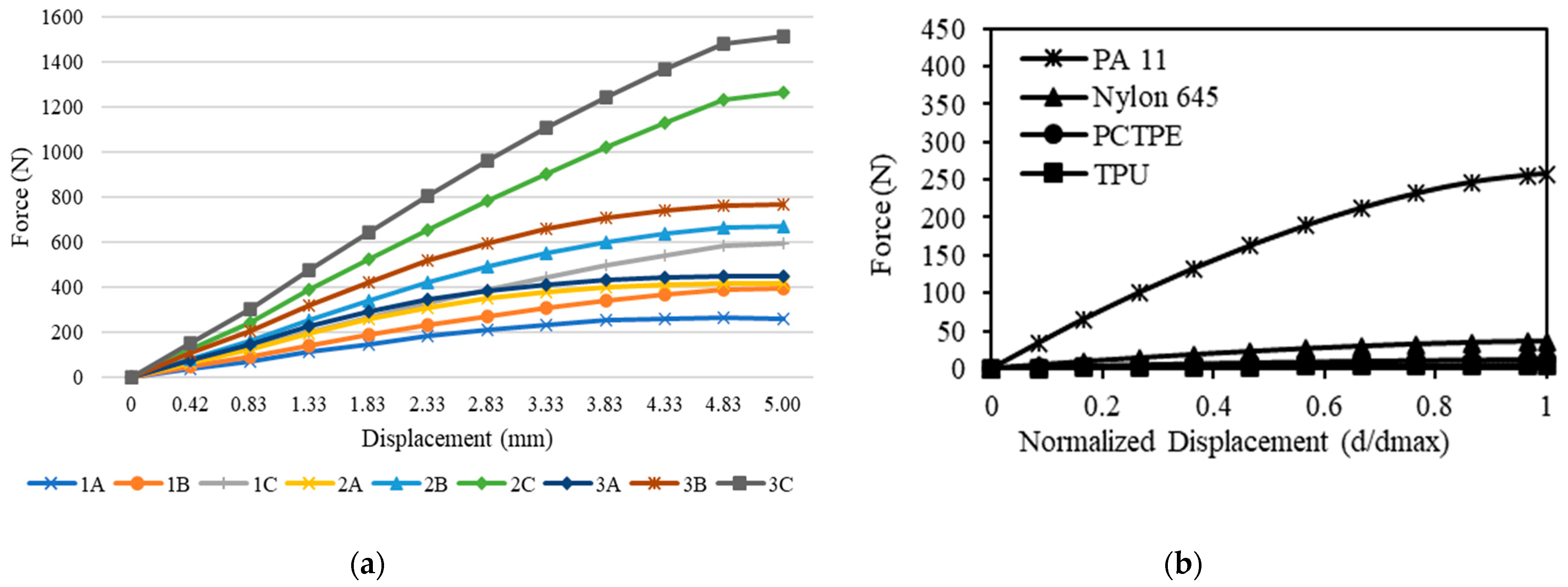
4.2. Material Properties
| Material | Polyamide-11 (PA) | TPE |
| Commercial Name | Nylon 11 | Taulman PCTPE |
| Density (Kg/m3) | 1040 | 1250 |
| Young’s Modulus (MPa) | 1582 | 73 |
| Poisson’s Ratio | 0.33 | 0.50 |
| Material | Nylon 645 | TPU |
| Commercial Name | Taulman Natural 645 Nylon | Cheetah™ |
| Density (Kg/m3) | 1300 | 1220 |
| Young’s Modulus (MPa) | 212 | 26 |
| Poisson’s Ratio | 0.42 | 0.39 |
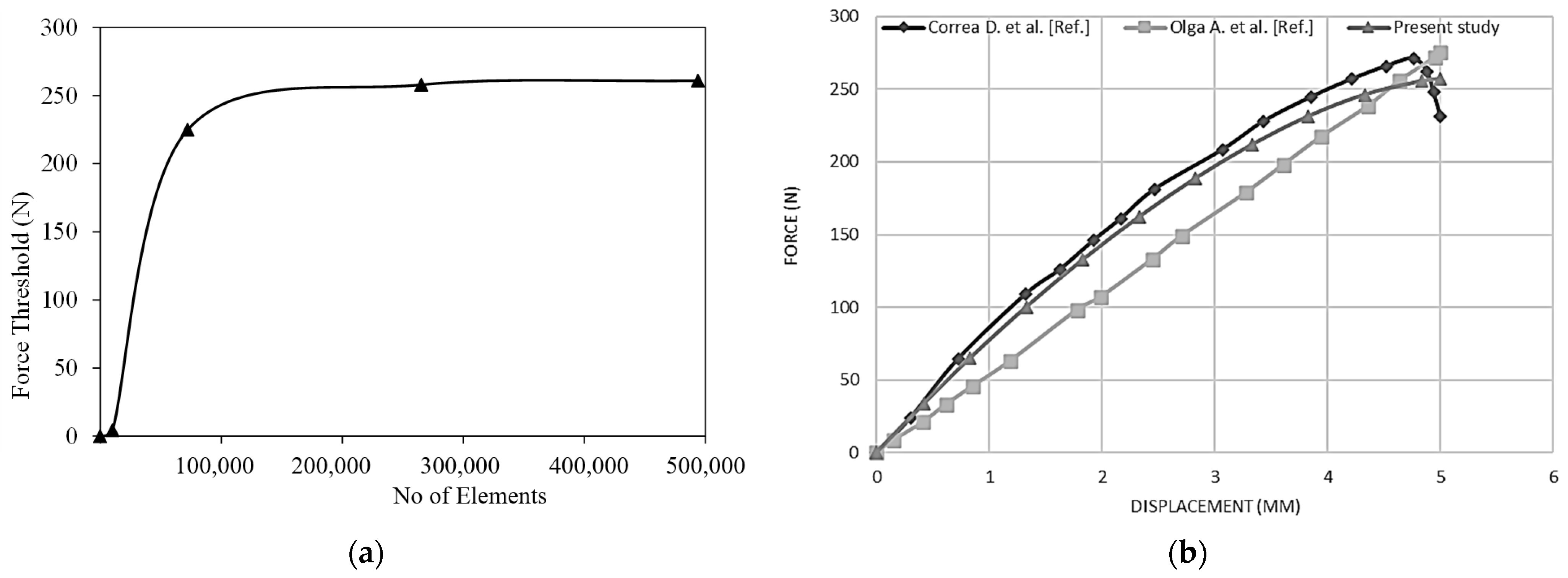
4.3. Mesh Dependency Test
5. Results
5.1. Model Verification
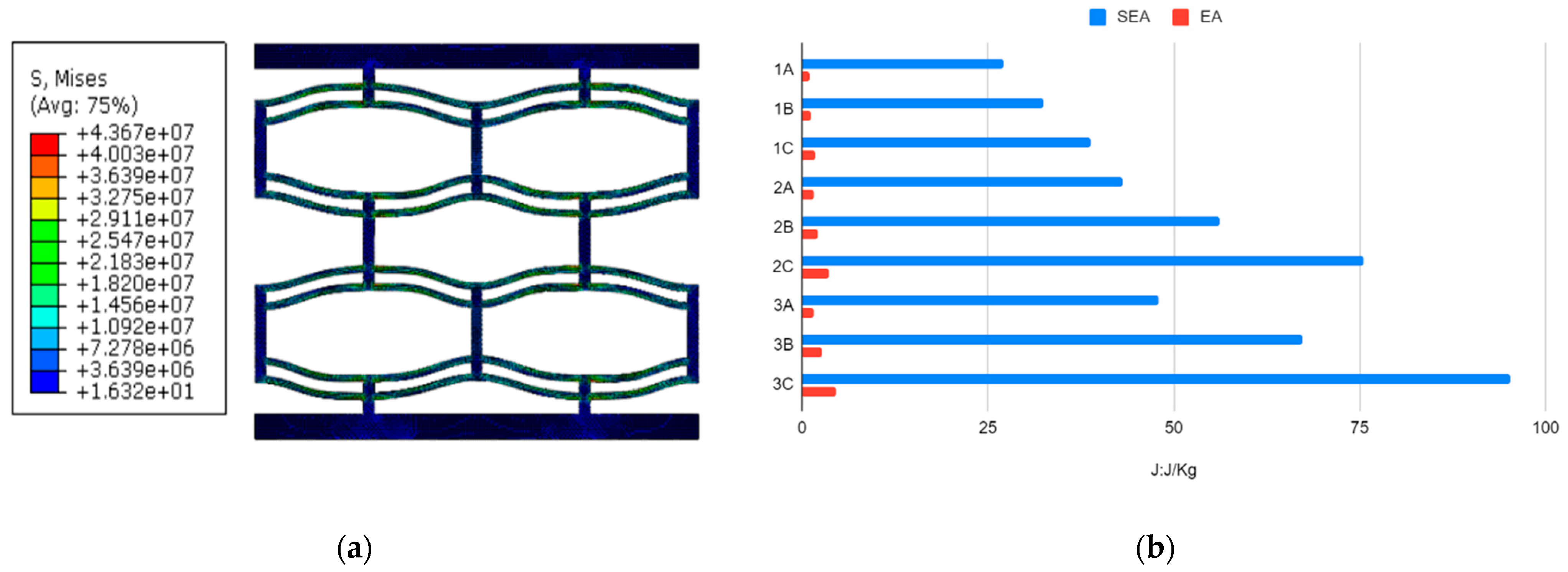
5.2. Displacement, Stress, and Energy
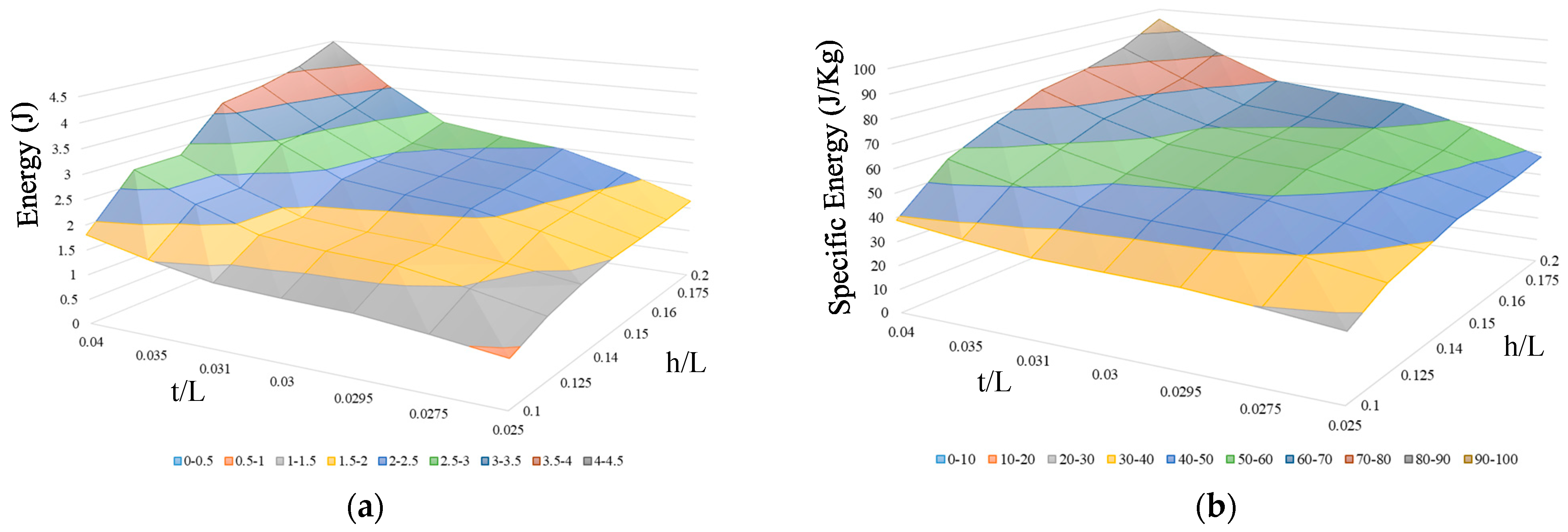
5.3. Parametric Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, W.; Reid, S.R. Metallic energy dissipating systems. Appl. Mech. Rev. 1978, 31, 277–288. [Google Scholar]
- Li, M.; Deng, Z.; Guo, H.; Liu, R.; Ding, B. Optimizing crashworthiness design of square honeycomb structure. J. Cent. South Univ. 2014, 21, 912–919. [Google Scholar] [CrossRef]
- Hassan, M.S.; Chavez, L.A.; Chou, C.; Hall, S.E.; Tseng, T.; Lin, Y. Mechanical response of shape-recovering metamaterial structures fabricated by additive manufacturing. Mater. Res. Express 2021, 8, 115801. [Google Scholar] [CrossRef]
- Regis, J.E.; Renteria, A.; Hall, S.E.; Hassan, M.S.; Marquez, C.; Lin, Y. Recent trends and innovation in additive manufacturing of soft functional materials. Materials 2021, 14, 4521. [Google Scholar] [CrossRef] [PubMed]
- Correa, D.M.; Seepersad, C.C.; Haberman, M.R. Mechanical design of negative stiffness honeycomb materials. Integr. Mater. Manuf. Innov. 2015, 4, 165–175. [Google Scholar] [CrossRef]
- Klatt, T.; Haberman, M.; Conner Seepersad, C. Selective laser sintering of negative stiffness mesostructures for recoverable, nearly-ideal shock isolation. In Proceedings of the 2013 International Solid Freeform Fabrication Symposium, University of Texas at Austin, Austin, TX, USA, 12–14 August 2013. [Google Scholar]
- Kashdan, L.; Seepersad, C.C.; Haberman, M.; Wilson, P.S. Design, fabrication, and evaluation of negative stiffness elements using SLS. Rapid Prototyp. J. 2012, 18, 194–200. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Conner Seepersad, C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Correa, D.M.; Klatt, T.; Cortes, S.; Haberman, M.; Kovar, D.; Seepersad, C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyp. J. 2015, 21, 193–200. [Google Scholar] [CrossRef]
- Mehreganian, N.; Fallah, A.S.; Sareh, P. Structural mechanics of negative stiffness honeycomb metamaterials. J. Appl. Mech. 2021, 88, 051006. [Google Scholar] [CrossRef]
- Debeau, D.A.; Seepersad, C.C.; Haberman, M.R. Impact behavior of negative stiffness honeycomb materials. J. Mater. Res. 2018, 33, 290–299. [Google Scholar] [CrossRef]
- Zhakatayev, A.; Kappassov, Z.; Varol, H.A. Analytical modeling and design of negative stiffness honeycombs. Smart Mater. Struct. 2020, 29, 045024. [Google Scholar] [CrossRef]
- Chen, S.; Wang, B.; Zhu, S.; Tan, X.; Hu, J.; Lian, X.; Wang, L.; Wu, L. A novel composite negative stiffness structure for recoverable trapping energy. Compos. Part A Appl. Sci. Manuf. 2020, 129, 105697. [Google Scholar] [CrossRef]
- Ganilova, O.A.; Low, J.J. Application of smart honeycomb structures for automotive passive safety. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 797–811. [Google Scholar] [CrossRef]
- Bonner, D.; Pellegrini, S.; Rudolph, M.; Hilbere, M. Sensitive Payload Shock Absorber; The Pennsylvania State University: University Park, PA, USA, 2016. [Google Scholar]
- Tan, X.; Chen, S.; Zhu, S.; Wang, B.; Xu, P.; Yao, K.; Sun, Y. Reusable metamaterial via inelastic instability for energy absorption. Int. J. Mech. Sci. 2019, 155, 509–517. [Google Scholar] [CrossRef]
- Tan, X.; Wang, B.; Chen, S.; Zhu, S.; Sun, Y. A novel cylindrical negative stiffness structure for shock isolation. Compos. Struct. 2019, 214, 397–405. [Google Scholar] [CrossRef]
- University of Texas at Austin New Honeycomb-Inspired Design Delivers Superior Protection from Impact. ScienceDaily 2015. Available online: www.sciencedaily.com/releases/2015/06/150615142849.htm (accessed on 6 October 2022).
- Chen, S.; Tan, X.; Hu, J.; Zhu, S.; Wang, B.; Wang, L.; Jin, Y.; Wu, L. A novel gradient negative stiffness honeycomb for recoverable energy absorption. Compos. Part B Eng. 2021, 215, 108745. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A curved-beam bistable mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Chanda, S.; Hasib, M.A.; Alam, M. Numerical analysis of recoverable Negative Stiffness Smart Structures for energy absorption in shock isolation. In Proceedings of the International Conference on Mechanical, Industrial and Energy Engineering 2020, Khulna, Bangladesh, 19–21 December 2020. [Google Scholar]
- PCTPE Specifications. Available online: https://filament2print.com/en/nylon-pa/610-4465-taulman-pctpe.html (accessed on 25 May 2022).
- Nylon 645 Specifications. Available online: https://re3d.zendesk.com/hc/en-us/articles/360039399311-Taulman-Nylon-645 (accessed on 25 May 2022).
- Hao, G.; Mullins, J. On the comprehensive static characteristic analysis of a translational bistable mechanism. Proc. Inst. Mech. Eng. Part C 2016, 230, 3803–3817. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanda, S.; Hasib, A.; Rahman, A.; Wadud, M.A. Parametric Study on Cellular Negative Stiffness Honeycomb Meta-Structures: Effect on the Energy Absorption Performance. Eng. Proc. 2024, 76, 51. https://doi.org/10.3390/engproc2024076051
Chanda S, Hasib A, Rahman A, Wadud MA. Parametric Study on Cellular Negative Stiffness Honeycomb Meta-Structures: Effect on the Energy Absorption Performance. Engineering Proceedings. 2024; 76(1):51. https://doi.org/10.3390/engproc2024076051
Chicago/Turabian StyleChanda, Sumit, Abdul Hasib, Arafater Rahman, and M A Wadud. 2024. "Parametric Study on Cellular Negative Stiffness Honeycomb Meta-Structures: Effect on the Energy Absorption Performance" Engineering Proceedings 76, no. 1: 51. https://doi.org/10.3390/engproc2024076051
APA StyleChanda, S., Hasib, A., Rahman, A., & Wadud, M. A. (2024). Parametric Study on Cellular Negative Stiffness Honeycomb Meta-Structures: Effect on the Energy Absorption Performance. Engineering Proceedings, 76(1), 51. https://doi.org/10.3390/engproc2024076051







