Abstract
Many actuating and electro-mechanical devices are driven by DC motors. Gear trains are used to amplify the torque in these motors. They are used in a wide variety of automotives, robotics, and automation applications. However, gears are prone to backlash during their operation of amplifying torques of electromehanical drives. This results in the disengagement of gear teeth when the rotation is reversed. These effects give rise to positional inaccuracies and poor control of the system. This proposed Drive-Anti Drive mechanism is used to track the system’s desired response in the presence of backlash in such cases. The Drive-Anti Drive mechanism consists of two motors rotating in opposite directions. Both the drive and the anti-drive are the DC Machines. The simulation results of the proposed scheme on the tracking control of Inverted Pendulum have been presented. Simulation results depict that the utilization of Drive-Anti Drive system has achieved the target outcome in less than 20 s. However, the target tracking of a system with the utilization of single drives takes 40 s. Setting response of an inverted pendulum is approximately twice as efficient with the utilization of the Drive-Anti Drive mechanism. This approach has been able to effectively track the target in the presence of backlash with the utilization of the Drive-Anti Drive mechanism.
1. Introduction
Backlash refers to the undesired vibration or movement in electromechanical systems that is brought about by the clearance or play between the connected components. Numerous applications, such as gear transmissions, CNC machines, and robotics, might be adversely affected by this phenomenon, which could lead to inefficiencies in precision, accuracy, stability, and overall performance. To improve system performance by reducing mistakes, it is crucial to resolve this issue immediately. In an attempt to mitigate the negative effects of backlash, scholars have proposed a plethora of methods. Concerns about backlash continue to be high in the field of electromechanical systems, where they have a significant impact on the reliability and precision of these systems. On an electromechanical test bench, which had a DC motor supplying a mechanical load via a reducer component, Merzouki et al. [1] conducted both theoretical and practical investigations. Using a fault detection and isolation strategy, a new method was suggested for electromechanical testing that could detect and differentiate between unwanted and useful backlash occurrences. In order to foresee and reduce the disruptive torque that occurs inside an electromechanical system’s dead zone, Mohamed et al. [2] created a feedforward control method. Extending model structures to bond graphs was shown to be a very successful approach. By applying the outcomes of simulations to an electromechanical actuator, theoretical concepts were brought to light. Tararykin and Apolonskiy [3] set out to investigate electric motors with backlash in their mechanical components to find out what causes automatic oscillation and the reduction of transient process quality. This was accomplished by investigating the nonlinear electric drive system’s dynamics using frequency analysis methods. The authors specifically advocated for the use of a proportional-integral (PI) position controller that includes a switchable integral component. They also suggested adding extra stabilization feedback to make up for the electric motor’s and the operational unit’s different angular displacements as inputs to the current controller.
Backlash refers to the undesired vibration or movement in electromechanical systems that is brought about by the clearance or play between the connected components. Numerous applications, such as gear transmissions, CNC machines, and robotics, might be adversely affected by this phenomenon, which could lead to inefficiencies in precision, accuracy, stability, and overall performance. To improve system performance by reducing mistakes, it is crucial to resolve this issue immediately. In an attempt to mitigate the negative effects of backlash, scholars have proposed a plethora of methods. Concerns about backlash continue to be high in the field of electromechanical systems, where they have a significant impact on the reliability and precision of these systems. On an electromechanical test bench, which had a DC motor supplying a mechanical load via a reducer component, Merzouki et al. [1] conducted both theoretical and practical investigations. Using a fault detection and isolation strategy, a new method was suggested for electromechanical testing that could detect and differentiate between unwanted and useful backlash occurrences. In order to foresee and reduce the disruptive torque that occurs inside an electromechanical system’s dead zone, Mohamed et al. [2] created a feed forward control method. Extending model structures to bond graphs was shown to be a very successful approach. By applying the outcomes of simulations to an electromechanical actuator, theoretical concepts were brought to light. Tararykin and Apolonskiy [3] set out to investigate electric motors with backlash in their mechanical components to find out what causes automatic oscillation and the reduction of transient process quality. This was accomplished by investigating the nonlinear electric drive system’s dynamics using frequency analysis methods. The authors specifically advocated for the use of a proportional-integral (PI) position controller that includes a switchable integral component. They also suggested adding extra stabilized feedback to make up for the electric motor’s and the operational unit’s different angular displacements as inputs to the current controller.
The traditional electric drive’s astatic servo mechanism was thoroughly examined by Tararykin and Apolonskiy [4]. To accurately describe the cascade’s current, voltage, and position control, they used the harmonic linearization method. To mitigate the impacts of backlash, researchers refined methods for responding to sudden kinematic changes by modifying the properties of integrated components in the primary position control loop.
Backlash Inverse (BI) compensation is a common method for electromechanical actuators (EMA) to reduce the effect of backlash. Nevertheless, conventional BI fails to address intricate situations and reduces the effectiveness of servo systems since it is limited to certain circumstances like substantial system dampening and zero load torque. To solve this issue, Cao et al. [5] used active disturbance rejection in their torque-type bidirectional controller for electromagnetic actuators (EMAs). A dead zone and a stiff coupling between two masses were first modelled in an attempt to recreate the EMA.
Electric actuators were the subject of study by Li [6], who worked on electric actuators while considering nonlinear characteristics like friction and gear gap. The nonlinear properties of every part were investigated in detail using MATLAB/Simulink models. Different parts and locations showed different nonlinear behaviors according to the results. Since these parameters significantly impact the output signal, it is critical to note that the dead zone area of the gap and friction should not exceed two percent of the input signal. In addition, the gearbox construction’s matching rigidity must be at least 1 Nm/rad to ensure there is no dead zone within the gap. Sun et al. [7] presented an observer-based method to solve the problem of backlash in servo systems in their research. Prior to controller design, this method assessed system states and vibration torque. Ershov et al. [8] dealt with the stabilization issue of a two-mass system that had a kinematic gearbox backlash and motor current constraint. This model took internal viscous friction as a parameter. Achieving very efficient tracking control in electromechanical servo systems was the primary emphasis of the work carried out by Baiet al. [9], which is based on neural network architecture
Yuan et al. [10] suggested a reliable adaptive precision motion controller to handle unknown actuator backlash and uncertainties in tank horizontal actuators. A continuous nonlinear robust law and adaptive feedforward compensation were included into the controller to handle modelling uncertainties, including unmodeled disturbances and parameter uncertainties. When dealing with model flaws and uncertain actuator backlash, Yuan et al. [11] tackled the problem of achieving accurate motion control for motor servo systems. Using a combination of synthetic adaptive rules and a continuous nonlinear robust term, the controller effectively dealt with parameter uncertainties and disturbances in the system. Vered et al. [12] looked at the possibility of using a digital twin to update a feedback controller. A position-controlled dynamical system with a time-varying nonlinear element was used in the simulations that were run to carry out this inquiry. A DC motor, which was a part of the feedback control system, was used to move a three-dimensional structure. The gap angle changed over time due to factors including wear, and this displacement was impacted by backlash.
This study develops a mathematical model and technique to eliminate unwanted noise in electromechanical drives, particularly when these drives experience changes in torque. The technique presents a novel state feedback controller for dual drive mechanism for dynamic systems, such as an inverted pendulum, to achieve optimal performance by canceling out various noises, including backlash and frictional torques. Error dynamics are calculated and integrated into the system to ensure precise control and stability.
2. Drive Anti-Drive Mechanism
The drive mechanism is used to compensate for the backlash. The Drive-Anti Drive mechanism utilizes two drives by applying torques in opposite directions. Therefore, the torques must be regulated for achieving optimum target tracking applications. This mechanism works on the principle of applying constant torque in the opposite direction to ensure mesh in the gear trains remain intact. Whenever the Drive undergoes change in direction, Anti-Drive provides the torque in the opposite direction to compensate for the backlash. The constant torque can be attained by converting regulated current into the regulated torque. Regulated current has been achieved by utilizing the technique mentioned in [13]. Since torque is directly proportional to the current, torque regulation can easily be achieved.
where represent armature current of Drive-1 and Drive-2, respectively. The Drive-Anti Drive mechanism drives the load in the direction of greater torque. One of the machines acts as a motor, whereas the other one acts as a Generator. Torque is applied in opposite directions to both drives at all times to ensure positive coupling of gears, as shown in Figure 1. Resultant torque acting on load depends on the difference between driving torques and drives the load in the direction of greater torque as per Equation (3) below.
Compensation of backlash requires maintaining a minimum level of grabbing torque, thereby keeping the gears in contact, as given by Equation (4) below:
Equation (5) represents the mechanical dynamics of the motor and load. It shows that the net driving torque τd is equal to the load torque τl plus the inertial and the frictional torques.
The constants J and B are the moment of inertia of the rotating mass and friction coefficient.
Grabbing torque coefficient is defined by bg
The Drive-Anti Drive dynamical model results in the following differential equation, given by Equation (7) below.
Here, bg represents an additional friction coefficient because of grabbing torque. Putting the value of bg in Equation (8) above results in:
The mechanism has been driven by the drive and the opposing torques. The net opposing torque is equivalent to the sum of all friction and grabbing torques.
where opp represents the net opposing torque.
Net opposing torque is given by:


Figure 1.
Drive Anti-Drive Dynamic Model.
3. Simulation of Proposed Scheme on Inverted Pendulum
This section focuses on the simulation of the proposed scheme on a pendulum. The pendulum changes direction continuously so it is the best illustrating example for showing backlash elimination whenever the drive undergoes a change in direction. The pendulum has been driven through the Drive-Anti Drive mechanism. Torque has been applied to both the drives in the opposite directions, as shown in Figure 1.
Dynamical Modeling of Pendulum
A weight suspended from a fixed support makes a simple pendulum, which keeps on oscillating all the time. Displacing the pendulum from its equilibrium position will accelerate the pendulum to follow a to and fro motion. Since the pendulum keeps on oscillating back and forth, is the inertial force and is the rational force; the component of force acts because of acceleration due to gravity, as shown in the Figure 2. As per Newton’s second law of motion, force acting on the pendulum is equal to the product of the mass of the pendulum and its acceleration. The gravitational function is dependent on angular velocity, as conducted by [14].
where is the mass of strings, is the length, and is the acceleration due to gravity. Frictional forces act in the direction opposite to the acting force, as shown in Figure 2. Frictional forces are proportional to angular velocity.
The differential equation is further reduced as:
For developing a state space model of the given system, angular position and angular velocity are taken as state variables.
The state space of the inverted pendulum driven by the Drive-Anti Drive model is given below. The output of the system has been taken as angular position, and is given as below:
The swinging pendulum is taken as the load. Load torque changes its magnitude and direction all the time because of the action of gravity.
b is the friction coefficient. τgkgω is the additional frictional coefficient because of the grabbing torque. Driving torque has been applied at the input. This scheme has inherent nonlinear terms, which consist of load torque and additional friction coefficient because of grabbing torque. There must be some structural property of the system that allows us to cancel out nonlinearities. Nonlinear term α(x) can be cancelled out if the control input and nonlinearities appear as a sum u + α(x), as conducted by Khalil [14].
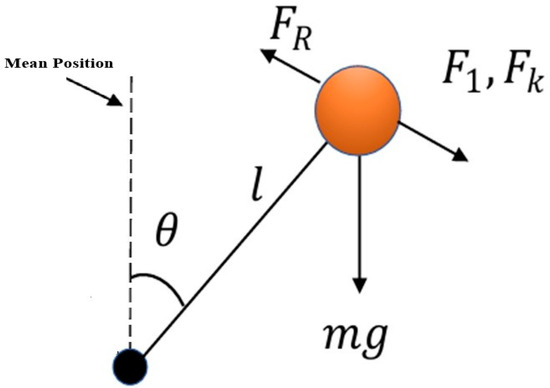

Figure 2.
Free body diagram of pendulum in presence of friction.
Some systems, where nonlinear terms appear in the product form, result in a complex scenario. Coping with the above-mentioned issues, the singularity has been checked for nonlinear product terms. Cancellation of nonlinear terms in the case of singular systems is not possible. Cancellation of non-linearity in every case is not so easy. Once nonlinear disturbing forces get cancelled out, linearizing feedback can be established. For stabilization, a suitable feedback controller must be designed, which places (A-BK) roots in LHP. It is desired that output y(t) tracks reference signal r(t) with bounded derivatives of r(t).
Error states of the system for achieving the desired trajectory can be defined as follows:
Error dynamics can be obtained as follows:
Linearizing feedback can be obtained by cancelling out nonlinearities:
Stabilizing feedback has been achieved by selecting certain gain K, which assigns eigenvalues of (A-BK) in the Left Half Plane.
For this particular set of simulations, the output signal y(t) has to track reference signal . The pendulum has a to and fro motion. For the subsequent analysis, two positions are considered.
- Mean Position: Here, the pendulum experiences maximum velocity, which pushes it to attain the extreme position. The angular velocity is maximum at the mean position. Thus, at the mean position, kinetic energy is maximized. Minimum torque is applied at the input since angular displacement has been reduced to zero.
- Extreme Position: The pendulum has maximum potential energy and zero kinetic 173 energy as the pendulum stops here for a certain amount of time. Driving Torque is maximum at the 174 extreme position since it forces the bob to displace from the mean position.
Pendulum position plays a vital role in changing torques applied at the input. It is observed here that the torque requirement varies continuously with the pendulum position. The pendulum starts swinging from its mean position to an extreme position. When a pendulum is displaced to the right, drive-2 torque is greater than drive-1 torque. Then, at this point, it attains maximum potential energy, and the pendulum swings back to its mean position under the action of gravity. At the mean position, its velocity attains a maximum value, thus it does not stop at the mean position. Kinetic energy converts into potential energy, which forces the pendulum to move towards the left (the other extreme position). Once again, the pendulum does not stop swinging at the extreme position; it keeps continuing back and forth from the left extreme position to the mean extreme position, then to right extreme position and then back to mean position. Finally, it returns to left extreme position and so on. Hence, this cycle continues. In one complete swing of the pendulum, the pendulum attains the following four positions:
- Mean position to left extreme position.
- Left extreme position to mean position.
- Mean position to right extreme position.
- Right extreme position to mean position.
Mean position, as depicted in Figure 2, refers to “0”. When displaced to left, Left extreme position refers to “−1”. Right extreme position refers to “+1”. Displacement of the pendulum has been taken as positive when it is displaced from the mean position to right extreme position. Left displacement will be taken as negative. An interesting fact can be observed here: both drives are changing their roles. The backlash has been eliminated by applying torques to both drives in opposite directions. At extreme positions, the pendulum rests, i.e., angular velocity has reduced to zero, so frictional losses are minimized. Losses increase when the pendulum starts oscillating from the left extreme position to the mean position. Losses increase when the pendulum starts oscillating from the right extreme position to the mean position.
The pendulum was required to follow the reference trajectory:
This state feedback controller tracks reference output at every instant of time. The error of the system has converged to zero in a finite time.
The pendulum has achieved asymptotic stability because the error has converged to zero in a finite time. The output of the pendulum has started tracking reference output in a finite time:
The backlash has been eliminated successfully for swinging loads. Net driving torque that helps to maintain the positional accuracy is depiced in Figure 3. Position and Error graphs with the utilization of the Drive-Anti Drive mechanism are shown in the left half of Figure 4. Comparison of error function by utilizing single Drive and Drive-Anti Drive are shown in the right half of Figure 4.
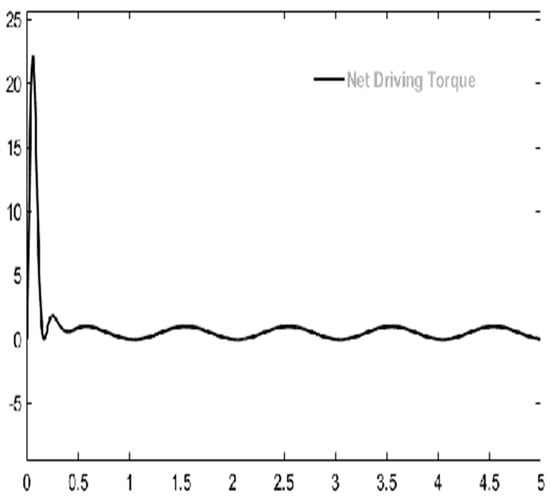
Figure 3.
Net Driving Torque of D-AD.
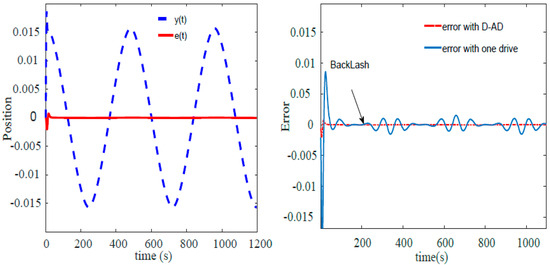
Figure 4.
Left: Position and Error of pendulum. Right: Comparison of error with D-AD and One-Drive.
4. Discussion
In the right side of Figure 4, the system’s error graphs are compared for two cases:
- (1)
- When driven with a single drive.
- (2)
- When driven with a drive-anti-drive mechanism.
The performance of both systems was evaluated. The red graph depicts the error graph for the Drive-Anti Drive mechanism, while the blue graph shows the error graph for the single drive. The red line achieves asymptotic stability quickly when compared to the blue line. The system performs significantly better with the Drive-Anti Drive mechanism, achieving a steady-state response much more quickly compared to the single drive. Settling time for the Drive-Anti Drive mechanism comes out to 20 sec, whereas settling time for single drives is 40 s. Additionally, overshoots and noise parameters are considerably higher when the system is subjected to changes in torque with a single drive. These surges can be seen from these performance metrics, indicating improved performance and better tracking control in the system, especially in dynamic conditions with frequent perturbations. The Drive-aAnti Drive mechanism enhances the system’s ability to quickly reach a steady-state response and reduces the impact of overshoots and noise when torque changes occur.
5. Conclusions
The current research focused on the compensation of the backlash in electromechanical drives by utilizing two unidirectional drives. The proposed technique, using two unidirectional drives, has been implemented in the classical inverted pendulum problem. The results of this study exhibit successful elimination of the backlash with perfect target tracking. Anti-Drive is continuously providing torque for maintaining the mesh of the gear. Mechanical losses are maximum at the mean position of the pendulum, whereas mechanical losses are reduced to zero at the extreme positions. More losses have been added into the Drive-Anti Drive mechanism. Target tracking for single drive and Drive-Anti Drive has been compared. Results show that the target tracking by the Drive-Anti Drive mechanism has improved performance when compared to Single Drives.
Author Contributions
Conceptualization, A.A.A. and U.S.K.; methodology, A.A.A. and U.S.K.; software, A.A.A.; validation, A.A.A. and U.S.K.; formal analysis, A.A.A. and U.S.K.; investigation, A.A.A. and U.S.K.; writing—original draft preparation, A.A.A.; writing review and editing A.A.A. and U.S.K.; visualization, A.A.A. and U.S.K.; supervision U.S.K.; project administration, A.A.A. and U.S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| D-AD | Drive-Anti Drive Mechanism |
| Opposing Torque | |
| Frictional Torque | |
| Grabbing Torque | |
| Load Torque | |
| Driving Torque | |
| J | Moment of Inertia of Motor |
| B | Friction Coefficient |
| Error 1 | |
| Error 2 |
References
- Merzouki, R.; Medjaher, K.; Djeziri, M.A.; Ould-Bouamama, B. Backlash fault detection in mechatronic system. Mechatronics 2007, 17, 299–310. [Google Scholar] [CrossRef]
- Mohamed, A.; Abederrazek, L. The feedforward control of mechatronic system with backlash. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–7. [Google Scholar]
- Tararykin, S.V.; Apolonskiy, V.V. Compensating the Influence of Backlash in Highly Rigid Kinematic Transmission of Electromechanical Tracking Systems. In Proceedings of the 2022 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 16–20 May 2022; pp. 760–765. [Google Scholar]
- Tararykin, S.V.; Apolonskiy, V.V. Controlling a Servo Drive with Backlash in High-Rigidity Power Transmission. Russ. Electr. Eng. 2022, 93, 16–25. [Google Scholar] [CrossRef]
- Cao, J.; Li, Y.; Zhang, X.; Yang, J.; Fan, W. Torque-Type Backlash Inverse Control for an Electromechanical Actuator with Active Disturbance Rejection. IEEE Access 2023, 11, 108688–108696. [Google Scholar] [CrossRef]
- Li, H. Nonlinear control method of electromechanical actuator using genetic algorithm. Int. J. Mechatron. Appl. Mech. 2020, 8, 182–189. [Google Scholar]
- Sun, G.; Zhao, J.; Chen, Q. Observer-based compensation control of servo systems with backlash. Asian J. Control 2021, 23, 499–512. [Google Scholar] [CrossRef]
- Ershov, K.K.; Blagodarnii, N.S.; Kundyukov, O.A. Research of Methods for Stabilizing the Position of a Two-Mass Electromechanical System with Backlash and Motor Current Limitation. In Proceedings of the 2023 Seminar on Electrical Engineering, Automation & Control Systems, Theory and Practical Applications (EEACS), Saint Petersburg, Russia, 23–25 November 2023; pp. 87–90. [Google Scholar]
- Bai, Y.; Hu, J.; Yao, J. Adaptive neural network output feedback robust control of electromechanical servo system with backlash compensation and disturbance rejection. Mechatronics 2022, 84, 102794. [Google Scholar] [CrossRef]
- Yuan, S.-S.; Deng, W.-X.; Yao, J.-Y.; Yang, G.-L. Robust adaptive precision motion control of tank horizontal stabilizer based on unknown actuator backlash compensation. Def. Technol. 2023, 20, 72–83. [Google Scholar] [CrossRef]
- Yuan, S.; Deng, W.; Liang, X.; Yao, J.; Yang, G. Nonlinear robust adaptive precision motion control of motor servo systems with unknown actuator backlash compensation. ISA Trans. 2023, 137, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Vered, Y.; Elliott, S.J. The use of digital twins to remotely update feedback controllers for the motion control of nonlinear dynamic systems. Mech. Syst. Signal Process. 2023, 185, 109770. [Google Scholar] [CrossRef]
- Mamani, G.; Becedas, J.; Feliu, V. Robust Position Control of a DC Motor by Sliding Mode. In Proceedings of the Emerging Trends in Technological Innovation, First IFIP WG 5.5/SOCOLNET Doctoral Conference on Computing, Electrical and Industrial Systems, DoCEIS 2010, Costa de Caparica, Portugal, 22–24 February 2010; Volume 314, ISBN 978-3-642-11627-8. [Google Scholar]
- Khalil, H.K.; Hall, P.; River, U.S. Linear Systems; Routledge: England, UK, 2019; pp. 46–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).