Abstract
Water management is vital for building an adaptive and resilient society. Water demand forecasting aids water management by learning the underlying relationship between consumption and governing variables for optimal supply. In this paper, we propose a week-ahead hourly water demand forecasting technique based on deep learning (DL) utilizing an encoded representation of historical supply data and influencing exogenous variables for a District Metered Area (DMA). We deploy a CNN model with and without attention and evaluate the model’s ability to forecast the supply for different DMAs with varying characteristics. The performances are quantitatively and qualitatively compared against a baseline LSTM.
1. Introduction
Water is one of the primary natural resources and has been an integral part of shaping the current world as we know it. The need for access to water has had significant historical importance and prevails as a key challenge, as instances of water shortage are on the rise with climate change, urbanization, and changing demographics. With the drying up of lakes and riverbeds, unpredictable and extreme weather conditions, depleting groundwater levels, and increasing consumer needs (residential, agricultural, and industrial), water demand management has come to prominence [1]. District Metered Areas (DMAs) are a critical concept that enables the strategic management of utility supply areas that allow for efficient monitoring of supplied and consumed resources. The advent of smart meters provides access to data at a larger quantity and quality, and has enabled a deeper understanding of consumer behavior, adding to the ability to better manage water as a resource through techniques such as forecasting.
Time series forecasting is a regression task traditionally achieved through statistical methods, and has witnessed a significant shift towards machine learning (ML) and deep learning (DL) models in the past decade [2]. This transition is attributed to their capacity to model nonlinear functions and capture intricate patterns within data. DL-based forecasting methodologies have showcased remarkable performance across diverse domains, including utility demand forecasting [3]. An emerging approach combines advances in signal processing with DL techniques to facilitate efficient modeling of complex time series data from time-frequency representation for forecasting. These representations obtained as a consequence of the Continuous Wavelet Transform (CWT) technique are scalograms, which are analogous to an image where the coefficients are depicted in time and scale dimensions, enabling multi-resolution feature representation of the time series [4]. These multi-resolution features enable the leveraging of established DL techniques such as CNNs for the downstream objective of forecasting.
In this research, we evaluate a DL-based methodology aimed at multi-step-ahead forecasting of water demand within DMAs with an approach that encodes historical data into a time-frequency representation. Furthermore, we investigate the efficacy of integrating self-attention mechanisms within the model architecture to better capture the nuanced relationships between consumption behavior and exogenous variables. Finally, we conduct a comparative analysis, assessing the performance of our proposed model against baseline LSTM networks.
2. Materials and Methods
Let represent the time series data encapsulating the hourly water supplied (L/s) to DMA with each DMA concerning different consumer characteristics along with the relevant weather data . The dataset spans 117 weeks from 1 January 2021 to 31 March 2023. The water supply data and the weather data are analyzed for temporal irregularities (such as daylight savings) and are adjusted to be temporally consistent. For each DMA, a normalized weekly consumption profile with a zero-centered mean is computed. Statistical outliers and missing values within the dataset are addressed through rescaling and mean shifting of the identified consumption values, aligning them with the respective minimum, maximum, and mean values of each week in .
For the task of forecasting at time , where signifies the prediction horizon, we partition into weekly samples denoted as , with each sample spanning from Monday to Sunday, where Each sample constitutes a set of consumption feature vectors represented as where . The vector encapsulates historical day-wise consumption data for a week, such that at time , . Analogously, we derive the set of exogenous weather features denoted as with representing the weather conditions during the prediction horizon at time . The ambient temperature, holiday data, hour of the day, and day of the week during the prediction horizon are recognized as potential exogenous variables.
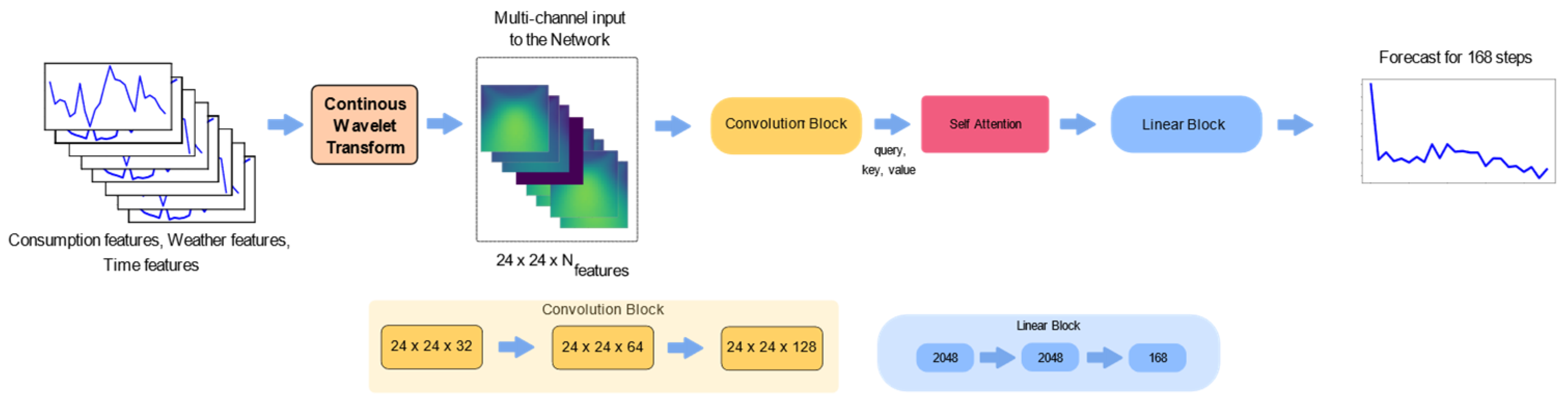
To forecast for we adopt and adapt a deep learning model [5] with a convolution back-bone to process an image-like representation of time series features vectors. Let be the set of input feature vectors, where is the number of features. The input features are identified through correlational and statistical analysis for each DMA. Through CWT, each feature in is encoded as scalograms to obtain a multi-dimensional representation and are consequently concatenated to produce a multi-channel image-like representation of dimension which acts as an input the DL model . The architecture is modified, as seen in Figure 1, with an addition of a self-attention layer between the convolution and linear blocks and the ability to enable the model to regulate weights in the latent space based on feature importance. The dataset is divided into training and testing data in the ratio 80:20, and the training dataset is further subdivided into training and validation datasets. The model is tuned for hyperparameters and is trained with a learning rate of 0.001, MSE loss function, and a batch size of 64 until convergence.
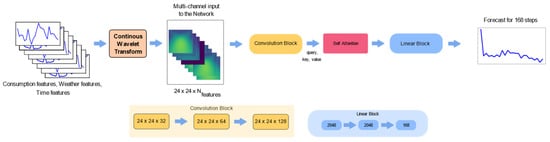
Figure 1.
Wavelet-based forecasting model , modified with self-attention layer.
3. Results
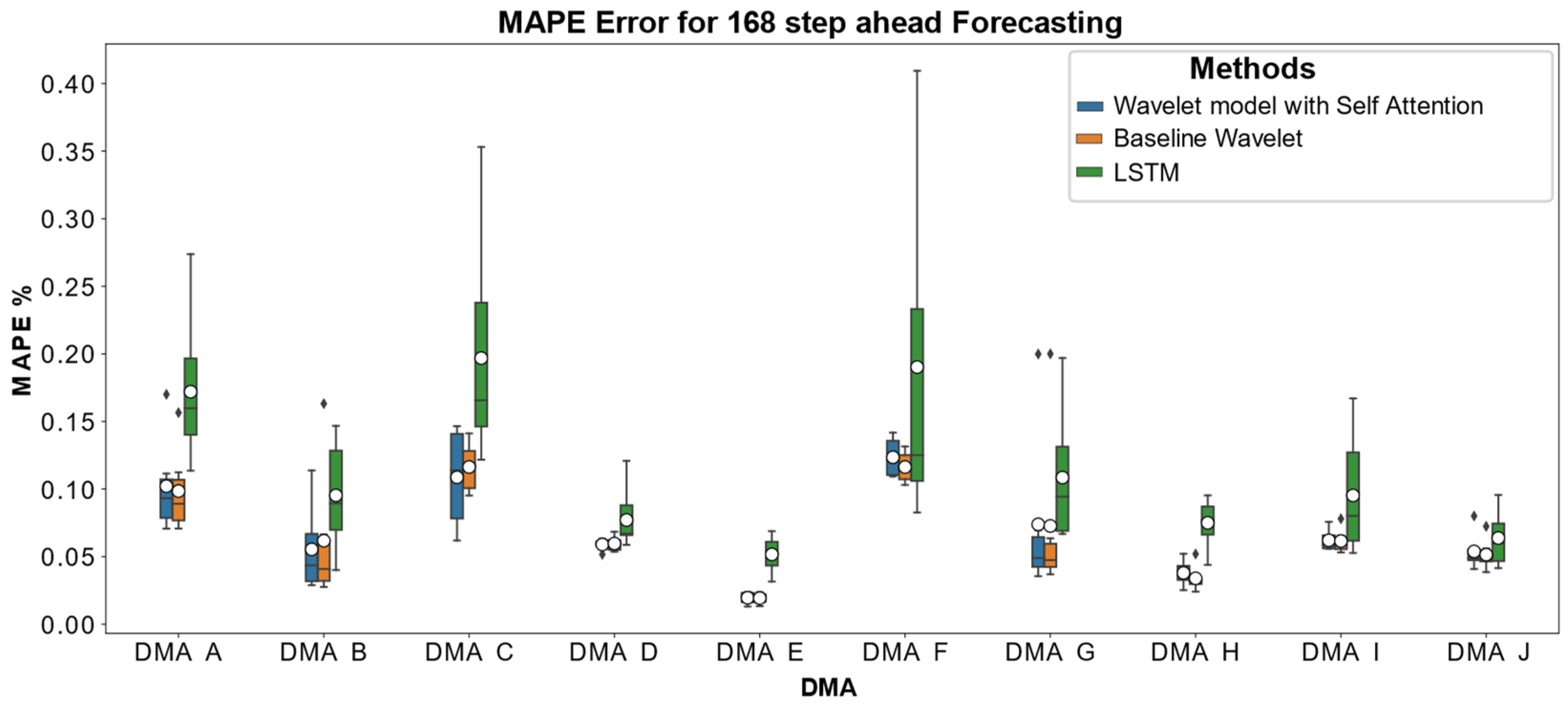
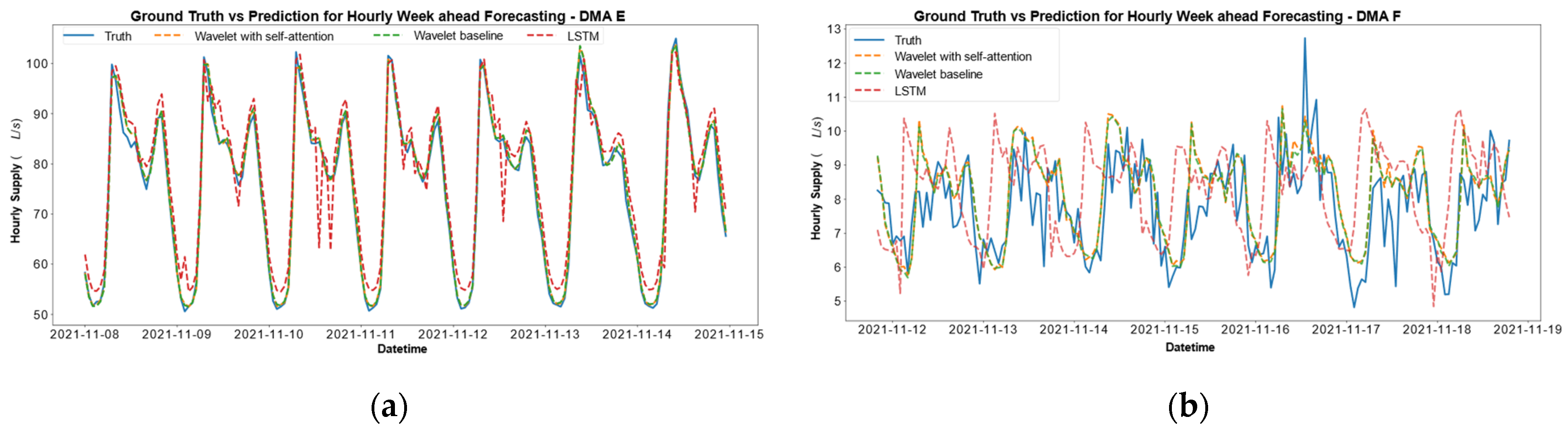
The adopted wavelet-based DL method for forecasting is utilized to analyze the impact of preprocessing steps, and features. While augmentation of the dataset to enrich the number of training samples did not impact the forecasting performance, the approach of filling in missing data through the mean-adjusted weekly load profile shows a significant increase in forecasting performance. After curating the model, the quantitative forecasting performance of each model is compared across different DMAs in Figure 2. As a baseline to enable comparison, an LSTM is also used for forecasting. The results are also qualitatively analyzed by selecting the two DMAs with the most and least MAPE metrics to understand the nuances of the different models learning capacities. The qualitative plots are visualized in Figure 3.
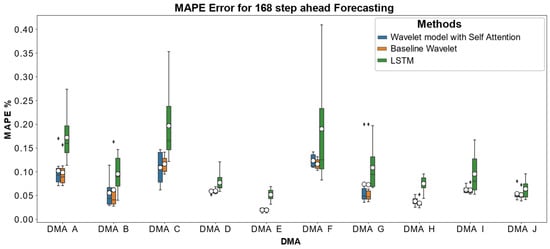
Figure 2.
Quantitative evaluation of variants of wavelet-based DL models with a baseline LSTM to measure forecasting performance in terms of MAPE.
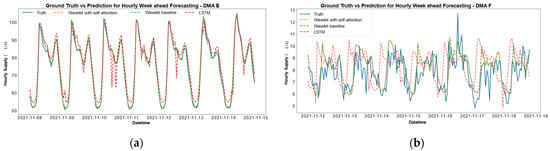
Figure 3.
Qualitative evaluation of forecasting performance for different DMAs: (a) DMA E with a MAPE of 1.9%; (b) DMA F with a MAPE of 11.6%.
4. Discussion
Through examination of Figure 2 and Figure 3, it is apparent that the forecasting proficiency of the model for predicting demand varies among different DMAs. Notably, a pronounced contrast in forecasting accuracy is observed across the models deployed for DMAs serving residential consumers within urban and rural areas. The MAPE metric for consumers in the countryside exhibited a broader variation, ranging from 3% to 11% (DMAs A, B, and C), whereas for DMAs E and G, which cater to consumers located near the city center, the error fluctuated between 2% and 4%. A nominal forecasting performance of error of less than 10% was observed for most DMAs, except for DMA F, characterized by an error of 11%. The model effectively captured the diurnal demand fluctuations during morning and evening periods but faced challenges in accurately modeling demand variations throughout the daytime, as depicted in Figure 3b. While there is no significant disparity between the wavelet models with and without attention, the attention-based model demonstrated faster convergence and training compared to the standard model. Both models significantly outperformed the baseline LSTM model.
5. Conclusions
The effectiveness of employing DL models utilizing time-frequency representation of consumption data for water demand forecasting is assessed using real-world consumption data with diverse characteristics. The DL model demonstrates its capability to produce consistent predictions across all DMAs, exhibiting minimal variance. Urban areas and industrial zones, characterized by strong periodic patterns in their time series data, are modeled more effectively than agricultural and rural zones. In the latter, the model accurately captures the pronounced diurnal pattern but struggles to capture variations throughout the day. To enhance forecasting accuracy, future research could explore techniques such as using pretrained models on similar datasets, ensemble modeling, or adopting multi-task learning approaches to leverage similarities across DMAs.
Author Contributions
Conceptualization, A.R. and S.B.; methodology, A.R.; validation, A.R.; formal analysis, A.R.; investigation, A.R.; resources, A.M. and S.B.; data curation, A.R. and H.M.; writing—original draft preparation, A.R.; writing—review and editing, A.R., A.M. and S.B.; visualization, A.R.; supervision, A.M. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bayerisches Verbundforschungsprogramm (BayVFP) des Freistaates Bayern, grant number DIK0325/01 and the APC was funded by Bayerisches Verbundforschungsprogramm (BayVFP) des Freistaates Bayern.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used for this study were made available as part of the WDSA/CCWI 2024 Conference—https://wdsa-ccwi2024.it/battle-of-water-networks/, accessed on 1 December 2023.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cosgrove, W.J.; Loucks, D.P. Water Management: Current and Future Challenges and Research Directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef]
- Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A.; Herrera, M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability 2022, 14, 5412. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-Series Forecasting with Deep Learning: A Survey. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Shen, Y.; Zhu, Y.; Yao, J. Forecasting Wavelet Transformed Time Series with Attentive Neural Networks. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; IEEE: Singapore, 2018; pp. 1452–1457. [Google Scholar] [CrossRef]
- Chatterjee, S.; Ramachandran, A.; Neergaard, T.F.; Maier, A.K.; Bayer, S. Heat Demand Forecasting with Multi-Resolutional Representation of Heterogeneous Temporal Ensemble. In Proceedings of the NeurIPS 2022 Workshop on Tackling Climate Change with Machine Learning, New Orleans, LA, USA, 9 December 2022; Available online: https://www.climatechange.ai/papers/neurips2022/46 (accessed on 2 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).