Performance Evaluation of a Specialized Pressure Sensor for Pick and Place Operations ^†

Abstract

A piezoresistive electrical bagging material with minimal cost and profile, such as linqstat or velostat, is a good choice for pressure-sensing systems in robotic arm grippers. This paper’s main objective is to examine the performance of a unique velostat-based pressure sensor system for supplying real-time grasping pressure profiles during the lifting of calibrated weights. Copper conductive tape was used to build the sensor, and it was positioned on top of and beneath a velostat sheet to serve as an electrode. The accuracy, repeatability, and hysteresis responses of the pressure sensor system were examined through a variety of experiments, as well as through testing with calibrated weights ranging from 100 gm to 2000 gm in steps. The sensor’s hysteresis and nonlinear characteristics were discovered through the experimental results of loading cycle measurements. Velostat proved to be a realistic option as a sensitive material for sensors with a single electrode pair, depending on the sensor’s sensitivity, hysteresis, reaction time, loading conditions, and deformation. The area where the velostat sensor might be implemented was verified by experimental results.

1. Introduction

In research using the haptic approach and robotics applications utilizing wearable technology, force distribution sensors and contact pressure sensors are frequently used. As a result, it is crucial to thoroughly research the design and characterization of these sensors in order to produce accurate results. Three distinct physical phenomena occurring in various materials—the piezoresistive effect, the piezoelectric effect, and variable capacitance—provide the three most popular approaches to designing electronic sensors for measuring force and pressure [1,2,3]. In numerous sorts of sensing applications, the three phenomena have been thoroughly researched. However, among these three categories of physical phenomenon, piezoresistive materials enable better metrical pressure distribution monitoring in biomedical applications given their affordability and deterministic behavior [4].

The electrical resistance of piezoresistive materials varies in response to deformation caused by an applied force [5,6] and has an inversely proportional relationship [7]. When no force is applied, the material’s electrical resistance is somewhere between megaohms and kiloohms or less [8]. In this, a paper piezoresistive sensor was tested in response to load, hysteresis, and temporal drift tests.

2. Materials and Methods

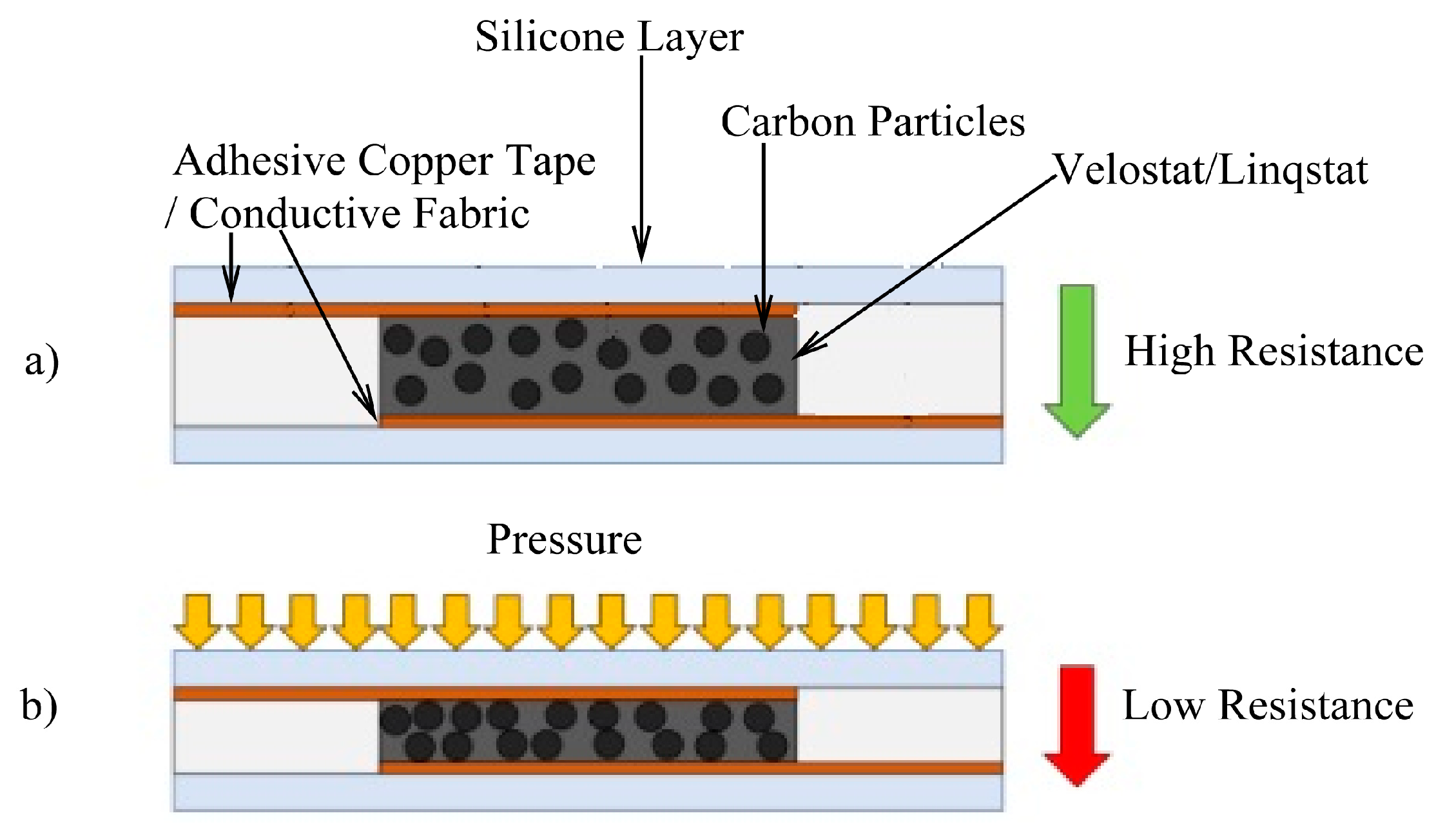
2.1. Sensor Fabrication

The materials needed for sensor fabrication are a velostat sheet, adhesive copper tape, silver conductive fabric, a silicone foam layer, etc. The velostat sheet is sandwiched in between two pieces of copper conductive tape, and then, silver conductive fabric is also placed, covering the copper conductive tape as shown in Figure 1 and Figure 2. Experimental setup for the entire system is shown in Figure 3. Over the conductive tape, a layer of silicone foam is placed so that applied pressure or force is uniformly distributed over the entire surface area of the sensor strip [9,10] The piezoresistive velostat core of the sensor has a length of 5 mm, and a thickness of 0.06 mm. The main goal of the sensor design is to reduce the size and cost of this customized sensor. Velostat is the core material of the sensor; it has a length of 105 mm, a breadth of 65 mm, and a thickness of 0.06 mm. Given the micro-Brownian motion of the carbon filler particles in the polymer, the material’s resistance decreases as force is applied to it [11,12]. Electron microscopy diagram of velostat paper is shown in Figure 4 showing the molecular structure of carbon material used.

2.2. Design Parameters of Conditioning Circuit

Equation (1) accurately shows the resistance–force relation for velostat [15].

$$R=\frac{\rho \times k}{F}$$

(1)

R: resistance of piezoresistive material;

K: surface roughness factor/coefficient;

ρ: resistivity of the contacting surfaces;

F: force applied normal to the contact surfaces.

The effect of the change in force is inversely proportional to the resistance of the sensor; moreover, k has a direct impact on the force applied while holding an object. If the value of the surface is rougher, the resistance will be greater, and the force required to lift an object will be lesser. As shown in Figure 3, a voltage divider circuit was used to transform the resistance of the sensors into a voltage signal by connecting them in series with a fixed resistor, R (10 KΩ). Applying Ohm’s law, as illustrated in Equation (2), yields the voltage read at the sensor–resistor junction.

$$V_O=V_{in} \left[\frac{\rho \times k}{F\times R_L+\rho \times k}\right]$$

(2)

R_L: voltage divider circuit’s resistance;

V_in: sensor’s input voltage;

V_o: voltage divider’s output voltage.

By taking into account Equations (1) and (2), the voltage force relationship is established. A linear response might be obtained by connecting the sensor resistor between a voltage source and the current input of a voltage converter (a virtual ground), obtaining a voltage output proportional to the piezoresistive sensor’s resistance [15].

2.3. Experimental Design Parameters [8,9,10]

The experiments focused on sensor response characteristics for distinct load levels, continuous cyclical loads, drift characteristics, and variation due to loading rate changes.

2.3.1. Hysteresis

The greatest output variation between loading and unloading a single load was referred to as hysteresis.

$$Hysterisis=\frac{\left|V_{Load}-V_{Unload}\right|}{\left|V_{Max}-V_{Min}\right|}\times 100\%$$

(3)

where V_Load and V_Unload are the sensor voltages corresponding to the greatest difference between the loading and unloading responses, and V_Max and V_Min are the sensor voltages at maximum and minimum loads, respectively [16]. Loading test with calibrated weights is shown in Figure 5.

2.3.2. Drift

Drift is described as a shift in sensor output over time for a specific load, typically an increase in value. With weights kept for five minutes, the sensor was loaded from 200 gm to 2000 gm in steps, and the variations in resistance and pressure values were noted.

2.3.3. Repeatability

The variation in output produced when a sensor is loaded to the same pressure is known as repeatability. Each sensor was loaded with a calibrated weight ranging from 100 gm to 2000 gm.

2.3.4. Effect of Temperature

The sensors were heated using a hot plate or hair dryer from room temperature up to 60 °C in steps of 5 degrees. At these temperatures, the sensor response was recorded for roughly 30 min with no loads and loads ranging from 200 gm to 2000 gm [11,12]. The temperature test is shown in Figure 6.

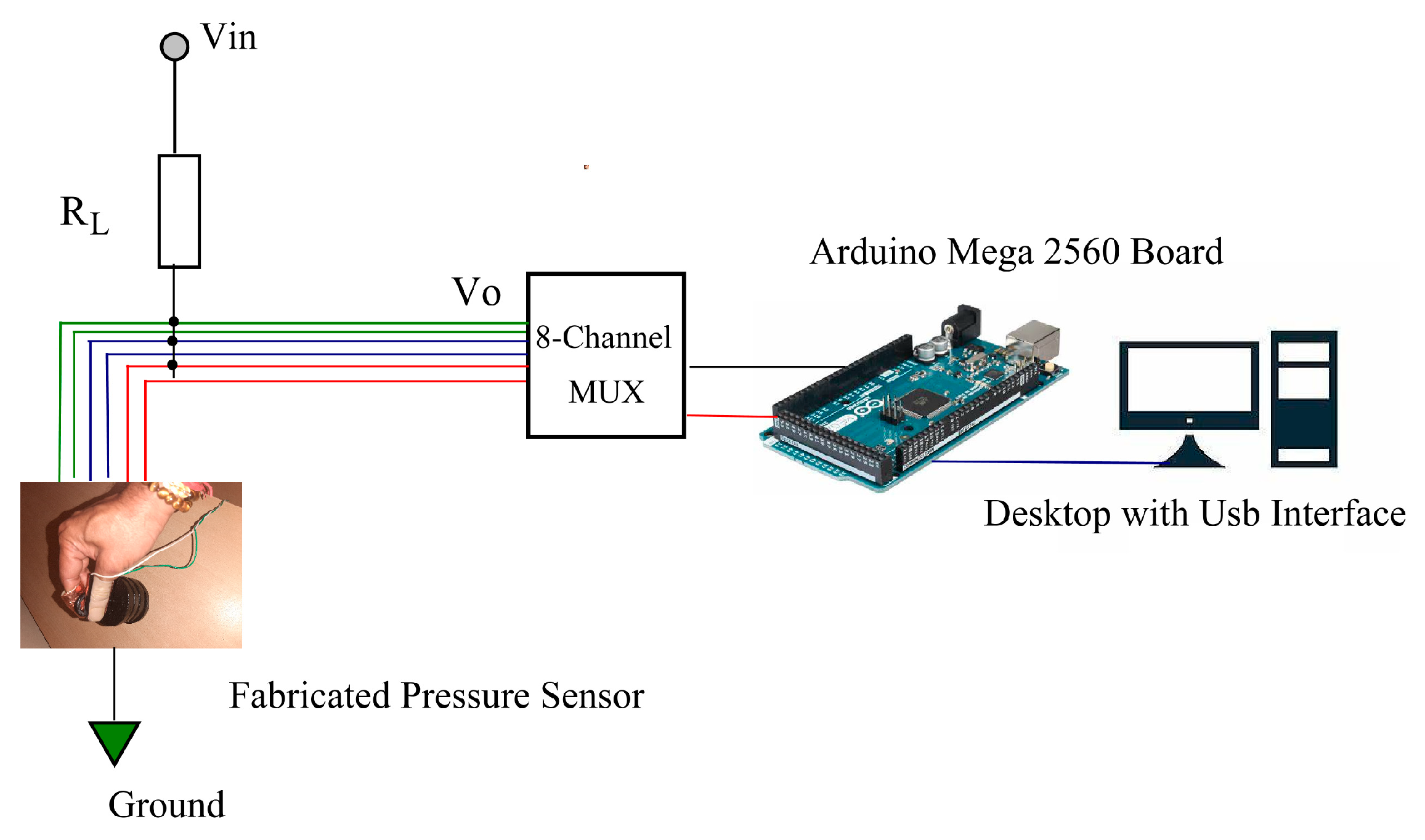
2.4. Experimental Methods

2.4.1. Pre-Commissioning Test

The fabricated sensor has to undergo various pre-commissioning tests, which include the twisting effect, bending effect, and stretching effect as in Figure 7.

2.4.2. Pre- and Post-Commissioning Tests

The results are shown in

Table 1. Variation in velostat resistance (clockwise).

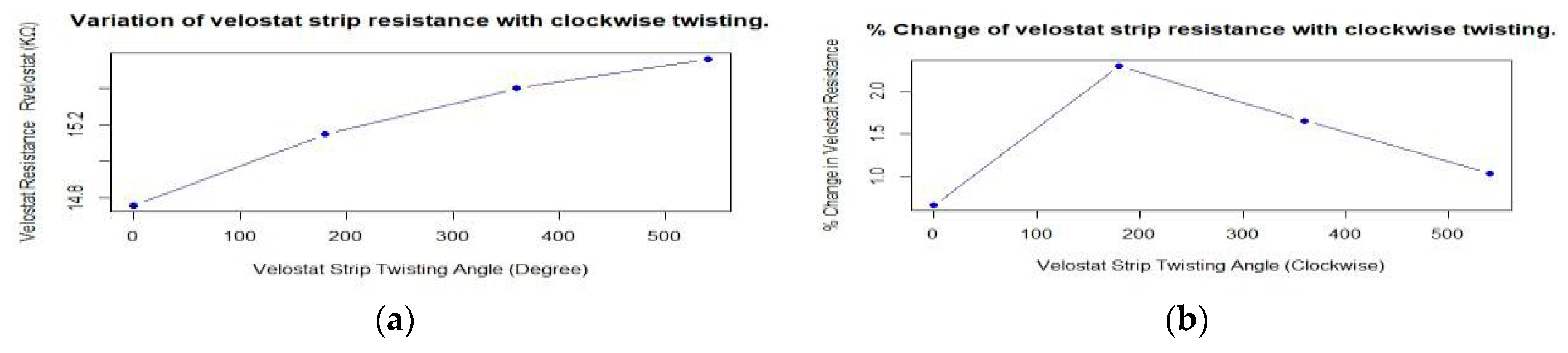
S. No	Twisting Angle in Degree(Clockwise)	Rvelostat (KΩ)	% Change in Resistance (ΔRvelostat/Rvelostat) × 100%
1	0° Twist (Flat Surface)	14.70–14.81	0.673%
2	180° Twist	15.15	2.292%
3	360° Twist	15.40	1.655%
4	540° Twist	15.56	1.039%

,

Table 2. Variation in velostat resistance (anti-clockwise).

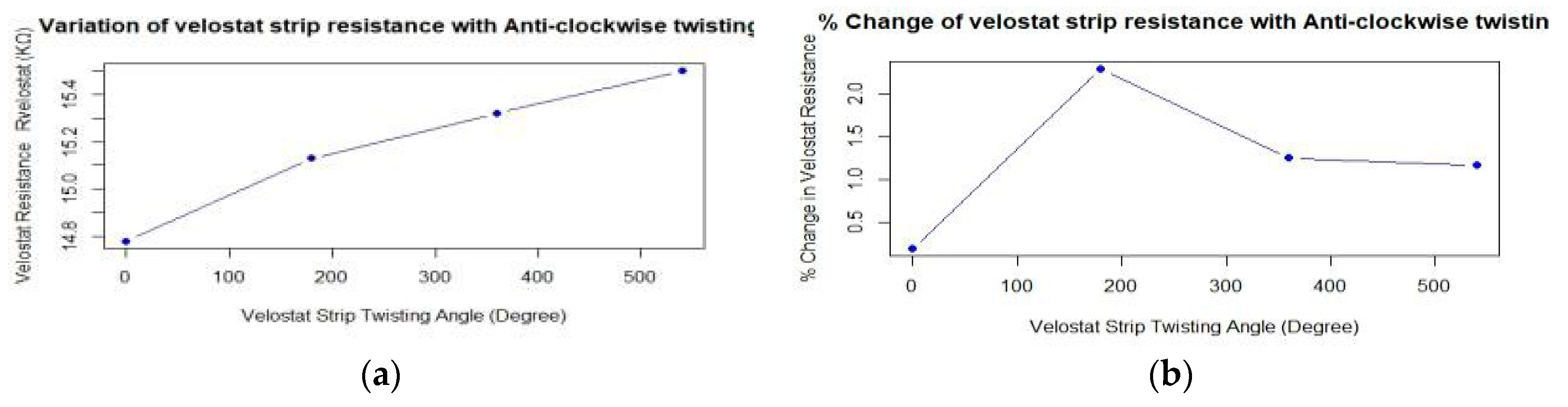
S. No	Twisting Angle in Degree (Anti-Clockwise)	Rvelostat (KΩ)	% Change in Resistance (ΔRvelostat/Rvelostat) × 100%
1	0° Twist (Flat Surface)	14.77–14.80	0.673%
2	180° Twist	15.13	2.292%
3	360° Twist	15.32	1.655%
4	540° Twist	15.50	1.039%

,

Table 3. Bending test on velostat strip.

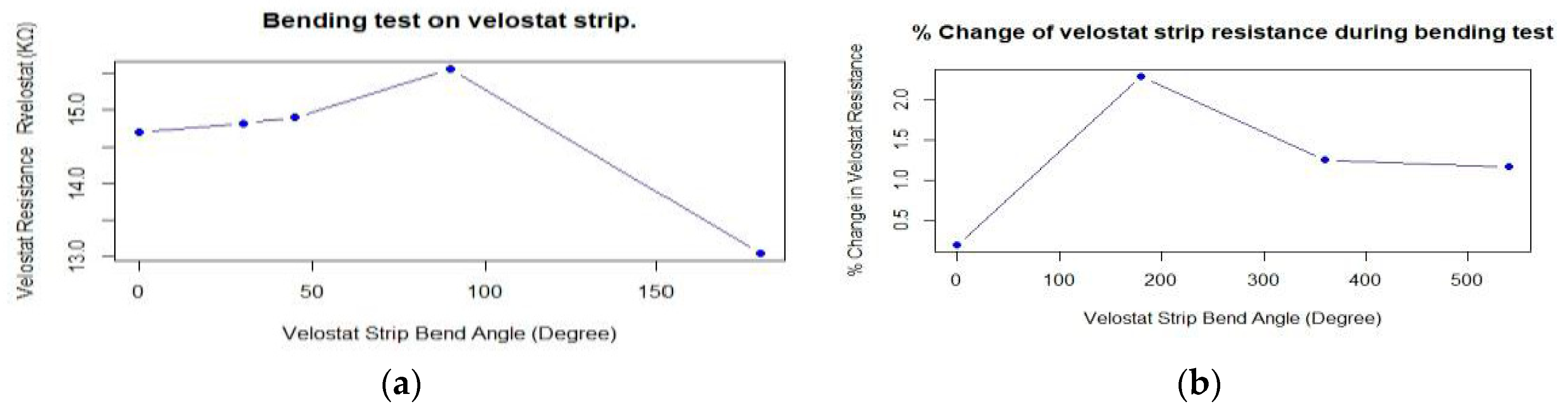
S. No	Bend Angle (Degree)	Rvelostat (KΩ)	% Change in Velostat Resistance (ΔRvelostat/Rvelostat) × 100%
1	0° (Flat Surface)	14.70	0.673%
2	30° (Light Bend)	14.82	2.297%
3	45° (Moderate bend)	14.90	1.256%
4	90° (Omega Bend)	15.56	1.173%
5	Pinch Bend	13.05	−16.124%

,

Table 4. Stretching test on velostat strip.

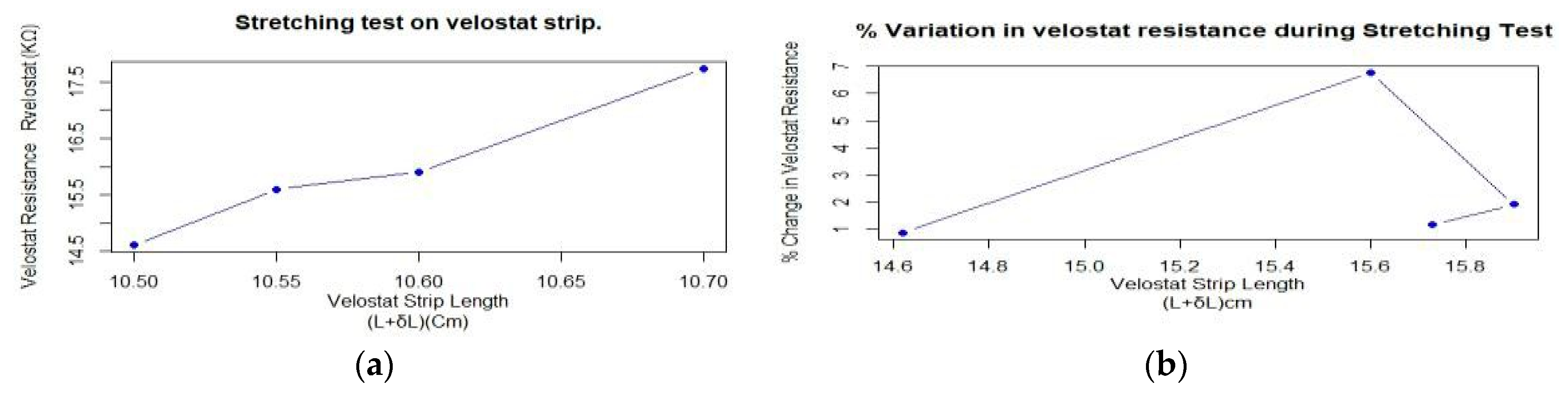
S. No	Velostat Strip Length (L + δL) cm	Rvelostat (KΩ)	% Change in Velostat Resistance (ΔRvelostat/Rvelostat) × 100
1	No Stretch (10.5)	14.55–14.68	0.855%
2	Light Stretch (10.55)	15.60	6.768%
3	Med. Stretch (10.6)	15.90	1.923%
4	High Stretch (10.7)	15.73	1.173%
5	Pinch Bend	13.05	−16.124%

,

Table 5. Loading test on the sensor (ascending weights) [18].

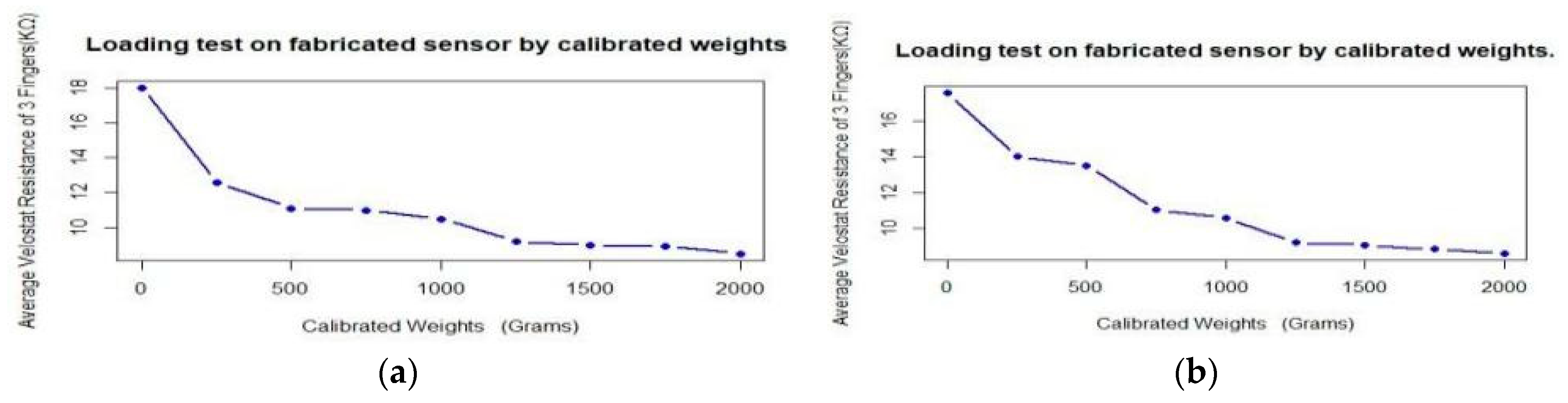
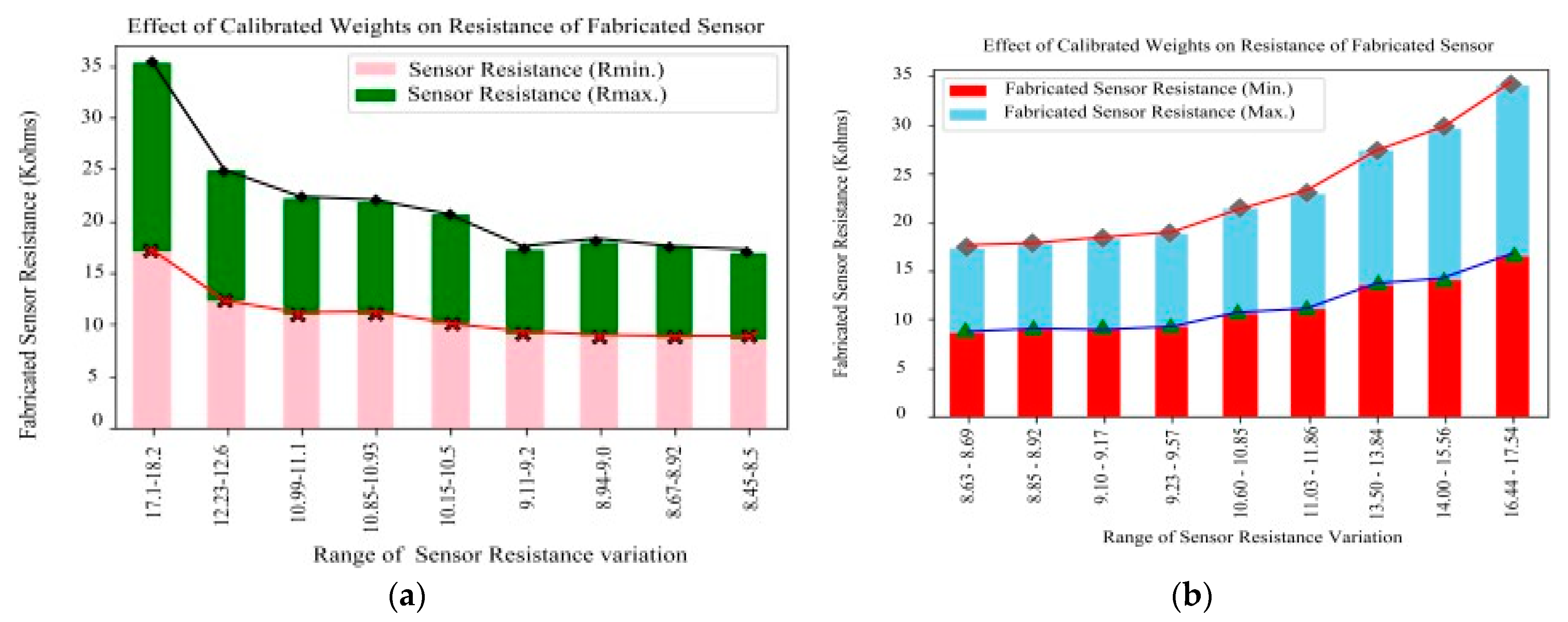
S. No	Calibrated Weights (Grams)	Resistance Range Rvelostat (KΩ)	% Change in Resistance (ΔRvelostat/Rvelostat) × 100
1	0	17.1–18.2	−30%
2	250	12.23–12.60	−11.90%
3	500	10.99–11.10	−0.09%
4	750	10.85–10.93	−4.55%
5	1000	10.15–10.50	−12.38%
6	1250	9.11–9.20	−2.17%
7	1500	8.94–9.00	−0.89%
8	1750	8.67–8.92	−4.71%
9	2000	8.45–8.50	0%

,

Table 6. Loading test on the sensor (descending weights).

S. No	Calibrated Weights (Grams)	Resistance Range Rvelostat (KΩ)	% Change in Resistance (ΔRvelostat/Rvelostat) × 100
1	2000	8.63–8.69	0%
2	1750	8.85–8.92	2.55%
3	1500	9.10–9.17	2.83%
4	1250	9.23–9.57	1.43%
5	1000	10.60–10.85	14.84%
6	750	11.03–11.86	4.06%
7	500	13.50–13.84	22.40%
8	250	14.00–15.56	3.70%
9	0	16.44–17.54	25.29%

,

Table 7. Effect of temperature on velostat material.

S. No	Ambience Temperature in Degree Celsius	Rvelostat (KΩ)	% Change in Resistance (ΔRvelostat/Rvelostat) × 100
1	24.44 (Room Temp.)	13.1	0%
2	27	14.2	8.40%
3	32	14.7	3.52%
4	37	15.3	3.92%
5	42	18.7	22.22%
6	47	21.9	17.10%
7	52	26.1	19.18%
8	57	20.4	−21.83%
9	62	18.5	−9.31%

and

Table 8. Hysteresis and drift tests on the sensor with calibrated weights.

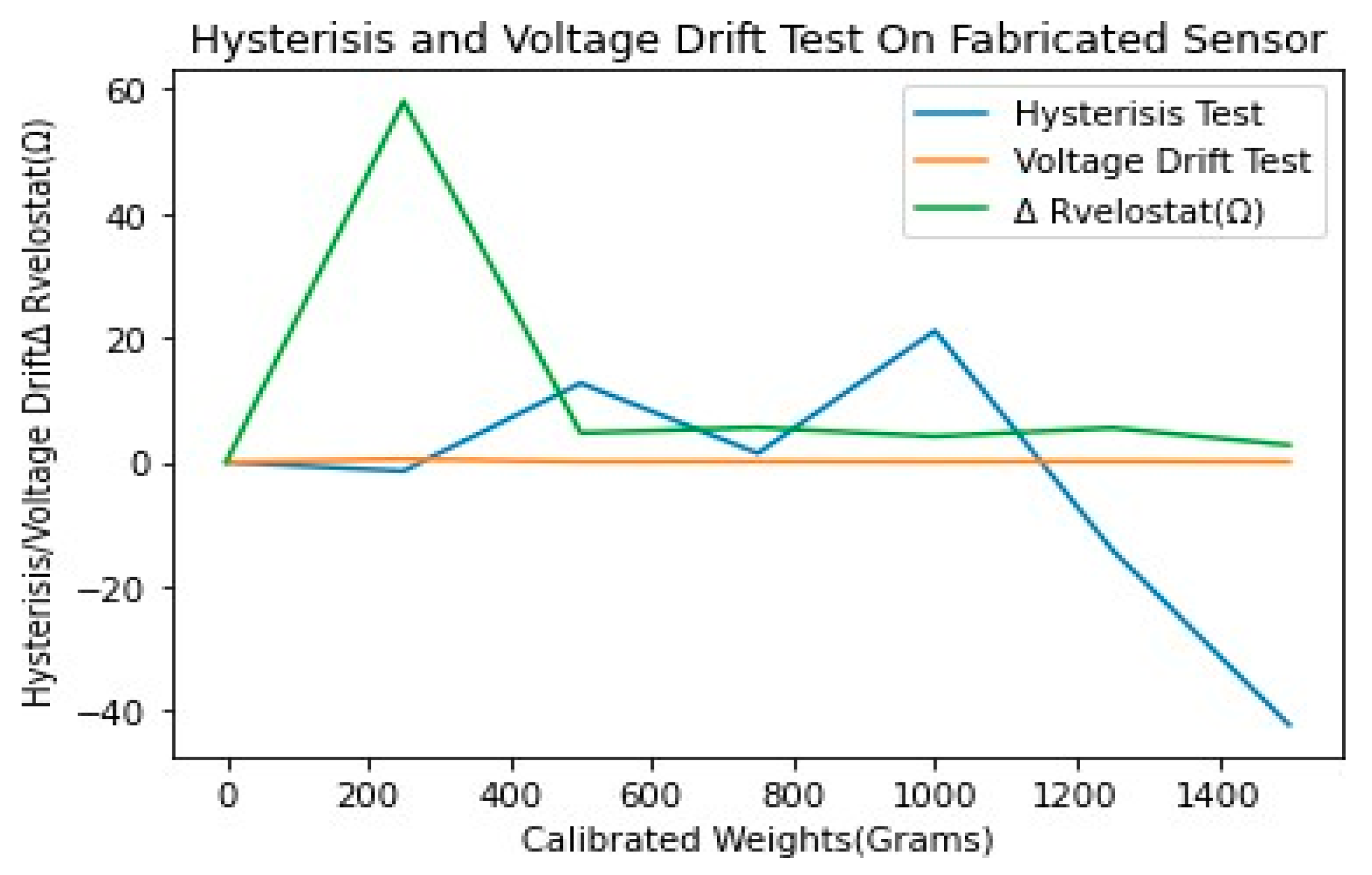
S. No	Calibrated Weights (Grams)	Hysteresis	Voltage Drift
			ΔV0	ΔRvelostat(Ω)
1	0	0%	0	0
2	250	−1.408451%	0.47	58002.11
3	500	12.67606%	0.09	4705.14
4	750	1.408451%	0.12	5565.36
5	1000	21.121761%	0.08	4154.8
6	1250	−14.08451%	0.14	5512.6
7	1500	−42.25352%	0.06	2733.62

and their related curves are shown in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

Calculations

For a calibrated weight of 1000 grams:

Drift in voltage = 1.10 – 1.02 = 0.08 V

Drift in fabricated sensor resistance = 39420.29 − 35245.29 = 4154.80 Ω

$$Hysterisis=\frac{\left|1.10-0.95\right|}{\left|1.50-0.79\right|}\times 100 \%=21.121761\%$$

For calibrated weight of 250 grams, drift in voltage = 0.91 − 0.44 = 0.47 V

Drift in fabricated sensor resistance = 102417 − 44414.89 = 58002.11 Ω

$$Hysterisis=\frac{\left|0.42-0.79\right|}{\left|1.50-0.79\right|}\times 100\%=-1.408451\%$$

3. Results and Discussion

In the fabricated sensor, hysteresis errors were observed in a range of 21.121% to –42.253% for ascending and descending weights, as shown in Figure 13a,b, Figure 14a,b and Figure 15 and observations shown in Table 8.

The sensor sensitivity changes swiftly when exceeding a load of 1000 gm, as variations in resistance are significant; therefore, a range of readings are taken and then found optimal values shown in Figure 15a,b.

The voltage drift is also quantized in the sensor, ranging from 0.06 V to 0.47 V, as shown in Table 8. The effectiveness of the sensor is greatly affected when temperature increases above 60 °C, as shown in Table 7. After 55 °C, the resistance of the sensor drops significantly, as shown in Figure 12a The significance of this sensor fabrication is that it provides sensing solutions spanning consumer, industrial, and biomedical applications, as many different engineering principles and physics phenomena are employed to sense pressure.

The advantage of using velostat as a pressure-sensing element is that it is low cost, low power consumption, and has simple electronic circuitry. The limitations include its high sensitivity to pressure variations since output from the sensor is temperature-dependent, and problems with coating material and adhesives at temperatures beyond the sensor’s permissible values. Hysteresis can also affect performance matrices like accuracy, stability, precision, etc.

4. Conclusions

It is evident from the above observations and performance curves that the proposed specialized pressure sensor works satisfactorily during pick-and-place operation with calibrated weights and can safely be deployed with robotic arm grippers to grasp objects.