Abstract
Picking an appropriate parameter setting (meta-parameters) for visualization and embedding techniques is a tedious task. However, especially when studying the latent representation generated by an autoencoder for unsupervised data analysis, it is also an indispensable one. Here we present a procedure using a cross-correlative take on the meta-parameters. This ansatz allows us to deduce meaningful meta-parameter limits using OPTICS, DBSCAN, UMAP, t-SNE, and k-MEANS. We can perform first steps of a meaningful visual analysis in the unsupervised case using a vanilla autoencoder on the MNIST and DeepVALVE data sets.
1. Introduction
High-dimensional data creates the need for simplification, of which low-dimensional embeddings as well as data visualization constitute two closely related methodologies. Their goal is to preserve the main patterns within the data and obtain a less complex data representation, which for two or three-dimensional embeddings grants also direct visual access on the data. It is well known that finding a low-dimensional data embedding is a meticulous, parameter- and data dependent task for which optimization may be difficult [1]. However, in our approach, we take into account that even the visualization space for an appropriate embedding is related to a set of visualization parameters, which we call meta-parameters.These are not directly optimized over, but introduce bias in the visualization itself when chosen poorly. One example the reader might know is the fact that DBSCAN suffers from the curse of dimensionality, when the minimal number of neighboring points is chosen unfortunately [2,3]. For our investigation, we chose the challenging setting of data (namely MNIST [4] and DeepVALVE [5]) compressed within the latency space of an autoencoder.
1.1. Why Are Autoencoders Interesting?
The idea of autoencoders exists for more than 30 years [6] and the applications are presently widespread. They range from generalization to classification tasks, denoising, anomaly detection, recommender systems, clustering and dimensionality reduction with stunning results [7,8,9,10,11,12,13]. Within this work, we focus on the latter two use cases, wherein autoencoders perform unsupervised feature extraction and dimensionality reduction [14,15]. Autoencoders consist of an encoder-decoder structure as explained in Figure 1.
Figure 1.
Architecture of an autoencoder. The left side constitutes the encoder while the mirror image around the middle is called decoder. The exact composition of the layer structure is given in Appendix A.
To achieve their above-mentioned goal, the data is embedded within a latency space via the encoder. Usually, the latent dimension is much smaller than the one of the original data set. This kind of setting is also known as bottleneck architecture. From this embedding, the original data representation is reconstructed by the decoder. The system is trained by minimizing the reconstruction error. Conceptually, autoencoders can be seen as a nonlinear generalization of PCA [16]. Under postulation of the manifold hypothesis [17], in some settings, they are supposed to learn the intrinsic low-dimensional data manifold embedded (nonlinearly) into the high-dimensional data observation space. Even more, in this vein they can be interpreted as a nonlinear embedding approach on their own. In the context of unlabeled high-dimensional data sets and especially time series, autoencoders have shown to be powerful tools for unsupervised analysis tasks [15,18]. Yet it has become clear in several applications that the “classical” loss term might not be enough to capture the desired behavior [19]. For this reason, some researchers try to ameliorate the reliability and efficiency of their autoencoder models by introducing additional, task dependent loss-terms (e.g., Ref. [20] introduced a topological loss term to preserve connected components within the data; Ref. [21] introduced a perceptual loss to improve image classification; Ref. [22] introduced a loss term to fix class centroids within a classification task).
1.2. Our Approach
In this work, we approach this problem upside down. We develop methods to investigate the autoencoder’s capability to conform to the manifold hypothesis in a visual and qualitative way, which integrates into the general trend of visualization methods gaining more importance over the last while [23,24,25]. Our goal is to give data scientists a non-mathematical and interpretable tool at hand to monitor and supervise the nonlinear embedding process whose result constitutes the latency space. To do so, we proceed as follows: First, we must formulate our concepts. To make clear what is new to our approach, we must distinguish it from classical parameter and hyperparameter tuning models.
Definition 1
(Parameters). Parameters are the quantities that determine the actual shape of the data manifold.
Intuitively, parameters determine the “physics” of our data under consideration. In the case of our autoencoder, they are given by the trainable weights.
Definition 2
(Hyperparameters). Hyperparameters are the quantities that determine the performance, the setup, and the training of our neural, data driven model in a metrisable way.
A summary of our autoencoder model and the corresponding hyperparameters can be found in Table A1 and Table A2 in Appendix A. The decoder is just a mirror in our case. (Although sometimes a weight tie is implemented too, we adhere from this technique here).
Definition 3
(Meta-parameters). Meta-parameters are the quantities that determine the performance of our neural, data driven model in a non-metrisable way.
So, it becomes clear why standard (hyper-)parameter optimization methods cannot be applied to the present purpose: Lacking a metric, there is now quantifiable (stochastic) optimization procedure to find an optimal embedding. For this reason, we took a step back on to a qualitative level and performed a cross-correlative study including t-SNE, UMAP, k-MEANS, DBSCAN and OPTICS.
1.3. Embedding and Visualization Methods
The use of visualization methods to analyze structures of interest for a higher-dimensional space by a visual inspection of a lower-dimensional embedding has become a popular approach in recent years, compare [26,27,28,29,30,31,32,33,34,35]. Usually, embedding schemes are classified and distinguished based on their embedding properties, e.g., to discriminate linear and nonlinear embeddings. Thus, to cover an appropriate set of embedding techniques for reasons of comparison, our approach covers a comparative study of different embedding techniques. In the following, a short description of these methods is given. Table A3 in Appendix B states the meta-parameters and their default values.
1.3.1. t-SNE
The t-SNE algorithm assigns mutual “neighborhood”-probabilities based on a distance metric (most commonly the Euclidean one) between points, and successively tries to minimize the Kullback–Leibler divergence. The most important hyperparameter is the perplexity, which defines the minimum number of neighborhood points. However, the hyperparameters of the intrinsic optimization algorithm also have crucial impact on the final 2- or 3-dimensional embedding [36,37].
1.3.2. UMAP
This algorithm represents an advancement with respect to t-SNE by constructing a “fuzzy simplicial complex” on the data. However, choosing the appropriate radius for the related Cěch complex is a meticulous task. Additionally, the choice of the metric and the minimum number of neighboring points determine the resulting 2- or 3-dimensional embedding. Like t-SNE, UMAP’s dependence on the metrified minimum point distance makes it prone to the curse of dimensionality [38].
1.3.3. k-MEANS
K-Means minimizes the metric distance of data points to predefined cluster centers. This also constitutes its major drawback, aside from not being able to identify noise and imposing complexity on all cluster shapes [39].
1.3.4. DBSCAN
Unlike k-MEANS, DBSCAN is a density-based method able to identify noise and clusters of all shapes. Its main hyperparameters are , the critical value for which points are seen to belong to the same cluster, and , the minimum number of points that shall belong to one cluster. As is chosen globally, DBSCAN has its difficulties with clustering heterogeneous data [40].
1.3.5. OPTICS
OPTICS has many commonalities with DBSCAN. The most substantial difference to DBSCAN is that is chosen from a dendrogrammatic graph called the reachability plot. This is based on one of its two main parameters: the reachability distance. This expresses the smallest distance for an object p with respect to another object o, such that p is directly density-reachable from o if o is a core object. Intuitively, a core object is one that lies in the vicinity of . The reachability plot depicts the reachability distances for each object in the cluster ordering. Clusters within the data set are regions where the reachability distance between points are small, so they correspond to “valleys” within the reachability plot. The reachability plot is rather insensitive to and , but if is too small, then too many points will have an undefined reachability distance. In contrast to DBSCAN, OPTICS has difficulties when clustering homogeneous data [41].
1.4. Organization and Contribution of the Paper
The main part of our work is given by Section 2, where we elaborate on the nature of our cross-correlative approach before demonstrating how our iterative and interactive cross-study systematically leads to more stable meta-parameter settings on MNIST in Section 2.1. Secondly, we apply our procedure to the DeepVALVE time series data in Section 2.2. In Section 3 we study the visualizations generated by the found meta-parameters. Finally, in Section 4, we conclude on the range of visualization meta-parameters and their connection to unsupervised learning. The contributions of this work are
- autoencoder study on DeepVALVE data set
- cross-correlative study of embedding technologies
- procedure to gain manageable meta-parameter ranges
- visual analysis of autoencoder latency spaces
2. Cross-Correlative Study on Meta-Parameters
For our comparative meta study of dimension reduction algorithms, we define the meta-parameters to be
where is the space of values the individual meta-parameters may take, see Table A3. A meta-parameter set of a concrete visualization might be a k-dimensional vector embedded into a k-dimensional meta-parameter space. To elucidate this, considering multi-parameter visualization such as the radial visualization method introduced by [42], one faces a (meta-) parameter space k with parameters , n being the number of data dimensions. Finding a good meta-parameter combination introduces generally an NP-hard issue to optimize the meta-parameters in k-dimensions (within the single algorithm regime). Thus, our working hypothesis states insight can be gained about by cross-studying from a multi-algorithmic point of view:
where denotes the set of algorithms and denotes the -th meta-parameter of algorithm . Doing so saves the trouble of solving the (k-dimensional) meta-parameter problem for one specific algorithm. Instead, we iter- and interactively tune mutually to approach a valuable embedding and visual representation for the data in touch. Let be the range for the cardinality of cluster centers with respect to one of the methodologies as quoted above. Then our evaluation results in a cross-correlative range matrix
Herein, denotes the intersection of the range of cluster center cardinalities for two methods :
By definition, the matrix in Equation (3) is symmetric around the diagonal. The goal is now to find the minimum of the to come as close to the true intrinsic dimension of the data manifold as possible.
2.1. MNIST
The MNIST data set is a well-known image data set containing the digitalization of around 60,000 handwritten digits from zero to nine. Many studies performed with this data set may be found in the literature [43,44]. Therefore, we omit any additional details of this data set except the fact that it is labeled, i.e., for each picture we know which digit is actually depicted. We start our analysis with the reachability plot for the OPTICS algorithm. For computational reasons we fix to 3.5, see Appendix C.1.
As shown on the right-hand side of Figure 2, no meaningful structures can be found for as all points are qualified as noise, which refines the order of magnitude mentioned in [41] for meaningful . The general features of the reachability plot itself are known to be stable under some (meaningful) variations of the meta-parameters and [41]. Valleys in this plot, as shown on the left-hand side of Figure 2, may be connected to clustered structures in the studied latency space as explained in Section 1.3. Tuning , i.e., the red dashed line in Figure 2, we can identify at least six independent structures at the same resolution scale. We also show other, rather poorly tuned values for , i.e., , indicated by the black dashed lines.
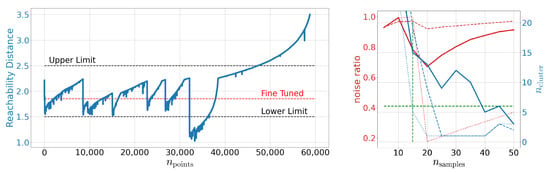
Figure 2.
Left: Reachability plot for the OPTICS algorithm on MNIST. This plot is produced using and . Right: The number of identified noise points as well as the number of found clusters as function of for OPTICS. We display different selections with indicated by the dashed, solid, and dotted line, respectively. The green dashed lines indicate the limits deduced so far.
To bolster this observation, we study the embeddings as computed by t-SNE and UMAP in Figure 3. By eye we can see that both methods give a different perspective on the structure of the latent space. Using t-SNE alone we might identify between six and eleven structurally independent components. On the other hand, UMAP would provide us with six or maybe seven independent structures. Especially the derived upper bounds are very subjective. How should the gaps actually look to be counted as independent? At this point we see how the cross-correlative nature of our approach adds value. By now we have clearly established a lower limit of six cluster structures using Figure 2 (left) and Figure 3 (left and middle). In addition, we have limited . At the right-hand side of Figure 2, we show the number of identified clusters as well as the noise ratio for OPTICS as a function of for different values of . We observe that it actually is the fine-tuned run which yields the best signal-to-noise ratio while simultaneously respecting the derived lower limits on . Indicating the so far deduced boundaries by green dashed lines we can set an upper limit on the number of identified clusters. Again, we have settled for rather conservative boundaries by working with . Using the best signal-to-noise ratio, both from Figure 2 and Figure 3, yields and thus an upper bound of 13 clusters instead of 18. Using this knowledge, let us study the next embedding tool on our list: DBSCAN. As OPTICS and DBSCAN are closely related we can use the already identified values of and as starting points. This greatly reduces the meta-parameter space to be explored. Indeed, as we can see in Figure 3, DBSCAN favors slightly higher and lower values of than OPTICS. However, as OPTICS requires values for and high enough to not fall into the unstable regime, one should also choose for DBSCAN not too low. This ”unstable” behavior can be observed also in Figure 3 for values of . Hence we transfer the OPTICS limit to DBSCAN here and arrive at a fine-tuned limit of 11 clusters. So, in total we find

Figure 3.
Left and Middle: Structure of the latent space distribution of MNIST as identified by the t-SNE respectively UMAP embedding. Right: (blue) and noise ratio (red) as a function of with (dashdot), (dashed), (solid), and (dotted) for DBSCAN. The green dashed lines indicate the limits deduced so far.
Again, we emphasize that wherever necessary we use very conservative heuristics. Therefore, the suggested limits in Equation (5) capture the full structure of the latent representation as produced by our autoencoder.
2.2. DeepVALVE
The DeepVALVE data set consists of a series (in total around 25,000) of random opening and closing events of an industrial valve as described in [5]. A part of these events is shown in Figure 4.
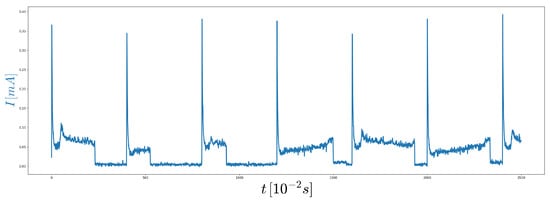
Figure 4.
Part of the DeepVALVE time series data set: The blue line represents the measured electrical current driving the engine of the valve.
The allowed labels are: START, LOSE, LINEAR, STUCK, END. Thus, as in the case of MNIST, we have a completely labeled data set where we know the cluster cardinality beforehand, see Appendix D for more examples. As we deal with a time series data set, we must specify the way we feed our data to the neural network. Denoting our time series with , we extract windows at time step t of window size w, i.e., . A batch is then created by randomly sampling t. As in this case our latent space is three-dimensional, we are actually able to plot it. The found structure for is shown in Figure 5. We observe an ellipsoidal structure which is typical for quasi-periodic structures, as indicated in [45]. This is not surprising regarding the recurring opening and closing events of the valve. Now we want to apply the investigative pipeline we developed in Section 2.1. Hence again we start with the OPTICS reachability plot in Figure 6. We can identify several bigger and smaller structures. The reachability graph yields at least three or even four and more structures.
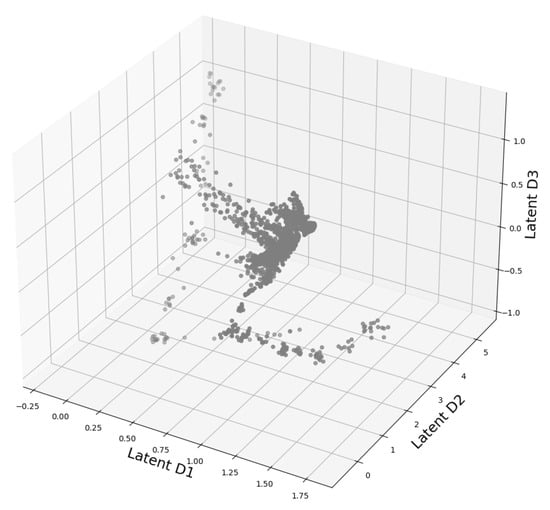
Figure 5.
3D presentation of the latent space of DeepVALVE dataset as computed by our autoencoder.
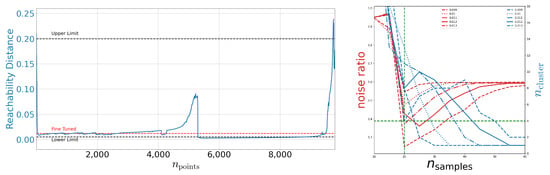
Figure 6.
Left: Reachability plot for the OPTICS algorithm on DeepVALVE. This plot is produced using and . Right: Noise ratio and number of found cluster as deduced from the OPTICS reachability plot as a function of with .
Adding the knowledge of Figure 7 we can estimate the lower limit of identified structures as four. Following Section 2.1 one can estimate from the signal-to-noise ratio on the right-hand side of Figure 6. Again, we fine-tune using the reachability graph. We identify using this optical procedure. On the right-hand side of Figure 6 we show runs with different fine-tuned values. Indeed, the visual tuning turns out to be not sensitive enough and the actual range for epsilon is rather in the range of 0.01. We use this figure to estimate the upper limit of identified clusters to be 13.

Figure 7.
Left and Middle: Structure of the latent space distribution of DeepVALVE as identified by the t-SNE respectively UMAP embedding. Right: The number of identified noise points as well as the number of found clusters as function of for DBSCAN. We display different selections with indicated by the dashed, dotted and solid line, respectively. The green dashed lines indicate the limits deduced so far.
In Figure 7 one can observe the (within the context of temporal data emerging) fact that outliers can be detected with UMAP more easily than with t-SNE [46,47]. In addition to that, UMAP also preserves global structures better than t-SNE, although there are more advanced methods such as dynamic t-SNE including a notion of temporal coherence that allows for better cluster separation [48]. Summing up, from the t-SNE plot, in view of cluster sizes and distances with no specific meaning, one can identify (conservatively estimated) 7 clusters. However, the UMAP plot in the middle of Figure 7 indicates around 5 clusters. Using the limits deduced so far we study DBSCAN on the right-hand side of Figure 7. As with MNIST we observe that DBSCAN prefers slightly different values for . So, in total we find
3. Visualization of Clustered Data
In Section 2 we estimated the meta-parameters of our benchmark data set MNIST and our testing case DeepVALVE within Equations (5) and (6) respectively. However, how does this help us to gain a better visual understanding of the data set under investigation? Using our set of meta-parameters, we can now study the t-SNE and UMAP embeddings for our OPTICS, DBSCAN and k-MEANS clustering methods to obtain a first grasp on how well the data are classified and separated within the latent space. From Equation (5) we chose settings as disclosed in Table 1.

In Figure 8 we show the clusters found by OPTICS, DBSCAN, and k-MEANS projected onto the t-SNE embedding. We observe that both OPTICS and DBSCAN exhibit oversimplification as has already been visible in Figure 3. Additional structures are only indicated, as few points have been assigned to them. K-MEANS, however, though able to resolve much more substructure, tends also to split certain structures which the other methods clearly identified as belonging together. The reason is that the predefiniton of cluster cardinalities introduces some bias. We observe a similar behavior when using the UMAP embedding in Figure 9 instead. This provides us with the possibility of a direct comparison between t-SNE and UMAP embeddings, which is not possible a priori.

Figure 8.
T-SNE embedding of the latent space of our MNIST autoencoder. In color the points belonging to identified cluster structures. From left to right: OPTICS, DBSCAN, k-MEANS.

Figure 9.
UMAP embedding of the latent space of our MNIST autoencoder. In color the points belonging to identified cluster structures. From left to right: OPTICS, DBSCAN, k-MEANS.
Let us now apply the same procedure to our test data set DeepVALVE. Again, using the values from Table 1 we project the found clusters onto the t-SNE, respectively the UMAP embeddings. In Figure 10 and Figure 11 we can see real structural differences of the DeepVALVE dataset to the MNIST dataset, Figure 8 and Figure 9. Figure 10 (left and middle) clearly reveals that OPTICS is much more sensitive to heterogeneities within the data.
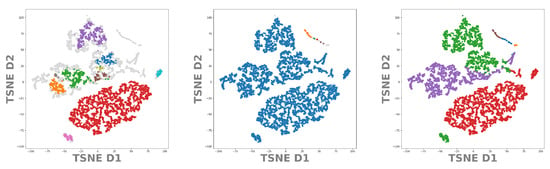
Figure 10.
T-SNE embedding of the latent space of our DeepVALVE autoencoder. In color the points belonging to identified cluster structures. From left to right: OPTICS, DBSCAN, k-MEANS.

Figure 11.
UMAP embedding of the latent space of our DeepVALVE autoencoder. In color the points belonging to identified cluster structures. From left to right: OPTICS, DBSCAN, k-MEANS.
This can be an advantage but also a disadvantage: As DeepVALVE is a huge data set with densely distributed points, density-based clustering methods—and especially OPTICS—find more clusters for smaller training sets. For DeepVALVE, We observed a huge difference between 10,000 and 60,000 points (10,000 depicted in Figure 10). The reason is that larger distributions become “filled in” the more samples are drawn from the true distribution. k-MEANS, on the other hand, constitutes a biased version of clustering, which reveals itself for the MNIST as well as for the DeepVALVE data set within the t-SNE as well as within the UMAP embedding. A comparison of Figure 10 and Figure 11 reveals the main advantage claimed for UMAP in the literature: That it can depict and preserve (global) similarities better [49]. This is even more critical for time series than for image data, as time series segmentation often exhibits not as many labels as classification tasks for image data. Hence the procedural error by choosing wrong cluster cardinalities rises significantly. Thus, our pipeline involving the cross-correlative usage of clusterings and embeddings raises awareness of this fact as well as giving a first hint onto the scale at which cluster center cardinalities can be expected.
4. Conclusions
Summing up what we have done and learned so far, we can identify four main benefits of our approach:
- (i)
- We developed a pipeline to obtain a visual grasp on the generalization capacity of a vanilla autoencoder.
- (ii)
- We use clustering and embedding methods in a cross-correlative way to fine-tune their observational capabilities.
- (iii)
- This cross-correlative ansatz allows better capture of the interrelation between the (transformed) data and the visualizations and embeddings.
- (iv)
- Doing so, structural differences between data sets become apparent, which allows obtaining a first apprehension of an unknown data set without prior knowledge.
4.1. The Generalization Capacity vs. the Manifold Hypothesis
One should keep in mind the reason for investigating the latency space in this detailed fashion: We want to have a grasp on the generalization assumption. This is connected, but not identical to the manifold hypothesis as presented in the introduction. For both of our data sets we know the cluster center cardinalities beforehand and hence we can evaluate the individual performance of our clustering algorithms on the latent space. However, if this is not the case—which it should be for unsupervised learning tasks—our cross-correlative ansatz can give a first hint.
4.2. Meta-Parameter Fine-Tuning
In Equations (5) and (6) we present the results of our (visual) meta-parameter fine-tuning. Especially Figure 2 and Figure 6 reveal how visual investigation ameliorates our results. Although these clustering and embedding methods work well within certain ranges of parameters, as e.g., Ref. [41] points out and investigates in detail for OPTICS, visual methods and their consecutive analysis can really suffer from poorly chosen meta-parameters. So, by working in a cross-correlative way one introduces a level of quantitivity that one would completely loose when restricting to one method.
4.3. Interrelation between Data and Methodology
In Figure 12 the latent space of the DeepVALVE dataset is investigated using our three different clustering methods, and one can clearly see that something goes wrong for OPTICS. So why is this the case? DeepVALVE is a dense temporal data set, and one would expect the clusters corresponding to the temporal labels to lie at the “edges” of the quasi-periodic structure depicted in Figure 12. However, unlike DBSCAN, OPTICS uses not a point value, but a hierarchical scale range for the reachability distance. Thus, if we have a really dense data set and comparatively few samples to estimate its distribution, it might identify large parts of the data set as noise. This can happen neither with DBSCAN nor k-MEANS. Henceforth, we have another demonstration that also visual methods should be taken with a grain of salt at least in the unsupervised case.
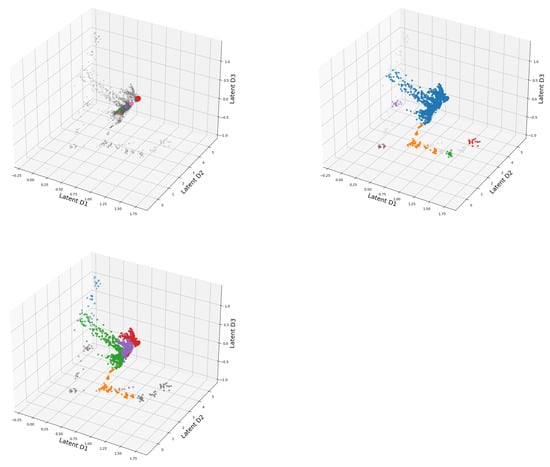
Figure 12.
3D presentation of the latent space of DeepVALVE dataset using OPTICS, DBSCAN, K-Means clustering, respectively.
4.4. Structural Differences between Data Sets
In Section 2.1 and Section 2.2 we studied two structurally different data sets with the same analysis pipeline as developed in Section 2. Although MNIST constitutes a image dataset, DeepVALVE consists of temporal measurements of a physically non-trivial process and hence exhibits more structure, as depicted in Figure 4. This is clearly visible from the clustering parameters and , indicating DeepVALVE is a much denser data set than MNIST, as well as from the respective visualizations. Especially in Figure 8 to Figure 11 this shows itself, as discussed in Section 3.
4.5. Future Outlook and Comparison to Other Work
In [46] a deep convolutional autoencoder was used as a dimensionality reduction method for the subsequent visualization using PCA, UMAP and t-SNE. They too developed a pipeline for a quantitative investigation; however, in contrast to our work, they did not use the visualization and embedding methods in a cross-correlative way. As our results indicate, e.g., in Figure 2 and Figure 6, this adds value to the inter-correlated usage of density-based clustering methods. For future investigation, we plan to migrate our visual meta-parameter selection pipeline (partly) to the hyperparameter learning level. Especially the qualitative analyses in Figure 2 and Figure 6 would profit from a deeper, quantitative treatment. Furthermore, we would like to investigate the conjunction between the cardinality of training samples necessary to obtain a “good” estimate on the data distribution and data density in a more sophisticated manner. Especially temporal data sets are prone to heterogeneities that even have physical meaning rather than just being clustering or embedding artefacts. Having performed this comprehensive study, we are keen to walk one step further on this road.
Data Availability Statement
MNIST is available from http://yann.lecun.com/exdb/mnist/. DeepValve is a company-internal IAV dataset. It will be published in an anonymised fashion following this publication.
Appendix A. Autoencoder Hyperparameters and Architecture for Reproducibility
In Table A1 our choices for the autoencoder hyperparameters are listed. Please note that if not mentioned otherwise, the default values of PyTorch (Version 1.8.1) are used.

Table A1.
The hyperparameters used for training our model.
Table A1.
The hyperparameters used for training our model.
| Hyperparameter | Values |
|---|---|
| Learning Rate | |
| Optimizer | Adam |
| Random Seed | 0 |
| Activation Function of hidden layers | ReLU |
| Activation Function of output layer | Sigmoid |
| Epochs | 100 |
| Batch Size | 100 |
| Loss | Mean Square Error |
Table A2 summarizes the encoder-decoder structure of the autoencoder as well as the final validation loss.

Table A2.
Architecture of the encoder chosen for the given data set and achieved validation loss. The architecture numbers represent the number of neurons per layer.
Table A2.
Architecture of the encoder chosen for the given data set and achieved validation loss. The architecture numbers represent the number of neurons per layer.
| Data Set | Input Size | Architecture | |
|---|---|---|---|
| MNIST | 784 | ||
| DeepVALVE | 10 |
Please note that the decoder is a mirror of the encoder. Therefore, we omitted the numbers in Table A2.
Appendix B. Meta-Parameter Default Values

Table A3.
List of meta-parameters used in this study.
Table A3.
List of meta-parameters used in this study.
| Embedding Method | Meta-Parameters Used and Their Default Values |
|---|---|
| t-SNE | , |
| UMAP | , |
| DBSCAN | , |
| OPTICS | , |
| K-Means | , , |
| , , , | |
Appendix C. Additional Material for MNIST
Appendix C.1. Reachability Plots
In Figure A1 we show additional plots using different values for and .
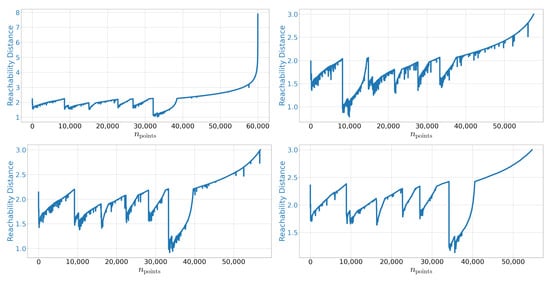
Figure A1.
OPTICS reachability plot for MNIST using. Left upper: and . Right upper: and . Left lower: and . Right lower: and .
As stated in [41] the key features of this plot are rather stable against different choices of the meta-parameters.
Appendix C.2. Reconstructed Digits
For MNIST we can qualitatively check the identified structures. For all three clustering approaches we construct a cluster center. For k-MEANS this is done automatically by the algorithm. On the other hand, for OPTICS and DBSCAN we just use the center of mass of all points belonging to a given cluster. We then reconstruct the images by sending these points through the decoder.
In Figure A2 we present the reconstructions corresponding to the right-hand side of Figure 8, respectively Figure 9 in the main text. We observe that indeed most of the digits could be identified. However, digit 4 is missing, while digit 1 and 9 are doubled. A behavior we already observed in Section 2.1.

Figure A2.
Reconstructed images of the centroids of the cluster using K-Means clustering with .
Once we increase the allowed number of clusters to , as shown in Figure A3, we observe that now all digits are present. However, we also have quite some doubling in digits 0 to 4.

Figure A3.
Reconstructed images of the centroids of the cluster using K-Means clustering with .
As displayed in Figure A4 a similar behavior emerges when we use DBSCAN instead. Using the values from Table 1 we recover most digits except 8 and 9. Again for the other digits we have several clusters they belong to.

Figure A4.
Reconstructed images of the centroids of the cluster using DBSCAN clustering with and .
Finally in Figure A5 we show the reconstructed digits for OPTICS. Again, we observe missing digits, 3 and 5 this time, as well as two versions of 4.

Figure A5.
Reconstructed images of the centroids of the cluster using OPITCS clustering with and .
Interestingly, k-MEANS has trouble locating different digits when compared to OPTICS and DBSCAN. The latter two behave rather similar again.
Appendix D. Additional Material for DeepVALVE
In Figure A6 we show additional labeled data samples from [5].
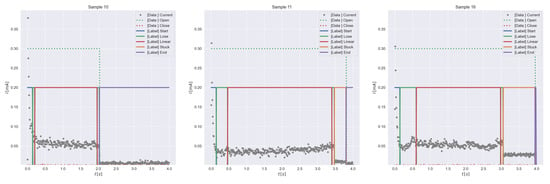
Figure A6.
Additional labeled data samples for DeepVALVE.
References
- Donoho, D.L. High-dimensional data analysis: The curses and blessings of dimensionality. In Proceedings of the AMS Conference on Math Challenges of the 21st Century, Los Angeles, CA, USA, 7–12 August 2000. [Google Scholar]
- Sembiring, R.W.; Mohamad Zain, J.; Abdullah, E. Dimension Reduction of Health Data Clustering. arXiv 2011, arXiv:1110.3569. [Google Scholar]
- Chen, Y.; Tang, S.; Bouguila, N.; Wang, C.; Du, J.; Li, H. A Fast Clustering Algorithm based on pruning unnecessary distance computations in DBSCAN for High-Dimensional Data. Pattern Recognit. 2018, 83. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Ahmed, S.; Schichtel, P.; von der Ohe, T. Sensorlose Prozesse mit kuenstlicher Intelligenz erfassen und steuern. MTZextra 2018, 23, 42–45. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Parallel Distributed Processing. Volume 1: Foundations; MIT Press: Cambridge, UK, 1986. [Google Scholar]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2021, arXiv:2003.05991. [Google Scholar]
- Rossler, A.; Cozzolino, D.; Verdoliva, L.; Riess, C.; Thies, J.; Niessner, M. FaceForensics++: Learning to Detect Manipulated Facial Images. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Zhang, Y.; Lee, K.; Lee, H. Augmenting Supervised Neural Networks with Unsupervised Objectives for Large-scale Image Classification. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 612–621. [Google Scholar]
- Zhang, B.; Qian, J. Autoencoder-based unsupervised clustering and hashing. Appl. Intell. 2021, 51, 493–505. [Google Scholar] [CrossRef]
- Li, X.; Zhang, T.; Zhao, X.; Yi, Z. Guided autoencoder for dimensionality reduction of pedestrian features. Appl. Intell. 2020, 50, 4557–4567. [Google Scholar] [CrossRef]
- Ferreira, D.; Silva, S.; Abelha, A.; Machado, J. Recommendation System Using Autoencoders. Appl. Sci. 2020, 10, 5510. [Google Scholar] [CrossRef]
- Takeishi, N.; Kalousis, A. Physics-Integrated Variational Autoencoders for Robust and Interpretable Generative Modeling. arXiv 2021, arXiv:2102.13156. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 7 May 2021).
- Lee, W.; Ortiz, J.; Ko, B.; Lee, R.B. Time Series Segmentation through Automatic Feature Learning. arXiv 2018, arXiv:1801.05394. [Google Scholar]
- Dunteman, G.H. Principal Component Analysis; SAGE Publications: Thousand Oaks, CA, USA, 1989. [Google Scholar]
- Fefferman, C.; Mitter, S.; Narayanan, H. Testing the Manifold Hypothesis. arXiv 2013, arXiv:1310.0425v2. [Google Scholar] [CrossRef]
- Ryck, T.D.; Vos, M.D.; Bertrand, A. Change Point Detection in Time Series Data using Autoencoders with a Time-Invariant Representation. arXiv 2021, arXiv:2008.09524. [Google Scholar]
- Lapuschkin, S.; Wäldchen, S.; Binder, A.; Montavon, G.; Samek, W.; Müller, K.R. Unmasking Clever Hans Predictors and Assessing What Machines Really Learn. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Moor, M.; Horn, M.; Rieck, B.; Borgwardt, K.M. Topological Autoencoders. arXiv 2019, arXiv:1906.00722. [Google Scholar]
- Pihlgren, G.G.; Sandin, F.; Liwicki, M. Improving Image Autoencoder Embeddings with Perceptual Loss. arXiv 2020, arXiv:2001.03444. [Google Scholar]
- Zhu, Q.; Zhang, R. A Classification Supervised Auto-Encoder Based on Predefined Evenly-Distributed Class Centroids. arXiv 2020, arXiv:1902.00220. [Google Scholar]
- Chel, S.; Gare, S.; Giri, L. Detection of Specific Templates in Calcium Spiking in HeLa Cells Using Hierarchical DBSCAN: Clustering and Visualization of CellDrug Interaction at Multiple Doses. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 2425–2428. [Google Scholar] [CrossRef]
- Cai, T.T.; Ma, R. Theoretical Foundations of t-SNE for Visualizing High-Dimensional Clustered Data. arXiv 2021, arXiv:2105.07536. [Google Scholar]
- Swetha, S.; Kuehne, H.; Rawat, Y.S.; Shah, M. Unsupervised Discriminative Embedding for Sub-Action Learning in Complex Activities. arXiv 2021, arXiv:2105.00067. [Google Scholar]
- Lehmann, D.J.; Theisel, H. Orthographic Star Coordinates. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2615–2624. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, A.; Soguero-Ruiz, C.; Mora-Jimenez, I.; Rivas-Flores, F.J.; Lehmann, D.J.; Rubio-Sánchez, M. Scaled radial axes for interactive visual feature selection: A case study for analyzing chronic conditions. Expert Syst. Appl. 2018, 100, 182–196. Available online: https://www.sciencedirect.com/science/article/pii/S0957417418300617 (accessed on 12 May 2021). [CrossRef]
- Rubio-Sánchez, M.; Sanchez, A.; Lehmann, D.J. Adaptable Radial Axes Plots for Improved Multivariate Data Visualization. Comput. Graph. Forum 2017, 36, 389–399. [Google Scholar] [CrossRef]
- Shao, L.; Mahajan, A.; Schreck, T.; Lehmann, D.J. Interactive Regression Lens for Exploring Scatter Plots. Comput. Graph. Forum 2017, 36, 157–166. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Nie, F.; Theisel, H.; Gong, M.; Lehmann, D.J. Linear Discriminative Star Coordinates for Exploring Class and Cluster Separation of High Dimensional Data. Comput. Graph. Forum 2017, 36, 401–410. [Google Scholar] [CrossRef]
- Lehmann, D.J.; Theisel, H. The LloydRelaxer: An Approach to Minimize Scaling Effects for Multivariate Projections. IEEE Trans. Vis. Comput. Graph. 2017. [Google Scholar] [CrossRef]
- Lehmann, D.J.; Theisel, H. General Projective Maps for Multidimensional Data Projection. Comput. Graph. Forum 2016, 35, 443–453. [Google Scholar] [CrossRef]
- Lehmann, D.J.; Theisel, H. Optimal Sets of Projections of High-Dimensional Data. IEEE Trans. Vis. Comput. Graph. 2015. [Google Scholar] [CrossRef]
- Karer, B.; Hagen, H.; Lehmann, D. Insight Beyond Numbers: The Impact of Qualitative Factors on Visual Data Analysis. IEEE Trans. Vis. Comput. Graph. 2020. [Google Scholar] [CrossRef]
- Rubio-Sánchez, M.; Lehmann, D.; Sanchez, A.; Rojo Álvarez, J. Optimal Axes for Data Value Estimation in Star Coordinates and Radial Axes Plots. Comput. Graph. Forum 2021, 40. [Google Scholar] [CrossRef]
- Pezzotti, N.; Lelieveldt, B.; van der Maaten, L.; Höllt, T.; Eisemann, E.; Vilanova, A. Approximated and User Steerable tSNE for Progressive Visual Analytics. IEEE Trans. Vis. Comput. Graph. 2016, 23, 1739–1752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hinton, G.; Roweis, S. Stochastic Neighbor Embedding. Neural Inf. Process. Syst. 2002, 857–864. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. Proc. Berkeley Symp. Math. Stat. Probab. 1967, 1, 281–297. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; Simoudis, E., Han, J., Fayyad, U.M., Eds.; KDD; AAAI Press: Palo Alto, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; peter Kriegel, H.; Sander, J. OPTICS: Ordering Points To Identify the Clustering Structure; ACM Press: New York, NY, USA, 1999; pp. 49–60. [Google Scholar]
- Hoffman, P.; Grinstein, G.; Marx, K.; Grosse, I.; Stanley, E. DNA visual and analytic data mining. In Proceedings of the Visualization ’97 (Cat. No. 97CB36155), Phoenix, AZ, USA, 19–24 October 1997; pp. 437–441. [Google Scholar] [CrossRef]
- Shamsuddin, M.R.; Rahman, S.; Mohamed, A. Exploratory Analysis of MNIST Handwritten Digit for Machine Learning Modelling. In Proceedings of the 4th International Conference on Soft Computing in Data Science, SCDS 2018, Bangkok, Thailand, 15–16 August 2018; Springer: Singapore, 2019; pp. 134–145. [Google Scholar] [CrossRef]
- Schott, L.; Rauber, J.; Brendel, W.; Bethge, M. Robust Perception through Analysis by Synthesis. arXiv 2018, arXiv:1805.09190. [Google Scholar]
- Tralie, C.J.; Perea, J.A. (Quasi)Periodicity Quantification in Video Data, Using Topology. arXiv 2017, arXiv:1704.08382. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.; Jones, M.W.; Xie, X. TimeCluster: Dimension reduction applied to temporal data for visual analytics. Vis. Comput. 2019, 35, 1013–1026. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.; Alqahtani, A.; Jones, M.W.; Xie, X. Clustering and Classification for Time Series Data in Visual Analytics: A Survey. IEEE Access 2019, 7, 181314–181338. [Google Scholar] [CrossRef]
- Rauber, P.E.; Falcão, A.X.; Telea, A.C. Visualizing Time-Dependent Data Using Dynamic t-SNE; Bertini, E., Elmqvist, N., Wischgoll, T., Eds.; EuroVis 2016—Short Papers; The Eurographics Association: Aire-la-Ville, Switzerland, 2016. [Google Scholar] [CrossRef]
- Vernier, E.F.; Garcia, R.; da Silva, I.P.; Comba, J.L.D.; Telea, A.C. Quantitative Evaluation of Time-Dependent Multidimensional Projection Techniques. arXiv 2020, arXiv:2002.07481. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).